交流电机绕组的气隙磁势与电势计算
谢宝昌
(上海交通大学电子信息与电气工程学院,上海 200240)
交流电机绕组的气隙磁势和电势计算是“电机学”课程中交流电机的基本内容,是研究和分析异步电机和同步电机的理论基础。两者计算方法既具有相似性又具有差异性,既要紧紧围绕交流绕组的排列和连接规律,又要灵活分析抓住本质。只有让学生对交流绕组排列规律、三相对称电流与气隙旋转磁场表达形式有清晰认识,才能很好地理解气隙磁势与气隙磁场的关系。学生应该明白计算气隙磁势的重要性,理解气隙磁势和绕组相电势计算的方法,同时明确各相绕组空间轴线(相轴)的位置,电势与产生电势的磁场相位关系。我们在计算中引入的短距、分布和绕组系数的含义,逐步建立起用等效三相整距集中绕组作为单元电机分析交流电机的理论依据。
本文推导了三相交流绕组磁势时空函数和相电势瞬时值表达式,弥补了“电机学”教材分析中将幅值与空间或时间相位分离的不足[1,2]。
1 三相对称绕组的实现
三相对称绕组不仅空间排列要对称,而且通过连接方式实现正弦旋转磁场下的电压、电流和电势在时间上也是对称的,即满足图1的对称耦合关系。

图1 对称性耦合关系
为简化分析,我们假设每个线圈结构和匝数相同且空间均匀分布;每极每相槽数为整数;气隙均匀且很小,忽略气隙磁场径向不均匀性;铁芯相对磁导率无穷大,槽内导体集中在槽口中心位置。
电枢铁芯冲片均匀分布齿槽。设第一个槽中心空间电角为零,编号为k的槽空间电角表示为

其中,槽间电角α=2πp/Z,极对数p和槽数Z。
线圈空间电角等于线圈有效边所在槽空间电角平均值,那么线圈轴线电角 γk=(θk+θk+y)/2,其中线圈两有效边之间的节距为y槽。
用槽空间电角和节距系数β=2py/Z表示为
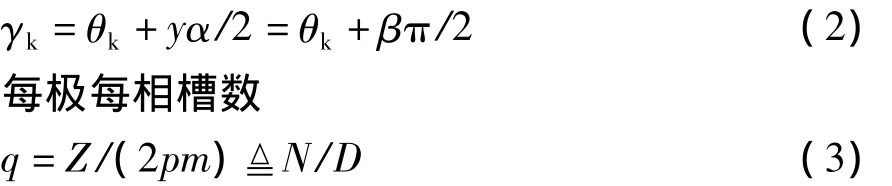
槽分配要对称,分母D不能为相数m的倍数。对称绕组的槽分配原则是将N尽可能均匀的分为D等分所获得的循环序列。例如三相四极15槽电枢,q=5/4,槽分配循环序列是2111。
本文讨论整数槽双层绕组,D=1,连续q=N个槽分配给一相带的上层边,下层边由线圈节距确定。三相对称绕组上层边槽号k分配规律如下:

线圈连接规律是每极下各相带内线圈依次串联构成极相组,相邻磁极同相极相组线圈可以反相并联或串联,但每条并联支路上的线圈数必须相同。
2 气隙磁势计算
三相对称绕组气隙磁势由三相对称电流产生,各相电流为时间正弦波且三相对称,统一表示为
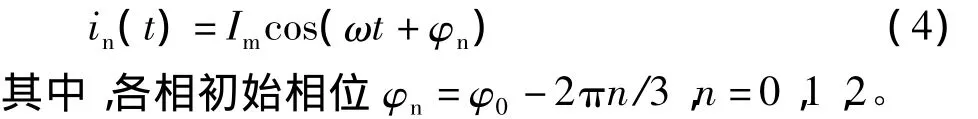
现在,我们定义气隙磁势为气隙磁场由转子到定子磁位降:

其中,气隙处转子半径为Rr,定子电枢半径为Ra。
由上式可知,计算气隙磁势空间分布间接地获得了气隙磁场空间分布。为此引入与线圈相关联的波形函数,它是以2pπ电角为周期的函数,线圈有效边所在位置发生单位阶跃突变,一个周期内正负半波面积相同,如图2所示。

图2 波形函数
波形函数表示1匝线圈1A电流产生的气隙磁势,该空间对称的周期函数经过傅立叶分解得到
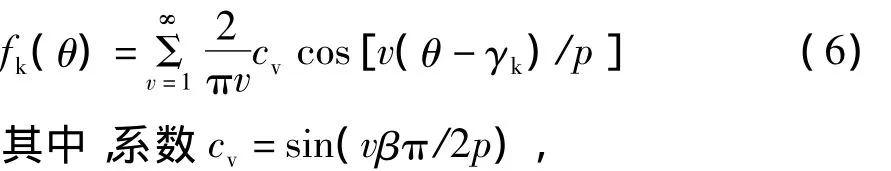
根据上式具有Nk匝且电流为ik(t)的线圈产生的磁势空间分布表示为
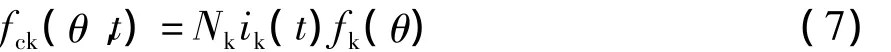
它是时间和空间变量分离的波形,时间和空间都具有周期性。根据上式得到三相双层对称交流绕组气隙磁势空间分布为
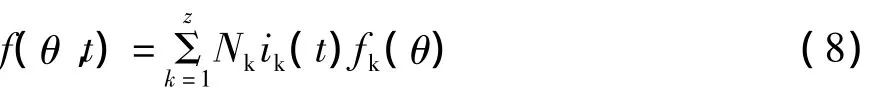
整数槽绕组每相每极q个连续线圈串联构成极相组,因此极相组内线圈电流相同,但同相相邻两个极相组电流相反;不同相绕组电流对称,60°相带绕组极相组空间依次按照AZBXCY排列,三相磁势可以按照不同相,不同极相组和不同磁极分别求和计算,设极距 τ=Z/2p,令K=2nq+1+l+kτ,则上式转化为

其中,a为每相绕组的并联支路数。
设交流绕组每相串联匝数W=2pqNc/a,则将式(10)和式(11)代入式(9)得到

将式(12)空间变量用复数表示,并考虑到上式中变量n,l和k是可以通过复指数乘积分离的,交换求和次序,得到一相绕组磁势表示形式:

其中,A相绕组相轴位置 θ=γ1+(q-1)α/2,绕组系数kwv=kyvkqv,短距系数kyv=sin(vβπ/2),分布系数kqv=sin(vqα/2)/qsin(vα/2)。
上式说明每极每相一个线圈产生的气隙磁势是以2电角度为周期的奇数次正弦波之和,不存在偶数次和分数次谐波磁势。
对于分数槽绕组,由于每相每极下线圈空间分布既不对称也不均匀,因此除了基波磁势和整数次谐波磁势,还含有分数次谐波磁势,即以2πD/p机械角为周期的自然数次磁势波各分量。
一相磁势基波幅值所在位置称为相轴,相轴位置与起始线圈空间位置关系
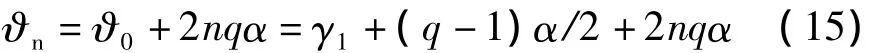
式(14)表明每相绕组产生的气隙磁势是随电流交变的所有奇数次脉振磁势波之和。将相电流式(4)化为复数形式

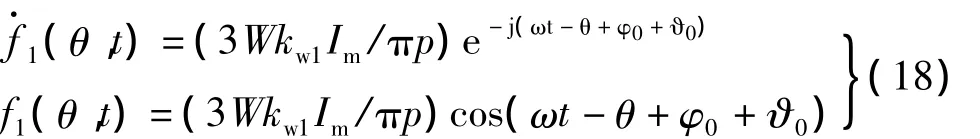
上式表明每个脉振磁势波又可以分解为两个幅值和转速相同而转向相反的旋转磁势波。三相合成正、反转磁势波的存在性取决于各相电流时间初始相位φn,绕组相轴空间相位θn和磁势波次数v值。
对于基波v=1,时间正相序,空间正相序,顺时针旋转各相旋转磁势相位互差2π/3而抵消,合成磁势逆时针以同步速旋转,由式(17)得到
上式表明三相合成基波磁势幅值所在位置总是超前A相绕组轴线位置电流时间相位角。
对于三次及其倍数次谐波v=2mN-m,时间正相序,空间同相位,正、反转磁势与合成磁势都为零。
对于v=2mN-1次谐波,时间正相序,空间反相序,逆时针旋转各相磁势相位互差2π/3而抵消,顺时针旋转各相相位相同,合成磁势为

对于v=2mN+1次谐波,时间正相序,空间正相序,顺时针旋转各相磁势互差2π/3而抵消,逆时针旋转各相磁势同相位,合成磁势为
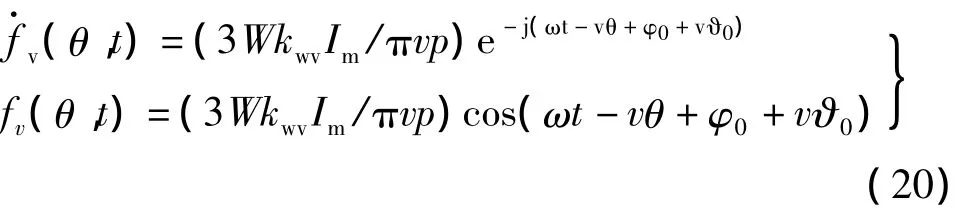
式(19)和式(20)表明v=2mN±1次谐波磁势的转速只有三相合成基波磁势转速的1/v,削弱5次和7次等低次谐波磁势是绕组设计主要考虑因素。如β=4/5可以消除5次谐波,β=5/6可以同时削弱两者。
3 相电势计算
时空正弦波旋转磁场分两类气隙磁场:磁极磁场和电枢磁场。它们产生的电势是不同的。
磁极磁场只有奇数次正弦波且空间转速相同

其中,电枢直径为Da,轴向有效长度为lfe,线圈电势与线圈边所在磁感应强度之差呈正比。
线圈空间相位转变为电势计算的时间初相位。
考虑到式(22),则上式用复数表示为
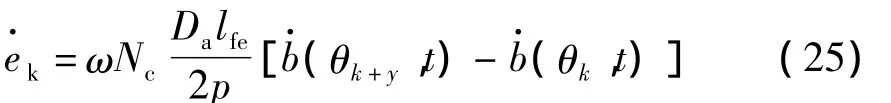
线圈电势等于槽电势之差乘以线圈匝数,滞后的时间初相位取决于槽所在磁场空间相位。
将式(2)和式(22)代入上式并化简后得

4 电势与磁势的关联性
磁势与电势计算中都出现短距、分布和绕组系数,它们将电势和磁势紧密联系在一起,本质是将三相对称短距分布整数槽绕组等效成三相集中整距绕组,具有极对数个单元电机,因此对于基波来说只要分析2π电角度三相集中整距绕组。
基波和奇数次谐波具有如下的物理意义:
(1)短距系数的物理意义是:将短距线圈等效成轴线位置不变的整距线圈引起的等效匝数之比。也等价于正弦波气隙磁场中实际线圈磁通(磁链,电势)与相同匝数整距线圈磁通(磁链,电势)之比:
(2)分布系数的物理意义是:将分布线圈等效成轴线位置不变的集中线圈引起的等效匝数之比。也等价于正弦波气隙磁场中实际分布线圈极相组磁链(电势)与总匝数和轴线相同的集中线圈磁链(电势)之比:
(3)绕组系数的物理意义是:将极相组等效成相轴位置不变的整距集中线圈引起的等效匝数之比。也等价于正弦波气隙磁场中实际一相绕组磁链(电势)与相同匝数整距集中线圈一相绕组磁链(电势)之比。
5 结语
本文从波形函数出发,给出了三相合成磁势空间分布函数的叠加表达式;然后针对三相对称整数槽绕组的线圈排列规律形成快速计算气隙磁势多重和式,并确定各相相轴位置;再利用磁极旋转磁场的特点获得线圈电势,利用绕组连接规律和空间相位引起线圈电势相位不同的求和获得绕组相电势瞬时表达式,并确定电势与磁场的相位关系,进一步得到电枢磁场引起的绕组相电势;最后对绕组系数的物理意义作了深入分析,并得到如下重要结论:
(1)一个线圈或极相组的磁势是以2π机械角或2pπ电角为周期。一个线圈的磁势波形等于波形函数与线圈匝数和电流三者乘积,包含所有自然数次数的正弦波脉振磁势,每个正弦磁势波的幅值位于线圈轴线上。
(2)每相每极一个线圈空间互差π电角组成一个集中子绕组,其磁势是以2π电角为周期,包含所有基波和奇数次数谐波的脉振正弦磁势波,每个正弦磁势波的幅值位于线圈轴线。对称整数槽绕组每相相当于存在q个集中子绕组,空间依次互差一个槽间电角α。
(3)每个正弦波脉振磁势都可以分解成幅值和转速相同而转向相反的圆形旋转磁势,旋转的电角速度等于电流角频率与正弦波次数之比。
(4)三相对称整数槽绕组磁势没有三次及其倍数次谐波,只有基波和2mN±1次谐波。基波顺相序旋转,三相基波磁势幅值等于每相基波磁势幅值的3/2倍。2mN+1次谐波与基波转向相同,2mN-1次谐波与基波转向相反,n次谐波转速应是基波的1/n。磁势幅值与谐波次数成反比,主要用短距和分布绕组消除或削弱5次和7次气隙磁势谐波。
(5)基波电流产生的电枢磁场在自身绕组中感应基波电势,同步旋转磁极谐波磁场产生谐波电势。
(6)三相磁势计算采用模为幅值且空间相位为复角的一系列复数求和,相电势计算采用模为幅值且磁场相位为复角的一系列复数求和。绕组系数的物理意义是将实际绕组等效成相轴空间位置不变的极对数个整距集中绕组单元电机引起的每极每相等效匝数变化。因此n次波对应的绕组系数也等价为n次正弦波气隙磁场在实际绕组一相磁链(电势)与等效整距绕组一相磁链(电势)之比。
[1]许实章,电机学[M],北京,机械工业出版社,1982年
[2]周顺荣,电机学[M],北京,科学出版社,2007年

