陶瓷干法造粒机的数值模拟及其优化设计

吴南星，廖达海，肖志锋

（景德镇陶瓷学院机械与电子工程学院，江西 景德镇 333403）

陶瓷干法造粒机的数值模拟及其优化设计

吴南星，廖达海，肖志锋

（景德镇陶瓷学院机械与电子工程学院，江西 景德镇 333403）

陶瓷行业干法造粒制粉取代原有的高能耗、高污染湿式球磨-喷雾造粒制粉是社会生产发展所趋。本文针对陶瓷干法造粒机颗粒充分分散性问题，采用CFD软件欧拉双流体模型建立三维数学模型。利用有限体积法求解不同主轴偏心率与筒体倾斜角的模型，模拟出颗粒的体积分布大小，同时分析颗粒的团聚现象。模拟结果表明，当偏心率为-0.3、倾斜角为150时，颗粒的分散性最佳。该模拟优化设计在一定程度上解决了干法造粒制粉颗粒的充分分散性问题，为陶瓷干法造粒机的研制具有一定的指导意义。

欧拉双流体模型；数值模拟；充分分散性；优化设计

0 引 言

目前陶瓷行业制粉主要采用的是湿式球磨-喷雾干燥工艺。该工艺技术应用于制备陶瓷墙地砖压形粉料，可以很好的满足大吨位自动压砖机的生产要求。但是，就该工艺相关统计可知，其产品的生产能耗占陶瓷生产成本的30～40%，并且排放大量的热风热气、SO2、CO2及烟尘。从而导致巨大的能源浪费和环境污染。然而，近几年来兴起的干法造粒制粉技术可以从根本上解决陶瓷行业粉体制备方面的高能耗、高污染的问题[1]。

干法造粒制粉技术在国内外陶瓷行业的发展中仍处于初步阶段，要在广大的陶瓷生产企业中得到应用， 需要解决的技术难题比较多， 核心的问题主要集中在四个方面[2-6]：一是要彻底解决好真颗粒的充分分散性问题；二是要彻底解决假颗粒的成形压缩比问题；三是要解决好坯料混色均匀及发色能力问题；四是要解决成套的、连续的生产装备供应问题。本文从有效颗粒的充分分散性问题出发，通过改变干法造粒机筒体倾斜角度及主轴偏心率，基于CFD软件分析了干法造粒机在造粒的过程中颗粒的体积分布情况和颗粒团聚现象，从而在一定程度上优化设计筒体倾斜角和主轴偏心率。

1 建模机理分析

筒体内固体颗粒体积分数较大，且初始状态颗粒的粒径为0.013 mm，故固体颗粒物料可作拟流体相处理。结合空气相，本文选用欧拉双流体模型来模拟干法造粒机造粒过程。由陶瓷粉体物料性质、造粒过程中气固两相运动特点，作如下假设：1）物料为等径球形颗粒；2）忽略造粒过程中单个颗粒的体积变化；3）系统内颗粒相与空气相共存并相互渗透，具有各自的速度和体积分数，各参数在空间中具有连续的分布，并且颗粒相和空气相分别采用质量守恒方程和动量方程求解。

1.1 多相流模型

Fluent 模拟多相流的模型主要有VOF (volume of fluid) 模型、Mixture 混合模型和欧拉模型，三种模型分别应用于不同的多相流体流动特性。本文选用欧拉模型，该模型基于分子动力学的颗粒动力学理论建立了颗粒相流体的控制方程，以颗粒的非弹性碰撞作为颗粒相能量的耗散方式，将颗粒流中颗粒的相互碰撞、摩擦以及其他能量的耗散方式都转化为相应的粘度来考虑。相可以是液体、气体、固体的几乎是任意的组合[7]，每一相都采用 Eulerian 处理。故正好吻合本文研究的气-固两相流。其控制方程如下：

1）体积分数方程：

式中：q为颗粒相， 是q相的物理密度，为q相体胀系数。

2）质量守恒方程：

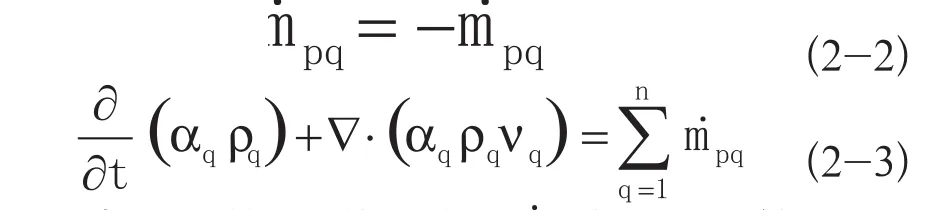
3）动量守恒方程：

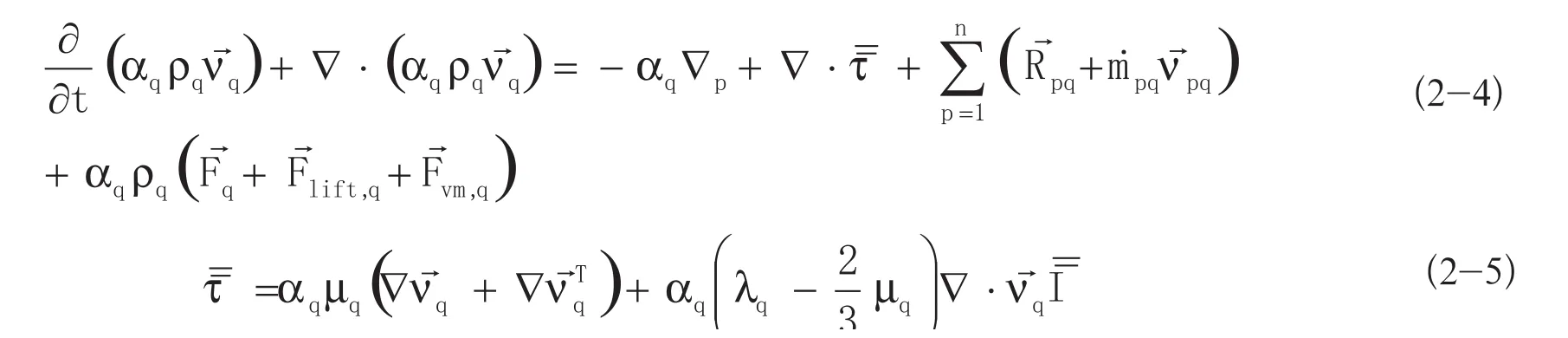
在本文模拟计算中，将空气设置为主相，颗粒设置为第二相。

1.2 湍流模型

本文采用的是重组群

1.3 转动模型

Fluent转动模型主要有动参考系模型（MRF模型）、滑移网格模型和动网格模型。动参考系模型是将不同旋转或移动速度的每个区域进行稳态近似，由于搅拌模型边界上流动区域几乎都是均匀混合，故动参考系适合本文研究的搅拌模型；而滑移网格模型可以处理非定流问题，这是与动参考系模型最大区别，又由于本文研究的颗粒运动是非定常流问题，因此首先采用动参考系模型模拟，待收敛把稳态的结果作为非稳态的初始值，再改用滑移网格模型进行模拟，模拟结果将进一步接近实际运行情况；动网格模型用于模拟由于流域边界运动引起流域形状随时间变化的流动情况，本文不选用此类模型模拟。

图3-1 造粒示意图Fig3-1 The schematic of granulation

2 模型建立

2.1 造粒模拟区域

图3-1为干法造粒机造粒示意图，颗粒在叶片、铰刀和筒体的旋转带动下获得造粒的效果。本文的模拟对象为筒体内气固两相流及造粒过程。筒体内径为135 mm、高为270 mm，铰刀直径8 mm、高为28 mm，叶片厚度为8 mm。

2.2 物理模型与网格划分

由叶片、铰刀和筒体同时都在旋转，故设置两个动区域，一个静区域[9]。本文分析了三种不同主轴偏心率在三种不同筒体倾斜角的物理模型，由于偏心率不同改变了网格的划分，而倾斜角对网格的划分不影响，故只需分别划分三种不同偏心率的模型网格。其中图3-3的网格数为1078162，图3-5的网格数为1075213，图3-7的网格数为1074950。如下图为三种不同主轴偏心率e的物理模型图和网格示意图：

附表1 相关参数设置Tab.1 Related parameter settings

（1）当e1=0时，物理模型图和网格示意图(3-2～3-7)

（2）当e2=0.3时，物理模型图和网格示意图如下

（3）当e3=-0.3时，物理模型图和网格示意图如下

图3-2 e1=0物理模型图Fig.3 -2 he physical model of e1=0

图3-3 e1=0 网格示意图Fig.3 -3 The model grid of e1=0

图3-4 e2=0.3物理模型图Fig.3 -4 The physical model of e2=0.3

图3-5 e2=0.3网格示意图Fig.3 -5 The model grid of e2=0.3

图3-6 e3=-0.3物理模型图Fig.3 -6 The physical model of e3=-0.3

图3-7 e3=-0.3网格示意图Fig.3 -7 The model grid of e3=-0.3

2.3 数值解法与边界条件

利用CFD软件Fluent6.3.26对其进行数值模拟： 求解方法采用耦合隐式求解，时间依赖解采用非稳态模型。在离散化格式中，压力速度耦合插值采用Phase Coupled SIMPLE 算法，动量方程、体积分数、湍动能方程及湍动能耗散率都采用一阶迎风格式。具体边界设置如下（详见附表1）：

（1）区域条件。动域1的转速为1400 rmp(顺时针)，动域2的转速为84 rmp(逆时针)，静域默认设定为静止。

（2）边界条件。叶片壁面、铰刀壁面、筒体壁面、主轴上端轴（静域）、主轴下端轴（动域1）都设置为wall，其中主轴上端轴设定转速为1400 rmp(顺时针)，其它设定为与临近区域一起旋转。

（3）出口边界。出口按照湍流流动充分发展处理，采用自由出流，出口压力为大气压。

（4）固壁边界。壁面为无滑移边界条件，默认壁面粗糙度为0.5，采用标准壁面函数法处理边界湍流。

3 模拟结果分析

图4-1 （α1=0）Fig.4 -1（α1=0）

图4-2 （α2=15°）Fig.4 -2（α2=15）

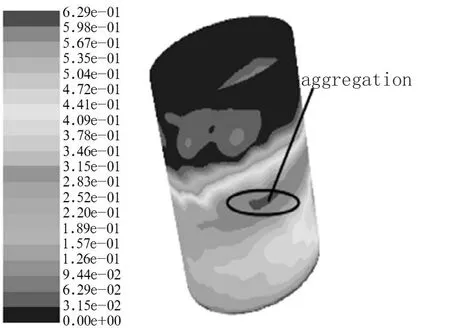
图4-3（α3=30°）Fig.4 -3（α3=30°）

图4-4 （α1=0）Fig.4 -4（α1=0）

图4-5（α2=15°）Fig.4 -5（α2=15°）

图4-6（α3=30°）Fig.4 -6（α3=30°）

图4-7 （α1=0）Fig.4 -7（α1=0）

图4-8（α2=15°）Fig.4 -8 （α2=15°）

图4-9（α3=30°）Fig.4 -9（α3=30°）

3.1 体积分布云图分析

（1）当偏心率e1=0时，干法造粒过程中颗粒的体积分布情况和颗粒团聚现象如下云图所示：

图4-1、4-2颗粒的体积分布情况较好，而图4-3颗粒在筒体的分布体积偏小，同时都存在比较多的颗粒团聚现象。

(2）当偏心率e2=0.3时，干法造粒过程中颗粒的体积分布情况和颗粒团聚现象如下云图所示：

图4-4、4-5、4-6颗粒的分布体积大小依次降低；图4-4、4-5存在少数的颗粒团聚现象，而图4-6颗粒的团聚现象尤为明显。

(3）当偏心率e3=-0.3时，干法造粒过程中颗粒的体积分布情况和颗粒团聚现象如下云图所示：

图4-7、4-8、4-9颗粒的体积分布情况很好，但是图4-9存在颗粒的溢出现象；图4-7存在一定的颗粒团聚现象，而图4-8几乎不存在颗粒团聚现象。

3.2 模拟结果分析

3.2.1 主轴偏心率对搅拌效果的影响

当筒体倾斜角恒定不变时，通过改变主轴偏心率模拟干法造粒机在造粒的过程中颗粒的体积分布情况与颗粒团聚现象，分析主轴偏心率对颗粒分散性的影响，具体如下：

(1）当倾斜角 时，由图4-1、4-4、4-7可知，体积分布情况大致相同。但图4-1在筒体上端存在比较多的颗粒团聚现象，图4-4、图4-7在筒体下端也存在少量的颗粒团聚现象。模拟结果分析表明，当倾斜角 时，主轴偏心率对颗粒的体积分布情况影响不大，但是对颗粒的团聚现象影响还是较大，适当的偏心率可以减少颗粒的团聚现象发生。

(2）当倾斜角 时，由图4-2、4-5、4-8可知，体积分布情况大致也是相同。但图4-2在筒体上端存在比较多的颗粒团聚现象，图4-5在筒体下端存在少量的颗粒团聚现象，而图4-8在筒体内几乎不存在颗粒团聚现象。模拟结果分析表明，当倾斜角 时，主轴偏心率对颗粒的体积分布情况影响不大，但是对颗粒的团聚现象影响很大，恰当的偏心率几乎可以消除颗粒的团聚现象发生。

（3）当倾斜角 时，由图4-3、4-6、4-9可知，图4-3、4-6颗粒体积分布情况较差，图4-9颗粒体积分布情况较佳，但是存在颗粒溢出现象。图4-3、4-6存在较多的颗粒团聚现象。模拟结果分析表明，当倾斜角 时，主轴偏心率对颗粒的体积分布情况影响很大，随着偏心率的增大，颗粒的分布体积越小。相反，随着偏心率的增大，颗粒的团聚现象越明显。

3.2.2 筒体倾斜角对搅拌效果的影响

当主轴偏心率恒定不变时，通过改变筒体倾斜角模拟干法造粒机在造粒的过程中颗粒的体积分布情况与颗粒团聚现象，分析筒体倾斜角对颗粒分散性的影响，具体如下：

(1）当偏心率e1=0时，由图4-1、4-2、4-3可知，颗粒分布体积大小依次减小。同样，颗粒的团聚现象依次更明显。模拟结果分析表明，当偏心率e1=0时，筒体倾斜角越大，颗粒的分布体积反而越小，而颗粒的团聚现象越明显。

(2）当偏心率e2=0.3时，由图4-4、4-5、4-6可知，颗粒分布体积大小依次锐减更大。同样，颗粒的团聚现象也依次越发明显。模拟结果分析表明，当偏心率e2=0.3时，筒体倾斜角越大，颗粒的分布体积大小锐减，而颗粒的团聚现象越发明显。

(3）当偏心率e3=-0.3时，由图4-7、4-8、4-9可知，图4-7、4-8颗粒的体积分布情况较佳，而图4-9颗粒已从筒体口溢出。模拟结果分析表明，当偏心率e3=-0.3时，筒体倾斜角越大，颗粒的体积分布情况越好，但是倾斜角大到一定程度，颗粒将从筒体口溢出。而颗粒的团聚现象随着倾斜角增大越来越不明显。

4 结 论

(1)由模拟结果分析可得，在主轴偏心率为-0.3、筒体倾斜角为15°时，颗粒的体积分布情况最佳，且几乎没有颗粒的团聚现象发生。

(2)在干法造粒过程中，筒体倾斜角对造粒过程颗粒的体积分布情况与颗粒的团聚现象有很大的影响，适当设定一定角度的倾斜角有助于颗粒的充分分散。

(3)在干法造粒过程中，主轴偏心率对造粒过程颗粒的体积分布情况与颗粒的团聚现象影响很大，特别是颗粒的团聚现象。

(4)通过数值模拟优化设计主轴偏心率和筒体倾斜角，在一定程度上得出了最佳组合。能够很好的解决干法造粒机颗粒的充分分散性问题，使得干法造粒的粉料流动性、强度、堆积密度等物理性能更加符合产业要求。同时对陶瓷行业节能降耗、生态环境与产业协调发展等方面具有十分重要的意义。

[1] 李绍勇，周荣光，梁飞峰. 超细化干法造粒制备陶瓷粉料技术[J]. 佛山陶瓷， 2010(08)： 20-22.

LI Shaoyong， et al.， Fushan Ceramics， 2010(08)： 20-22.

[2] 孙海发.关于干法造粒工艺在陶瓷行业应用的答疑[J].佛山陶瓷. 2010(09).

SUN Haifa. Fushan Ceramics， 2010(09).

[3] H LLERI N， MANFREDINI U， SIKALIDIS C. Dry tech mutiline： an evolution in raw materials preparation for ceramic tiles[J]. International Ceramic Journal， 2009，10(2)： 93-96.

[4] JUNG C H， PARK J Y， KIM W J， et al. Characterizations ofprepared by a solution combustion synthesis and fabrication of spherical particles by dry-rolling granulation process[J]. Fusion Engineering and Design， 2006， 81(8-14)： 1039-1044.

[5] GIANFRANCO CARNEVALI，PAOLO ZANNINI. 干法制备压型粉料的革新工艺[J].国外建材科技，2006(03)：30-32.

[6] HUTT E. Dry granulation of ceramic materials[J]. Steklo I Keramika， 1965， 22(2)： 43

[7] 江帆，黄鹏.Fluent 高级应用与实例分析[M].北京：清华大学出版社， 2008(07).

[8] 李进良， 李承曦， 胡仁喜. 精通FLUENT6.3流场分析[M].北京： 化学工业出版社， 2009(09).

[9] 王蕊. 种分搅拌槽内多相流体流动的数值模拟[D]. 东北大学硕士学位论文.

[10] 张柏清， 赖泽标. 基于正交试验法对干法造粒颗粒大小影响因素的分析[J]. 陶瓷学报， 2013(01).

ZHANG Baiqing， et al.， Journal of Ceramics，2013(01).

Numerical Simulation and Optimized Design of Dry Granulator for Ceramic Materials

WU Nanxing, LIAO Dahai, XIAO Zhifeng
(School of Mechanical and Electronic Engineering, Jingdezhen Ceramic Institute, Jingdezhen 333403, Jiangxi, China)

:The substitution of dry granulation of the ceramic materials for high energy consumption, high pollution wet milling-spray drying granulation is an inevitable trend in ceramic industry. In order to realize full de-agglomeration in the process of dry granulation, 3D mathematic models based on the Eulerian two-fuid model were developed using the commercial CFD software pack. The volume distribution and agglomeration of the granules are simulated by the models of the major axis eccentricity and the cylinder inclination angle generated via a fnite volume route. Results show that when the eccentricity is -0.3 and the incline angle is 15°, the granules are best dispersed. The optimized design through numerical simulation has virtually realized the full de-agglomeration of the dry granulation. It will provide a theoretical basis for the development of a dry granulator for ceramic materials.

Eulerian two-fuid model; numerical simulation; full de-agglomeration; optimized design

WU Nanxing(1968-),male,Ph.D.,Professor.

TQ174.5

A

1000-2278(2014)01-0082-06

2013-10-25。

2013-10-30。

国家自然科学基金资助（编号：51365018）

吴南星(1968-)，男，博士，教授。

Received date:2013-10-25. Revised date:2013-10-30.

E-mail:wnx1968@163.com