基于非参数方法的保险产品障碍期权定价研究
游桂云,冯 晶
(1.对外经济贸易大学 保险经济学院,北京100029;2.中国海洋大学 经济学院,山东 青岛 266100)
1 保险产品障碍期权定价原理
传统财产-责任保险定价多采用精算方法,需要通过一定的模型来预估损失发生率和平均损失额。由于环境责任保险事故发生的概率少,基础数据少,难以得到大量的索赔数据,一定程度影响了环境责任保险定价。精算得到的只是纯费率,为了控制风险则需要进行较高的风险附加和费用附加,这样种仅考虑供给方利益的费率对投保人是不利的。期望均衡原理,是建立在供求基础上的现代保险精算,兼顾供给方和需求方的利益,可以有效解决上述问题。由于环境责任损失发生概率小,一旦发生损失额较大的特点,可以假定被保险人在保险期内最多索赔一次,这样就可以应用期权定价模型计算保险费率。
投保人和保险公司签订的保险合同,实质上就是一份期权合约。为体现保险的补偿性原则、增强投保人的安全防范意识、控制损失概率增大以及杜绝故意行为,保险合约中往往设有免赔额和保险金额即保险人承担赔偿或者给付保险金责任的最高限额。对于这一类保险,保险的免赔额相当于起付线,起付线以上的损失由保险公司对保险人给予赔付,承担赔付责任。同时规定有最高给付限额即保险金额,当损失超过最高限额时,原期权失效但给予相应补偿,这个补偿金额通常设定为保险金额。本文引入的障碍期权是不同于标准期权的新型期权,是一种附加条件的期权,对其附加条件的目的在于把投资者的收益或损失控制在一定范围之内。具体来讲就是在普通期权的基础上嵌入一个障碍价格,当标的资产价格触及障碍价格时,期权合约失效或生效,如果标的资产价格在期满前一直没有触及障碍价格,则等价于普通期权[7]。其中障碍价格高于执行价格,即标的资产价格上升达到障碍价格后该期权失效(或生效)的称为向上敲出(或敲入);反之则为向下敲出(或敲入)。
将保险合约视为一个向上敲出的看涨期权,保险公司收取的保费相当于该期权的价格,此时标的资产则转化为被保险人的损失金额。假定Pt为t时刻的保费,C(St,t)为看该时刻的看涨期权价格,St为损失金额(标的资产价格),X为保险合约中的免赔额(期权的执行价价格),到期日为T(T>t)。根据保险精算方法确定的该期权的价值是未来标的资产价格大于执行价格产生潜在损失和请求权的数学期望值,故该向上敲定的看涨期权到期时期权价值为:

令保险赔付额ST-X=x,则上述看涨期权可转化为:标的资产在t时刻的价格为x(赔付额),期权的执行价为0,到期日为T(T>t),障碍价格为H的看涨期权。规定在保险有效期内,当保险人赔付金额x低于执行价格0时,不执行期权;当保险人赔付金额超过0时投保人则执行期权,保险人对超过部分x进行赔付,同时规定最高赔付限额H,一旦损失额触及障碍价格(赔付上限),但按保险金额H给予相应的现金补偿,即当ST≥H时只赔付H-X。
根据保险精算方法确定的该期权的价值是未来标的资产价格大于执行价格产生潜在损失和请求权的数学期望值,故该向上敲定的看涨期权到期时期权价值为:

2 基于非参数核密度估计的障碍期权定价模型推导
2.1 基于非参数方法的损失分布确定
基于非参数方法的障碍期权定价模型推导,应用非参数核密度估计法对环境责任保险损失分布进行估计是关键,本文将保险赔付额x视为标的资产价格,并选择非参数估计中的Parzen核密度估计方法进行损失分布拟合,具体步骤如下:
(1)选取核函数:
设x为给定的随机变量,hn(hn→0)是一个常数(称为为窗宽),则称:

(2)最优窗宽的选取:
式(6)中hn为信息扩散系数也称窗宽,即组间宽度参数(Band-width),决定了密度函数的平滑程度,宽度参数的确定是非参数核密度估计的重要步骤。
选择组间宽度参数的方法有总量确定法、“Silverman经验法”和插入法。本文采用Silverman的经验法则(SROT),考虑最小化积分均方误差(MISE),宽度参数一个较好的选择为:

2.2 向上敲出障碍期权的价格
根据前文的分析得到财产-责任保险对应的障碍期权价格为:


其中φ(u)为标准正态密度函数,Φ(u)为标准正态分布积累函数。
根据上式可以发现,通过基于非参数方法的期权定价模型对保险产品费率进行厘定时,其价格取决于免赔额X,保险金额H,承保时间(T-t)、无风险利率r,宽度参数hn的选择以及损失的分布情况。其中免赔额的设定有利于投保人提高风险防范意识,降低风险事发生的可能性,因此,设定免赔额可以降低保险费率。 保险金额在期权合约中是固定不变的。保险金额即最高赔付限额越高,则被保险人获利的可能性越高,保险的价格越高。承保时间反映了期权合约的时间价值,一般而言,距到期日的时间越长,保险的时间价值越大。无风险利率一般指国债的发行利率或银行1年期定期存款利率,它是购买期权的机会成本。因此无风险利率的高低反应了保险合约机会成本的大小,高利率要求期权的高收益率,相应地保险价格也越低。
3 实证测算
由于企业导致的环境污染事故的发生而导致第三者蒙受损失,企业需要依法承担一定的赔偿责任,以这种责任为标的的责任保险即为环境污染责任保险。在环境责任保险制度中,投保企业向保险公司提前缴纳一定数额的保险费,保险公司则根据保险合同的内容承担赔偿责任,如果被保险人发生环境污染事故,对第三者的身体健康和财产造成了损失,则对于免赔额以上保险金额以下的损失和治理费用保险公司直接向第三者提供赔偿金。
根据前文的理论分析,环境责任保险这一含有免赔额及最高保险限额的责任保险可视为一个向上敲出的看涨期权。环境责任保险的保费即为障碍期权的价格,其中免赔额相当于期权执行价格X,规定在保险有效期内,当投保人损失金额ST低于执行价格X时,投保人不执行期权;当投保人损失金额额超过免赔额时投保人则执行期权,保险人对超过部分ST-X赔付,同时规定保险金额(障碍价格)H,一旦损失金额触及障碍价格(赔付上限),但按固定金额H-X给予相应的现金补偿,即当ST≥H时只赔付H-X。
在我国的实践中,以那些高污染行业作为环境责任保险试点的重点行业,对部分行业甚至推行法定强制环境责任保险。因此本文选取化学原料及化学制品制造业这一高污染行业作为环境责任保险期权定价的研究对象,假设在该行业推行强制性环境责任保险,即该行业全部国有及规模以上非国有工业企业均作为投保人。对历年来我国的环境责任事故进行损失计算,并加以处理,得到实证数据,在此基础上进行保险费率的厘定研究。
3.1 数据来源和处理
根据李生才、王亚军、黄平等人统计在2004~2012年《安全与环境学报》上的环境污染事故,并结合原始事件相关报道,分别对相关环境责任事故进行损失计算,得到2004-2012年期间相关事故的损失数据。
对计算得到的损失数据加以整理和筛选,其中损失金额小于5万元的不予列出,损失金额在5万元至200万元之间的,将之减去5万元列出,损失金额大于200万元的按195万元列出,得到2004~2012年化学原料及化学制品制造业的环境污染事故的赔偿金额及次数(见表1)。

表1 保险公司对每次事故的赔付额 (单位:万元)
根据实证数据的需要对这些损失数据进行相应的处理。对环境责任保险的保险标的进行分析,对于一份环境责任保险而言,其保险标的是某一投保企业在一定时间区间内造成的环境事故损失赔偿金额。所采用的实证数据必须与之相对应,然而目前已有的数据是每次事故的损失数据,因此,采用如下方法对实证数据进行处理:首先,确定某一特定时间区间为承保期,由于目前已有数据是2004~2012年的年度数据,以年度数据进行计算则实证数据太少,不利于实证研究,所以研究采取2个月作为承保期;其次,对2004年1月至2012年4月期间内每两个月的赔偿数据进行加总,得到每两个月一次的全国范围内环境责任事故赔偿总额,共50个数据;再次,由于在期权定价中确定的是一份期权的价格,因此相应的实证数据也应该是一个企业的受偿金额,所以将上一步骤得到的数据除以该年份化学原料与化学制品制造业企业的数量,得到一家企业在以2个月为一期间的50个期间内所造成的保险公司的赔偿金额;最后,由于2004~2012《安全与环境学报》中化学原料与化学制品制造业的环境污染事故的统计次数偏少,相当于同期《中国环境统计公报》统计数据的1/4。因此本文将其调至《国内环境事件数据》统计次数的4倍,即以《中国环境统计公报》统计数量为准,得出研究所需的实证数据,如表2所示。
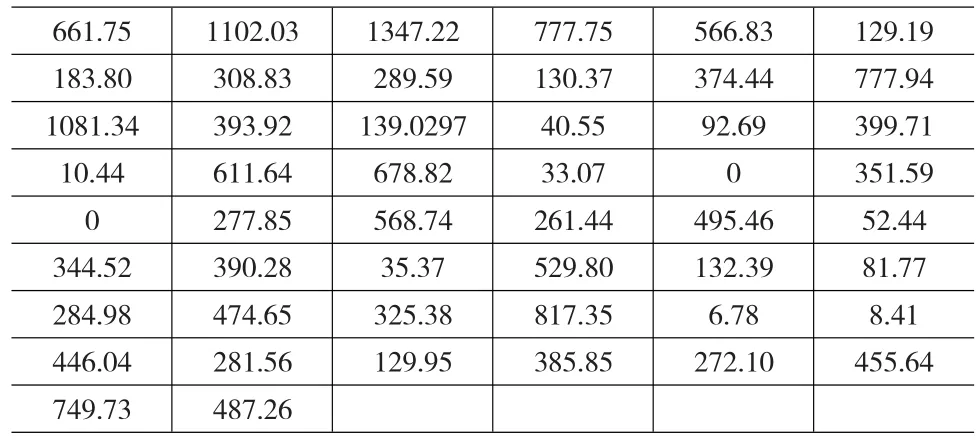
表2 以两月为一个统计区间的事故赔偿金额 单位:元
3.2 相关数值设定
(1)免赔额与保险金额
在环境责任保险中保险金额和免赔额的设定始终是个难点,笔者(2010)在《环境责任保险模式选择与定价研究》一书中根据国外环境责任保险金额确定的经验和我国保险市场的发展情况指出:根据对化学原料及化学制品制造业环境污染事故的统计,约90%事故的损失在5万元以上,对于生产规模在500万以上的企业,在考虑企业的承保能力和促进其投保积极性的前提下,确定其保险金额为200万元,基本免赔额为5万元。本文仍将免赔额设定为5万元,承保金额设定为200万元,采用绝对免赔额的定义,即如果一次事故损失不足5万元,则保险公司不进行赔付;如果损失为a万元(5<a<200),则保险公司赔付(a-5)万元;如果损失金额大于200万元,则保险公司赔付195万元
(2)无风险利率的确定
选择以最近的SHIBOR利率为无风险利率(设为r0=4.4002%)由于B-S模型中无风险利率必须是连续复利(设为r0=4.4002%)形式,因此需要将一个简单的无风险利率转化成连续复利的形式,换算关系如下:

3.3 环境责任保险费率厘定及结果分析
根据本研究在第3部分中已经推导出的费率厘定公式,并将上述计算得到的参数代入得:

由于经过上式计算的结果是两个月的保费金额,因此要得到一年期环境责任保险的保费,应当将每个两月期的保费均贴现至当年初,计算如下:

按照1.12‰的保险费率和统计得到的损失数据计算得到2004-2011年期间,全国范围内环境责任保险的预计保费收入和预计赔付金额,并据此计算得到预计承保利润,表3所示。

表3 2004-2011年全国环境责任保险利润估算表 (单位:万元)
可以发现,除2004年出现约3500万元的巨额亏损外,其他年份保险公司,均有一定的利润,总体而言,2004~2011年,全国的环境责任保险预计利润合计3719.53万元,既保证了保险公司的承保利润空间,又没有对投保人的利益产生严重损害,基本保持平衡状态。因此,1.12‰的保险费率是较为科学和合理的。
4 研究结论
本文通过分析含免赔额及最高赔付限额的一类财产责任保险的期权特性,将更加契合保险特性的一种特殊期权——障碍期权引入保险产品定价。将保险合约视为一种向上敲出的看涨期权,并利用精算与期权定价相结合的方法,通过非参数核密度估计方法估计损失分布情况,推导出基于非参数方法的障碍期权定价模型,进而调整为保险期权定价模型。这与基于对数收益率服从正态分布的Black-Scholes定价不同。由于资产价格的分布往往不是严格服从对数正态分布的,这就使得Black-Scholes定价在保险定价的运用中存在一定的局限性。本文采用非参数方法对资产价格分布进行非参数估计,其分布函数是从历史损失数据中得到的,这是比较贴近市场的定价方法。
此外,以目前国内正在试点的环境责任保险为例,选择其中的重点行业——化学原料及化学制品制造业作为实证对象。对2004~2012期间环境污染事故数据进行处理,利用推导得到的基于非参数方法的障碍期权定价模型进行环境责任保险定价实证研究,得出相应的费率水平。经过一定的合理性检验得出:总体而言按照本文测算出的费率水平,既保证了保险公司的承保利润空间,又没有对投保人的利益产生严重损害,基本保持平衡状态。
[1]Cummins J David.Risk-based Premiums for Insurance Guaranty Funds[J].The Journal of Finance,1988,43(4).
[2]Alexandre Ziegler.A Game Theory Analysis of Options[M].Springer Verlag,1999.
[3]Grosen Anders,Jorgensen P Lochte.Fair Valuation of Life Insurance Liabilities:The Impacts of Interest Rate Guarantees Surrender Options and Bonus Policies[J].Insurance:Mathematics and Economics,2000,(26).
[4]Calum Turvey,Jinhua Zhao.Parametric and Nonparametric Crop Yield Distributions and Their Effects on All-Risk Crop Insurance Premiums[Z].Working paper,Department of Agricultural Economics and Business University of Guelph,1999.
[5]郑红.基于期权定价视角的医疗保险精算原理与方法[J].系统工程,2011,(2).
[6]梁来存.我国粮食保险纯费率厘定方法的比较与选择[J].数量经济技术经济研究,2011,(2).
[7]游桂云,赵智慧,戴雷奇.环境责任保险精算定价实证研究[J].统计与决策,2012,(5).
——方靶心图

