基于非对称模糊PI控制的光伏发电MPPT研究

杨海柱，刘 洁，曾志伟，姚君旺

（1.河南理工大学电气工程与自动化学院，河南焦作 454000；2.河南理工大学计算机科学与技术学院，河南焦作 454000；3.六盘水师范学院 物理与电子科学系,贵州六盘水 553004）

光伏发电具有无污染、无噪音等优点，越来越受到关注。制约光伏发电系统发展的主要因素是能量转换效率问题，所以提高光伏阵列的光电转换效率并使其输出功率最大化，即在理论和实践上提出了光伏阵列的最大功率点跟踪问题。由于传统方法的局限性，本论文采用智能控制方法的智能性、自适应性来对非线性光伏发电系统进行控制，无疑是一个很好的选择[1]。

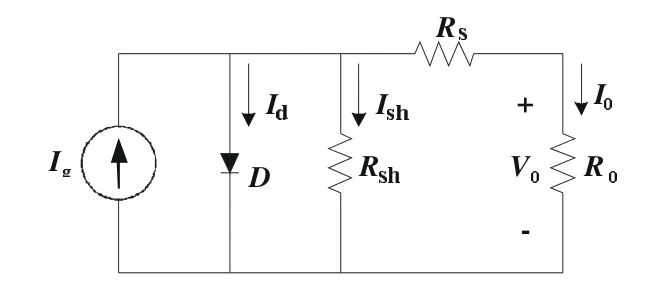
图1 太阳电池等效电路

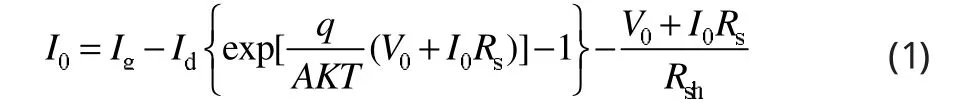
1 太阳电池阵列特性

太阳电池是一种光电转换的半导体装置，其产生的电压和电流分别受温度和光照强度的影响。当受光照射的太阳电池接上负载时，光生电流流经负载，并在负载两端建立起端电压。这时太阳电池的工作情况可用图1所示的等效电路来描述。

当流进负载R0的电流为I0，负载的端电压为V0时，由太阳电池的等效电路图可以得到如下的解析式：

式中：Ig为光生电流；Id为二极管饱和电流；q为电荷电量 (1×10－19C)；A为二极管因子；K为波尔兹曼常数 (1.38×10－23焦耳/度)；T为开氏温度(K)；V0为电池的输出电压；I0为电池的输出电流；Rs为等效串联电阻；Rsh为等效并联电阻。

根据光伏电池等效电路图建立其仿真模型，调节电阻负载的大小进行采样，当光照变化时光伏阵列的I-V特性曲线和P-V特性曲线如图2所示[2]。从图中可以看出在温度不变的条件下，光伏电池的开路电压随光照的降低而下降，短路电流和光照成正比，最大输出功率随光照的升高而剧增。

2 基于非对称模糊PI控制原理及实现

常用的最大功率跟踪控制算法有恒电压跟踪算法(CVT)、干扰观察法(P&O)、增量电导法(IC)等。对于那些时变的、非线性的复杂系统，当无法获得精确的数学模型时，利用具有智能特性的模糊控制器能给出有效的控制[3-5]。

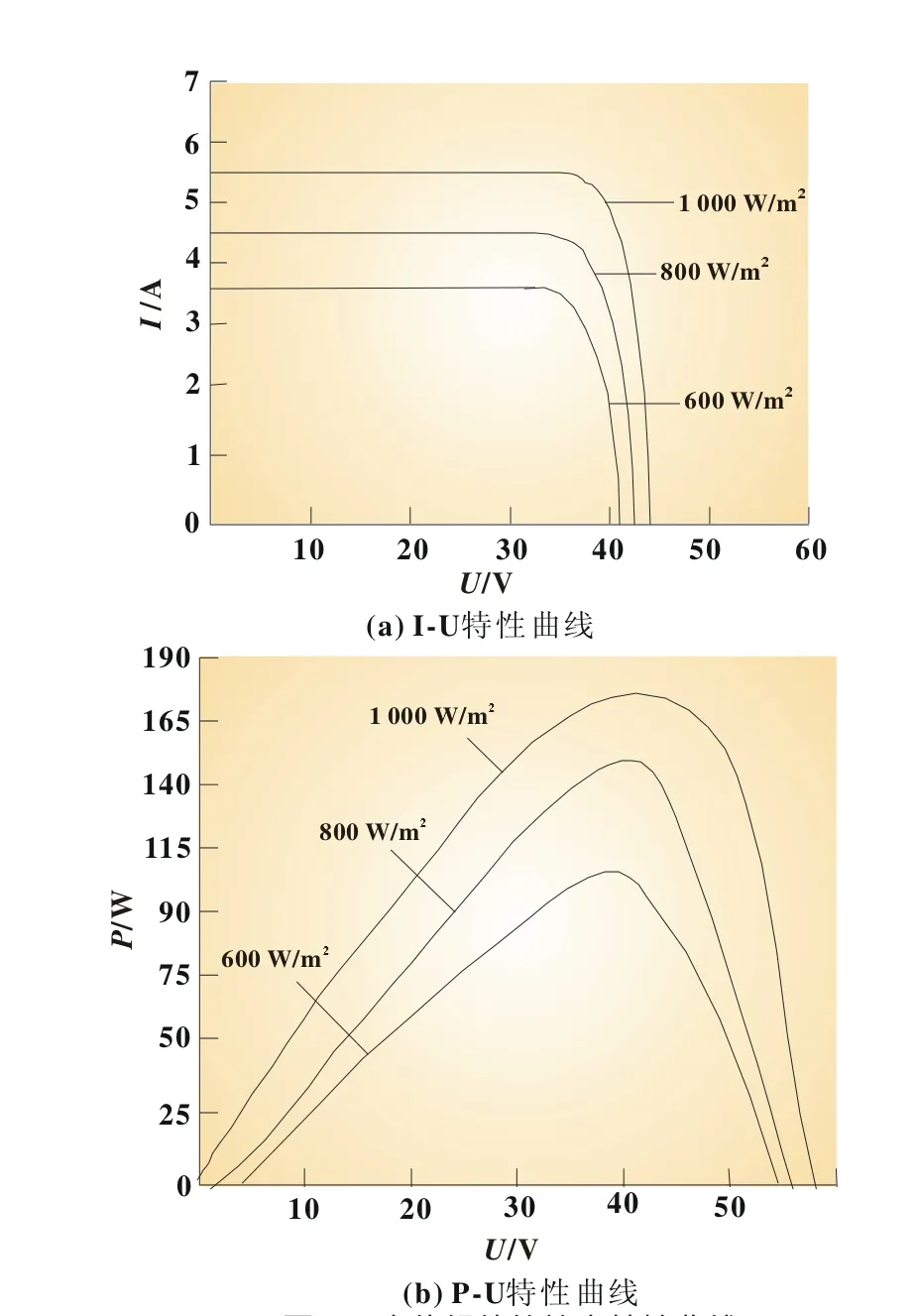
图2 光伏组件的输出特性曲线

光伏电池输出功率见公式(2)，公式(3)是输出功率对输出电压的导数d P/d V，表明该导数是输出电压的单调函数。当输出电压为零时该值最大，大小等于电池的短路电流；随着输出电压的增加，d P/d V缓慢下降，在输出功率最大点附近该值下降速度加快，在MPP点该值等于零；随着输出电压V进一步增加，d P/d V变为负值，绝对值快速上升远大于曲线在最大功率点左侧的值，特性曲线见图3。公式(2)和图3表明最大功率点两侧相同电压变化△V造成的功率变化有很大差异，因此在最大功率点两侧应该采用不同的占空比△d，实现光伏电池最大功率跟踪。

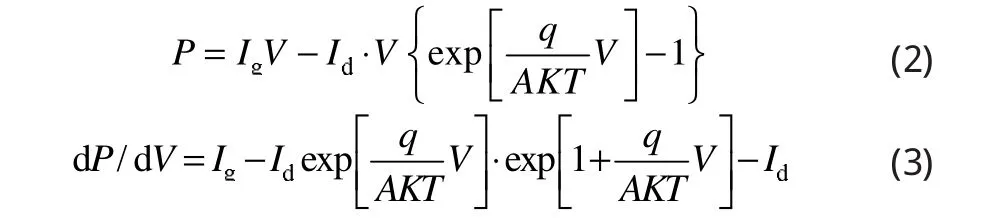
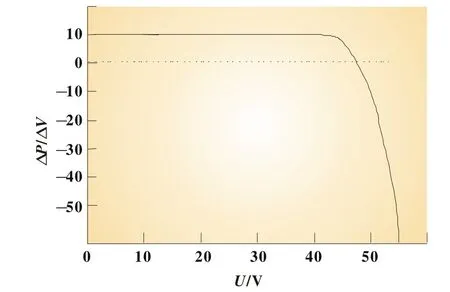
图3 光伏电池d P/d V-V特性曲线

因此根据光伏电池的特性将非对称模糊-PI控制应用到光伏电池的最大功率点跟踪，它在最大功率点两侧采用不同的控制策略和隶属度函数，可以有效消除功率振荡现象。本文提出的非对称模糊PI控制系统如图4所示[6]。

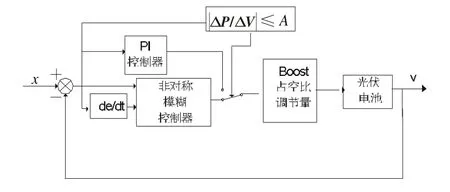
图4 非对称模糊PI控制原理图

2.1 非对称模糊控制器的设计

2.1.1 模糊控制器的输入量和输出量

模糊控制器两个输入分别是误差e和误差变化ec，见公式(4)。输出为MPPT电路中开关器件占空比的改变量△d。

2.1.2 量化因子和比例因子

为便于控制，分别对误差e和误差变化ec的实际值进行量化，用比例因子把模糊控制器的输出转化为MPPT电路开关占空比的变化量△d，然后映射到模糊集合论域Ep和Ed。

e，ec的论域均为{－0.5,0.5}，△d的论域为{－0.01，0.01}

2.1.3 隶属度函数

根据光伏电池的特点，本文误差选用非对称的隶属度函数，为了便于实现和保证系统可靠运行，输出采用梯形隶属度函数，如图5所示。

图5 隶属度函数

2.1.4 模糊决策表和解模糊方法

选取控制量的原则：当误差大或较大时，选择控制量以尽快消除误差为主；当误差较小时，选择控制量要注意防止超调，以系统稳定性为主要出发点。确定了输入和输出控制量之后，下一步是设计模糊控制器的控制规则。在本方案中，模糊推理采用Mamdani方式，解模糊方法为面积重心法。最后得到模糊规则表，如表1所示。

2.2 非对称模糊-PI控制仿真图

通过Matlab的Fuzzy Logic工具箱可以建立模糊子系统。采用非对称模糊控制算法通过占空比来调整最大输出电压的同时，需要考虑占空比的步长，步长过大，精度达不到要求，稳态误差变大；步长过小，跟踪时间过长，易在MPP点附近反复振荡，为了最终达到自动寻优的效果。设计了非对称模糊-PI系统，其仿真图如图6所示。根据论域和变量实际取值范围，e和ec的比例因子都为0.1，△d的比例因子为10，根据经验，|△P/△V|≤A中，A取 0.06，仿真时间设置为 0.01 s，延时时间为0.000 02 s。通过多次仿真实验得出，当比例系数kp=0.01，ki=1时，PI控制器能够达到较好的控制效果[7]。

3 仿真结果分析

设定初始条件：以NT-R5E3E 175W太阳电池板为仿真目标；G=1 000W/m2，T=25℃。采用占空比扰动法和非对称模糊控制法的功率输出曲线如图7和图8所示。从图7中可以看出，系统从初始功率0W上升到功率175W，并在0.01 s左右达到稳定状态，并伴随有较大功率振荡；在t=0.1 s时，当光强突变到G=800W/m2，系统在0.11 s左右达到最大功率点并稳定于140W左右。从图8可以看出，加入模糊控制之后，响应速度明显加快了，最大功率点处功率振荡明显减少。非对称模糊-PI控制的输出功率跟踪曲线如图9所示。通过仿真对比发现，都能跟踪系统最大功率点，占空比扰动法响应速度慢，适合光照强度变化缓慢的场合，并且在稳态情况下，会导致光伏电池的实际工作点在MPP点的附近振荡。加入非对称模糊-PI控制之后，能够有效地提高动态系统特性和精度，快速跟踪最大功率点，消除最大功率点处功率振荡，稳定性好。

图7 功率输出

图8 功率输出

图9 功率输出

4 结论

本文针对光伏电池的非线性特性曲线，以及传统最大功率点跟踪方法的不足，应用智能、自适应性控制方法，将非对称模糊-PI控制应用于光伏电池MPPT中。通过仿真验证：该方法在外界环境变化剧烈的情况下，快速跟踪光伏电池的最大功率点同时能基本消除最大功率点的功率振荡现象，具有较高的控制精度和稳定性。

[1]沈辉,曾祖勤.太阳能光伏发电技术[M].北京:化学工业出版社，2005.

[2]茆美芹,余世杰,苏建徽.带有MPPT功能的光伏阵列Matlab通用仿真模型[J].系统仿真学报，2005,17(5):1248-1251.

[3]苏义鑫，向炉阳，张丹红.基于改进扰动法的光伏电池MPPT仿真研究[J].武汉理工大学学报，2012(4)：135-139.

[4]XIAOWD,DUNFORD WG.A modified adaptive hill climbing MPPT method for photovoltaic systems[C]//35th annual IEEE Power Electronic Specialists Conference.Germany,IEEE：2004,1957-1963.

[5]TAFTICHT T,AGBOSSOU K.Developmentof aMPPTmethod for photovoltaic systems[C]//Electrical and Computer Engineering,2004 Canadian Conference.Canada,Electrical and Computer Engineering：2004,5(2):1123-1126.

[6]SIMOESMG,FRANCESCHETTIN,FRIEDHOFERM.Fuzzy logic based photovoltaic peak power tracking control[C]//Proc IEEE Conf International Symposium on Industrial Electronics.Pretoria：IEEE，1998,300-305.

[7]张超,何湘宁.非对称模糊PID控制在光伏MPPT中的应用[J].电工技术学报，2005,20(10):72-75.