“数控机床可靠性技术”专题（十四） 可靠性评估技术

张根保 康丽娜

（重庆大学机械工程学院，重庆 400044）

1 可靠性评估概述

1.1 可靠性评估的概念

可靠性评估是根据产品的寿命分布类型以及与产品的可靠性有关的所有信息（包括产品的使用经验信息和样本的可靠性试验信息），利用概率统计方法对产品总体的可靠性指标进行统计推断，包括点估计、区间估计和假设检验等[1]。可靠性评估技术是可靠性增长环节中的一个重要组成部分，正确地评估产品现有可靠性水平，才能不断地发现产品存在的问题，为改进和提高产品性能和可靠性提供依据，生产满足用户需求的高质量产品。

1.2 可靠性评估的目的和意义

数控机床的可靠性是实现其功能，为机床制造企业和用户创造经济效益的重要保障，而可靠性评估是数控机床可靠性研究的重要组成部分，为可靠性工程的各项活动提供理论支撑和数据基础。对数控机床进行可靠性评估的目的和意义在于：

(1)科学而先进的可靠性评估方法，为充分利用各种试验和故障信息奠定了理论基础。对减少试验经费，缩短研制周期，合理安排试验项目，协调系统中各单元的试验量等有重要的作用。

(2)通过评估，检验产品是否达到了可靠性要求，并验证设计的合理性，如可靠性分配的合理性，选用元器件、原材料及加工工艺的合理性等等。

(3)通过评估，可以发现产品的薄弱环节，为改进设计和制造工艺指明方向，从而加速产品研制的可靠性增长过程。

(4)通过评估，了解有关元器件、原材料、整机乃至系统的可靠性水平，为制定新产品的可靠性计划提供依据。

(5)通过评估可以比较不同企业的产品可靠性水平，为用户选择产品提供依据。

(6)可靠性评估工作需要进行大量的数据收集、对数据进行分析及反馈，从而可以加强数据库及信息网络的建设。

2 数控机床可靠性评估技术

2.1 产品寿命周期可靠性评估

可靠性评估是数控机床全寿命周期各阶段都需要进行的一项可靠性工作，根据其寿命周期划分为3个阶段：

(1)研制阶段：收集处理可靠性试验数据和相似产品的故障历史数据，通过评估了解机床研发过程中的可靠性水平是否达到规定的要求。

(2)生产阶段：利用机床的验收试验数据进行可靠性评估，检验其生产工艺和质量控制能否保证产品达到设计确定的可靠性水平。

(3)使用阶段：需要收集机床的故障数据，进行数据分析和可靠性评估，找出其故障时间的概率分布，以进一步分析产品故障、预测故障发展、研究其失效机理，为产品改进、产品维修策略等提供决策依据。

2.2 可靠性评估的一般流程

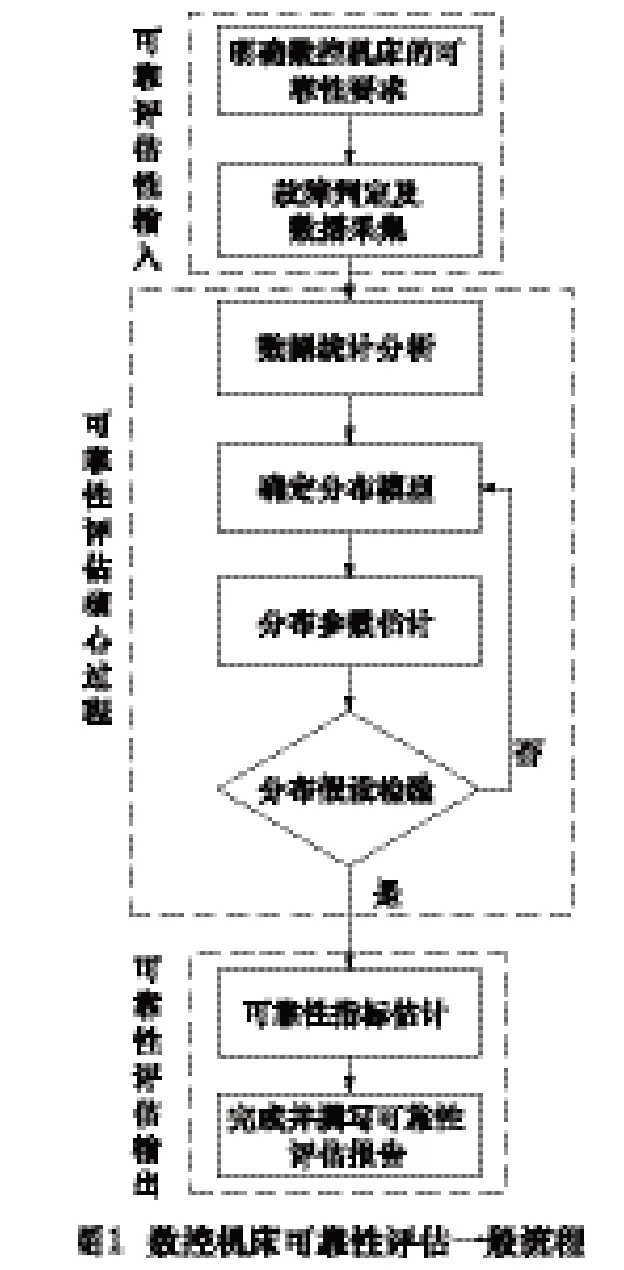
数控机床可靠性评估的基本流程如图1所示。

(1)明确数控机床的可靠性要求，包括设计确定的可靠性指标。

(2)明确数控机床的故障判定原则和故障计数原则，并对故障数据进行采集。

(3)对采集的数据进行统计分析，以确定可靠性评估的分布模型，如威布尔分布、幂律过程等，需特别注意数据贫乏的情况。

(4)利用最大似然估计法、最小二乘法等对可靠性评估分布模型的参数进行估计，可借助Weibull++、Mathematica、Matlab等数学软件。

(5)根据参数估计值求得可靠性评估模型，并对其进行假设检验，检验通过则可进行可靠性指标的求解及分析，检验不通过则需要重新确定分布模型。

(6)数控机床的可靠性指标包括可靠度、可靠寿命、MTBF等，通过对指标的求解结果，分析待评估数控机床的可靠性水平。

3 可靠性评估的技术关键点

3.1 可靠性评估输入

可靠性评估输入主要指通过可靠性数据来源，采取一定的收集程序及方法获得数据，对数据进行进一步处理，包括数据的筛选、清洗与提取，最终获得能够用来进行可靠性评估的数据（包括机床的使用时间、故障模式、故障间隔时间、故障发生时间、维修时间等）。可靠性评估数据可以来自制造现场、实验过程和用户使用过程。输入数据的质量将直接影响评估结果的准确性，而输入数据的数量将直接影响评估方法的选择，如图2所示。

(1)数据充足：对于有效数据的量足够的情况，可以直接对数据进行统计分析（如直方图），并运用相应的方法与模型（详细见3.2.1与3.2.2）进行可靠性评估。

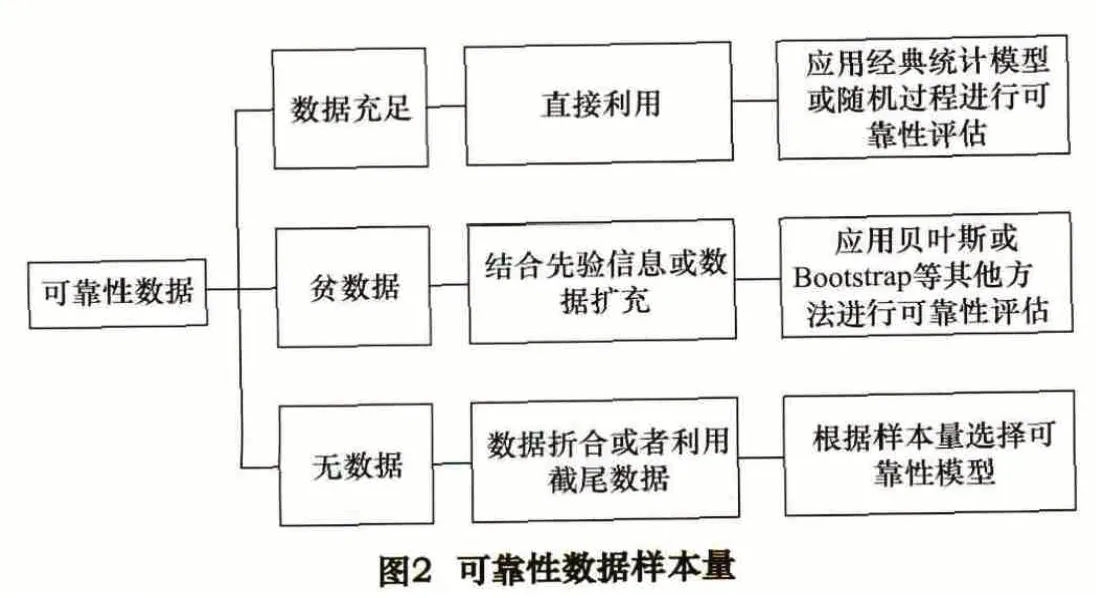
(2)贫数据：数控机床属于多品种、小批量产品，往往还具有定制的性质，且数控机床的寿命周期较长，很难获得大量的、具有可比性的故障数据。因此，数控机床的可靠性评估往往具有小样本数据的特征。需要采取数据扩充的方法获得足以进行评估的数据量。

(3)无数据：这种情况往往出现在试验过程中。对于高可靠性、高质量数控机床，在定时截尾试验下，有可能出现无故障的情况。多数无故障数据的可靠性评估是在分布类型已知的定时截尾试验条件下进行的。在这种情况下，一般不建议进行可靠性评估，因为评估结果的可靠度并不高，但也有学者通过可靠性试验利用故障征兆进行可靠性评估。

3.2 可靠性评估方法介绍

可靠性评估技术的核心环节是可靠性模型的建立，许多研究者在这一领域进行了大量的理论与实践应用研究。通常来说，三类方法常被用于研究机床可靠性。

3.2.1 寿命分布分析法

(1)寿命分布分析法，即通过拟合机床故障数据所属的最优分布函数，进而获得相关可靠性指标的方法。该方法来源于不可修复产品，常用分布模型包括：指数分布、正态分布、威布尔分布与对数正态分布等，其中，威布尔分布被广泛地运用于可靠性工程及用户现场可靠性评估中。廖小波[2]采用两重威布尔分段模型对加工中心故障率浴盆曲线进行定量化建模；张根保、杨毅等[3]选用两参数混合威布尔模型进行数控折弯机故障数据建模，采用最大期望值（EM）算法进行参数估计；Wang、J Yang 和 G Wang[4]等提出了三参数威布尔混合模型，用于多个故障模式和原因的多个数控机床失效数据的建模。常用两参数威布尔分布的概率密度函数为：

步骤3 如果|Δtk+1-Δtk|≤ε3,输出值Δtk+1同时停止迭代;如果|Δtk+1-Δtk|>ε3,同时迭代次数k不大于最大迭代次数N,则跳转到步骤2;如果k大于N,停止迭代。

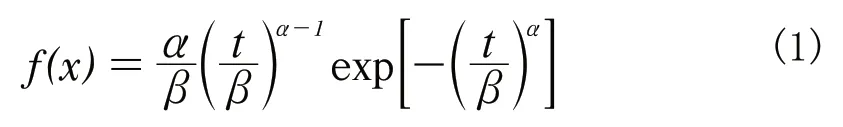
式中，α为形状参数；β为尺度参数。

3.2.2 随机过程分析法

当前，随机过程理论在可修系统可靠性评估中的应用是研究的热点，典型过程包括：齐次泊松过程、更新过程、非齐次泊松过程与不完全维修系统。王智明、张根保等[5]提出了基于随机点过程的多台NC机床时间截尾可靠性评估的可修系统，建立了故障时间的非齐次泊松过程（NHPP）模型；张根保、刘杰[6]提出了基于幂律过程的可靠性评估方法，基于Delta法进行可靠性指标的区间估计；张根保、李东英等[7]提出了基于对数线性比例强度模型的数控机床不完全维修可靠性评估方法；张根保、刘杰等[8]提出了基于广义比例强度模型的数控机床不完全维修可靠性评估方法。刘杰[9]研究了Kijima型广义更新过程在机床可靠性评估应用，采用非线性规划的方法对Kijima模型I&II参数进行了求解。

3.2.3 小子样下数控机床可靠性评估方法

数据的“小子样”是数控机床可靠性数据的一大特点，也就是说不能用常用的极大似然估计方法实现准确的可靠性评估。常用的小子样可靠性评估办法归纳有：

(1)对可靠性数据扩充，使用大样本下的经典方法或随机过程法进行可靠性分析，还可以利用非参数、参数及半参数Bootstrap方法估计可靠性模型参数及指标[10]。钱宝明[11]提出应用径向基函数神经网络对加工中心可靠性数据进行扩充，选择了合适的可靠性分布模型。张根保、刘杰等[5]融合多台机床的故障数据，提出CBT与CLT的分布检验法，解决了基于幂律过程的多台数控机床故障数据同质性验证问题。

(2)基于可靠性分布模型，利用Bayes方法充分融合各种先验信息确定先验分布（Bayes方法的重点），然后确定后验分布。如：刘杰[9]利用Bayes与Gibbs抽样方法解决了数控机床小样本数据下最小维修的幂律过程参数估计问题。

3.3 模型的假设检验

分布的假设检验是通过产品的寿命试验数据来推断产品的寿命分布，推断的主要方法是拟合优度检验法。拟合优度是观测值的分布与先验分布或拟合观测值的理论分布之间符合程度的度量。检验方法包括作图法与解析法，后者较前者更精确、更常用。解析法中的检验分布有 检验法、K-S检验法、Cramér-von Mises方法、相关系数检验法、似然比检验法、F检验法等。有些方法通用性强，有些方法只适合于某种情况。常用拟合优度检验方法如表1所示：

设参数β程序参数为paramst2与ests2，形式同上。

(2)利用Bootstrap分位数法计算 的区间估计；

(3)计算可靠性指标点估计与区间估计；

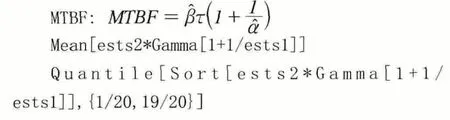
下面各表达式依次代入即可：

(4)运行结果如表3所示。

从表3中可以看出随着抽样次数B的增加，函数的极大估计值增大，参数的区间估计精度提高，因此选择B=1 000次的抽样计算结果，且K-S检验p=0.953＞0.05，表明该模型是有效的。

表3 威布尔模型参数估计(p=0.05)

表4 可靠性指标区间估计（t=1 000 h）

从表4的计算结果可以看出，在t=1 000 h处，该机床整体的可靠性水平较低，应该采取一定的措施降低故障率，尤其是早期故障消除技术，从而实现可靠性的可靠性增长。

5 结语

可靠性评估贯穿了数控机床的全寿命周期，是实现可靠性增长的关键技术。本文介绍了可靠性评估的定义、目的及意义、评估框架、评估流程和主要方法，值得注意的是数控机床的可靠性评估往往具有小子样特性，需要借助Bayes、Bootstrap等小子样方法对故障数据进行统计分析，最后通过实例分析了某型号数控机床使用阶段的可靠性水平。

[1]张根保,王立平.国产数控机床可靠性技术综述[J].航空制造技术,2013(5):26-31.

[2]廖小波.机床故障率浴盆曲线定量化建模及应用研究[D].重庆:重庆大学,2010.

[3]张根保，杨毅，刘杰，等.基于混合威布尔分布的数控折弯机可靠性评估[J].锻压技术2012，38(6):76-79.

[4]Wang Zhiming,Yang Jianguo,Wang Guoqiang,et al.Application of 3-parameter Weibull mixture model for reliability assessment of NC machine tools:a case study[J].Proceedings of the Institution of Mechanical Engineers,Part C,Journal of Mechanical Engineering Science,2011,225(11):2718-2726.

[5]王智明,杨建国,王国强,等.多台数控机床最小维修的可靠性评估[J].哈尔滨工业大学学报,2011,43(7):127-130.

[6]张根保,刘杰,杨毅,等,面向最小维修的数控机床可靠性评[J].机床与液压,2014,42(5):180-184.

[7]张根保,李冬英,刘杰,等.面向不完全维修的数控机床可靠性评估[J].机械工程学报,2013,49(23)：136-141.

[8]张根保,刘杰,高琦樑,等.多台数控机床不完全维修的可靠性评估[J].重庆大学学报,2014.37(2):1-6.

[9]刘杰.基于维修质量的数控机床可靠性评估技术[D].重庆:重庆大学，2013.

[10]陈文华,李奇志,张为鄂.产品可靠性的Bootstrap区间估计方法[J].2003,39(6):106-109.

[11]钱宝明.加工中心及其功能部件可靠性评估方法研究[D].重庆:重庆大学,2013.

[12]赵宇,杨军,马小兵.可靠性数据分析教程[M].北京:北京航空航天大学出版社,2009.

[13]杨建国,王智明,王国强,等.数控机床可靠性指标的似然比检验区间估计[J].2014,48(2):9-22.

[14]王智明,杨建国,王国强,等.多台数控机床的时间截尾可靠性评估[J].哈尔滨工业大学学报,2011,43(3):85-89.