地应力主要测试和估算方法回顾与展望
王成虎
中国地震局地壳应力研究所(地壳动力学重点实验室), 北京, 100085
内容提要: 随着人类对深部矿产资源和能源材料的需求量持续增长,深部开采问题必将成为工程界所面临的重大问题,而地应力参数的准确确定是有效解决该重大问题的基础工作之一。文章总结了目前在能源和资源开采中使用较为广泛的26种地应力测试方法,并对这些方法的基本力学原理、发展史作了简要介绍。这26种方法按照数据源途径可以分为5大类,分别为基于岩芯的方法、基于钻孔的方法、地质学方法、地球物理学方法以及基于地下空间的方法。这些方法依据满足工作需要的角度又可以分为主动法和现象分析法,对于社会基础设施建设、深部能源和资源开发,主动法的适用范围更广。不同的方法所反应的应力信息是不同的,相对而言建立在大体量岩体上的方法对于分析区域应力场更为可靠。最后文章对未来的应力测量与估算的发展远景进行了展望。
蓄存在岩体内部未受到扰动的应力称之为地应力(geo-stress 或 in-situ stress),地应力可以分为两类,原地应力和诱发应力(Amadei and Stephansson,1997),而原地应力主要来自五个方面:岩体自重、地质构造活动、万有引力、封闭应力和外部荷载(Amadei and Stephansson,1997;孙叶,1989;陈宗基,1982)。地应力具有多来源性且受到多种因素的影响,因此地壳岩体地应力分布复杂多变。从海姆假说认为“岩体中赋存的应力近似为静水压力状态,且等于上覆岩体自重”到金尼克假说认为“垂直应力等于上覆岩体自重,水平应力等于岩体泊松效应产生的应力”,人们对岩体应力的认识逐步提高,并利用实测数据否定了以上两种假说。社会发展的需求直接催生了大量地应力测试和估算方法,而这些方法的发展又进一步促进了人类社会的基础设施建设、资源和能源开发。随着人类对能源和矿产资源需求量的增加和开采强度的不断加大,浅部矿产资源日益减少,国内外矿山都相继进入深部资源开发状态,而深部开采中遇到的“三高”问题(高地应力、高地温、高水压)将成为深部开采岩体力学研究中的焦点和难点问题(何满潮等,2005)。准确确定深部开发空间区域的原地应力状态是解决以上难题的必要途径之一,这就需要进行地应力测试方法和技术的研究。
实际上深部地壳应力状态的观测与估算也是地应力实测工作的一个重要难点问题,因此非常有必要对现有的测试和估算方法进行一个全面梳理。Haimson(2010)曾指处任何地应力测试方法都有其局限性,确定一个区域的应力状态最好是利用多方法综合确定。从地应力概念提出至今,各国科学家提出了数十种地应力测试方法,将其按照数据来源进行归类,大概可以分为五大类:基于岩芯的方法、基于钻孔的方法、地质学方法、地球物理方法(或地震学方法)、基于地下空间的方法(Hill et al.,1994;Amadei and Stephasson,1997)。下面将对各种方法的测试原理和方法发展的脉络作一些简要介绍,供有关科研技术人员参考使用。
虽然表1包括了目前认可程度和使用范围较广的各种方法,还是有一些非主流的方法没有收录到表1内,其中Zang和Stephasson(2010)还对应力测量的物理学方法进行了回顾介绍,但是由于其在岩石力学、能源开发领域中应用较少,故在这里不作介绍。下面将对表1中的主要方法进行详细介绍,对于从这些主要方法中衍生出来的方法均只作一般性介绍。
1 基于岩芯的方法
这里提到的所有基于岩芯的方法都需要使用定向岩芯。因此采取质量良好的定向岩芯是开展下列测试工作的首要和必要条件。当然,也可以使用其它方法来确定岩芯的方向,例如测量岩芯所携带的地磁信息来确定岩芯的方向,但是测量精度会影响后面的测量结果。
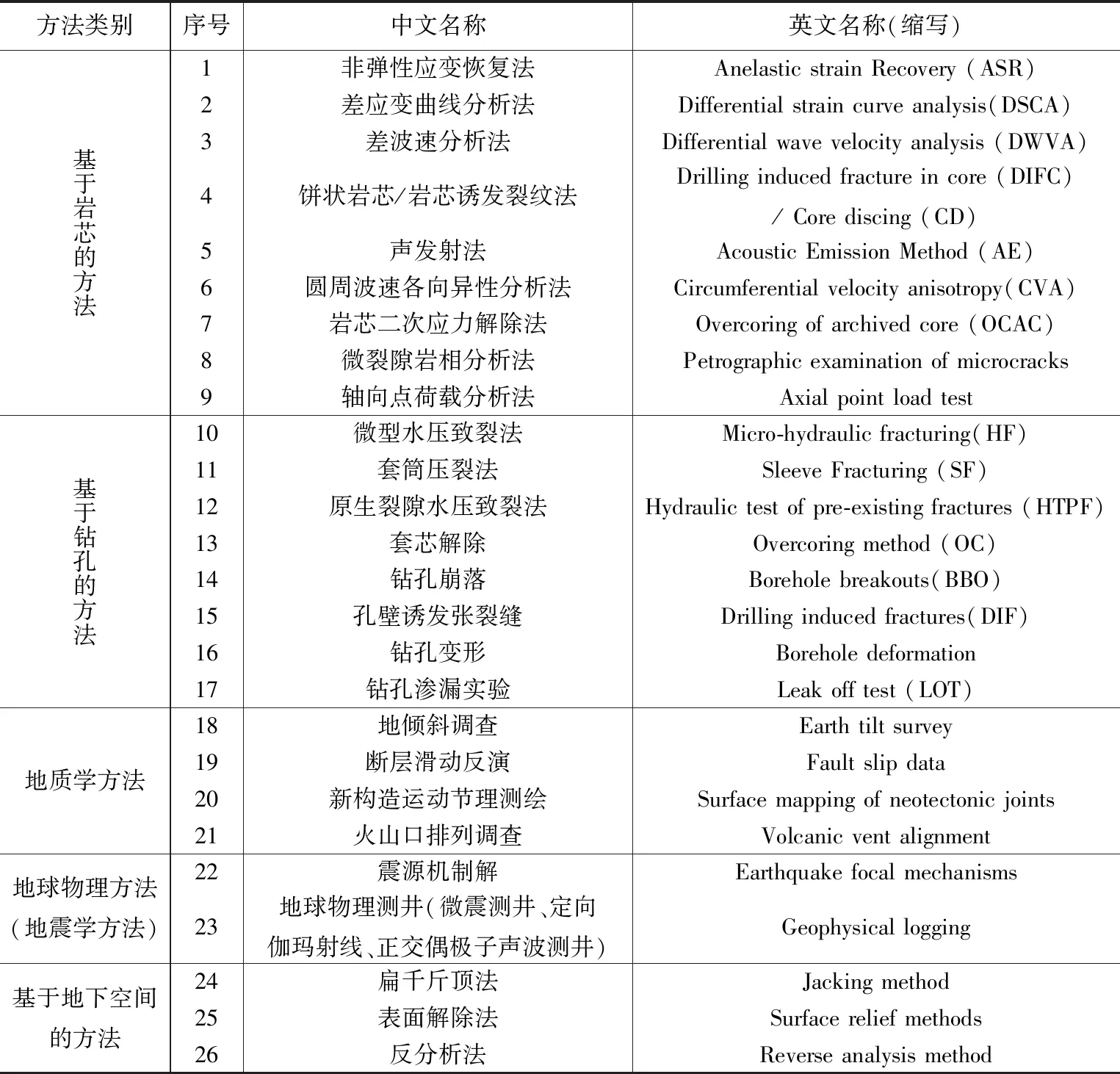
表1 原地应力测试和估算方法汇总Table 1 Summary of in-situ stress estimate methods
注:据Hill et al.,1994;Amadei and Stephasson,1997;Bloch,1999;Zang and Stephasson, 2010。
1.1 非弹性应变恢复法
非弹性应变恢复法(ASR)是通过测量现场从井孔取得的定向岩芯与时间相关的应变松弛变形来反演原地应力场方向和量值的一种方法。岩芯从井孔取出后,由于作用在岩芯上的原地应力场突然消失,岩芯会沿周向产生差别松弛变形,变形包括岩芯从母岩解除下来后立即产生的弹性变形和随岩芯放置时间延长逐步产生的非弹性变形。Voight(1968)建议使用经验修正考虑恢复的非弹性应变与全部恢复应变(包括弹性和非弹性两类应变)的正比关系以及相应的与先前的应力状态的正比关系。Teufel(1983)实现了Voight(1968)的想法,他发明制作了一个可靠且实用的能确定深部地层原地应力方向和量值的设备。Teufel(1983)认为应变恢复过程实际上是微裂隙形成的结果。非弹性应变恢复过程原理如图1所示(Teufel,1982, 1983, 1989, 1993)。这些变形都与原来加载在岩芯上的原地应力场密切相关,因而可以通过测量这些变形量来分析原地应力场。利用ASR测量数据确定原地应力量值相对于确定应力方位更加困难,需要建立一个岩样松弛过程的模型。Blanton(1983)建立了一个零阶模型,适用于各向同性和横向各向同性岩芯材料,利用这个模型就可以计算应变松弛过程中任何时间点上主应变的相对应力量值。Warpinski和Teufel(1986)在进一步提出的一阶蠕变模型中使用两个独立蠕变柔度,一个用于表示岩石变形体积膨胀,另一个用于表示岩石变形形状畸变。Matsuki(1991)发展了二阶蠕变模型,将二维平面应力分析拓展到了三维应力分析,应力分析中使用六个独立的ASR法向应变测值来进行应力计算。然而仅报道过有限的三维应力分析模型的应用实例(Matsuki and Takeuchi,1993;Ito et al.,1997;Lin et al., 2006b,c,2007a)。
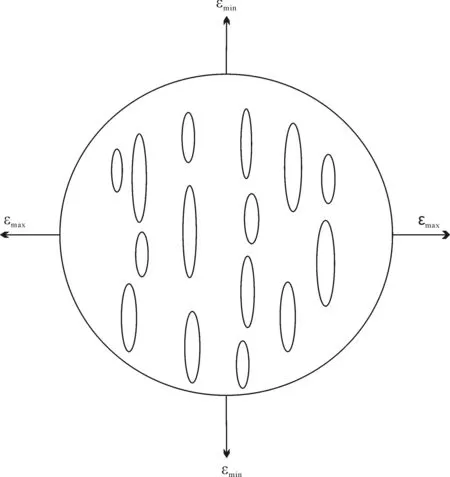
图1 非弹性应变恢复法原理示意图 (Amadei and Stephasson, 1997)Fig. 1 Principal behind the anelastic strain recovery (Amadei and Stephasson, 1997)
目前可以通过两种方法测试岩芯的非弹性应变量,一种是高精度卡夹(Teufel,1982, 1984, 1989, 1993;Wolter and Berckhemer, 1989),一种是应变片(Lin Weiren et al.,2006, 2010)。

图2 DSCA法测试原理及岩样差应变曲线示意图 (Amadei and Stephasson, 1997) (a) DSCA法测试原理; (b) 岩样差应变曲线示意Fig. 2 Principal behind the DSCA method and schematic of differential strain behavior (Amadei and Stephasson, 1997) (a) Principles of DSCA method; (b) schematic curve of differential strain behavior
ASR法会受到测试温度、岩芯脱水作用、岩芯孔隙水压扩散作用、岩芯不均匀松弛变形、岩芯各向异性、钻探水岩反应、残余应变、岩芯采取时间及岩芯定向不准等因素的影响(Teufel,1993)。因此在使用该方法时,在保证应变测试质量的同时,也应该对影响因素的作用程度进行深入分析(Zang and Stephasson,2010)。该方法主要适用于深孔和软岩的岩芯应力测量,当岩芯从深孔中取出后,由于原来经受的应力很高,非弹性应变恢复现象会非常明显,对于浅孔和硬岩,由于非弹性应变量较小,使得测试结果的可靠性降低。
1.2 差应变曲线分析法
差应变曲线分析法(DSCA)是在实验室内对定向岩样施加围压,观测比较岩样不同方向上的相对应变,进而估算原地应力方向和量值(Simmons and Ritcher, 1974; Simmons, et al., 1974; Siefried and Simmons, 1978)。DSCA法基于四个重要假设:① 岩样内部的微裂隙是由于岩芯围压消失而产生松弛变形所导致的;②微裂隙基本按照原始应力场的方向排列;③任何方向上微裂隙所产生的体积变化与原地应力场量值成正比;④ 在静水围压作用下,任一特定方向上的岩样体积收缩与该方向上的岩芯从母岩上解除下来的应力松弛变形过程是可类比的。在均匀的围压作用下,岩芯不同方向产生的应变是完全不同的,如微裂隙闭合,而这种应变信息可以用来分析原地应力场,测试原理如图2(a)所示。在20世纪70年代,Simmons and Ricther (1974)、 Simmons等(1974)、Strickland等(1979)在实验室验证了岩芯样品内部的微裂隙是钻探过程中由于岩芯松弛变形所产生的结果。基于这些观测结果,Strickland and Ren(1980)对DSCA法进行了修正,将其用于预测原地应力。后来Ren和Roegiers(1983)利用定向岩芯进一步验证了利用DSCA观测原地应力的有效性和可靠性,并认为这种方法是一种非常经济实用的方法。Thiercelin等(1986)对DSCA法进行了改进,并将其用于美国科罗拉多皮申斯盆地的多井实验场地的应力场确定。
图2(b)是岩样在均匀静水围压作用下的应变响应曲线。当施加的围压应力较低时,由于岩样内部存在的张开微裂隙或者半张开微裂隙,岩样表现出高度柔性。随着围压逐步增加,微裂隙开始全部闭合(转换区),过了转换区后,仅有岩样本体的弹性变形。实际上,实验应力-应变曲线的起始段范围内,包括两部分应变量,微裂隙闭合的应变表现和岩样本体的应变,岩样本体的应变可以通过高压段的应变曲线观测获得,在起始段范围内将岩样本体应变剔除,就可以计算出微裂隙闭合所反映的应变量。当然,如果岩样均匀且各向异性,那么可以不必考虑岩样本体的应变。利用DSCA的应变记录曲线可以直接得到原地应力场的方向和三个主应力之比,应力量值还需要通过其它一些假设或者测试数据再结合主应力之比来确定。DSCA法测试的立方体样品准备及测试设备组成参见图3所示。

图3 DSCA法测试样品准备及测试设备示意图: (a)试样立方块应变计布设方式; (b)测试设备组成示意 (根据及川寧己等, 1995)Fig. 3 Schematic drawing for preparation of test cube and equipment of DSCA method: (a) layout modes of strain gauges on a test cube; (b) components of test equipment for DSCA method (According to Oikawa et al., 1995)
但是实际上应力松弛变形过程是不可逆的,已有很多实验证明了这点(Ren and Roegiers,1983;Zang and Stephasson,2010),在实验过程中也需要注意与ASR法类似的影响因素问题。但是该方法在很多应用条件下仍然能提供很好的测量结果。该方法的优点是可以不考虑岩芯放置时间对实验结果的影响,这一点可以大大弥补ASR法的不足,并可以与非弹性应变恢复法配对使用。该方法的适用范围与ASR法类似。
1.3 差波速分析法
差波速分析法(DWVA)与差应变曲线分析法所遵循的基本原理一致,但是差波速分析法是沿岩样周边测量声波速度。对不同测点(不同方位)上在不同应力状态下的声波速度进行测试比较分析,就可以对原地应力状态进行估算。该方法只能给出地应力方向,不能给出应力量值。该方法的适用范围与DSCA法类似。
1.4 圆周波速各向异性分析法

图4 岩芯微裂隙效应的示意图 (Hill et al.,1994,有修改)Fig. 4 Schematic of micro-crack effects (After Hill et al., 1994, modified )
圆周波速各向异性分析法(CVA)可以用来确定应力方位并分析岩芯内部结构。由于岩芯内部的微裂隙一般会成组定向分布,如图4所示,因此沿岩芯圆周的波速分布呈现出各向异性特征(Hill et al.,1994)。如图5所示,岩芯圆周波速会随测试位置的不同而发生变化,因为每个测试方向所穿过微裂隙数目会不完全相同。在测试过程中,一般会沿着岩芯圆周按照固定角度间隔测试多个点的声波速度,通常最大主应力方向上所产生的张开微裂隙最多,故岩芯波速最低的方位即为最大主应力方向。如果能进一步比较分析岩芯声波速度分布的理论曲线和实测曲线之间的差异(Sayers, 1988),将能揭示更多关于测试岩芯的信息,理论拟合公式参见下式。
V(θ)=Vavg+Acos(2θ+α)+Bcos(4θ+α)
(1)
式中,Vavg是平均声波速度,θ是相位角,α是偏差角。
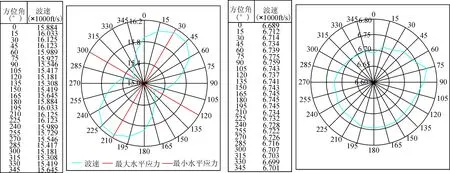
图5 CVA法测试结果示意图: (a) 好的CVA 法测试结果; (b) 差的CVA法测试结果Fig. 5 Some measurement examples for CVA method (a) Good measurements for CVA method (b) Poor measurements for CVA method
在实际测试过程中,有很多因素会给CVA测试带来困难。例如有些岩石内部很难发育微裂隙,有时微裂隙或许被其它因素所掩盖或者微裂隙对声波速度影响很小,那么波速各向异性就很小了。最好的例子就是高孔隙率岩石,微裂隙对声波速度各向异性影响很小。当测点声波速度差异小于2%~3%时,推算的应力方向认为是不可靠的。第二个比较大的因素是岩石结构对速度各向异性的影响,然而岩石结构的波速特征与微裂隙完全不同,特别是利用理论模型和实测数据进行拟合对比分析时,这种差异更为明显,而且这种差异也能为岩石结构研究提供定量分析数据。图5就展示了一个良好的CVA测试结果和一个不好的CVA测试结果,同时也给出了测试时所需要依据的测点布设原则。
CVA方法的好处是如果能拿到定向岩芯,可以在任何时候开展,即使是存放时间很久的岩芯,有时也能得到很好的测试结果。与此同时,CVA是一种无损测试方法,因此可以在各种岩样上开展实验而取得丰富的数据。故CVA方法也能作为ASR或者DSCA/DWVA方法一种补充或者验证方法。
1.5 饼状岩芯/岩芯诱发裂纹法
在高应力区开展钻孔施工时,岩芯经常呈现为薄饼状或者片状,大多数情况下,这些岩芯呈马鞍状,有时岩芯顶面和底面也相互平行,人们一般把这种现象称之为饼状岩芯。众多研究成果显示,这种饼状岩芯主要是由于当最小主应力方向和岩芯轴线方向平行时钻孔取芯过程中产生的张应力造成的(Jaeger and Cook,1963; Sugawara et al., 1978; Haimson and Lee,1995; Haimson,1997; Matsuki et al., 1997; Li and Schmitt, 1998)。一般饼状岩芯均出现在深孔钻探过程中,因此可以利用该现象提取应力信息。饼状岩芯的形态可以给出最大主应力和中间主应力方向,如图6所示,饼状岩芯的鞍状凹面轴线方向即为最大主应力方向,与轴线方向垂直的方向为中间主应力方向(Haimson and Lee, 1995; Haimson, 1997, Matsuki, et al., 1997; Li and Schmitt, 1998)。
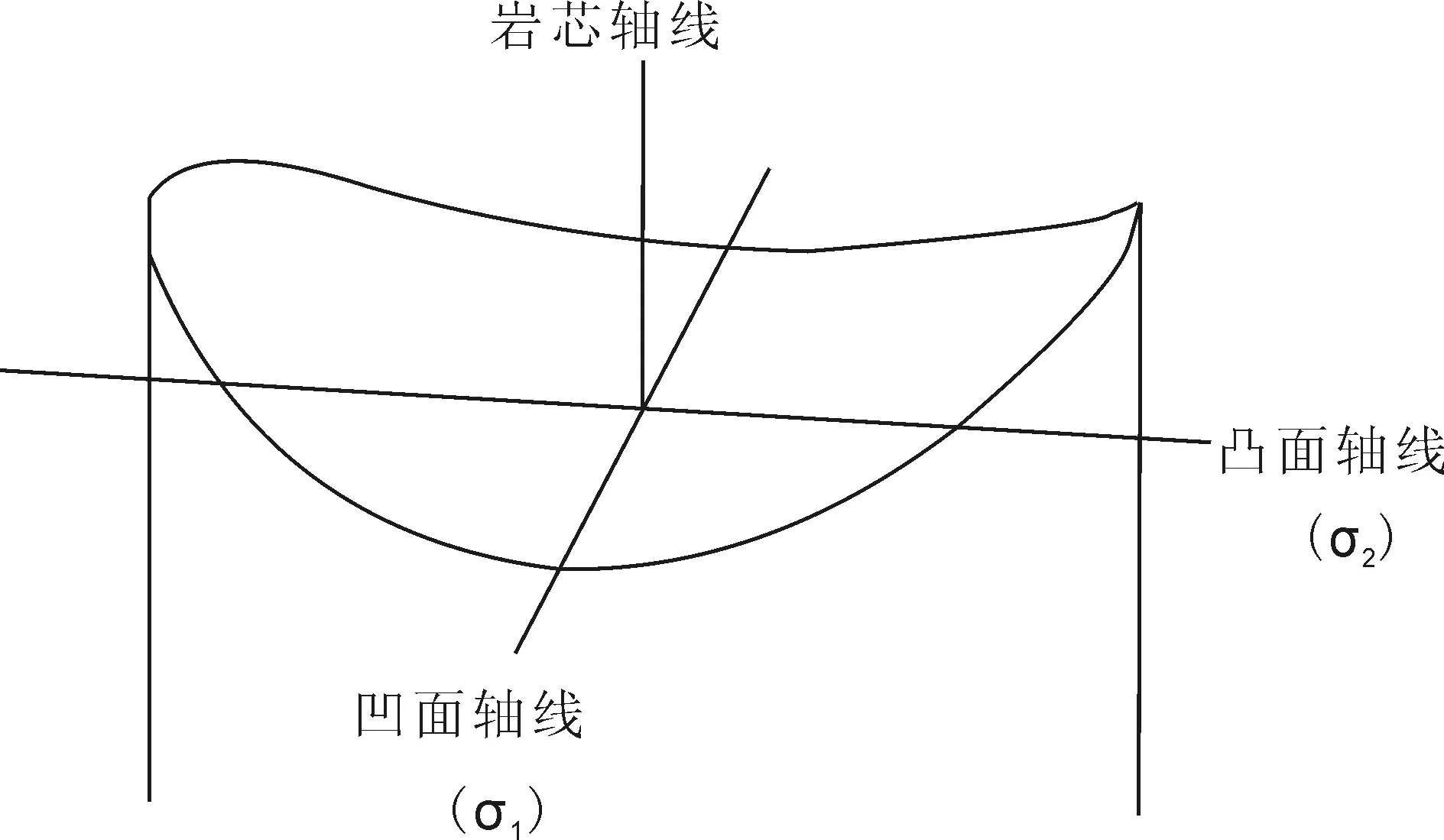
图6 饼状岩芯鞍状断面以及最大和中间 主应力方向示意 (根据Matsuki, 2004)Fig. 6 A saddle-shaped end surface of a disc with orientations of the maximum and intermediate principal stresses (According to Matsuki, 2004)
饼状岩芯也可以用于分析原地应力场的量值。针对与饼状岩芯现象有关的应力估算问题,Obert and Stephenson (1965)开展了大量的室内钻探模拟实验,通过对实验结果的分析总结,他们得到了饼状岩芯发生时的应力条件经验公式:
σr=k1+k2σz
(2)
式中,k2的范围为0.59~0.89,取决于岩石情况,k1为岩石抗拉强度的6.5~10.5倍,可以用巴西盘实验确定。他们的实验结果同样也给出在围压和轴压的高应力组合条件下能产生比地应力组合更薄的岩饼,但是这些均只是给出了定性的分析结论。Sugawara等(1978)提出了发生饼状岩芯的准则,Matsuki 等(1997)则提出了长岩芯发生饼化的准则。然而,这些研究并没有定量考虑应力量值对岩饼厚度的影响,但是Haimson 和 Lee(1995)、Haimson(1997)的实验室研究结果清楚的显示出岩饼的厚度取决于应力量值。因此目前饼状岩芯只能被用作定性估算二维平面应力状态(Ljunggren et al., 2003)。另外,认真仔细测量岩饼的尺寸显示对于给定的σh和σV,岩饼的厚度随着σH的增加而单调递减,如图7所示。这一结果表明如果定向岩芯岩饼的厚度与最大水平应力之间的关系建立了,那么最大水平主应力量值和方向可以分别通过岩饼的平均厚度和马鞍槽轴线方向来确定。Haimson等(1997)也同样指出可以通过测量岩饼的特征尺寸来估算原地应力水平的上限。基于数值模拟分析结论,Hakala(1999)给出了利用饼状岩芯现象分析解释原地应力状态的方法,在分析过程中最低需要以下信息:① 岩石抗拉强度;② 岩石泊松比;③ 岩石单轴抗压强度;④ 岩饼平均间距;⑤ 岩芯裂缝形态;⑥ 岩芯中的裂缝发育程度。

图7 当给定σh 和σV时,岩饼厚度td(利用岩芯直径D 进行归一化处理)与σH之间的关系(Haimson,1997)Fig. 7 Example of relation between disc thickness td (normalized by core diameter D) and σH for given σh and σV (Haimson, 1997)
在实践中,饼状岩芯现象只能被用作估算岩芯应力状态的一个指标。当出现该种现象时,我们当然可以认为岩石应力集中超过了岩石强度。这样的类似信息在钻探阶段取得,当然对后续的应力确定非常宝贵,也可指导后续应力确定和估算策略的选取。但是由于饼状岩芯出现的几率是非常低的,因此其使用机会非常少。另外,饼状岩芯的定向和岩石力学参数取得非常困难,这就制约了其在实践中的应用范围。鉴于以上原因,饼状岩芯所产出的应力信息可靠性相对较低。

图8 岩芯花瓣状裂纹形成的力学示意图(根据Lorenz et al.,1990): (a) 岩芯钻头前部的 主应力迹线分布示意图; (b)花瓣状裂纹的形成与三向主应力关系示意图Fig. 8 Mechanical schematic of formation of petal fractures in a core: (a) trajectories of principal stresses before the drilling bit; (b) the relationship between the formation of petal fractures and three principal stresses (According to Lorenz et al., 1990)
不同的应力条件下开展钻探取芯,钻探过程会对岩芯产生不同的作用效果。上面提到的饼状岩芯只是其中的一种现象。在有些情况下,会在岩芯上产生花瓣状裂纹或者中心线花瓣裂纹。通常花瓣状裂纹均匀分布,从岩芯外沿向岩芯中心延伸,花瓣状裂纹弯曲方向与岩芯轴线平行。中心线花瓣裂纹一般会延伸至岩芯的中心部位或者接近岩芯中心的部位,并沿与钻孔轴线或者平行于钻孔轴线延伸传播一段距离。Kulander等(1979、1990)认为这两种裂纹均是由于钻头钻进产生的诱发应力场和原地应力场叠加而在钻头前方的岩芯中形成。花瓣状裂纹的几何形状平行于钻头下部的主应力迹线,如图8a所示。花瓣状裂纹沿σ1和σ2所定义的平面(与σ3垂直)发展,其中σ1是垂直应力、钻头自重和液压加载应力之和,σ2是原位最大水平应力,σ3为原位最小水平应力,花瓣状裂纹形成的力学示意图如图8a所示。因此花瓣状裂纹走向与原地应力场最大水平主压应力方向一致(Kulander et al.,1979;Kulander et al.,1990;Li and Schimitt,1998)。花瓣状裂纹间距通常大于饼状岩芯的厚度,裂纹间距有时呈现出均匀分布,有时呈现出随意分布,这主要与原地应力状态、岩体性状以及钻探过程有关。Chang(1978)测量统计了大量的花瓣状裂纹,发现岩芯表面裂纹倾角一般在30°~45°之间。中心线花瓣状裂纹是花瓣状裂纹的特殊类型,Kulander 等(1979)将裂纹形态分为两个部分,起始段裂纹倾角从30°增加到75°,第二段裂纹则接近垂直,与图8a中的应力迹线类似。Li和Schmitt(1998)曾开展了大量的数值模拟研究分析原地应力场对岩芯诱发裂纹的影响机理,他们发现在正断层和走滑断层应力状态下,容易出现花瓣状和中心线花瓣状裂纹现象,在逆冲断层应力状态下,容易出现饼状岩芯现象。
岩芯的诱发裂纹检测要求使用定向岩芯,获取花瓣状裂纹和中心线花瓣状裂纹的数据过程中需要认真仔细检查岩芯(Lorenz and Hill,1992;Lorenz,1993),并且认真记录花瓣状裂纹的规则间距和花瓣的形状特征(例如前面所说的倾向、倾角以及倾角变化等)。记录数据的异常值需与钻探地质志相对照,例如扭矩、贯入度等其它可能影响花瓣状裂纹的因素相对比。花瓣状裂纹的测量主要是测量岩芯上所形成的裂纹数据,并不需要特别专用的设备。饼状岩芯或者岩芯诱发裂纹法主要取决于这两种现象是否会出现,利用两种现象得到的应力方向相对较为准确,应力量值一般误差较大。
1.6 声发射法
凯瑟效应指有应力状态下的材料发射声波的现象,故也称之为声发射(AE),这种现象仅在所受应力超过样品所经受的最大应力时激发。在材料科学领域, Kaiser(约瑟夫·凯瑟,1950)是第一位描述受拉金属、岩石和木材材料的这种记忆效应的科学家。在岩石力学领域,Goodman(1963)测试了受压条件下的砂岩,而Kurita和Fujii(1979)测试了受压条件下的结晶岩石,通过他们的工作把凯瑟效应介绍到了该领域。图9中展示了理想的实验室凯瑟效应测试图。如果声发射(AE)现象明显发生时的压力(所谓的回放最大应力(RMS),Hughson和Crawford,1986)等于PMS(先前经受最大应力)(如图9中所示,RMS=PMS),那么记忆实验室封存应力的凯瑟效应(KE)现象就被完美地证实了。然而如果施加应力越来越接近岩石的破裂强度时(如图9a,第三循环),声发射(AE)现象明显发生时的压力水平会低于先前所施加的最大应力(如图9b所示,RMS 图9 原始岩芯在实验室内循环加载时的应力—时间曲线(a),第二和第三个加载循环过程中测量得到的声发射事件和时间或者加载应力关系曲线(b) (Zang 和 Stephasson, 2010)Fig. 9 Cyclic loading of a virgin rock core in the laboratory indicated by applied stress versus time curve (a), and a measured number of acoustic emissions versus time or applied stress in the second and third loading cycles (b) (Zang and Stephasson, 2010) 确定回放最大应力(RMS)并不是一个简单的工作,岩石声发射(AE)活动的启动时间点非常难确定。通常声发射(AE)启动点和结束点都被假设为加载压力等于回放最大压力(RMS)的点,可以通过累计AE事件—应力的曲线来确定。另外,AE曲线上的相对变化,即两个连续加载循环之间的AE事件数量或者AE发生率也可以用于进一步确定AE事件启动点(Yoshikawa and Mogi,1981,1989)。Lavrov(2003)就如何处理AE曲线并准确确定回放最大压力值(RMS)岩石中的凯瑟效应(KE)作了一个详细而全面的综述。先前最大应力(PMS)越接近岩石最终强度,那么凯瑟效应(KE)现象启动压力就越难确定。Li和Nordlund(1993)通过凯瑟效应(KE)实验证明了前面的结论,在开展试验时他们设定第一个加载循环的峰值压力接近于岩石抗压强度,在第二个单轴压缩循环中就发生FR效应。在Li和Nordlund(1993)等开展的岩石实验中,大部分岩石均显示出了良好的凯瑟效应(KE)行为(包括大理石、片麻岩、花岗岩、辉长岩、绿岩、斑岩、黄铜矿等)特征,但是基律纳(Kiruna)磁铁矿的FR值较低,显示出贫乏的凯瑟效应(KE)。 岩芯的二次应力解除法可以用于确定应力方向,也有可能用于确定应力量值。岩芯二次应力解除法的概念起始于测量岩石的残余应力(或者应变)。Friedman(1972)提出了沙粒在原位荷载的作用下发生变形并在胶结过程中封存残余应力的机理。Hoskins和Russel(1981)使用二次套芯解除技术测量了黑山地区岩芯的残余应变,发现结果与使用套芯应力解除在岩石露头上测得的结果较为一致。在取芯过程中,岩芯通过内部产生微裂隙以及形变释放掉了岩芯所存储的主要能量,但是岩芯内仍存在部分残余应力。成功地利用更小尺寸的应力解除过程也可以释放部分残余能量,这种能量变化可以通过残余应变的测量来获取。测试过程非常简单,在岩芯上粘贴应变花,然后进行二次取芯(Hill et al.,1994;Jaeger and Cook,1979)。在每个方向上在取芯前和取芯后的应变变化即反应了岩芯所存储的残余应变或应力。这种应变一般是与原地应力密切相关的。主应变方向可以通过应变花公式计算,如下所示。 (3) 存放岩芯的二次应力解除简便易行,并且非常方便用于各种存放岩芯上,因此其潜在的使用价值就十分明显。该方法有两个主要缺陷,第一是并不是所有的岩石都对二次解除呈现出明显的应力解除特性,第二是岩石结构在测量中会造成较大的误差。 对岩芯开展切片分析或者CT扫描分析非常有价值,这种分析不仅可以提供应力信息,也可以提供丰富的岩芯结构信息(Gies,1987)。过去通过光学显微镜来检测岩芯中的微结构信息,例如使用岩芯的薄片、光片、蓝色薄片或者荧光薄片来开展检测(Gies,1987;Soeder,1990)。但是目前岩芯的二维和三维CT技术已经非常成熟(康志勤等,2009),而且可以通过CT扫描数据实现数字岩芯建模(Hazlett,1997;Liang et al.,1998),更方便开展岩芯微裂隙的计算机统计分析。岩相检测分析通常可以区别应力松弛微裂隙和构造微裂隙。应力松弛微裂隙一般存在于晶粒间,宽度均一或者宽度沿某一方向单调变化。构造微裂隙有可能存在晶粒间也有可能切穿晶粒,宽度变化不稳定,特别是有些构造裂隙经历过溶蚀作用,更容易辨别。当然,经验丰富的检测人员完全可以区分各种微裂隙,因而岩芯的微裂隙岩相分析法完全可以用来确定应力方向和岩芯内部结构。这种方法可以作为其它基于岩芯的应力测试方法的一种补充,特别是在其它因素对测试数据影响较为明显时,用这种方法可以立即判定误差来源。 在传统方法下,可以将每个薄片的裂纹的方向记录,并绘制玫瑰花图,就可以得到微裂隙的优势分布方位;如果是CT扫描数据,那么可以通过计算机软件自动统计分析,并绘制玫瑰花图。如果这些微裂隙均被识别为应力/应变松弛微裂隙,那么就可以得到区域原位最大主应力方位,即垂直于微裂隙的优势分布方位。如果微裂隙并非应力/应变松弛裂隙,那么就无法通过这种方法得到应力信息,但是微裂隙的信息可以为其它基于岩芯的应力测试方法提供可靠的诊断数据。 定向岩芯的强度各向异性也可以用于确定地应力方向。这一概念首先由Logan和Teufel(1978)提出,他们使用点荷载手段和巴西盘实验对Wattenburg油田的岩样进行广泛实验发现岩石的强度各向异性与水压致裂裂缝方位密切相关。Laubach等(1992)曾利用点荷载实验确定地应力方向,同时还发现了岩样强度的双峰分布模式。点荷载测试是岩样强度各向异性中较为简单的测试方法。测试过程中,利用半球状压头对饼状岩样顶面和底面进行施压,直至岩样破坏。对岩样的破坏模式进行统计分析,得到岩石的微结构特征。如果微结构主要与松弛微裂隙有关,那么诱发破坏裂缝方位会与实验前的微裂隙分布方位一致,而这一方位与最大主应力垂直。如果微裂隙与构造微裂纹相关,那么诱发破坏裂缝方位与实验前的微裂隙分布方位一致,而这一方位不会与最大主应力方位是垂直相交。如同其它基于岩芯的测试方法一样,知道岩样的微结构特征对于准确测试非常重要。在点荷载测试中,要求准备的岩饼应该有相互平行的端面;如果为了得到最大水平应力,那么在岩饼的端面必须水平面内相互平行。在实验阶段,特别注意的是应该使用中等的加载速率以将动载效应降到最低。因此一般情况下,建议该方法和CVA法或者微裂隙岩相分析法联合使用。该方法非常大的困难是很难判断点荷载测试所产生的强度各向异性到底是由于应力松弛裂隙造成的,还是由于岩样本身的内部结构特征造成的;因此不建议单独依靠该方法对应力方向进行估算。该方法的优点是测试设备和技术简单便宜,开展大量测试方便快捷,因此在样品数量较大的情况下非常适合进行统计研究。 应力测量中的水压致裂法又称微型水压致裂法,微型是相对于油田压裂而言。在水压致裂技术提出之前,科学家们主要使用应力解除法来测定原地应力,包括平面应力解除法、钻孔套芯应力解除法、扁千斤顶法(平面应变恢复法)等。Hubbert和Willis于1957年提出井孔液体压裂所产生的裂缝与岩体中所赋存的应力状态密切相关,并指出岩体压力并非处于静水压力状态。Scheidgger(1962)是第一位利用油井孔底压力曲线分析地壳应力的科学家。Fairhurst(1964)是第一位提出利用水压致裂技术来测量原地应力的科学家,并指出了水压致裂技术的诸多优点。Haimson和Fairhurst(1967)指出井壁上产生的裂缝与以下三个因素有关,① 地壳应力,② 水压致裂的液体压力与孔隙水压力之间的差应力;③岩体渗透的径向流量,这些理论分析奠定了经典水压致裂测试技术的理论基础。Haimson(1968)在其博士论文中对水压致裂原地应力测试技术从实验和理论两个方面进行了全面分析和完善。以上这些重要工作为将水压致裂原地应力测试技术应用于工程实践奠定了理论和实验基础。真正意义的应力测量工程实践是由Von Schonfeldt 和Fairhurst(1970)领导的研究组在明尼苏达州的一个地下花岗岩岩体中展开的;随后,在Rangely油田也开展了类似的应力测量和研究工作(Haimson,1973;Raleigh et al.,1976)。从此,水压致裂应力测量正式进入工程实践领域。于1981年,加利福尼亚Monterey市召开了全球第一次水压致裂应力测量研讨会,水压致裂原地应力测试技术和方法逐渐被全球各行各业的科学家所认同。1987年和2003年,国际岩石力学学会都把水压致裂原地应力测量方法作为一种主要的应力测试或者估算方法来推荐,也奠定了水压致裂原地应力测量技术作为应力测试方法的重要地位。水压致裂的基本原理是利用一对封隔器在钻孔中隔离出一段试验段,然后用高压流体将试验段岩体压裂,产生竖直缝,同时记录压力-时间曲线,通过曲线来判断液体压力和原地应力的平衡点,进而得到原地应力状态。 1980年10月,由李方全教授领导的研究组在河北易县首次成功地进行了水压致裂法地应力测量(李方全等,1986),随后中国地震局地壳应力研究所研制成功轻便型水压致裂测量设备(谢富仁等,2003)。水压致裂测试技术开展在中国的各行各业得到广泛的应用推广。Kuriyagawa 和Kobayashi (1989)提出利用三个近似正交的钻孔开展水压致裂测试工作,可以计算测试区域的全应力张量;随后刘允芳(1991)将该方法介绍到中国,郭启良等(2004)则将该项测试技术推广到了地下工程领域。 水压致裂法测地应力的优点非常明显,对测试设备和测试环境的要求相对较低,测试过程简便迅速,数据处理分析也简便易行。但是水压致裂法也存在很多的问题,首先是最大水平主应力SH的计算受到较多因素的影响,如Ito(1999)等曾指出测试系统柔性对Pr的选取影响明显,进而会影响SH的计算;其次是在深孔测量时,一般系统柔性较大,而且岩体的渗透性也会对测试过程产生较大影响,同时深孔测量对水压致裂测试的井下设备提出了更高的要求。针对水压致裂测试系统的种种问题,Ito(2010)提出了BABHY测试系统,但是如何推广这种测试系统,仍然是工程师和科学家们所需面临的问题。 如前面所述,传统水压致裂测试中由于压裂液渗透的问题会对原地应力测量中的破裂压力发生影响。为了解决这一问题,Stephasson(1983b, c)提出了套筒压裂法,套筒压裂使用旁压仪的高容量薄膜对围压施加压力,当施加的压力超过岩石的抗拉强度,孔壁围岩上就会产生竖直裂缝,并且沿着垂直于最小水平主应力的方向传播。由于没有液体渗透进入孔壁围岩岩体,故可以直接通过破裂压力和重张压力获得原地最大最小水平主应力。Stephasson所提出的理论和设想实际是Hustrulid和Hustrulid(1975)所提出的柔性CSM旁压仪器的一个拓展。随后不久Ljunggren和Stephasson(1986)研发了刚性旁压系统。在套筒压裂测试中,水平应力量值通过记录的压力—容积曲线确定,应力方向通过缠绕在套筒表面的黑色乙烯基电绝缘带表面的裂缝印痕确定。套筒压裂提出后,随后还出现了一些其它类似的套筒压裂技术,例如Serata和Kikuchi(1986)和Serata等(1992)提出的双裂缝套筒压裂技术;以及Amadei等(1994)研发的ROCTEST系统;Li等(2005)所研发的千斤顶压裂系统。所有的这些套筒压裂技术都具备一个公认的优点,就是压裂过程中没有液体进入岩体,只要准确确定了破裂压力和重张压力,就可以得到岩体的抗拉强度,故得到的应力量值相对更为准确,同时由于压裂是通过压力膜或者其它压力顶加压,所以形成的裂纹一般为竖直裂缝,而且形状和长度可控。套筒压裂法的缺点也较为明显,非常难确定加压过程中的破裂压力和重张压力,而一些能准确确定破裂压力和重张压力的设备又非常复杂,在井下应用困难,这些缺点大大制约了套筒压裂技术的推广使用。 原生裂隙水压致裂法是利用一对封隔器在钻孔中隔离出一条闭合原生裂隙,利用高压流体将闭合原生裂隙张开,通过压力-时间曲线可以得到作用在裂隙面上的法向应力,完成在至少6个走向和倾角完全不同的闭合原生裂隙上的测试,就可以求解测试点的全应力张量值。Cornet(1984,1986)首次提出了利用钻孔所揭露的原生裂隙开展水压致裂测量来计算全应力张量的HTPF法。刘允芳(1999)则率先在国内将相似方法应用于工程实践。在国内原生裂隙水压致裂法测试方面,李方全(1986),刘允芳(2000),陈群策(1998)等学者都进行了实践,并取得了一些研究成果。Cornet(1997),刘亚群(2007),景锋(2009)等提出使用HTPF法时,当原生裂隙间垂直距离超过50m时,需要考虑应力梯度对其的影响。 原生裂隙水压致裂法(HTPF)优点很明显,测试过程只需要测试作用在闭合裂隙面上的法向应力和裂隙面方位角,不需要测试其它岩石力学参数,方法原理假设很少,测试过程和测试参数可靠。同时HTPF法中,仅有精度较高的关闭压力Ps参与计算,测量精度提高。HTPF法在实际计算中,由于测量过程中存在误差,仅以6段原生裂隙进行计算,有可能造成计算机计算无法收敛,所得到的各应力量值与实际值之间存在很大差距。在此,Cornet建议最少选用7段原生裂隙数据进行计算,选用8~9段各参数不同的原生裂隙数据计算,得到的结果可靠性较高。然而HTPF法测量过程较经典水压致裂法复杂许多,测量过程中需要对每条裂隙进行精确定位,且对原生裂隙的赋存状态要求很高。在同一个钻孔内寻找不同产状的原生裂隙难度非常高,根据王成虎等(2006)的钻孔电视测试结果可知,同一钻孔所揭露的原生裂隙产状均趋于优势方位。原生裂隙附近可能存在其他裂隙,对原生裂隙的封隔加压很难保证将该裂隙独立分隔开来;同时保证测量过程中没有液体渗入裂隙内亦很困难。 刘允芳(2006)进一步改良了原生裂隙水压致裂法,在原有基础上,提出裂隙重新张开时,裂隙面上剪应力应为0,那么每进行一段原生裂隙水压致裂测试,可获得3个观测值方程。只要在两个或两个以上不同产状的原生裂隙段上进行重张试验,即可确定三维地应力状态。仅以2段原生裂隙数据进行计算很难得到理想的数据,在此笔者建议利用4~5段原生裂隙数据进行计算较为妥当。 通过近些年的理论发展,HTPF法对裂隙赋存条件的依赖程度大大降低,由最开始需要至少6条原生裂隙到现在只需要2条原生裂隙就可以计算出三维应力状态。但是HTPF法在不断改良的过程中,也加入了一些新的假设,其测量精度还有待实践的进一步考验。 井孔内的钻孔崩落现象可以通过光学(照相机),机械式测井仪(井径仪),超声波测井仪(钻孔电视)或者电阻测井仪(地层微扫描器,简称FMS)观测。超声波钻孔电视(BHTV)能够提供井孔壁连续且定向的超声波图像(Zemanek et al.,1970)。当测井工具沿钻孔逐步上移时,BHTV能按照螺旋线的方式以细窄的脉冲式超声波射束扫描钻孔壁。高级设备如FMS(斯伦贝谢)能够产出高精度的钻孔壁电阻率图像,这种测井图像可以用于确定水压致裂裂缝、钻井诱发张裂缝和钻孔崩落方位。钻孔崩落可以帮助准确确定区域应力场方向,但是对于应力量值,需要针对钻孔围岩的强度、围岩的破裂条件进行相关测定和假设,进而限定应力量值的范围。钻孔崩落的应用依赖于该现象是否出现,一般在深度超过1000m的钻孔中,可以考虑采用该种方法,浅孔(<1000m)中该现象一般不会出现。 如前面所述,如果钻孔孔壁形成张应力集中或者钻井液压力过大,就会在钻孔孔壁上产生张裂缝。孔壁诱发裂缝走向一般与最大水平主应力方向一致,孔壁诱发张裂缝的基本原理与前面提到的水压致裂法类似。一般情况下,钻孔孔壁出现诱发张裂缝意味着①Sh是最小主应力;② 水平主应力SHmax与Shmin之间的差值很大(Zoback,2007)。有时候钻孔孔壁张裂缝也与高泥浆密度和钻孔孔壁冷却有关。地应力量值估算则需要结合钻井液参数、孔壁围岩强度属性的参数进行估算。孔壁诱发裂缝现象一般可在高应力区和深孔中观察到,孔壁诱发张裂缝一般均限制在距离井壁很近的范围内,穿透深度一般为几毫米或者几厘米(Brudy和Zoback,1999),可以利用前面所述图像测井技术(BHTV、FMS)以及一些其它精度较高的地球物理测井技术进行观测。井孔孔壁张裂缝的优缺点与钻孔崩落类似,属于一种现象分析的方法。 当钻孔孔壁的应力集中不足以导致岩壁破坏时,钻孔孔壁会产生一定程度的变形,钻孔变形是一种非常常见的现象,特别是超过特定深度后(>100m)。由于各种测试条件、要求和精度的问题,很多情况下,我们无法测试这一变形值。如果钻孔孔壁光滑规则,通过高精度的仪器还是能观测到钻孔变形程度,钻孔的长轴方向为最小水平主应力方向,短轴方向为最大水平主应力方向。而Zoback(2007)曾指出任何一个钻孔都可以看作我们在地壳岩体中开展的一次岩石力学实验,那么观察钻孔成型后钻孔围岩的响应特征将是这一实验的必要措施,故这种方法也是未来岩石应力测试的一个发展方向。Halliburton公司曾开发了THE(Total Halliburton Extensometer)设备来观测钻孔压裂期间钻孔变形情况,进而得到钻孔压裂期间的裂缝方位和孔壁位移情况,该设备包括一个或者两个封隔器和两套六臂线性测径仪(McMechan et al.,1992;Kuhlman et al.,1993)。Obara等提出了(2004,2010)CBDM(Cross-sectional Borehole Deformation Method)法来测定应力,并指出这种方法不仅可以测量初始原地应力也可以测量原地应力的绝对变化。Obara等(2004, 2010)研发出高精度的光学井下测试仪器来测定钻孔横截面变形,并用其估算原地应力值方向和量值。钻孔变形法目前仍在研发中,未来的推广应用情况仍然有待检验。目前能想到的该方法的问题包括:① 钻孔孔壁岩石的蠕变变形;② 在测试过程中消除由于钻探原因所造成的钻孔扩径现象;③ 如何将实验室岩石力学实验数据与钻孔孔壁的岩体数据建立联系? 钻孔渗漏实验测试地应力原理与微型水压致裂测试法原理相同,但是该方法主要在油田上使用较为广泛,通过渗漏实验的压力—时间曲线估算最小水平主应力 (Zoback,2007)。 地倾斜调查主要用于油田区域应力场分析,在进行油井压裂的过程中,地表会发生形变,地表的这种形变与地下的油井压裂裂缝扩散和分布密切相关。在油井区域的地表布置地表倾斜仪,通过测量地表形变及其分布特征,可以得到地下压裂裂缝的分布特征,进而得到区域应力场的方向特征(Hill et al.,1994)。一般情况下,这种地表倾斜仪的精度能够检测到水平距离400km长度上2mm的地表变形所产生的角度变化,或者更高的精度。理想条件下,需要在井下水压致裂前几个周就将地表倾斜仪埋入地下3~5m的预设孔内,一方面可以让仪器获得一定的稳定时间,另外一方面也可以得到研究区的环境背景地倾斜噪声,这种噪声包括日月潮汐,地表温度变化所产生的热弹性变形以及其它如风力、降水、地下水位变化、地表人类活动等所造成的地表变形。当基于钻孔或者基于岩芯的方法不能足以提供可靠的区域应力数据时,就可以开展这种地倾斜观测,但是压裂深度不能超过1500m,同时这种方法费时、花费高而且需要足够好的后勤保障。 地震预测研究中也使用了相应的跨断层地倾斜仪,常见的有水管仪(吴涛等,2010)、摆式倾斜仪(马武刚等,2012)和伸缩仪(杨江等,2010、2012),也可以在一定程度上反应中长期的地壳中的地应力场变化趋势,但是到目前为止仅见到利用其进行地震预报的报道,未见到相关的利用其进行反演区域应力场的报道,或许这在今后也是一项值得开展的研究工作,因为地震部门积累了大量的地形变观测资料。 图10 断层面上擦痕有关数据测量及计算的结果表示(侯明金和王永敏,2002)Fig. 10 Measurements of striations on fault planes and computation results expression (Hou Mingjin and Wang Yongmin, 2002) 该方法需要大量细致详实的野外调查工作,野外工作中最困难但也是最重要的就是确定擦痕的性质、滑动方向及断层活动期次配套,Mercier等(1992)曾对所采用的几类擦痕的判别方法进行了归纳总结,侯明金等(2002)对这些方法进行过简要介绍,可参考。对于人类活动稀少地区的区域应力场研究非常有价值,但是在断层擦痕露头不明显的地区,使用范围受限。该方法的一个很大的缺陷是非常难确定断层滑动擦痕发生的具体时间或者年代。 新构造运动节理测绘的统计结果可以估算新构造运动发生年代的区域应力场方向,其所基于的主要原理是安德森理论(Anderson,1951)。安德森理论认为主要的断层类型可以分为三类,正断层、走滑断层和逆断层,三种断层类型所对应的应力状态分别为SV>SH>Sh,SH>SV>Sh和SH>Sh>SV,而三种断层的走向与最大最小水平主应力的夹角也有一定的分布规律,这一统计规律就可以用来分析区域应力场方向(Zoback,2007)。拜尔利总结了众多岩石力学实验的结果,认为地壳岩石的内摩擦系数为0.6~0.85,少数岩石除外,这就是著名的拜尔利定律或拜尔利范围(Byerlee,1979)。其它一些研究成果表明,绝大多数岩石的摩擦系数在0.5~1.0之间(张伯崇、马元春,1987;李方全等,1993)。研究人员进行的原地应力实测证明实验室测得的摩擦系数适用于上地壳,且限定了上地壳的应力水平(Townend和Zoback,2000;Zoback et al.,2002;Scholz,2002)。由拜尔利定律可知,符合安德森理论的断层(以下简称安德森断层),中间主应力与断层面共面,当断层面上的摩擦系数为0.6~1.0之间,最大主应力与断层面的夹角较小,一般为23°~30°。 火山口排列调查法所依据的力学原理与水压致裂相似,但是这里压裂液为低粘度的熔岩岩浆,该方法由Nakamura所提出(1977)。Nakamura(1977)指出,所需要调查的参数包括: ① 火山口的形状(圆形或者椭圆形);② 火山口周边或者火山岩侵入围岩所形成岩脉的分布方式;③ 同期次火山口的排列方式;④ 火山附近的断层活动分布特征(展布和活动)。通常情况下,火山口排列或者岩浆岩岩脉的延伸方向与火山爆发时的区域最大水平主应力平行,与最小水平主应力垂直,如图16所示(Adiyaman et al.,1998),该方法对于古应力场分析研究非常有用。在实际运用该方法的过程中,需要仔细辨别不同期次火山形成过程的地质背景和构造条件、同时需要利用DEM或者遥感手段对火山口的地貌性态进行细致分析。该方法给出的古应力方向可靠度较高,但是对于一些古火山和复杂形态和多成因火山,需要开展更为细致的研究工作来确定形成时的古应力方向。 图11 地表火山裂隙出露形态示意及其与应力场方向的关系(Adiyaman et al.,1998)Fig. 11 Surface signatures of volcanic fissures, and their stress directions (modified from Adiyaman et al., 1998) 震源机制解的求解,主要是通过假定震源模型参数,计算得到给定地震波速度结构下各台站产生的波形特征,再将其与各台站实际观测波资料进行对比,得到拟合最好的模型参数。求解震源机制解的常用方法主要包括初动符号法和波形反演法,初动符号法主要依据波形的初动极性信息来获取震源机制解,而波形反演法则充分利用了波形资料求解矩张量解(Fowler, 1990)。初动符号法可分为P波初动法和振幅比法,通过判定初动符号极性获得震源机制解,其方法简单、快捷,但是从波形数据文件中获取的地震信息较少,需要大量台站数据资料,且只有在台站分布均匀的条件下才能得到可靠的结果。然而对于一些中小地震来说,由于受地震台站分布和密度的制约,用P波初动所求得的震源机制解有可能是不可靠的,因此许多学者提出了振幅比法,即根据P波与SV波或SH波振幅比值来求解震源机制参数(Kisslinger et al.,1981;梁尚鸿等,1984;吴大铭等,1989)。震源机制解研究中,通常利用地震矩张量来描述地震的点源模型,而地震矩张量的引进实现了震源参数的线性化。根据矩张量元素和格林函数之间的线性关系,简正振型、体波、面波、近震源记录等波形观测资料均可用于矩张量的反演(倪江川等,1991;祁玉萍等,2013)。目前,美国、日本、欧洲、我国台湾等都建立了实时波形自动反演系统,并将震源机制解的确定纳入了台网的日常工作(祁玉萍等,2013)。震源机制解能较为准确地得到地震发生时断层两盘的相对运动方向,这种相对运动方向反应了当时的区域应力状态,因而可以给出区域应力场方向和三个应力量值之间的比值关系(Zoback,2007)。 由于大多数地壳地震发生于原生的断层,而不是产生新断层而引发,所以滑动向量由断层方向、主应力方向和大小决定,而震源平面机制的P轴和T轴与主应力方向无直接对应的关系。Raleigh和Healy等(1972)建议如果已知震源机制的节平面,则不必采用震源平面机制的P轴,而假设最大水平主应力与断层面夹一定角度,而夹角大小可以根据摩擦系数来确定,比如,许多岩石的摩擦系数约为0.6,他们建议断层面与最大主应力方向的夹角可取为30°。但是对于板块内部地震,很难确定震源平面与哪个断层面相对应。尽管如此,在大多数内陆板块区域,震源平面机制的P轴仍然是最大水平主应力方向的一个较好的近似,这是因为内陆板块地震通常不是发生在摩擦系数很小的断层上(Zoback and Zoback,1980;Zoback et al.,1989)。 其它地球物理方法包括微震测井、定向伽玛射线和横波各向异性法。微震测井法主要用于油田应力场的研究,在油井压裂过程中,会产生微震事件,对这些微震事件进行精定位,并分析其分布特征,就可以得到压裂裂缝的分布特征,进而得到区域应力场方向(Hill et al.,1994;Zoback,2007)。其它的物理测井方法包括定向伽玛射线录井,横波各向异性法等。伽玛射线录井是一种在石油工业中常用的方法,定向伽玛射线录井基于常见的伽玛录井技术,并结合一些示踪元素来获得油井压裂过程中所形成的裂缝方位(Hill et al.,1994),进而得到区域最大主应力方向。横波各向异性是指在各向异性介质中横波偏振成快波和慢波两个分量,引起的机制可以分为两类,一类是主应力差异所引起的各向异性,另外一种是构造各向异性,其中应力各向异性情况下,垂向传播的弹性波在平行于张开的微裂缝(Crampin,1985)或者垂直于闭合的大裂缝(Boness and Zoback,2004)方向偏振为快速的方向,在这两种情况下,快速横波方向都平行于SHmax,基于这种原理,可以利用垂直井的正交偶极子声波测井资料的快速横波偏振方向确定应力方向,例如Yale(2003)就利用北海Scott油田某垂直井的交叉偶极子数据得到了横波速度各向异性,并确定了最大水平主应力方向。 地球物理测井方法确定区域应力场方向主要在石油工业中使用广泛,同时由于测井工作是油田储层分析的一项基础工作,因此应用广泛。但是由于地球物理方法多解性的问题,在使用地球物理测井方法开展相应的应力分析时,同时应该对其它影响因素予以考虑以提高获得应力数据的可靠性。 扁千斤顶法是测量岩壁表面应力的一种方法,也称岩体表面应力恢复法,该方法首先在二十世纪五十年代在法国使用,由Mayer等(1951)、Tincelin(1951)首先提出,后来Panek(1961)、Panek和Stock(1964)、Hoskins(1966)、Merrill等(1964)以及Rocha等(1966,1971)对这种方法又进行了大量的改进。到了20世纪60年代以后,文献中有大量关于利用扁千斤顶法测量原地应力场的报道(Amadei and Stephasson,1997)。该方法也是是国际岩石力学学会试验方法委员会岩石应力测量的推荐方法之一(Commission on testing methods of IRSM,1988)。首先在测量点按照特定规则埋设测量元件,一般埋设在预定测量槽的两侧,埋设完毕后,在预定位置开挖测量槽,同时监测测量元件所反应的开挖过程中岩体的变形行为(位移或应变量),再在槽中埋设压力钢枕,测量压力钢枕施压引起的变形,直至能抵消由凿槽引起的变形和该压力下的残余变形时,相对应的压力钢枕压力值就是窄缝槽中垂线方向的围岩法向应力值(Commission on testing methods of IRSM,1988)。当拓展到三维地应力测量时,一般需要在洞室断面岩壁上不同部位布置6个测点,测试设备及测点布置如图12所示。该方法在20世纪60年代时十分流行,到目前仍然有人在使用该方法。根据Amadei和Stephasson(1997)的介绍,从该种方法提出到20世纪60年代发展成熟后,除了在局部技术细节方面的部分革新,该方法后来的30多年里基本没有什么大的发展变化。与此同时,对该方法进行适当修正,还可以用于测试岩体的弹性模量。 图12 扁千斤顶法原地应力测量方法及测量槽布置示意图(Amadei and Stephasson, 1997) (a)扁千斤顶法原地应力测量方法示意图; (b)测量槽的布置示意图Fig. 12 Flat jack in-situ measuring technique and schematic for arrangements of measurement slots (a) Schematic of flat jack method (b) Schematic for arrangements of measurement slots (Amadei and Stephasson, 1997) 扁千斤顶法测量地应力有以下不足:① 该方法只能测量地下洞室围岩表面的地应力,而围岩表面的应力容易受到洞室开挖工艺、围岩二次应力场等因素的影响;② 围岩表面的结构面和岩体的各向异性对测试结果影响较大,而且不容易消除;③ 由于加载工艺的问题,千斤顶施加的应力不是理想均匀状态,同时应力加载过程与解除过程可能并不一致;④ 在一些软岩中开展实验时,切槽过程中的蠕变现象对测试结果影响明显。这种测试方法的优点也很明显: ① 可以直接测试地应力,而且无需知道岩石的弹性模量;② 测试设备简单、耐用、稳定;③ 所测得的应力是基于一个平面的平均应力,包括的体积达0.2~2m3,同时对岩体的扰动相对较小。 图13 三种主要表面应力解除法的测点和切割作业布置示意图(Amadei和Stephasson,1997; 康红普等,2013):(a) 小型岩体切割法; (b)平行钻孔法; (c)中心钻孔法Fig. 13 Schematic arrangements of measuring spots and cutting operations for three major surface relief methods: (a) small-scale cutting of rock mass; (b) Parallel borehole method; (c)Central borehole method (Amadei and Stephasson, 1997;Kang Hongpu, et al.,2013) 平面应力测量法是最早的应力测量方法,早在20世纪初就有工程师利用这种方法测量土木结构组件内部的应力。表面应力解除法是在测试点安装变形测量装置,一般采用几组固定的测量元件,成对按照特定形状规则固定,然后在测量元件周边开展岩体切割或者小型开挖作业,在这一过程中,监测测量元件之间距离的相对变化,进而得到开挖过程中测量点岩体的变形量,同时求得该区域岩体的弹性模量,就可以估算测量点原地应力状态。这种方法在应力测量发展的早期起到了很大的作用,近年来该方法的使用率已经很低了。Mathar(1934)、Amadei和Stephasson(1997)对表面应力测量进行过系统地总结,可参考。应力测量发展史上最为著名的表面应力测量工作是Lieurance(1933、1939)在美国内华达胡佛大坝坝基中所开展的应力测量实践。表面应力解除可以分为小型岩体切割法(Merrill,1964)、平行钻孔法(Habib,1971)和中心钻孔法(Duvall and Tsur-Lavie,1974)三种,如图13所示。 表面应力解除法在应力测量发展早期起到了很大的作用,但是这种方法也有很大的局限性,包括① 测量环境对应变计或者测量柱影响较大,例如湿度、灰尘和地下温度等;② 与扁千斤顶法类似,平面应力解除仅能测量地下洞室围岩表面的地应力,而围岩表面的应力容易受到洞室开挖工艺、围岩二次应力场、洞室表面应力集中等因素的影响,同时围岩表面的结构面和岩体的各向异性对测试结果影响较大,而且不容易消除;③ 这种方法测出的只是岩石表面的两个主应力,属于平面应力测量。 表2 原地应力测试和估算方法对比Table 2 Comparisons of in-situ stress estimate methods 图14 区域地应力场确定(估算)技术路线图(据Zang and Stephasson, 2010,有修改)Fig. 14 Technical flow chart to determine (estimate) a regional stress regime (According to Zang and Stephasson, 2010, modified) 地下空间开挖后,周边围岩必然会变形,而且这种变形非常明显,只要仔细观测地下空间围岩的变形过程,并求得地下空间围岩的岩体弹性模量或者变形模量,就可以估算工程区的原地应力场状态,通常人们称这种方法为反分析法。Zajic和Bohac(1986)、Sakurai和Shimizu(1986)首先提出了这种地下空间反分析方法。首先在地下空间一个或者多个断面上监测位移,并利用数值分析方法(有限元或者边界元)将其与区域应力场联系起来,这一过程需要假设岩体属性参数以及这些参数随深度的变化规律。Zou和Kaiser(1990)还提出了针对二维问题的反分析方法,后来Wiles和Kaiser(1994)将这一方法拓展到了三维,这种方法中是首先在岩体中预埋设应变仪、伸缩仪、闭合仪、倾斜仪等位移或者应变观测装置,然后观测后续开挖进行时这些仪器的记录响应,进而利用数值分析法(三维有限元或者三维边界元)来分析区域应力场。Martin(2003)认为,在深部高地应力区开挖过程中,基于地下空间变形的反分析法得到的原地应力状态更为准确,但是通常科技人员低估该方法的价值。 以上内容对目前所使用的较为常见的应力测试方法进行了回顾总结,不同的方法有不同的适用范围,也有不同的误差范围,这些方法的优缺点和适用范围列于表2。这些方法又可以分为主动法和现象分析法,主动法就是工程技术人员通过主动扰动原位岩体,通过观察扰动后的岩体响应特征,例如应变或者变形、破坏,再结合岩石力学属性参数的研究分析反演区域应力场特征,这包括水压致裂法、原生裂隙水压致裂法、扁千斤顶法、表面解除法等,这类方法比较适用于基础设施建设、资源和能源开发等领域的使用。其余的方法可以称之为现象分析法,因为只有发生了这些现象,通过分析这些现象所蕴含的应力信息,确定区域应力场,这些现象分析法可以作为主动法的有效补充,帮助人们更为准确地确定区域应力场。 与此同时,这些方法得到的应力信息所反映的岩石体积量是有较为明显的差别的,在联合使用不同方法时应对这种体量差别所带来的误差予以关注。例如套芯应力解除法只能反应100~300cm3范围内的岩体应力信息,而地下空间反分析法则可以反应100~300m3范围内的岩体应力信息,而断层滑动反演和火山口排列调查反应的岩体应力信息可能达到100~300km3。相对而言,建立在大体量岩体分析上的方法得到的应力数据对于研究区域构造应力场更为稳定可靠,但是不同的方法能揭示不同尺度上的应力信息,应根据需求适当调整所采用的应力测试或者估算方法。 通过对前面的应力测试或者估算方法的回顾和总结,我们也基本勾画出了开展一个地区地应力场分析的一般路径,如图14所示,可以包括四个主要步骤: ① 初步应力方向和量值估计,这一步中主要对现有资料进行了系统的分析总结,找出现有资料中的相互统一或者相互冲突的地方;同时可以利用地质学方法和地球物理方法对研究区应力场进行初步研究;如果有岩芯和钻孔,那么我们就可以利用岩芯和钻孔孔壁出现的现象开展部分初步应力分析;② 实地测量,这一步主要在第一步的基础上并结合现有的工程实践条件(如钻孔、定向岩芯和地下空间岩体),开展相应的应力测量分析;③ 基于两项工作的综合分析,进而对整个工作区的应力场状态进行预测分析,通常使用数值模拟手段;④ 对影响应力场分析的主要因素进行重点分析讨论,包括岩体结构、区域地质构造等因素,并给出参考结论。 Fairhurst(2003)曾对岩石(岩体)应力测量进行过详细的总结评述,他认为近些年来,岩体应力测量的理论基本没有大的发展变化,Zang和Stephasson(2010)也表达了类似的观点。近几年的岩石应力测量技术的发展集中体现在测试测备的革新进步方面,例如新一代Borre应变仪、水压致裂法四元封隔器(Zang and Stephasson, 2010)、BABHY测试设备等(Ito, 2010)。未来应力测量技术的发展仍然有可能集中体现在测试设备的革新进步方面,同时人类社会对能源和材料新的需求,对开展深部测量有了更高的要求,需要工程师和科学家们研发更多用于深部地壳应力测量的技术和设备;与此同时,随着计算机计算能力和岩石测试能力的不断提升,未来将会对有关岩石各向异性、非均质、非线性的属性特征对岩石或岩体中应力分布的影响有更深入的研究。
1.7 岩芯二次应力解除法
1.8 微裂隙岩相分析法
1.9 轴向点荷载分析法
2 基于钻孔的方法
2.1 水压致裂法
2.2 套筒压裂法
2.3 原生裂隙水压致裂法
2.4 套芯解除法

2.5 钻孔崩落

2.6 孔壁诱发张裂缝
2.7 钻孔变形
2.8 钻孔渗漏实验
3 地质学方法
3.1 地倾斜调查
3.2 断层滑动反演
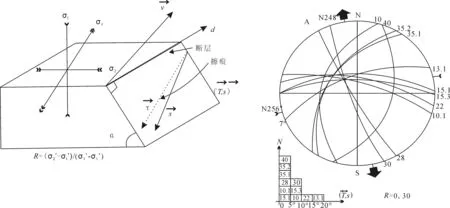
3.3 新构造运动节理测绘
3.4 火山口排列调查

4 地球物理学方法
4.1 震源机制解
4.2 其它地球物理测井方法
5 基于地下空间的方法
5.1 扁千斤顶法

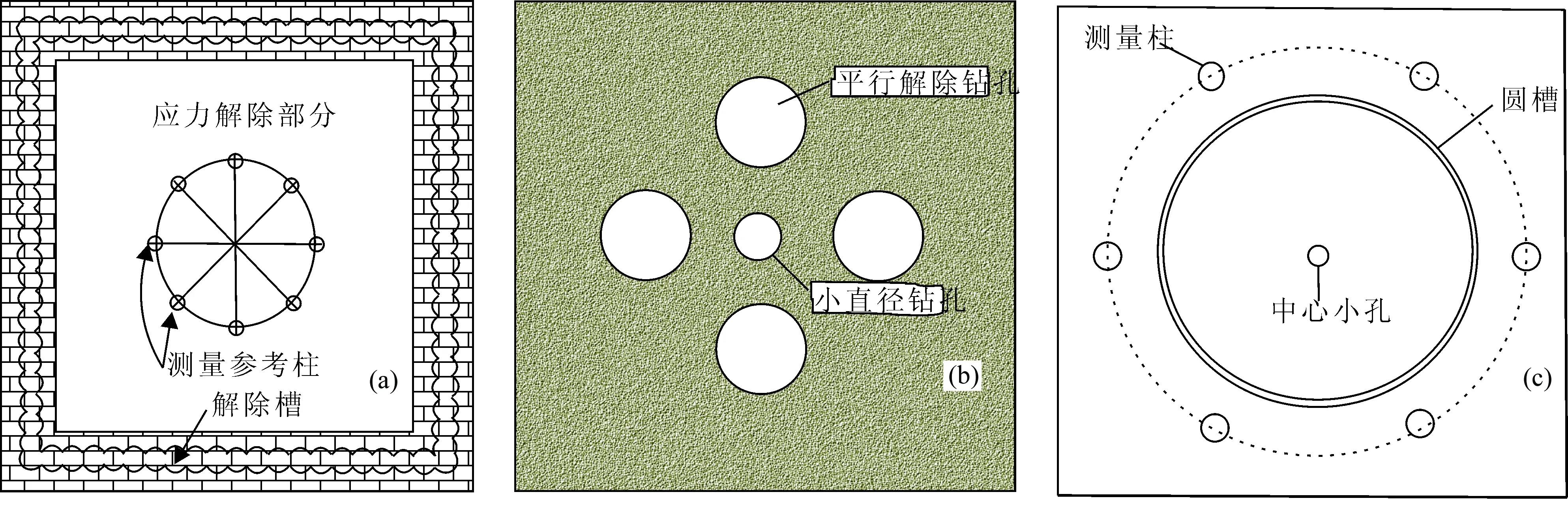
5.2 表面应力解除法

5.3 反分析法

6 讨论及展望
6.1 讨论
6.2 展望

