小妖助人类逼近绝对零度

吕之品

好好回忆一下，你最近一次跟妖精是在哪儿会面的？在小说中？在电影里？在漫画书上？……俱往矣！今天让我们到一个谁也意料不到的地方去见识一位妖精。不要笑，严肃点！虽然世界上妖精有千千万，但用途却有霄壤之别，有的供人发笑，有的却是供人思考的。你要想去见今天的这位妖精，需带上一颗勤于思考的脑袋。

你要去的地方叫“物理学”，妖精的名字叫“麦克斯韦小妖”。这位妖精很奇怪，它离开山林湖泽、岩崖洞穴，偏偏出现在从来不盛产妖精的物理学地盘上，还有一个拗口的外国人姓氏。实不相瞒，这个妖精是一位叫麦克斯韦的大物理学家为了解决物理问题而幻想出来的。

谈一点历史背景

19世纪，随着三大定律的提出，热力学这门学科已日趋完善。热力学第一定律实质上是能量守恒定律，在此不用赘述。我们今天要谈的是热力学第二定律，因为小妖就出在这儿。

只要你细心观察，就不难发现，生活中有许多过程是不可逆的。举个例子，一瓶敞口的香水放在房间里，香水不停挥发，香水分子充满整个房间，你不可能指望香水挥发完之后，某一天房间里所有的香水分子又自动钻回瓶子，重新出现一瓶香水……用物理学上的话说，香水挥发这个过程是不可逆的。

为了描述此类现象，物理学上引进一个“混乱度”的概念，并总结出一条定律：一个孤立系统总是朝着混乱度增加的方向演化。这就是热力学第二定律。这条定律是这么来解释香水挥发为什么不可逆的：香水分子充满整个房间之后，比起当初装在瓶子里时，更显得无序，混乱度变大了，因为原先的它们仅局限在瓶子里跑，而现在却可以满屋子乱跑。当然，混乱度并不是一个模糊的概念，事实上它是可以严格计算的。

虽然热力学第二定律跟日常经验相符，但物理学家还是觉得它怪怪的。为什么呢？以香水挥发为例：对于每个香水分子来说，它既可以自由地离开瓶子，也可以自由地返回瓶子，根本就不存在“不可逆”一说。我们还可进一步说，最终支配每个香水分子运动的是牛顿三大定律，而牛顿定律是完全可逆的。

既然如此，那热力学所谓的“不可逆”又从何而来？统计物理学家巧妙地回答了这个问题。还是以香水挥发为例，统计物理学家说，要重新出现一瓶香水，就必须让房间里分散在各个角落的数以亿计的香水分子在某个时间一起回到瓶中。但可以试想这有多难，比如第一个分子回到瓶中之后，它必须老老实实呆在瓶中，等第二个分子飞进来，然后这两个分子在瓶中又等第三个分子飞进……等等，依次类推；而事实上，这中间更多的是发生“按下葫芦起了瓢”的情况，比如说没等第二个分子飞进瓶子，第一个分子已经又飞出瓶子了，数以亿计的分子几乎没有重新聚首的机会。

所以，热力学上所谓的不可逆，不是说不允许发生，按统计物理学家的观点，只是发生的可能性非常小，几乎等于不会发生而已。

其实此类事情我们自己也有体会，比如一个外省的班级毕业了，大家各奔东西。虽然班里所有人一生中都有几次上北京的机会，但除非事先约好，否则所有人某一天完全出于偶然在北京相遇的机会几乎是不存在的。

小妖出场与物理学家对第二定律的挽救

如此看来，热力学第二定律只是一个统计学规律，只有当涉及大量分子时才严格成立，并不适用于单个分子或者分子数很少的系统，因为分子数越少，可逆程度越高。这就是它的局限性。

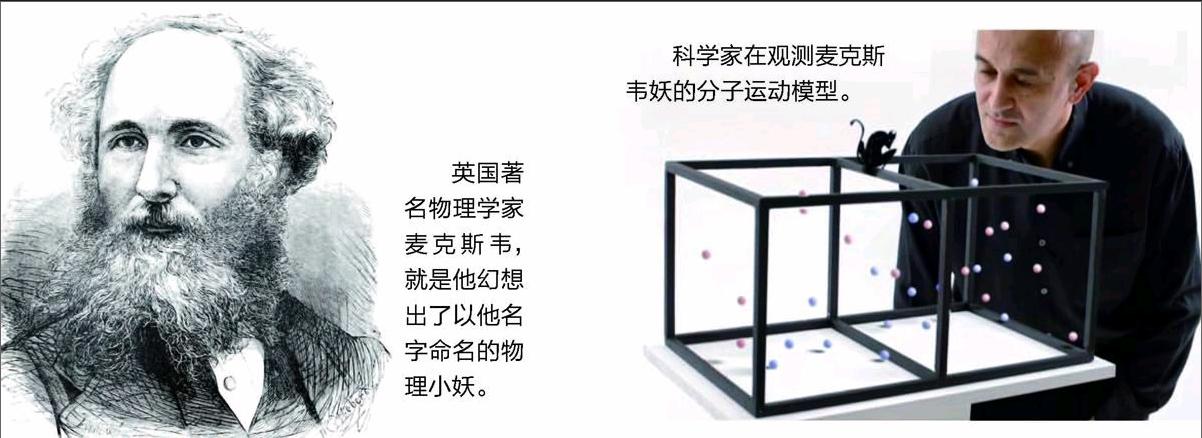
为了让大家进一步认清这条定律的局限性，19世纪英国伟大的物理学家麦克斯韦设计了这样一个思想实验。

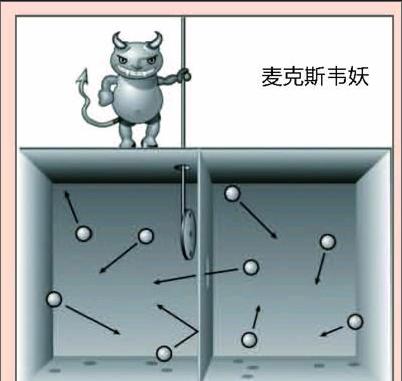
假设在一个密闭容器里充满了温度均匀的空气，虽然温度均匀，但统计物理学却告诉我们，其实里面所有分子的运动也并非整齐划一，依然存在着速度较快和较慢的分子，为了方便起见，我们不妨把前者称为热分子，后者称为冷分子。

现在把容器分为A和B两部分，在分界处开个小孔，由一名小妖守着。这名小妖可以迅速判断哪个是热分子，哪个是冷分子，并且身手矫捷，能迅速地打开或关闭小孔。它的操作规则是：对于从A来的分子，是热分子，就打开小孔，让它跑到B，冷分子则不放行；对于从B来的分子，让冷分子跑到A，热分子则不放行。为了开启或关闭时都不消耗能量，我们还可以把小孔的门枢纽做得无限光滑。久而久之，A里面热分子越来越少，温度越来越低，B里面热分子越来越多，温度越来越高。热力学第二定律原先说，冷热气体混和之后的混乱度比混和之前的大，所以混和过程是不可逆的，但现在事实上冷热气体又被小妖重新分开了，而且这中间没有消耗额外的能量。

前面说热力学第二定律不适用于分子数很少的系统，而现在麦克斯韦通过这个思想实验告诉我们：即便系统里分子数很多，只要在里面“安插”这样一个小妖，热力学第二定律也依然可以被破坏。因为现实中虽然小妖不一定存在，但理论上却没有一条科学定律禁止它存在。

如此一来，热力学第二定律就岌岌可危了。不过所幸，1920年代，匈牙利物理学家西拉德指出，在这个思想实验中热力学第二定律并没有被推翻。

西拉德的分析是这样：在这个实验中我们应该把容器里的气体和小妖当作一个系统考虑。在小妖的操作中，有两个步骤对整个系统造成影响。第一是小妖通过小孔的门，使冷热气体分子分开，这一操作使系统的混乱度减少。但为了做到这一点，它不得不涉及第二个步骤，即必须事先取得有关分子位置和速度等信息。怎样取得这些信息呢？简单的办法是它向每个分子发射一束电磁波，然后分析反射波。在这个过程中，发射出去的电磁波原来波长和传播方向都是比较整齐划一的，但被分子朝四面八方散射之后，就变得混乱了，所以这一步骤增加了系统的混乱度。把这两个过程合并考虑，总体来说系统的混乱度还是增加了。

小妖现身，帮助冷却

上面的讨论看起来都是玄而又玄的东西，谁都不会认为麦克斯韦小妖真实存在，西拉德的分析也只停留在理论推测上，这个问题看来似乎永远要悬而不决，但没想到最近物理学家真的实现了麦克斯韦的这项思想实验。更有甚者，他们还驾驭小妖，向绝对零度逼近。

让我们先来看麦克斯韦小妖何以能够冷却气体。假设有一个充满气体的容器，内壁没有摩擦。现在用固定隔板把它分成A、B两部分，隔板上开个小孔，由小妖把守。小孔的门是单向的，比如说小妖只让A的分子跑到B去，反过来则不行。久而久之，A中的气体分子将全部跑往B，A成了真空。最后，隔板在B中气体压强的作用下，向A移动，直到占满整个容器。这个过程中，气体对隔板做功，隔板获得额外的动能（在没有摩擦的情况下，隔板运动会越来越快），所以气体的温度就下降了。

注意，上述气体在容器B部分聚集的过程与我们平常把A里的气体压入B可不一样。如果气体是压进去的，那么由于外界对气体做了功，气体的温度不降反升，而在小妖的帮助下实现的“压缩”则在“压缩”的同时可以保持温度不变。

现在让我们来看物理学家如何利用麦克斯韦小妖来冷却原子。为了避免容器壁把热量传给有待冷却的原子，我们不把原子装在有形的容器里，而是通过磁场把它们约束在某个空间，磁场就像一个无形的“容器”，阻止它们扩散出去。

假设这些原子有两种稳定的能量状态（原子核外电子所处的轨道决定原子的状态），为方便起见，我们在图中把能量低的状态标为蓝色，能量高的状态标为红色。在一定频率激光的照射下，原子可从蓝色状态变成红色状态。激光的能量全部转化成了原子内部的能量（也就是说，原子的静止质量增加了），就好比人储存了脂肪一样，不会增加原子的动能，所以照射后原子的温度保持不变。

现在打开一束激光（橙色），将“容器”隔为两半。这束激光只对红色原子起作用。对它们来说，它就像是一堵无形的墙，一碰上就反弹回去。

打开第二束激光（红色），这束激光只照射右侧，如果击中原子，就会把原子从蓝色变成红色状态。

红色原子被橙色激光反弹，所以只能呆在“容器”右侧。

左边蓝色原子不断往右边跑，右边的蓝色原子不断转化成红色原子，而这些红色原子又被橙色激光限制在了右边，久而久之，原子都集中到了右边，左边变成了真空。

关闭两束激光，让这些原子慢慢扩散回初始的体积，于是温度就降低了。物理学家在这个实验中，把原子的温度降到了0.000015K。

你也许会问，那位大名鼎鼎的小妖又在哪里呢？说出来也许很让你失望，在这里橙色激光就扮演了麦克斯韦小妖的角色。真是不可貌相啊，虽然它没长尾巴，没有妖气，以致让人辨认不出来，但它确确实实实现了麦克斯韦当初赋予小妖的全部本领。你看，它对红色原子就起到了单向门的作用，不允许右边的红色原子跑到左边去——当然了，由于在这个例子中，左边一开始就没有红色原子，这个单向门实际上只起到一堵墙的作用。

激光是单向性非常好的光，本来很有序，但当橙色激光作用在红色原子上，被反射之后，就变得非常无序，这过程增加了系统的混乱度。而把全部原子“压缩”到“容器”右边则是一个混乱度减少的过程。科学家通过计算表明，增加的量比减少的量多，所以系统总体上混乱度增加了。系统并没有违反热力学第二定律——这正是西拉德当年所预言的。

在很多故事中，妖精带着捣鬼、促狭的意图而来，最后往往被我们收服，替人类做好事。看来，麦克斯韦小妖也没逃出这个祖传老例。