城市轨道交通列车开行方案优化模型研究

杨 东，江雨星，宋 岩

（兰州交通大学 交通运输学院，甘肃 兰州730070）

城市轨道列车开行方案的优化设计问题可看作是一个双层决策问题，其中的上层决策部门是地铁运营企业，下层决策者是乘客。上层规划描述地铁运营企业制定最佳的列车开行方案以满足本企业的目标，下层规划则描述了地铁客流在不同出行方案间的分配模式，分配的原则是每个乘客都选择使自己广义出行费用（满意度）最低的出行方案。双层规划可以同时分析决策过程中两个不同的、相互矛盾的目标，事实上的平衡点也就是双层规划问题的最优解。因此，本文主要采用双层规划来研究城市轨道交通列车开行方案的优化问题。

1 模型的建立

1.1 假设条件设置

本文在建立城市轨道交通列车开行方案模型前做如下假设:

1.1.1 车站、线路的分布

对于1条城市轨道交通线路，有n个车站，双线，列车从车辆段出发的方向为上行方向，反之，为下行方向。

1.1.2 列车运行特性

轨道列车采用混合交路（又称为长短交路），长短交路列车在线路的部分区段共线运行，长交路列车到达线路终点站后折返、短交路列车在指定的中间站单向折返。

1.1.3 乘客排队等待现象

在建模时应充分考虑排队等待现象对列车开行方案的影响。为简化模型，假定无退票乘客，即所有购票乘客都等待乘车，没有流失情况。

1.1.4 列车停站方案

只考虑站站停的情况，不考虑区段停站、跨站停车和快慢车方案。

1.1.5 乘客对车次的选择

只选择能够直达目的站的车次，不考虑中间换乘情况。

1.2 参数设置与符号说明

参数设置及符号说明如表1所示。

表1 参数设置及符号说明表

1.3 决策变量分析

本文研究的城市轨道交通列车开行方案决策的主要问题包括:列车编组数量，列车开行对数，列车发车时刻，列车交路方式，乘客数量统计，乘客车次选择，乘客等待时间。相应的变量设置如下:

1）zk为k次列车编组量数，k∈K；

2）tjk为k次列车在j站发车时刻，j∈J，k∈K；

4）Pjk为k次列车在j站发车时刻列车上的乘客数，j∈J，k∈K；

6）ωi为乘客i的等待时间。

1.4 目标函数研究

1.4.1 地铁运营部门成本函数（上层模型）

地铁运营部门的成本主要由两个因素决定，即列车运营成本和其他固定成本。

1.4.1.1 列车运营成本

列车运营成本包括两部分:列车的每列车公里费用CT和列车的每辆车公里费用Cu。CT与每个列车开行时段列车开行对数dt和列车运行区段的里程L（j1，j2）有关。Cu与每列车的编组长度zk，每个列车开行时段的列车开行对数dt和列车运行区段的里程L（j1，j2）有关。考虑到列车的交路方式，则列车运营成本为

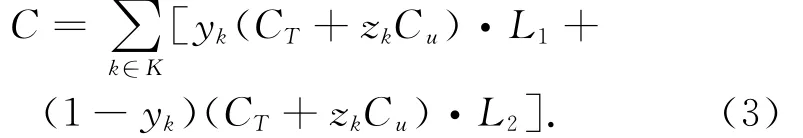
1.4.1.2 其他固定成本

地铁部门的固定成本包括工作人员工资、设备日常损耗等固定成本，用Q表示。

1.4.1.3 地铁运营的总成本函数

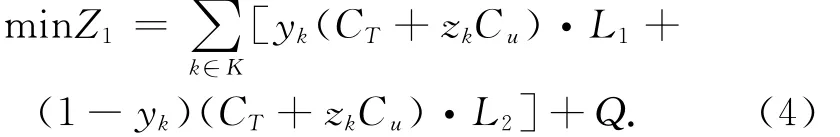
1.4.2 乘客满意度函数（下层模型）

1.4.2.1 旅行时间

乘客的旅行时间包括候车时间和乘车时间。由于列车运行时间已知而且不考虑换乘，因此，本文只考虑乘客的候车时间，其公式为

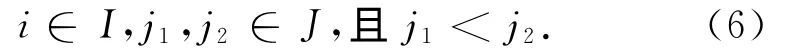
1.4.2.2 舒适度

本文考虑的旅客舒适度是指乘车的舒适度，用列车开行对数来衡量，增加开行对数，可以减少列车的拥挤程度，提高旅客的舒适度，并且可以缩短旅客的乘车等待时间，使旅客更容易、更方便乘车，因此，舒适度用dt衡量。

1.4.2.3 旅客满意度函数

α1，α2分别为列车开行方案的候车时间和列车开行对数对旅客满意度的权重系数，且α1＋α2＝1，由于候车时间对旅客满意度起负作用，因此，其权重系数取负值

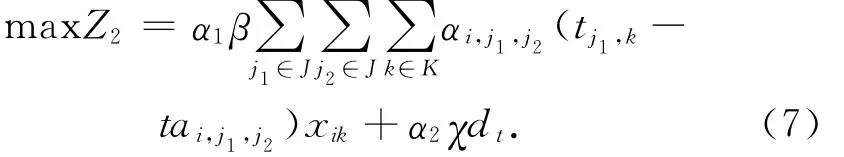
1.5 约束条件分析

1.5.1 上层规划约束条件

1.5.1.1 列车追踪间隔及出发时刻

对于城市轨道交通，必须保证前后2列列车在起点站的发车间隔时间满足安全追踪要求。考虑到开行方案的制定是在一个调度时段内，则有

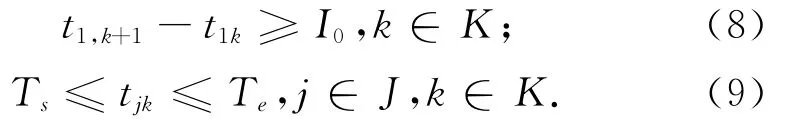
1.5.1.2 列车上乘客数量统计

轨道列车到达车站后，部分在车乘客将在该站下车，而在车站等待的乘客则按照一定的规则上车，当车上人数达到载客能力时，未上车的乘客将等待下一趟列车，由此可以得到

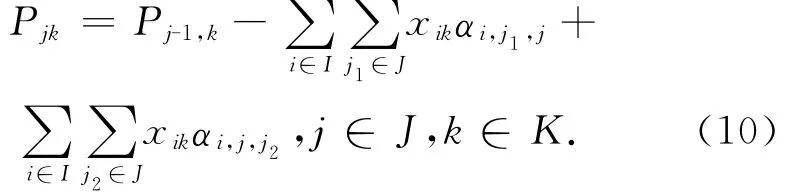
考虑到列车定员限制，乘客人数应不大于最大载客人数。则有

1.5.1.3 通过能力约束

通过能力可用下式表示

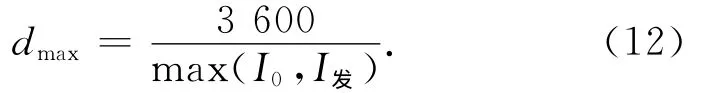
所以，每个列车开行时段的列车开行对数都不能超过线路所允许的最大通过能力，即

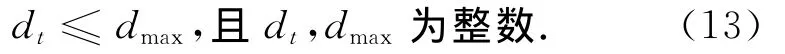
1.5.2 下层规划约束条件

1.5.2.1 乘客选择乘坐列车车次

乘客i只能选择乘坐一趟车，则有

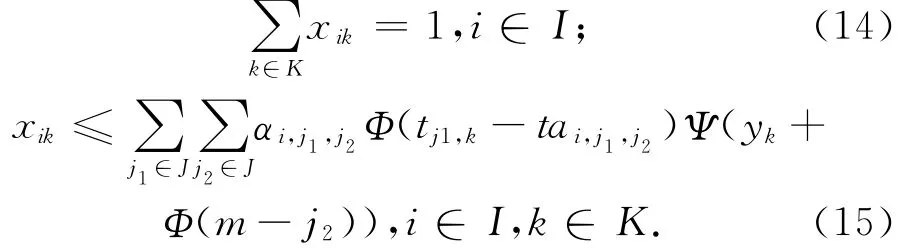
其中

乘客i在j1站候车，目的站为j2站（即αi，j1，j2＝1），当k次车在j1站的出发时刻tj1，k≥乘客i在j1站到达时刻tai，j1，j2（即Φ（tj1，k－tai，j1，j2）＝1）时，乘客才有可能乘坐k次车。此外，考虑到列车长短交路问题，只要列车为长交路（即yk＝1），则不管乘客到站j2是否大于短交路列车途经车站数目，乘客都可以选择乘坐，若列车为短交路（即yk＝0），当且仅当乘客到站j2不大于短交路列车途经车站数目m时，乘客可以选择乘坐，否则乘客不选择乘坐，等待下一趟车。最后，若是满足上述约束条件，但由于乘客数量太多，不能全部上车，则须等待下一趟车。

1.5.2.2 乘客i的候车时间

乘客i在j1站乘上k次车的等待时间应为k次车在j1站的出发时刻减去乘客i到达j1站的时刻

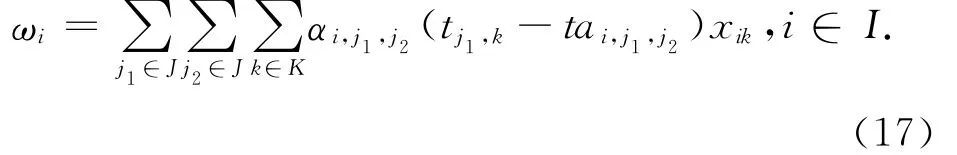
1.5.2.3 其他约束条件

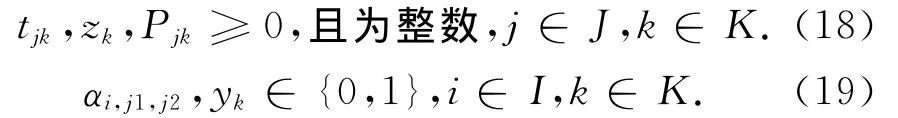
1.6 综合模型

综合前几节分析，得到城市轨道交通列车开行方案的综合双层规划模型为

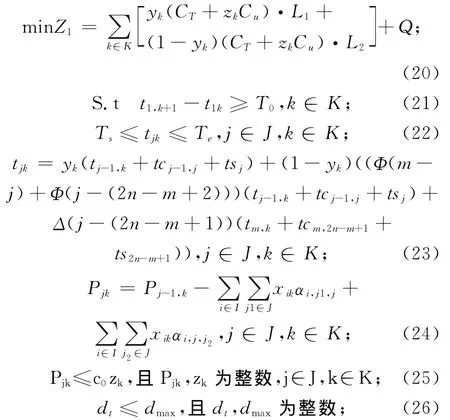
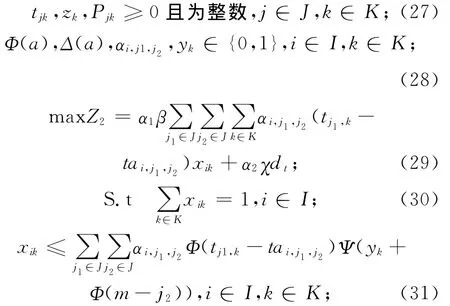
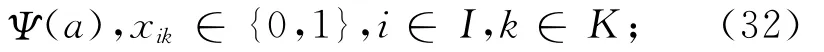
2 实例分析

2.1 线路概况与数据统计

本文以深圳市地铁3号线作为研究对象，利用这条线路的预测客流数据以及各项技术指标参数，具体实施各项优化步骤。

2.1.1 基础数据

1）站间距及区间运行时间，如表2所示。

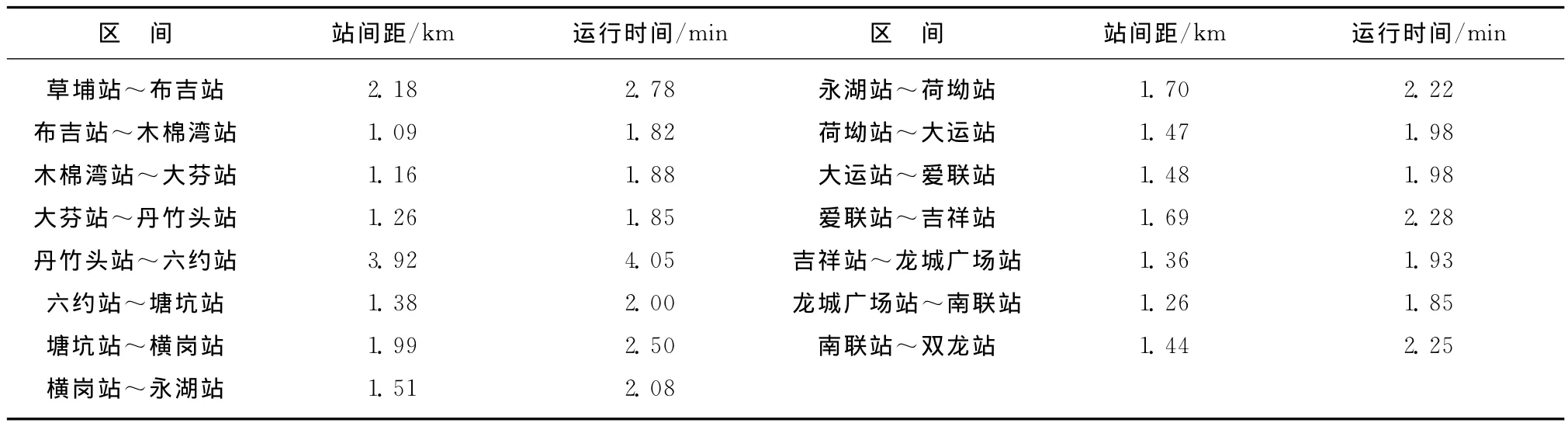
表2 站间距及区间运行时间

2）停站时间如表3所示。

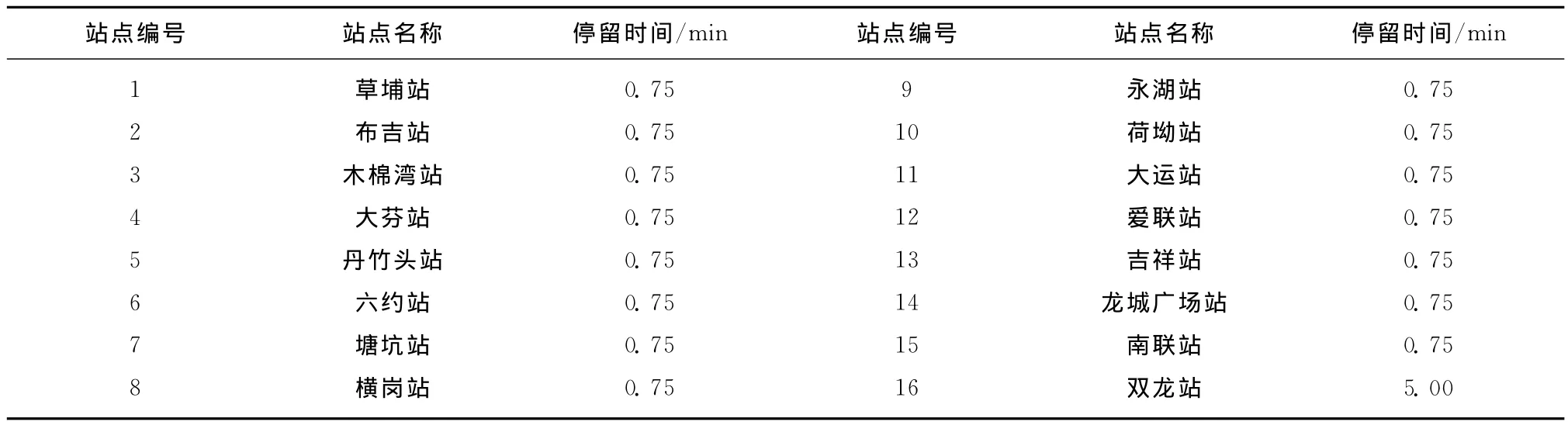
表3 停站时间

2.1.2 其他数据

其他数据如表4所示。

表4 其他数据参数及取值

2.2 计算结果分析

将所给数据代入模型，乘客到达车站的时刻和乘车区间人为给定，使用LINGO计算得到最优解。

2.2.1 列车相关信息统计（对应上层规划）

对应上层规划的列车相关信息统计，如表5所示。

表5 列车相关信息统计

2.2.2 乘客相关信息统计（对应下层规划）

对应下层规划的乘客相关信息统计，如表6所示。

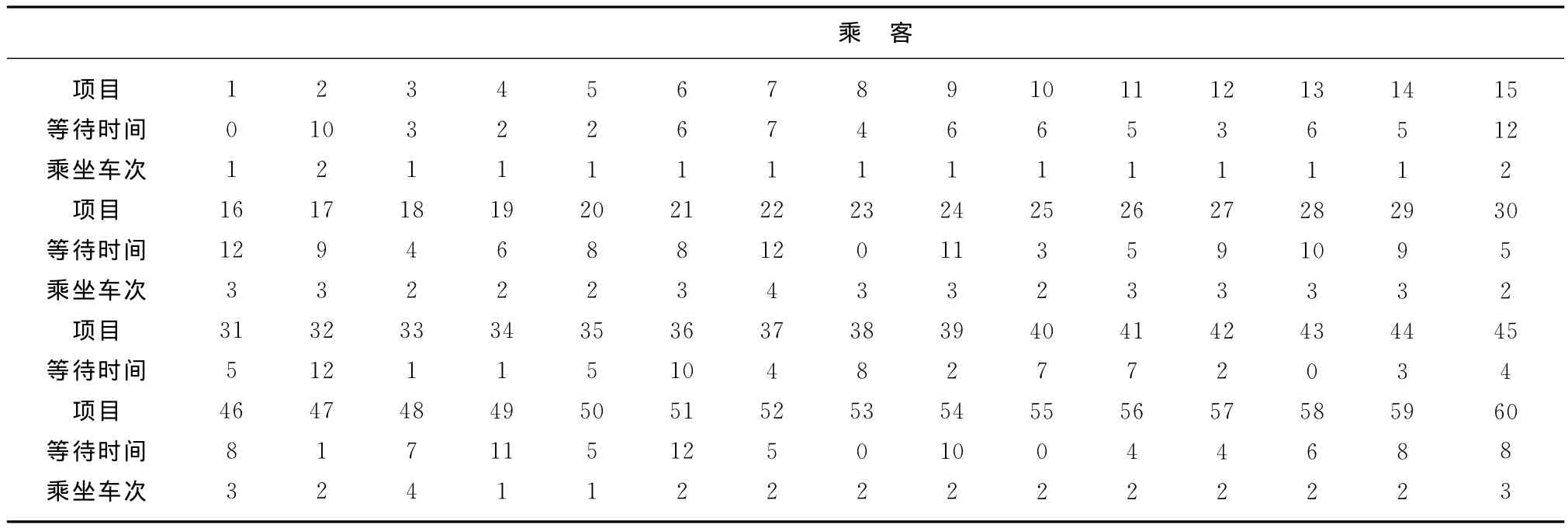
表6 乘客相关信息统计

综上所述，所有决策变量都得到求解。使地铁部门和乘客都满意的函数目标值为4428.640元。研究时段共发4列车，每列编组6辆，列车发车时刻和发车间隔与客流需求的变化规律基本吻合，采用非等间隔发车的均衡开行模式。该模式能在一定程度上缓解排队等待和能力虚靡现象，乘客的平均等待时间为5.72min。

3 结 语

本文从城市轨道交通运营部门和乘客两个方面入手，做到地铁部门成本最小化、乘客满意度最大化是建立模型的最终目标，也是列车开行方案实施的优化目标。从不同方面对决策变量进行约束，最后得到城市轨道交通列车开行方案的双层规划优化模型。以深圳市地铁3号线作为研究对象，利用LINGO对模型编程求解，验证了模型及算法的可行性和有效性。本文以客流量预测为基础建立了城市轨道交通列车开行方案的优化模型，体现了开行方案和客流量间的相互影响关系。

［1］牛惠民，陈明明，张明辉.城市轨道交通列车开行方案的优 化 理 论 及 方 法 ［J］.中 国 铁 道 科 学，2011，32（4）:128－133.

［2］姜毅，王卫.城市轨道交通沿线常规公交线网评价分析［J］.交通科技与经济，2013，15（4）:97－99.

［3］张明辉.基于GP算法的城市轨道交通客流分配问题研究［J］.交通科技与经济，2014，16（3）:46－49.

［4］严波.城市轨道交通运营组织优化研究［D］.南京:东南大学，2006.

［5］孙运奇，展晓义.南京地铁一号线大小交路运行方式分析［J］.交通世界，2008，7（14）:122－123.

［6］曾海军.南京地铁一号线列车运行模式分析［J］.兰州交通大学学报，2007，26（6）:80－83.

［7］刘浩江.地铁运营中的行车调度调整策略［J］.都市快轨交通，2006，19（6）:1－3.

［8］曹阳.城市轨道交通实时调度方法研究［D］.吉林:吉林大学，2009.

［9］杨同庆.基于弹性需求的客运专线开行方案优化设计研究［D］.北京:北京交通大学，2009.

［10］陈胜波，何世伟，何必胜.客流波动条件下城市轨道交通列车开行方案研究［J］.城市轨道交通研究，2013，10（10）:53－58.

［11］邓连波，增强，高伟，等.城市轨道交通列车开行方案优化方法［J］.中国科技论文在线，2010，5（10）:767－772.