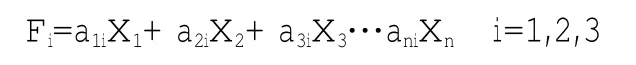因子分析法在地区综合评价中的应用——以湖北省为例

●武汉大学经济与管理学院 赵 昕

因子分析法在地区综合评价中的应用
——以湖北省为例

●武汉大学经济与管理学院 赵 昕

近年，对湖北省在中部地区综合竞争力的评估主要集中在经济方面，对于人文、环境、社会等多方面的综合考量则较少。因子分析法可有效综合各方面的评价因素，基于各因素所包含的信息量进行整合，更具有效性。本文用因子分析方法对中部六省份进行综合排序，结果表明，湖北省在2012年表现最好，各项因子排名居第一，工业增速显著，人口自然增长率控制较好，但是物价水平涨幅较快，需进一步改善。其他几省综合排序为安徽、湖南、江西、山西、河南。

综合竞争力评价 因子分析 应用

一、引言

“十二五”时期，我国发展处于可以大有作为的重要战略机遇期，经济社会发展长期向好的基本态势不会改变。湖北省地处长江中游，坐拥九省通衢，作为我国交通和通讯的枢纽，华中地区的工商业和金融中心，应抓住机遇，加快发展。世界经济格局深度调整，投资和贸易保护主义进一步抬头，发展的外部环境更趋复杂；沿海发达地区结构调整和产业升级步伐明显加快，在新一轮经济增长中占据有利地位；周边省市经济发展势头强劲。湖北省面临前所未有的竞争压力，必须增强忧患意识。

关于中部崛起的分析，主要集中在政策、制度、发展路径、影响因素等方面，除此之外还有在中部崛起的大环境下，探讨湖北省的发展策略以及对中部崛起和武汉城市圈的关系研究。昝国江、安树伟（2011）指出了中部区域经济发展的总体思路及重点领域如大力推进城市化进程，并在此基础上提出了相应的政策建议1。武清华等（2011）针对当前经济状况提出了中部6大城市群的发展策略2。张湖林（2011）以武汉城市圈为例，分析了武汉城市圈对中部崛起的带动作用3。苏娜（2008）指出湖北要成为促进中部崛起的重要战略支点所面临的问题与策略4。

那么，湖北省目前的发展状况如何，怎样在“十二五”背景下，抓住机遇，实现快速发展等都是我们面临的问题。本文借助因子分析对中部六省综合情况进行排序，而不是单纯的对某一项指标的排序，更具综合性，评价更为全面、可靠。

二、因子分析法简介

因子分析的基本思想是通过对变量的相关系数矩阵内部结构的研究，找出能控制所有变量的少数几个随机变量去描述多个变量之间的相关关系，但在这里，这少数几个随机变量是不可观测的，通常称为因子。然后根据相关性的大小把变量分组，使得同组内的变量相关性较高，但不同组的变量相关性较低。

(一)因子分析的数学模型。可观测随机变量X=(X1，X2,X3……Xp)'标准化后得到Y=(Y1，Y2,Y3……Yp)'，其均值E(Y)= 0，协方差矩阵D(Y)=∑。

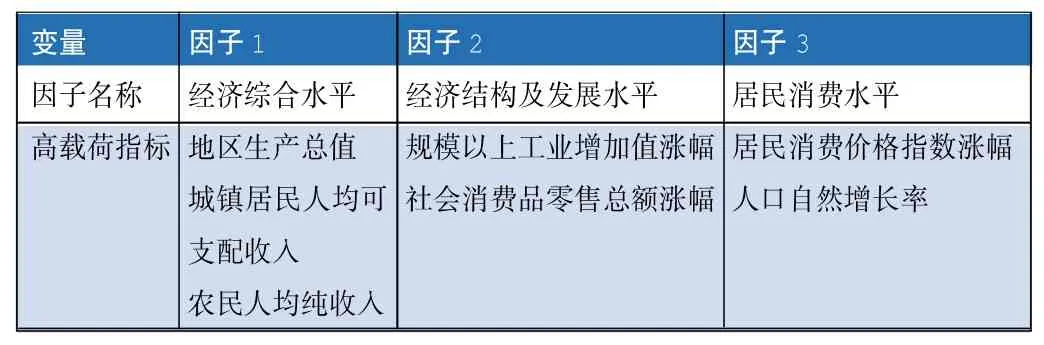
设 F=(F1，F2,F3……Fm)'（m

随机向量Y可以表示为正交因子模型（1）：简记为：Y=AF+ε。

(二)因子分析步骤。将原始数据基于原始数据的均值和标准差进行z-score标准化，即，式中Xi和Si分别为指标Xi的样本均值和标准差。

用主成分分析法进行因子分析，得到相关系数矩阵的特征值及特征向量，根据因子贡献率选取公共因子。在对公共因子矩阵进行最大方差正交旋转后，得到旋转后的因子矩阵，还将获得累计贡献率、共同度等数据。

计算各样本的综合因子得分，并对其进行排序，统计各类样本中综合得分大于平均水平，即平均值为0的个数，从而得到各类样本的排名。

三、湖北综合竞争力的因子分析

(一)样本及变量指标的选取。本文选取了2012年，中部六大省份的11项经济指标，包括地区生产总值、规模以上增加值涨幅、外贸出口总额等。

表1 相关系数矩阵的特征值与贡献率

(二)因子分析的结果。下文将解释因子分析的结果：

1.求相关系数矩阵的特征值与贡献率。通过SPSS17.0软件计算，得到经标准化处理后的各项财务指标的相关系数矩阵的特征值与贡献率，如表1所示。从表中可以看出，变量的相关系数矩阵有3个数值大于1的特征值。累计贡献率为87.286%，即它们一起解释了中部六省份经济水平标准差的78.572%。

2.建立因子载荷矩阵。对三个因子F1、F2、F3进行方差最大正交旋转后，得到因子载荷矩阵。如表2所示：同时,将指标值载荷矩阵中载荷较高的情况分为三类。可以依此给各个公共因子命名，如表3所示：

表2 旋转后的因子载荷矩阵

表3 各因子名称及高载荷指标

表中第一个因子在地区生产总值、城镇居民人均可支配收入、农民人均纯收入有较大的载荷。而这些指标能够反映地区的总体情况以及人民生活水平，故称其为经济综合水平。第二个因子在规模以上工业增加值涨幅、社会消费品零售总额涨幅上有较大的载荷，而二者是对地区经济不同侧面的反应，故将其命名为经济结构与发展水平。第三个因子在居民消费价格涨幅、人口自然增长率上有较大的载荷，二者反映一个地区的居民消费水平。表4为因子得分系数矩阵,可用于计算各因子的值。公式为：

表4 因子得分系数矩阵

(三)结果分析。基于每个因子只能反映地区经济的某项能力，故以各因子特征值的贡献率为权重加权来计算各省份的综合因子得分，公式如下：

F=(47.509F1+25.029F2+14.748F3)/87.286

表5 给出了各省份的综合因子得分：

从表5中可以看出，湖北省不仅在各个因子上排名第一，而且在综合排名上也是位列第一。说明湖北省在2012年，经济发展较快，相比于消费而言，工业增速显著，人口自然增长率控制较好，但物价水平需进一步加强调控。

本文通过对湖北省综合水平进行实证分析，定性与定量相结合地分析了湖北省省内、省外经济环境存在的问题，提出了相应的解决方案。 “十二五”期间的湖北省经济正处于高速发展阶段，较好地处理内外部问题，对今后的发展至关重要。■

1.昝国江、安树伟.2011.“十二五”时期中部崛起政策调整研究我国中部崛起的城市群发展策略思考 [J].经济体制改革，5。

2.武清华、姚士谋、薛凤旋、张落成.2011.我国中部崛起的城市群发展策略思考[J].长江流域资源与环境，4。

3.张湖林.2011.论促进中部崛起的城市带动战略——以武汉城市圈为例[J].中南民族大学学报（人文社会科学版），1。

4.苏娜.2008.中部崛起背景下提升湖北核心竞争力研究[J].湖北社会科学，3。