地球自转及天体作用力对精密离心机的影响

凌明祥，王珏，宁菲，卢永刚，李明海，黎启胜

（中国工程物理研究院总体工程研究所，四川 绵阳 621900）

精密离心机是标定、校准加速度计等惯性仪表在高过载条件下输出性能及参数的测试设备，其产生的加速度准确度直接影响被测惯性仪表的检定精度［1］。因此，提高精密离心机输出加速度的准确度对惯导系统具有重要的理论意义及实用价值。

对于加速度相对标准不确定度为10-6量级的高精度精密离心机，在建立加速度载荷模型时除了考虑离心力、重力外，还需要分析由地球自转而作用在加速度计上的科里奥利力以及月球和太阳的作用力。此外，精密离心机中存在的各种失准角使得上述各力产生的加速度在加速度计输入轴上进行再分配，故输入到加速度计上的加速度是上述各种力与各种失准角综合作用的结果。文献［2－4］建立的精密离心机输出加速度载荷模型中含有科氏加速度，但没有分析失准角的影响。以往研制精密离心机的精度指标相对较低，大多数学者未考虑月球和太阳对精密离心机的影响。但对于精度为10-6量级的高精度精密离心机，月球和太阳作用力的影响是否能忽略需要仔细研究。文献［5］建立的精密离心机加速度载荷模型只考虑了地球和月球之间的万有引力。实际上，月球对精密离心机的作用力是地球的万有引力与地月之间的“惯性离心力”的合力［6］。笔者计算、分析了科里奥利力以及月球和太阳作用力对10-6量级精密离心机的影响，为相关精度的精密离心机研制提供参考。

1 地球自转对精密离心机的影响

1.1 失准角齐次变换矩阵建立

加速度相对标准不确定度为10-6量级的精密离心机机械系统主要由基座、空气轴承、转盘、定位平台以及加速度计夹具等组成。虽然是高精密加工与装配，实际上转盘径向与本地水平面之间存在一定夹角，称为转盘径向相对地面的俯仰失准角（图1中的λ1）。加速度计输入轴与转盘径向不平行，即出现加速度计的安装失准角，用加速度计输入轴相对转盘的俯仰失准角λ2及加速度计输入轴与转盘径向之间的方位失准角β来表示，如图1所示。

以转盘径向与加速度计质量中心线的交点为坐标原点，转盘径向为x轴（向外为正）建立转盘的空间坐标系o0-x0y0z0，其中z轴垂直于转盘表面指向天空为正。理想情况下，待标定加速度计的输入轴、摆轴和输出轴分别沿转盘径向x0轴、y0轴和z0轴。当存在安装失准角时，加速度计坐标系o1-x1y1z1可看作是在转盘坐标系o0-x0y0z0基础上，先绕y0轴旋转λ2角度，再绕z0轴旋转β角度后形成。采用齐次变换方法，加速度计坐标系相对于转盘坐标系的姿态矩阵为：

图1 俯仰失准角与方位失准角示意Fig.1 Misalignment angles

1.2 加速度计输入轴上科氏加速度计算

由于地球自转，处于地球表面随精密离心机一起旋转的加速度计要受到科里奥利力的影响，根据达朗贝尔原理，该力对加速度计产生的加速度（在此简称科氏加速度）为［7］：

式中：Fc为科里奥利力；m为加速度计质量；v为加速度计的线速度；ωε为地球自转角速度。

如图2所示，设以角速度ω按逆时针方向旋转的精密离心机位于北半球，其所在地的纬度为θ，转盘径向相对于地表的俯仰失准角为λ1。地球自转角速度ωε可分解为与转盘表面平行的分量ω1以及与转盘表面垂直的分量ω2。根据矢量叉乘定义，的方向垂直于转盘表面，的方向沿转盘为径向且指向外为正，大小为：

图2 精密离心机上地球角速度分解Fig.2 Rotational angular velocity of the earth decomposing on precise centrifuge

式中：α为加速度计线速度与地球自转角速度水平分量之间的夹角，α=ωt；R为精密离心机工作半径。

由于俯仰失准角λ2和方位失准角β的影响，科氏加速度将在加速度计输入轴上进行分配。由前文所建立的失准角齐次变换矩阵，加速度计三个轴上感知到的科氏加速度为：

忽略计算过程，当精密离心机沿逆时针方向旋转时，输入到加速度计输入轴上的科氏加速度为：

当精密离心机顺时针方向旋转时，式（6）中aI取负。该式适用于各种加速度不确定度指标的精密离心机，但式中待测分量有3个，不仅会增加测量系统的复杂程度，同时还会增大加速度不确定度评定值，需要对其进行简化。

1.3 科氏加速度量级分析及简化

四川地区纬度θ取30.7°，地球自转角速度取ωε=7.29×10-5r/s，sinα取最大为1。对加速度范围为（1～100）g的精密离心机，其角速度ω按a=R·ω2近似计算，得到ω的范围为：3.13～31.3 r/s，取ω=3.13 r/s进行计算。为了简化问题，λ1，λ2和β按相同的量值变化，记为λ，即：λ=λ1=λ2=β。

精密离心机的失准角一般不会超过100"。在该范围内，相对科氏加速度a′1（科氏加速度除以精密离心机输出加速度值）随失准角λ变化的曲线关系如图3所示，其量值在10-5数量级变化。因此，对于加速度相对标准不确定度为10-6量级的精密离心机，必须考虑科氏加速度的影响。

图3 相对科氏加速度随失准角的变化关系Fig.3 Coriolis acceleration curve with misalignment angle

若将式（6）的科氏加速度数学模型简化为aI=2ωωεRsinθ，经计算失准角λ1，λ2和β小于100"时，该简化运算产生的最大相对误差不超过2×10-8，该相对误差远远低于10-6。因此，按照失准角不会超过100"的假设，对于精度为10-6量级的精密离心机，加速度计输入轴上感知到的科氏加速度可简化为：

当精密离心机顺时针旋转时，式（7）取负。实际上，以上分析过程留有一定余量，即式（7）在一定程度上也适用于更大失准角以及更高加速度不确定度指标要求的精密离心机。

2 月球和太阳作用力的影响

绕转着的天体要受到相互之间的万有引力和由于绕转而产生的惯性离心力的作用［8］。就整个天体而言，万有引力与惯性离心力平衡，但对于地球表面的质点此二力并不平衡。相对地月系统，精密离心机可近似为质点，如图4所示。精密离心机受到月球的作用力为月球与精密离心机之间的万有引力与地月之间的惯性离心力的合力。

图4 月球对精密离心机的作用力Fig.4 Moon force on precision centrifuge

由月球对精密离心机的作用力产生的加速度为：

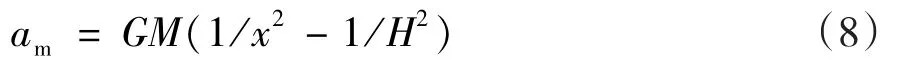
式中：G为万有引力常数；M为月球质量；H为地月中心的平均距离；x为月球中心至精密离心机的平均距离。

由于地月之间的距离远大于地球半径，因此月球对精密离心机的作用力产生的加速度可简化为：

式中：h为地球半径；“±”号表示精密离心机和月球在地球同侧或异侧；加速度am的方向随着月球绕地球的旋转而变化，当am的方向与待标定加速度计的输入轴相同时，加速度计输入轴上感知到的am最大，代入相关数据计算可得此时am的最大值约为1.11×10-6m/s2。一般精密离心机用于加速度计1g以上范围的标校，因此对精度为10-6量级的精密离心机，可以忽略月球作用力对精密离心机的影响。

按照上述原理，同样可计算出太阳对精密离心机的作用力大约是月球对精密离心机作用力的0.45倍。当月球、太阳以及精密离心机处于同一直线上时，月球和太阳对精密离心机的作用力最大，最大作用力产生的加速度不超过1.6×10-6m/s2。因此对精度为10-6量级的精密离心机，可以忽略月球和太阳作用力的影响。但对于更高精度的精密离心机则需要进一步分析月球和太阳作用力的影响。

3 结论

考虑精密离心机中失准角的影响，采用齐次变换建立了加速度计输入轴上感知的科氏加速度数学模型，并对科氏加速度进行了量级分析和简化。计算结果表明必须考虑科里奥利力对加速度相对标准不确定度为10-6量级的精密离心机的影响。此外，计算出月球和太阳对精密离心机的作用合力产生的加速度最大不超过1.6×10-6m/s2。对于精度为10-6量级的精密离心机，可以忽略月球和太阳作用力的影响。

参考文献：

［1］ IEEE Std 836－1991，IEEE Recommended Practice for Precision Centrifuge Testing of Linear Accelerometers［S］.

［2］ 陈岩.精密离心机误差分析与补偿方法研究［D］.哈尔滨：哈尔滨工业大学，2006.CHEN Yan.Study on Error Analysis and Methods of Compensating for the Precision Centrifuge［D］.Harbin:Harbin Institute of Technology，2006.

［3］ 吴付岗，王军.精密离心机加速度载荷模型研究［J］.机械工程学报，2010，46（8）:36－40.WU Fu-gang，WANG Jun.Research on Acceleration Load Model of Precision Centrifuge［J］.Journal of Mechanical Engineering，2010，46（8）:36－40.

［4］ 陈希军，任顺清.加速度计高阶误差模型系数的标定方法［J］.中国惯性技术学报，2010，18（4）:508－512.CHEN Xi-jun，REN Shun-qing.Calibrating Method for High-order Coefficients in Accelerometer Error Model［J］.JournalofChineseInertialTechnology，2010，18（4）:508－512.

［5］ 乔仁晓.加速度计非线性项系数校准误差分析与建模［J］.系统仿真学报，2008，20（6）:1633－1635.QIAO Ren-xiao.Error Analysis and Modeling in Calibration of Accelerometers’Nonlinear Terms’Coefficients［J］.Journal of System Simulation，2008，20（6）:1633－1635.

［6］ 张晶，杨林章.引潮力与潮汐应力对强震触发的研究［J］.地球物理学报，2007，50（2）:448－454.ZHANG Jing，YANG Lin-zhang.A Study on Tidal Force/Stress Triggering of Strong Earthquakes［J］.Chinese Journal of Geophysics，2007，50（2）:448－454.

［7］ 李伟.科里奥利加速度对机械摆的影响［J］.机械工程学报，2003，39（12）:95－98.LI Wei.Influence of Coriolis Accelerate for Pendulum［J］.Journal of Mechanical Engineering，2003，39（12）:95－98.