SPSS统计软件包在矿石小体重回归模型构建中的应用
李 社 ,卢 财
中铝矿产资源有限公司青海分公司,青海西宁 81000
在多金属矿床储量评价工作中,矿石小体重是一个重要参数,也是一项重要内容 ,矿石体重预测的准确与否,将直接影响到矿床的经济评价和矿山储量预测。因此,准确地预测矿石的小体重显得尤为重要。在实际工作中,假如不考虑影响矿石体重的各种因素,进行储量计算时,即利用所测定的小体重的算术平均值来代入储量计算公式求得矿体储量,难免会影响到储量计算结果的可靠程度。相反,如果在每个中段或矿块去测定矿石的小体重,必然耗费大量的人力、物力和财力,进而直接影响到矿床的勘探速度和矿山的生产建设。因此,为了既能节省人力、物力和财力,又能加快矿床的勘探速度和矿山的生产建设,本文利用SPSS的多元回归分析对所测定的矿石小体重与矿石品位进行数学模拟,得出一个有关小体重与品位的多元数学模型,利用该数学模型可以准确的计算每一块段的体重,从而很大程度上提高了资源储量评价的可靠性。
1 SPSS统计软件简介
SPSS(Statistical Product and Service Solutions)是世界上著名的统计分析软件之一,由美国斯坦福大学的三位研究生于20世纪60年代末开发出来的,名为“社会科学用统计软件包”,这是为了强调社会科学应用的一面。实际上,该软件适用于自然科学、社会科学各领域。近几年,已经在我国的社会科学、自然科学的各个领域发挥了巨大作用,受到用户的欢迎。SPSS是一个组合式软件包,它集数据处理、分析和图表,从简单的统计分析到多因素分析等等统计分析方法功能于一身。SPSS使用Windows 的窗口方式展示各种管理和分析数据方法的功能,使用户能够清晰、直观、友好的进行各种数理统计分析。
2 小体重回归模型的构建
2.1 矿石小体重的采集与测定
在同一矿石类型中,根据矿石样品在不同的矿体、矿体的不同部位均匀分布,样品数量不少于30个[10]的原则,即富矿、贫矿兼采和接近平均品位多采的原则,使样品小体重测定结果基本上服从正态分布。在整个勘探期间,对矿体进行了小体重样品的均匀布控。共采集到了170件小体重样品(表3),这些样品具有较好的代表性。
小体重样品的测定是基于阿基米德定律,Au、Pb、Zn品位基于化学方法的测定,并按照国家规范要求抽取一定数量的内、外检样品,以确保加工化验分析质量。
2.2 矿石小体重样品的数学分布
首先从数理统计学的角度对170件矿石小体重样品有一个总体的了解(表1、图1)。

表1 矿石小体重数理统计信息表
首先利用SPSS进行频率密度分析,来研究矿石小体重的统计分布规律(图1)。回归分析要求因变量(小体重)服从或近似服从正态分布,由图2得知:几乎所有各点近似围绕着直线,说明数据呈近似正态分布。
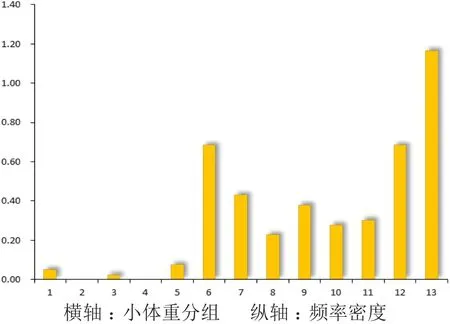
图1 矿石小体重频率密度直方图

图2 矿石小体重正态分布Q-Q检验Pig.2 Normal Q-Q Plot of Smal l Block Weight
2.3 Reg ression分析
多元回归分析在工程技术领域应用,是一种广泛的统计分析方法。因其能够图表化地表征若干随机数值的离散程度、分布状态,正确地反映两组及两组以上变量之间的相互关系,从而使人们掌握这些内在规律, 并从中得到切合我们实际的数学模型,因此它在地质勘探工作中得到了深入广泛的运用,即常用来分析和加工地质资料,进一步保证基础资料的可靠性。
选取小体重样品测试结果作为多元回归分析的基础样本,其中选取小体重(XT)作为因变量,金(Au)、铅(Pb)、锌(Zn)作为自变量进行多元回归分析。本文此次利用SPSS多远回归分析模块采用逐步回归分析(Stepwise)法,通过计算非随机变量的偏回归平方、大小及其显著性检验,按照其重要性逐步选入回归方程,对小体重测试结果与其Au、Pb、Zn的矿石含量的分析结果进行多元回归分析。

表3 方差分析表

表4 回归分析模型系数表
从表3得知:根据方差分析对模型进行显著性检验,其结果(表3)数据表明:回归效果(模型)极为显著,模型可用。从表4同样可以得出,回归模型的各项回归系数,以及对回归系数的显著性检验,即模型的各项系数极为显著。
最终根据表3、4 综合得出,模型及其回归系数均是显著的,即:

(XT 为矿石小体重、Au 、Pb 、Zn分别为品位数值)
可作为最优回归模型,即可用于小体重的预测。通过对比残差与小体重测试容许的关系,说明该模型是否适用于预测小体重,如果残差值<测试容许误差,则模型可用于计算(预测)小体重;否则,需进行更详细的矿石类型划分等,再构建相应模型。
3 结论
1)SPSS软件功能强大、应用广泛、易学易用,对地质工作中,存在大量需要统计分析的问题,运用SPSS软件包中相应的统计分析模块,能够简单快速的得到我们所需要的分析结果,彻底消除了重复、单调的数学运算过程,使地质专业人员拥有更多的时间专注于统计分析模型的构建与分析结果的评判中;
2)构建了矿石小体重与品位之间的数学模型。调用SPSS的Regression模块,对所测定的矿石小体重与其相应品位进行了多元回归分析,构建了矿石小体重与矿石品位之间的数学模型,利用该模型就可以简捷、准确、客观的计算每一个单工程及矿体块段的体重值。从而为资源量估算的可靠性提供了科学依据;
3)在以后的工作中,该模型尚有待于进一步优化,尽可能的、准确的、更客观的耦合矿石小体重与品位之间的相互依存关系。
[1]曹春祥,李能强.小块体重的多元线性回归方程在锡铁山铅锌矿床储量计算中的应用[J].矿产与地质,2005.108(19):177-182.
[2]张景平,李社.2011.基于SPSS的矿石小体重与品位的多元回归分析模型的构建[J].东华理工大学学报(自然科学版),34(1):62-66.
[3]林喜.矿石体重的多元线性回归分析及其检验[J].2010,29(2):157-163.
[4]冯适安.多金属矿床中矿石体重与金属品位的关系[J].湖南地质,1983,2(2):58-61.
[5]王志民.童光煦.1998.人工神经网络在矿石体重回归中的应用[J].中国锰业,16(4):17-18.
[6]吴惠康.用数理统计方法求小块样品体重[J].地质与勘探,1976,04:66-68.
[7]张文彤.SPSS11统计分析教程(高级篇)[M].北京:北京希望电子出版社,2002:64-69.
[8]李英龙,严碧.SPSS统计软件包在矿山统计分析中的应用[J].黄金,2000,21(5):17-19.
[9]何兴江,张信贵等.2006.基于SPSS的城市区域地下水变异Factor Analysis过程[J].地质与勘探.42(1):93-95.
[10]DZ/T0214-2002.铜、铅、锌、银、镍钼地质勘查规范[S].北京:中国标准出版社.
[11]赵鹏大.地质勘探中的统计分析[M].北京 中国地质大学出版社,1990,86-90.
[12]候景儒,黄竞先,等.1982 地质统计学及其在矿产储量计算中的应用[M].北京:地质出版社,23-29.

