储油罐的变位罐容表标定模型的建立与分析

文/刘斯琦

储油罐的变位罐容表标定模型的建立与分析

文/刘斯琦

本文对于储油罐变位识别与罐容表标定问题，运用积分法推导出储油罐内油位高度与储油量的对应关系式，同时依据实验数据进行验证和改进，分析得到罐体变位前后罐容表的数学模型，并利用数值积分的方法求解模型。

储油罐；变位；标定；模型

对于储油罐无变位的情况，运用积分法推导出油位高度与储油量的对应关系式，并利用实验数据进行验证和改进；然后，对于罐体倾斜角为α=4.1的纵向变位的情况，从五个阶段分别建立油位高度与储油量的对应关系式，并根据实验数据对所建立的所有关系式进行检验和改进，最终得到符合实际情况的模型。

1.问题的描述与假设

对于加油站中的地下储油罐，需要采用流量计和油位计来测量进、出油量与罐内油位高度等数据如图1所示，并通过预先标定的罐容表进行计算，进而得到罐内油位高度和储油量的变化情况[1～3]。由于许多储油罐在使用一段时间后，罐体的位置发生变化如图2所示，从而导致罐容表发生改变如图3所示[4～5]。

为便于分析假设储油罐位置变化后不会发生形变，注油口和出油管的体积忽略不计，不考虑温度、压强对储油量容积的影响，将储油罐两端视为平底如图2所示。

图1 储油罐正面示意图

图2 储油罐纵向倾斜变位后示意图

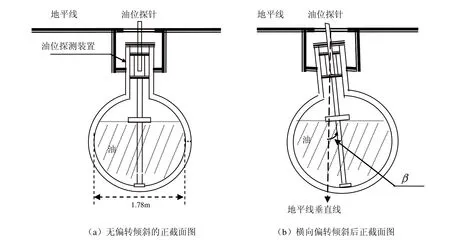
图3 储油罐截面示意图

2.模型的建立

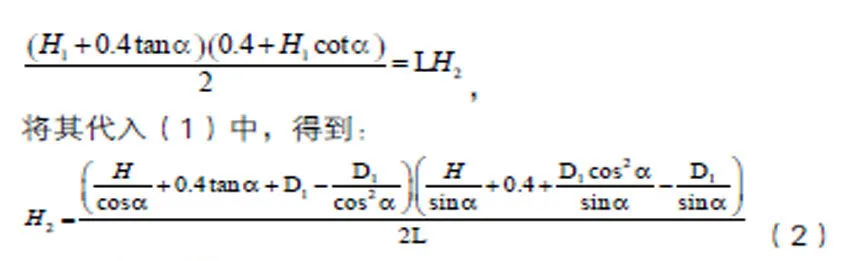
2.1将储油罐倾斜液高H变换为垂直罐底的液高H1，再将H转换为水平状态下的液高H2

利用矩形面积等于梯形面积，可以得出：

2.2小椭圆型储油罐罐体无变位模型建立

（1）罐内油位高度与储油量对应关系模型

小椭圆型储油罐罐体相当于一个椭圆柱体，示意图如下所示：

图4 小椭圆型油罐形状及尺寸示意图

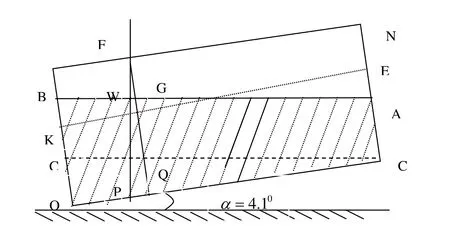
图5 小椭圆储油罐纵向变位时的正面示意图

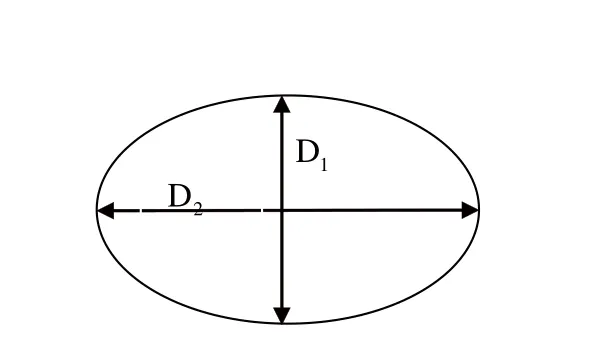
图6 小椭圆油罐截面示意图

图7 小椭圆油罐正面简化图

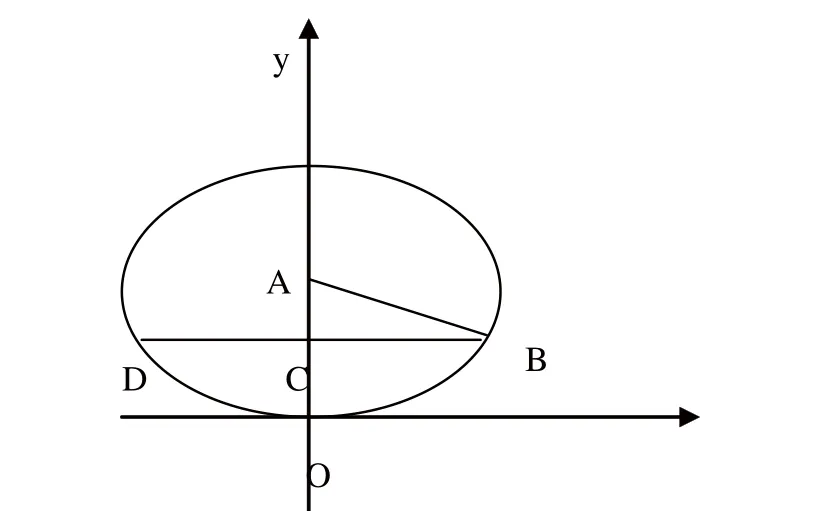
图8 小椭圆油罐切面示意图

通过积分运算得小椭圆油罐内油位高度与储油量的对应关系式为：V=V=πD1D2.

其中，当H=D1时，

式中，D1表示小椭圆油罐截面的长轴长；

D2表示小椭圆油罐截面的长轴长；

L表示小椭圆油罐长度；

H表示小椭圆油罐内的油位高度；

V表示小椭圆油罐车内的储油量；

k表示乘法因子，取0.978。

2.3小椭圆型储油罐罐体倾斜角为α=4.1ο的纵向变位

（1）罐内油位高度与储油量对应关系模型

第一阶段：液面未触及油浮子

由于油位高度H=0，最大储油量为0.008m3，可以忽略不计。因此，不考虑此阶段油位高度与储油量对应关系。

第二阶段：液面触及油浮子，但未没过罐底

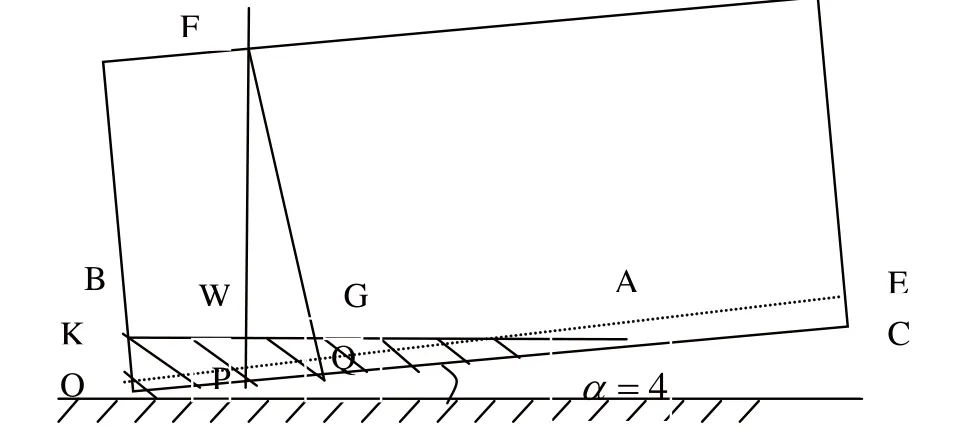
图?9 液面到达C点之前的示意图

该阶段油位高度H的范围为0≤H≤0.18，将（2）式代入（3）式，通过积分运算得到小椭圆油罐内油位高度与储油量的对应关系式为：

式中，D1表示小椭圆油罐截面的长轴长；

D2表示小椭圆油罐截面的长轴长；

L表示小椭圆油罐长度；

k表示乘法因子。

V表示小椭圆油罐车内的储油量；

H2表示在同等储油量的条件下罐体由倾斜状态转换为水平状态后的油位高度；

第三阶段：液面没过罐底，但未触及罐顶

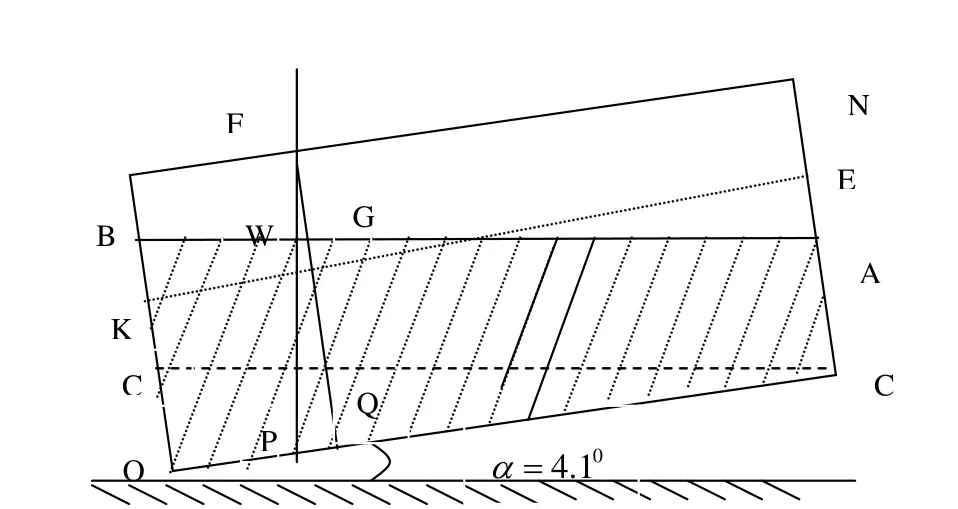
图10 液面到达罐顶前的示意图

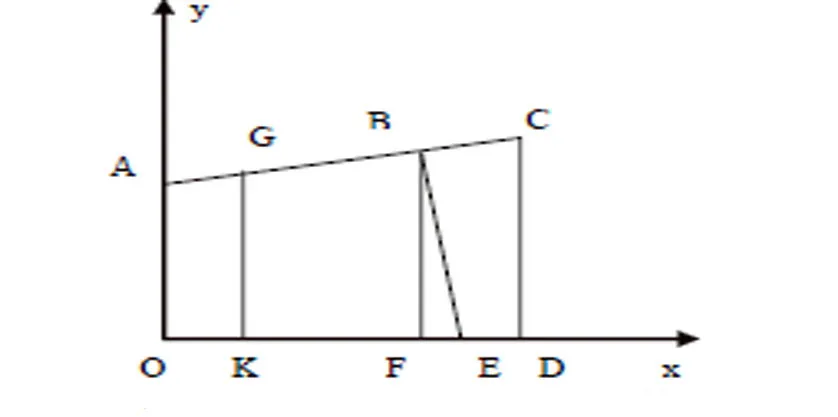
图11 油罐倾斜的正向切面图

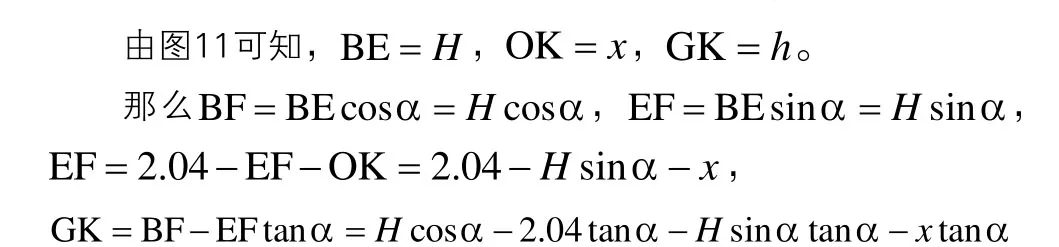
通过积分运算得倾斜角为α = 4.1ο的纵向变位的储油罐内的油量的装载容积公式为

式中，α表示小椭圆型储油罐的倾斜角。

H表示小椭圆油罐内的油位高度；

V表示小椭圆油罐车内的储油量；

D1表示小椭圆油罐截面的长轴长；

D2表示小椭圆油罐截面的长轴长；

第四阶段：液面触及罐顶，但油浮子未达到最高点

由于油位高度H的范围为1.17≤H≤1.2，最大相对储油量为0.007m3，可以忽略不计。因此，不考虑此阶段油位高度与储油量对应关系。

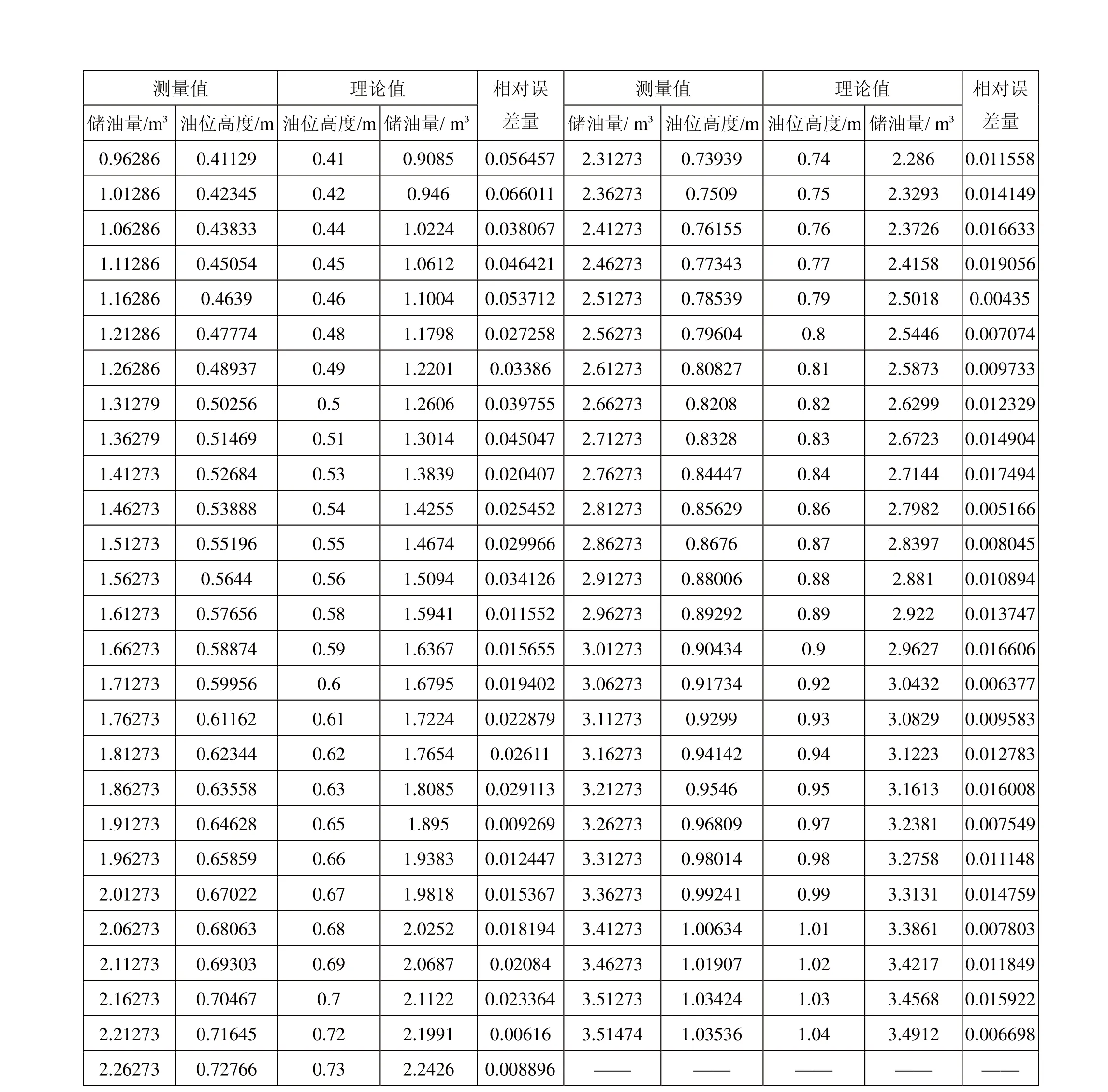
表1 理论值、测量值与其相对误差表

第五阶段：油浮子达到最高点之后

该阶段油位高度为H=1.2，由于该阶段与第二阶段互补，故用总储油量减去第二阶段中的储油量，即可得到该阶段的小椭圆油罐内油位高度与储油量的对应关系式为：

式中，D1表示小椭圆油罐截面的长轴长；

D2表示小椭圆油罐截面的长轴长；

k表示乘法因子；

α表示小椭圆型储油罐的倾斜角；

H2表示在同等储油量的条件下罐体由倾斜状态转换为水平状态后的油位高度；

V表示小椭圆油罐车内的储油量。

3.模型的计算与标定

3.1模型的计算

根据所建立的模型，容易得到某一油位高度所对应的储油量的理论值，并与小椭圆储油罐无变位的实验数据作比较，得到相对误差量，结果如表一所示：

由表1可知，最大相对误差量为0.066011，这表明理论值与实际值相差很少，在误差允许的范围内是可以接受的。

3.2罐容表的标定

根据所建立的模型，计算得出罐体变位后油位高度间隔为1cm的罐容表标定值，具体结果如表二所示：

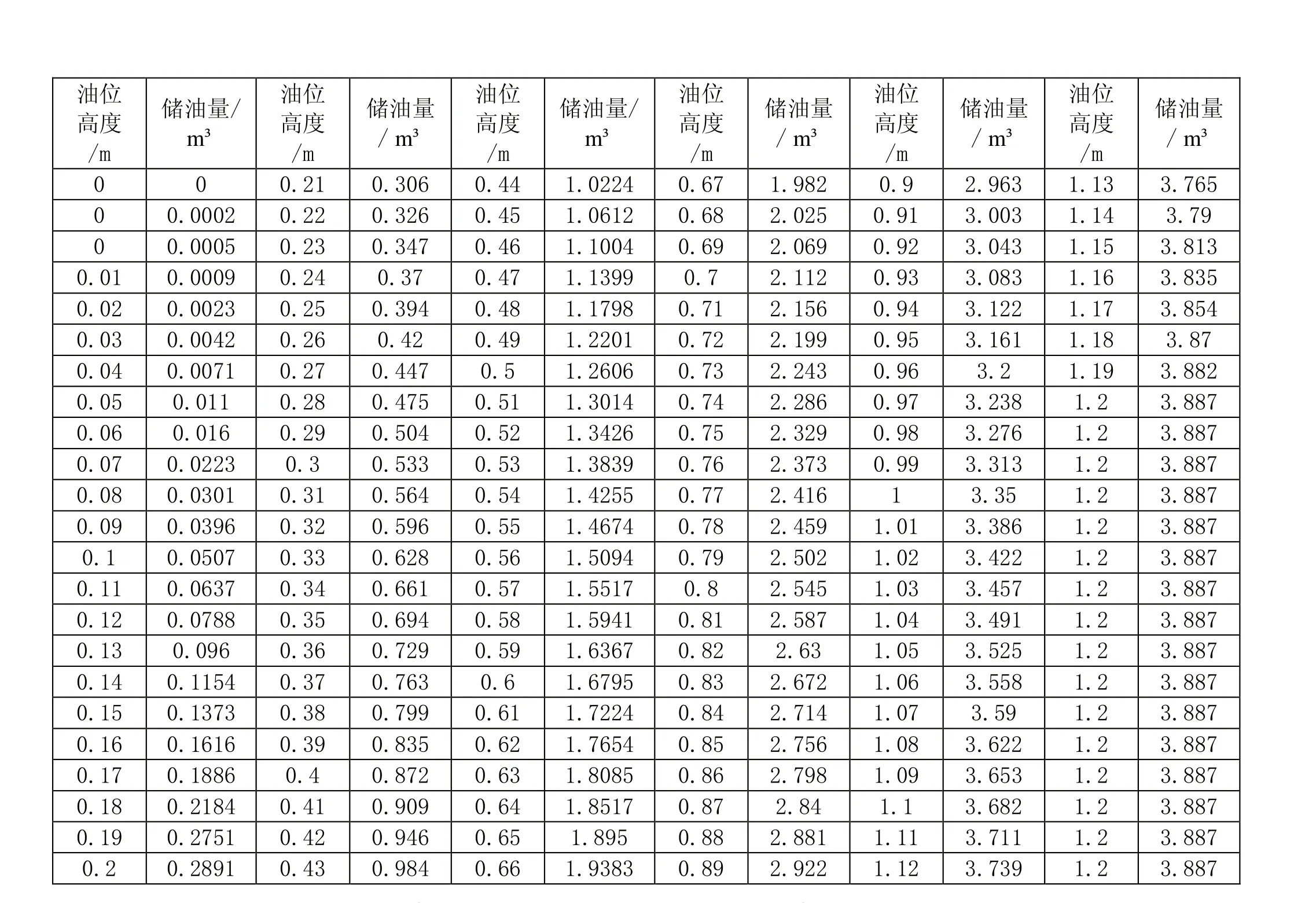
表2 罐体变位后油位高度间隔为1cm的罐容表标定值

4.小结

本文对于储油罐无变位的情况，运用积分法推导出油位高度与储油量的对应关系式；然后，对于罐体倾斜角为α=4.1ο的纵向变位的情况，从五个阶段分别建立油位高度与储油量的对应关系式，并根据实验数据对所建立的所有关系式进行检验和改进，最终得到符合实际情况的模型。对于储油罐变位识别与罐容表标定问题，运用积分法推导出储油罐内油位高度与储油量的对应关系式，分析得到罐体变位前后罐容表的数学模型，并利用数值积分的方法求解模型，对储油罐罐容进行了标定，为研究测量罐容的准确性提供了借鉴。

[1] 严禹卿.椭圆型封头卧罐容积的计算[J]. 炼油设计，1981，1（4）：16～20.

[2] 林成森.数值计算方法[M]. 北京:科学出版社，1981.

[3] 熊小松.椭圆型封头卧罐装载容积与液位关系的计算机实现[J].计算机应用，2004，1（1）：32～45.

78421部队）