考虑换相过电压的三相桥式全控整流电路建模及验证
王海军,霍乾涛,赵绍兴
(国电南瑞科技股份有限公司,江苏 南京 210061)
1 引言
随着社会和科技的发展,电力电子器件在工业中使用的种类和数量规模日趋增多。尤其在电力系统、电气传动和轨道交通等行业中,由可控硅元件构成的三相桥式全控电路作为变流回路的主流拓扑,在行业中使用相当广泛。现代同步发电机励磁系统,基本都采用三相桥式全控整流电路提供励磁电流到发电机转子回路[1]。
三相桥式全控整流电路主要是通过换相整流形式将交流电变成直流电。在换相过程中,快速关断的可控硅内部重新形成PN结时,由于漏抗的存在,在交流端将产生很高的换相过电压。为了保证回路中各元件的安全,一般在可控硅元件的AK极连接抑制回路来限制可控硅换相过电压,保护元器件的安全。
抑制可控硅换相过电压的方式主要有非线性电阻、RC阻容电路等。随着使用年限的增加,非线性电阻存在老化问题,且一般只能限制过电压的幅值,不能降低过电压的上升率。而较高电压上升率的换相过电压可能导致其他处于关断状态的可控硅导通,存在可控硅桥失控的隐患。而RC阻容吸收限制器在限制幅值的基础上可以减缓电压上升率,而且没有荷电率问题,具有较高的可靠性和抑制性能,因此三相桥式全控整流电路一般采用RC回路作为抑制回路限制可控硅换相过电压。
RC回路参数的选取原则包含两个方面:①限制换相过电压在容许范围内;②消耗的功率尽可能小。文献[1]介绍了RC回路参数的设计计算方法并给出了计算实例。文献[2]分析了单个可控硅的反向恢复过程,讨论了反向恢复电流的指数函数模型和双曲函数模型,并给出了RC回路参数的实用计算方法。需要指出的是,按此方法选取的阻容回路参数并不一定是最佳的。
为选取最佳RC参数,需要对换相过程进行模拟。文献[3]用PSPICE仿真软件对单个可控硅及吸收电路进行了模拟,并对RC参数对换相过电压的影响进行了分析。当电容达到一定数值时,进一步增加电容值对减小换相过电压作用不大。对于某个特定电容值,存在使换相过电压最小的电阻值。文献[4]用Matlab/Simulink建立了包含反向恢复过程的可控硅模型,并进行了测试电路和三相交流整流电路的仿真。
本文结合可控硅元件的反向恢复特性和三相桥式全控整流电路及电感性负载的特点进行数学建模,直接用Matlab进行求解,提高了仿真速度,并用实际工程参数和换相过电压波形对仿真结果进行了验证。
2 模型的建立
三相全控桥式整流电路拓扑结构如图1所示。每一个可控硅元件并联一组阻容吸收支路以限制该元件在换相过程中出现的换相过电压。
图1中,T1-T6为可控硅元件,R1-R6、C1-C6分别为阻容吸收回路的电阻和电容。根据电路工作原理可知,可控硅元件T1-T6依次在T1-T6时刻导通,同时在T5-T4依次关断,且周而复始。

图1 三相全控桥式整流电路拓扑结构
对图1电路的建模基于三个方面的考虑:①换相时可控硅元件的关断过程;②交流电源侧的电感;③负载为大电感的感性负载。
2.1 可控硅元件的关断模型
三相全控桥式整流电路在换相时,可控硅元件由于所加的反向电压而被强行关断。由于残留的载流子不能立即消失,在反向电压存在条件下,元件内部将再次形成PN结,导致可控硅内部电流将反向流通,直到电流快速衰减到稳态漏电流值。由于交流电源侧漏电感的存在,此时产生的尖峰脉冲di/dt在回路电感上会产生很高的过电压即换相过电压。文献[2]对反向恢复电流模型作了详细分析,包括突然截止模型、指数模型和双曲正割模型。考虑工程的通用性和精确性选用指数函数模型作为可控硅元件关断模型,如图2所示。
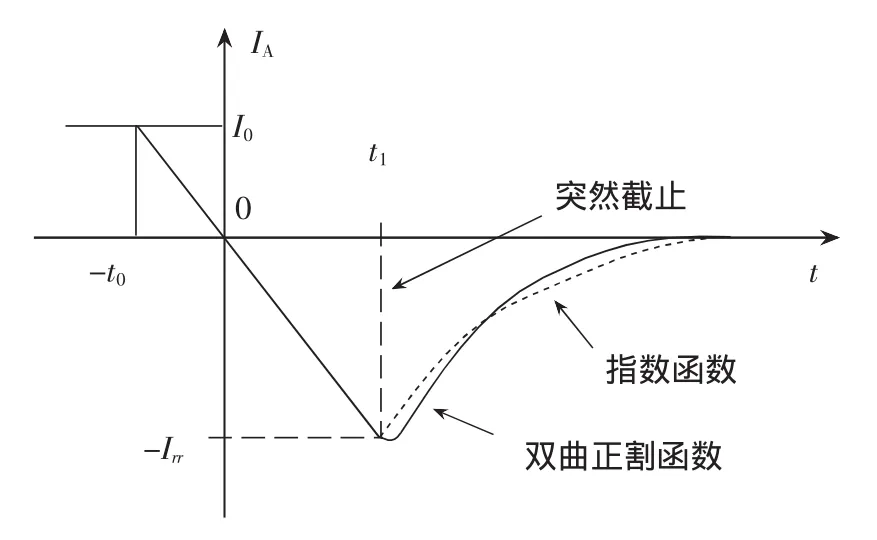
图2 可控硅关断模型示意图
图2中I0为可控硅关断前流过的电流,-t0为可控硅开始换相的时刻(本文取t0>0),Irr为最大反向恢复电流,Qrr为反向恢复电荷,t1为达到最大反向恢复电流的时间。
可控硅反向恢复电流模型可表示为:

2.2 三相全控桥式整流电路数学模型
假设T1为每个周期的开始时刻,该时刻由可控硅的触发角度所决定。因此对于考虑换相过电压的模型,将可控硅关断模型加入每个分段函数即可。
现以T1关断、T3开通为例,建立具有换相过电压的模型。此时T2处于导通状态,由于换相过程十分短暂,且当负载为大电感性负载时,流过c相的电流ic基本不变化,故dia/dt=-dib/dt。由基尔霍夫定律可知:
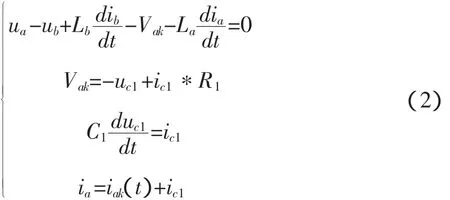
式中:ua、ub、uc分别为不考虑换相过电压的变压器a、b、c相的相电压;La、Lb、Lc分别为变压器a、b、c相的漏感;Vak、uc1分别为关断可控硅AK极两端电压和阻容吸收电容两端电压;ic1为流过电容的电流。
当t≥t1且当iak小于可控硅漏电流后,可控硅T1将处于关断状态。由于可控硅漏电流非常小,因此可忽略为0。因此,当t≥t1且当iak小于可控硅漏电流后式(2)将变为:
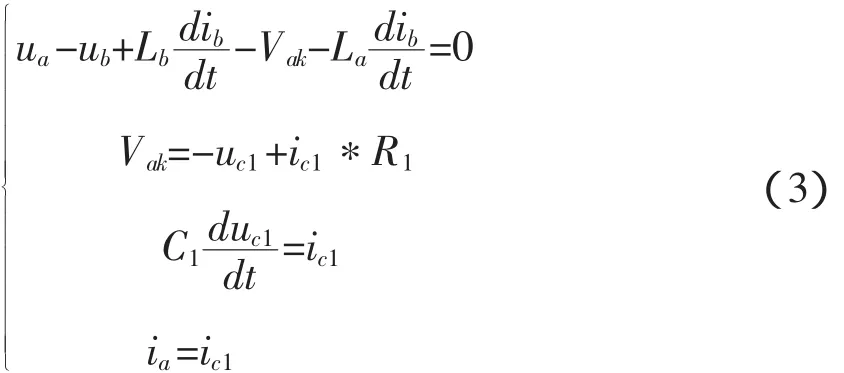
三相桥式全波整流电路交流侧相电压为:

三相桥式全波整流电路输出直流电压为:
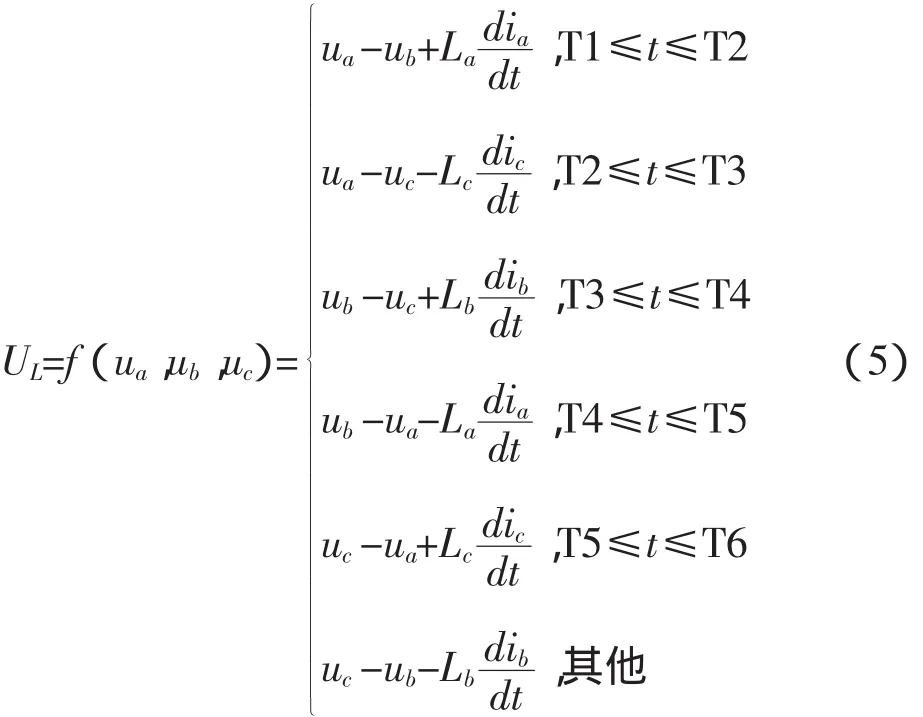
式(1)-(5)完整地表述了考虑换相过电压的三相桥式全控电路模型。该模型可用Matlab直接求解。相对于采用Matlab/Simulink仿真,不需要专用工具箱,从而节省了软件费用。由于不必对每个可控硅元件建模,仿真过程可大大简化,且仿真速度很快。
3 模型的验证
为了验证该模型的正确性,根据上述模型用Matlab进行了仿真,同时将仿真结果与在励磁系统使用的三相全控桥式整流电路的录波进行了对比。
某电厂7号机励磁阳极电压录波波形如图3所示,仿真波形如图4所示。现场测试条件:Uab为额定1024V,触发角为76.8°,直流电流为2878A,R1=20Ω,C1=2.5μF,仿真参数基本与现场测试条件相同,可控硅为T451N型。根据当前运行的参数查可控硅特性曲线可知Irr=527A,Qrr=20.8mAs。

图3 励磁系统录波波形
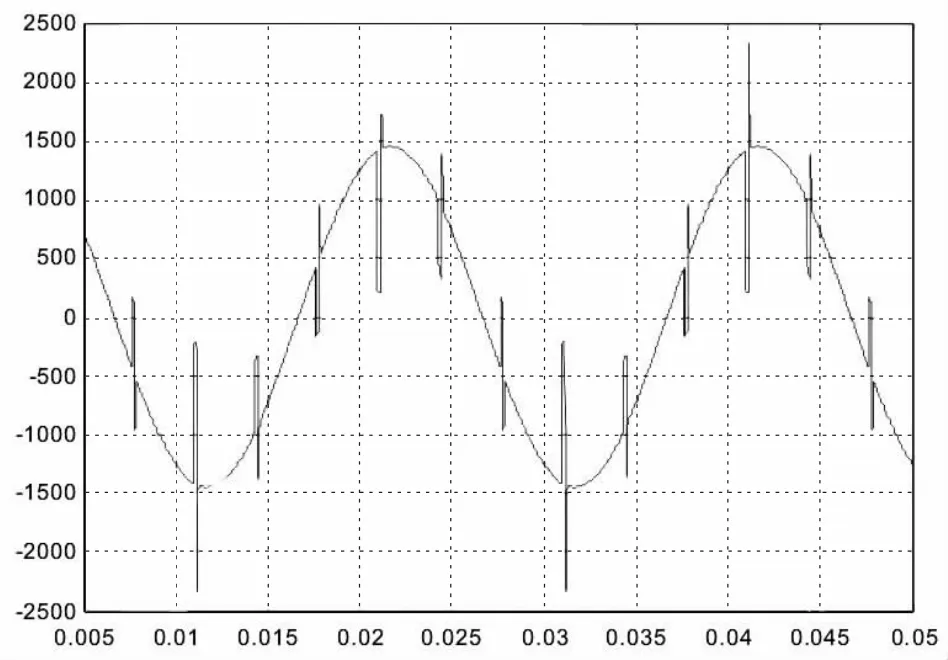
图4 Matlab仿真波形
由波形图可看出其波形基本一致,测量的换相峰值约为2400V,仿真得到的换相峰值幅值为2360V,由于仿真是没有考虑励磁变到可控硅电缆连接的电抗,因此将会产生一部分差异,但是由于换相差异很小,在工程设计时可忽略不计。
4 结论
针对三相全控桥式整流电路可控硅元件的换相过电压问题,通常采用并联阻容电路来限制换相过电压。为选取最佳的阻容参数,建立了考虑换相过电压的三相桥式全控整流电路模型,并通过电厂实例验证了该模型的正确性。
[1]李基成.现代同步发电机励磁系统设计及应用(第2版)[M].北京:中国电力出版社,2009.
[2]JWaldmeyer,BBacklund.Design of RC Circuits for Phase Control Applications.ABB Doc.No.5SYA2020-02,Feb.2008.
[3]张 斌,王 辉,李增印,李全香.基于P-N结反向恢复过程的吸收电路的仿真设计[J].机车电传动,2003(6):27-30.
[4]郝 勇,许其品,曾继伦,吕宏水.可控硅换相过电压的MATLAB仿真[J].水电厂自动化,2007(4):195-199,204.
[5]王兆安,刘进军.电力电子技术(第5版)[M].北京:机械工业出版社,2011.

