汽轮机长叶片弯曲与轴系扭转耦合振动研究

吕方明， 危 奇， 鲁录义， 吕 凯，王 坤， 孙 庆， 李汪繁， 王秀瑾

（1.华中科技大学 能源与动力工程学院，武汉 430074；2.上海发电设备成套设计研究院，上海 200240）

汽轮发电机组轴系是由叶片、轮盘和主轴组成的复杂系统.随着大型汽轮发电机组容量的提高，低压转子末级（或次末级）叶片不断增长，其刚性减弱，固有频率下降，有可能落入较低的主轴扭振频带内，从而使叶片切向振动惯性力能激发其主轴扭振模态，另一方面，主轴扭振惯性力也能激发叶片切向振动，这样就构成了耦合作用系统［1］.这种耦合作用可能使轴系产生共振，进而酿成安全事故.台湾核电三厂900 MW核电机组末级动叶片损坏飞脱事故就是这种原因造成的［2］.国内外研究者对此类问题进行了大量的研究.在传统的研究中［3－4］，一般将耦合作用系统分为主部件转子和分支部件轮盘－叶片系统，分支部件轮盘－叶片系统的各阶模态简化为等效的质量－弹簧系统，如此可以将原来大规模耦合振动系统降阶为低阶等效的小规模耦合振动系统，进而求出其频率和振型.这种方法显然不便用于分析耦合模型中叶片的振动特性［5］.杨建刚等［6－7］提出了一种能够计算叶片－轴耦合系统稳态和瞬态响应问题的阻抗匹配法，研究表明叶片弯曲振动和轴的扭转振动之间具有很强的耦合性，在外界扰动作用下二者会同时被激发出来，但其计算所用几何模型较简单，难以反映汽轮发电机组转子的耦合振动特性.

随着计算机技术的发展，采用有限元法来计算分析大型旋转机械振动特性成为可能.朱德勇等［8－9］采用有限元法建立了汽轮机末级长叶片及整圈叶片的实体计算模型，并分析了叶片的振动特性.朱德勇等［8］认为，与试验研究相比，有限元法具有安全经济、快捷方便和提供数据全面等优点，是今后叶片优化设计及运行可靠性分析研究的重要手段.

目前，采用有限元法计算和分析汽轮机末级长叶片弯曲与轴扭转耦合振动的研究还鲜有报道.笔者建立了主轴和末级叶栅的三维实体模型，采用有限元法分析和计算其振动特性，并通过对比分析叶片－轮盘模型（简称叶－盘模型）、简化轴系模型及叶－轴耦合模型的振动特性，给出了叶片弯曲振动与轴的扭转振动之间的耦合规律.

1 三维实体模型

1.1 叶－盘模型

所用长叶片为汽轮机低压缸末级叶片.该叶片为带搭子（或称鳍子）的弯扭叶片，叶片模型（忽略叶根结构）如图1所示.单叶片材料属性取值为：杨氏模量E＝2.16×1011Pa，泊松比ν＝0.283，密度ρ＝7.77×103kg/m3.

图1 带搭子的长叶片模型Fig.1 Model of the long blade with riser

笔者采用周期性对称建模方法建立了叶－盘模型.将叶片安装在轮毂上，二者刚性连接，不考虑叶根的紧固特性.采用轴的1/n（n为该级叶片个数）作为基本重复扇区进行周期性对称建模［10］.考虑到叶片的实际安装角度，使用图2所示的两组平面沿轴系径向切割，获得包含完整叶片模型的重复扇区，两组平面的空间夹角为3°.这样就获得了叶片和轮毂的重复扇区模型，经周期旋转后得到图3所示的叶－盘模型.

图2 叶片与轮毂Fig.2 Detail of the blade and hub

图3 叶－盘模型Fig.3 The blade－disc model

叶－盘模型中，相邻叶片的搭子之间留有一定的间隙.汽轮机运行时，受离心力作用的叶片上会产生一个扭转恢复力矩.在扭转恢复力矩作用下，相邻搭子发生接触，并在额定转速下使整圈叶片形成连续耦合的系统，增加了系统的刚度，提高了叶片的振动安全性［8］.

叶－盘模型中，叶片搭子之间的细节如图4所示.在建立模型时，搭子之间的最小距离为1.09 mm.为实现实际运行时叶片搭子之间的接触，在计算时对相邻搭子施加面面接触对，并设置其摩擦因数为0.3.下述叶－轴耦合模型也进行了相同的设置.

需要指出，计算时设置面面接触对对叶－盘模型的动频影响显著.其中的原因以及摩擦因数的设置问题将在其他文献中予以讨论，这里不再赘述.

图4 搭子间隙Fig.4 The clearance between risers

1.2 简化轴系模型

采用某汽轮发电机组轴系作为研究对象，其中包括：高中压转子、低压转子（2个）、联轴器（3个）和发电机转子.由于叶片结构较为复杂，而且数量众多，因此在建立三维模型时仅考虑其转动惯量，将其简化为等截面圆环附加在主轴上，通过调整材料密度使其总转动惯量与实际转动惯量一致.这样就建立了一个相对简化的集中质量模型，如图5（a）的原始模型.而原始模型中存在过多的台阶和倒角等细节会给模型网格划分带来极大的难度，需要对模型的这些细节结构进行适当的简化，见图5（b）.

图5 汽轮发电机组轴系模型Fig.5 Shafting model for the turbo－generator set

为保证简化轴系模型的计算精度，应使简化轴系模型各部分的转动惯量与原始模型一致.采用有限元法计算了2个模型的前4阶模态，计算结果见表1.由表1可以看出，2个模型的最大频率相对偏差出现在2阶模态，仅为－3.50%，可以认为上述简化在本文研究范围内是合理可行的.

表1 轴系模态频率对比Tab.1 Comparison of shafting modal frequency between original and reduced model

1.3 叶－轴耦合模型

将图3所示叶－盘模型安装于轴系原末级位置（低压转子2靠近发电机侧）.轴系上仅建立了一组叶栅，其余各级叶栅仍按照前述附加转动惯量等效处理.三维叶－轴耦合模型如图6所示.与前述简化轴系模型不同，叶－轴耦合模型中不仅设置了末级叶栅的转动惯量，而且考虑了叶片的实际柔度.

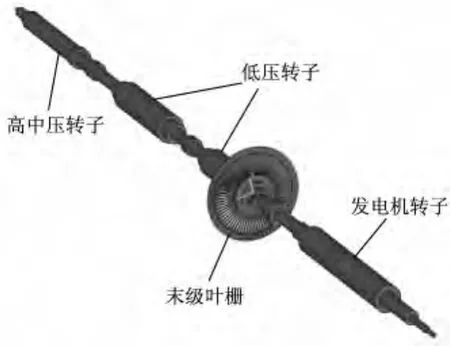
图6 叶－轴耦合模型Fig.6 The coupling model of blade cascade and shafting

上述3个模型（叶－盘模型、简化轴系模型和叶－轴耦合模型）采用了相同的网格划分方法，其有限元网格信息见表2.

表2 有限元网格划分Tab.2 Finite element mesh generation

对3个模型在2种工况下的模态进行计算.工况1：静频（固有频率）分析；工况2：工作转速3 000 r/min下的动态分析.

由于高阶模态下，叶片模态频率数值远大于同阶次轴系扭振模态频率，不在本文分析考虑范围内.因此，这里仅给出叶－盘模型1～3阶模态频率（如表3所示）.需要注意的是，表3中的频率均为叶栅0节径振型时的数据.为避免轴系弯曲振动的干扰，对简化轴系模型轴心所有节点施加3个平移方向固定约束，这样得到的所有振型均为扭振振型.该模型各阶扭振模态频率见表3.叶－轴耦合模型的边界条件与简化轴系模型相同，其各阶模态频率见表3.

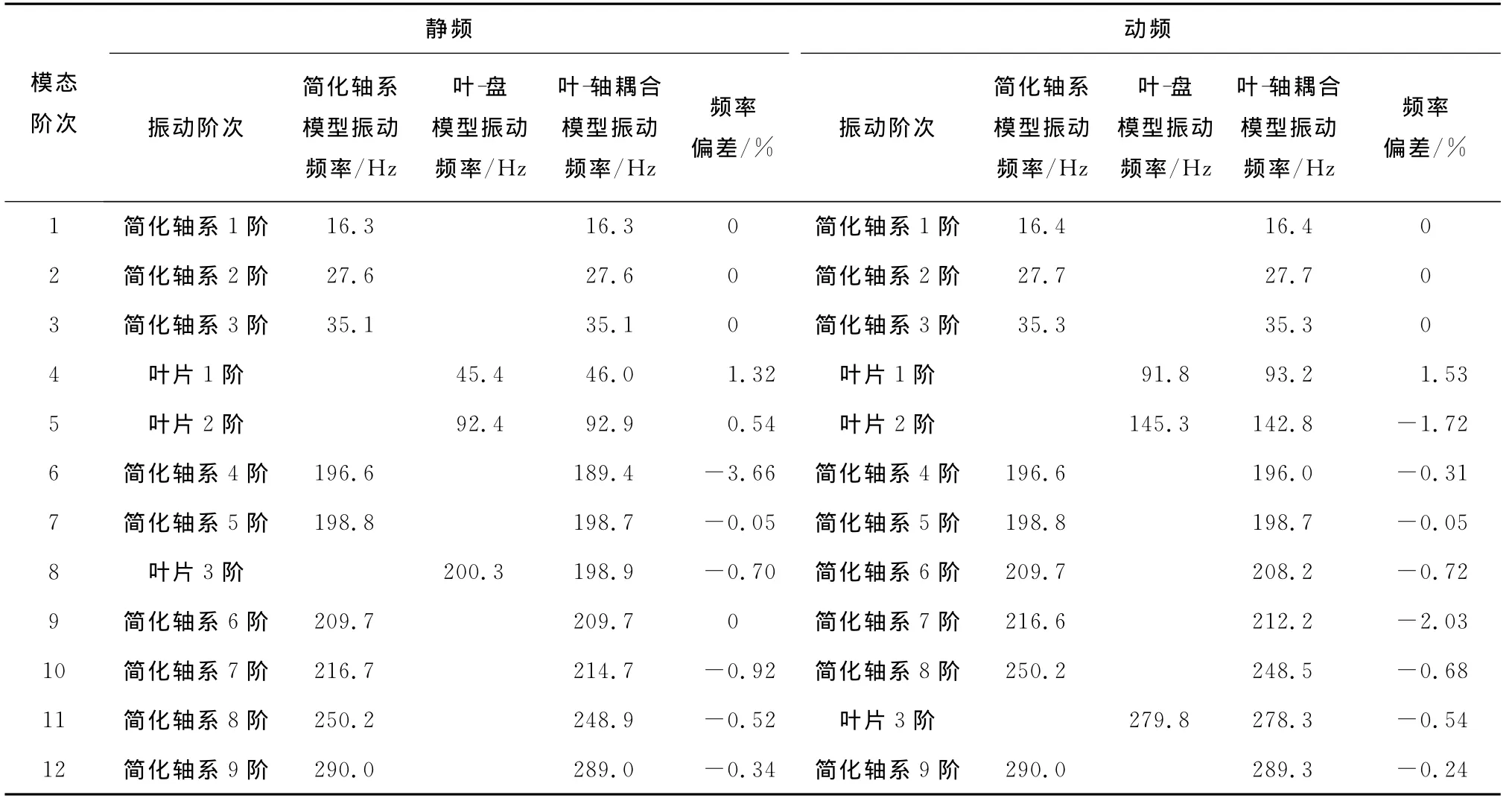
表3 三维模型各阶模态频率的对比Tab.3 Comparison of modal frequency among different three－dimensional models

2 结果与讨论

扭叶片振动时，周向振动和轴向振动同时存在.叶片振动的周向振动分量引起轴的扭振，而轴的扭振又形成叶片的周向惯性力，从而引起叶片振动，二者是以这样的机理耦合在一起的［11］.为便于比较，将叶－轴耦合模型在动、静态工况下各阶轴系振型以及模型中叶片的振动位移示于图7和图8.图7和图8中，横坐标为轴系长度，纵坐标为振动位移（已进行归一化处理）.下面将根据表3、图7和图8中数据进行对比分析.

2.1 叶片柔度的影响

由表3可以看出，多数情况下叶－轴耦合模型振动频率低于简化轴系模型对应阶次的振动频率.如叶－轴耦合模型中，静频的6阶、7阶、10阶、11阶和12阶，动频的6阶、8阶、9阶、10阶和12阶.

由于叶－轴耦合模型考虑了长叶片的柔度，使得整个模型的刚度低于简化轴系模型，从而造成其振动频率下降，这与理论分析是一致的.

2.2 叶片振动模态

由于长叶片的存在，叶－轴耦合模型中出现了以叶片振动频率为主的模态，如静频的4阶和5阶，动频的4阶、5阶和11阶.

这些模态是由于考虑了叶片的实际参数（如转动惯量、刚度和几何结构等）后才出现的，简化轴系模型没有出现这些模态.由图7和图8可以看出，上述模态下，轴扭振的幅度相对较小，而叶片振动幅度较大，由此也说明，上述模态是以叶片振动为主的.

在对轴系振动特性进行分析时，应尽可能建立与实际情况相符的模型，否则可能出现简化轴系模型所不能反映的状况.如上述简化轴系模型振动特性中就没有出现叶片振动模态.

2.3 轴振模态

由表3可以看出，某些模态下，叶－轴耦合模型振动频率与简化轴系模型对应阶次的振动频率基本相同，最大频率偏差＜0.1%，将这些模态称为轴振模态.如叶－轴耦合模型中静频的1阶、2阶和3阶，动频的1阶、2阶和3阶.

图7 静态工况下叶－轴耦合模型轴振振型Fig.7 Vibration modes of shafting in the coupling cascade－shafting model under static conditions

图8 动态工况下叶－轴耦合模型轴振振型Fig.8 Vibration modes of shafting in the coupling cascade－shafting model under dynamic condition

由图7和图8可见，上述模态下，叶片所在轴段振型基本为水平线，说明该轴段相同半径表面扭振位移基本相同，而叶片变形较小，其周向振动的能量不足以干扰轴的振动，此时叶片振动对轴振频率影响非常小.

振型图也可以说明上述模态下叶－轴耦合模型的振动是以轴振为主的.图9为在静态工况下叶－轴耦合模型与简化轴系模型前三阶振型的对比图.由图9可以看出，虽然使用了不同的线形标明各模型在前三阶模态下的振型，但是2种模型对应阶次的振型几乎完全重合，说明叶片振动对轴的扭振幅值几乎没有影响.

2.4 耦合模态

在表3中，简化轴系模型5阶模态频率与叶－盘模型3阶模态频率非常接近静频，分别为198.8 Hz和200.9 Hz.在叶－轴耦合模型中出现了2个频率非常接近的模态，分别为7阶模态（频率为198.7 Hz）和8阶模态（频率为198.9 Hz）.由图7和图8可见，叶－轴耦合模型7阶和8阶模态下，叶片振幅与轴振幅值大小相当，这与前述叶片振动模态和轴振模态均不相同.因此，认为叶－轴耦合模型的7阶和8阶模态（静频）是叶片弯振与轴扭振共同作用的结果，这种情形与文献［12］中描述一致，称之为耦合模态.

图9 振型对比（静态工况）Fig.9 Comparison of vibration modes（static condition）

图10为简化轴系模型5阶模态振型与叶－轴耦合模型7阶、8阶模态振型的对比，图中竖直虚线表示末级叶栅所处位置.由图10可以看出，叶栅左侧（汽轮机侧）振型曲线变化趋势相同，振幅存在一定差别；叶栅右侧（发电机侧）振型曲线存在较大差别：简化轴系模型5阶模态振型与叶－轴耦合模型8阶模态振型曲线走势相同（同相位），而与叶－轴耦合模型7阶模态振型曲线走势相反（反相位），并且其振动幅值较后二者为小，说明耦合模态下叶片振动对轴的扭振有加强作用.

图10 耦合模态Fig.10 The coupling modes

2.5 叶片振动特性

由表3可以看出，与叶－盘模型相比，受轴系扭振影响，在某些模态下叶－轴耦合模型中叶片模态频率增大，如静频的4阶、5阶和动频的4阶；而在另外几个模态下其频率降低，没有显著的规律可循.在动态工况下，其频率增大或减小的程度更加剧烈.例如，叶－盘模型2阶模态动频为145.3 Hz，由于受轴系扭振影响，叶－轴耦合模型中叶片频率降低为142.8 Hz.与叶－盘模型不同，叶－轴耦合模型中叶片的弯曲振动必然会受到轴系扭振的干扰.

叶片模态振型变化也可以反映轴系扭振对叶片振动的影响.图11为叶－盘模型和叶－轴耦合模型中叶片周向位移的对比，图中横坐标为叶片模型节点到转子轴心的距离，纵坐标为叶片周向振动位移.2种模型中所选叶片节点到转子轴心的距离是对应相等的.

图11 叶片模态振型比较Fig.11 Modal curves comparison of blades

由图11可以看出，2种模型中叶片的振型基本一致，振动幅度相差不大，说明轴的扭振对叶片的周向振动有一定影响，但这种影响并不大.需要特别说明的是图11（c）中叶－盘模型3阶与叶－轴耦合模型8阶模态振型的对比：二者变化趋势基本一致，但位移幅度存在较大偏差.这是因为叶片与轴系刚性连接以后，其振动的部分能量被轴的扭振所消耗，降低了叶片自身的振动幅度.

需要指出，根据本文计算结果得出的上述结论仅适用于本文所述模型，改变计算模型后可能得出不同的结论.另外，受计算规模限制，笔者没有考虑叶根与轴的动态耦合，且仅建立了1级末级叶栅模型.这样建立的计算模型，其振动特性的计算精度可能会与实际情况存在一定差别.但上述规律性结论是可靠的，对汽轮发电机组轴系安全设计仍具有一定的指导意义.而且，本文所述机组低压缸具有4级末级长叶栅，其转动惯量对轴系扭转振动的影响更加复杂，将在未来的工作中深入研究.

3 结 论

（1）与简化轴系模型相比，叶－轴耦合模型存在3种类型的振动模态，即叶片振动模态、轴振模态和耦合模态.叶片振动模态下，叶片振幅较大，轴振振幅较小，而简化轴系模型中不存在该模态；轴振模态下，叶片振幅较小，轴振振幅较大，而且其振型与简化轴系模型几乎完全相同.当叶－盘模型与简化轴系模型振动频率接近时，在叶－轴耦合模型中出现耦合模态，这是叶片弯振与轴扭振共同作用的结果.

（2）受轴扭振的影响，叶－轴耦合模型中叶片振动特性与叶－盘模型中叶片振动特性相比存在一定的差别：叶片振型基本保持一致，但周向位移略有不同；有的模态下振动频率增大，而有的模态下振动频率减小，动频变化幅度较大.从叶片安全角度考虑，设计时应同时考虑其静频和动频，并以叶片振动特性为基础，着重考虑叶－轴耦合时的振动特性，以避开工频波动可能带来的危害.

［1］任福春，杨昆，宋之平.大型汽轮发电机组轴系扭振耦合问题［J］.华北电力大学学报，1996，23（3）：30－35.REN Fuchun，YANG Kun，SONG Zhiping.Couple problems in torsional vibration of large turbine－generator shaft system ［J］.Journal of North China Electric Power University，1996，23（3）：30－35.

［2］许楚镇，张恒涛.汽轮发电机组轴系扭振事故剖析和技术开发展望［J］.动力工程，1990，10（2）：9－14.XU Chuzhen，ZHANG Hengtao.An analytical review of torsional vibration failures of turbine－generator shafting system abroad and in China with a prospect of future development［J］.Power Engineering，1990，10（2）：9－14.

［3］郭力，朱均.汽轮发电机组转子－轮盘－叶片系统耦合扭转振动研究［J］.汽轮机技术，2001，43（4）：226－228.GUO Li，ZHU Jun.The coupled torsional vibrations research of rotor－blade disk－vane system in steam turbine［J］.Turbine Technology，2001，43（4）：226－228.

［4］鲍文，王西田，于达仁，等.300 MW汽轮机低压缸末级长叶片与轴系扭振的耦合振动［J］.汽轮机技术，2000，42（2）：65－68.BAO Wen，WANG Xitian，YU Daren，et al.The coupling of the long blades at the final stage of the low pressure turbine with the shaft torsional vibrations［J］.Turbine Technology，2000，42（2）：65－68.

［5］郭力.汽轮机叶片弯曲与轴系扭转联合振动研究［J］.汽轮机技术，2000，42（4）：218－221.GUO Li.Union vibration research of both vane winding and shafts torsion in turbine［J］.Turbine Technology，2000，42（4）：218－221.

［6］杨建刚，谢东建，高亹.汽轮发电机组叶片－轴耦合系统动力响应问题研究［J］.机械工程学报，2001，37（7）：56－60.YANG Jiangang，XIE Dongjian，GAO Wei.Response calculation and analysis of the coupled blade bending shaft torsion vibration of turbo generator［J］.Chinese Journal of Mechanical Engineering，2001，37（7）：56－60.

［7］杨建刚，高亹.大型旋转机械叶片－轴弯扭耦合振动问题的研究［J］.动力工程，2003，23（4）：2569－2573.YANG Jiangang，GAO Wei.Research on the coupled blade－bending and shaft－torsion vibration of rotating machinery［J］.Power Engineering，2003，23（4）：2569－2573.

［8］朱德勇，姜华伟，高建强.超超临界汽轮机末级叶片的振动特性研究方法［J］.发电设备，2009，23（1）：20－22.ZHU Deyong，JIANG Huawei，GAO Jianqiang.Study methods for vibration characteristics of last stage blades of ultra supercritical steam turbines［J］.Power Equipment，2009，23（1）：20－22.

［9］樊庆林，韩万金.单叶片强度分析及整圈叶片动频计算［J］.汽轮机技术，2007，49（5）：335－337.FAN Qinglin，HAN Wanjin.Analyses of the single blade strength and calculation of the circle blade dynamic frequency［J］.Turbine Technology，2007，49（5）：335－337.

［10］付娜，王三民，郭伟超.某燃气轮机叶片－轮盘耦合振动特性研究［J］.汽轮机技术，2005，47（5）：362－364.FU Na，WANG Sanmin，GUO Weichao.Calculation of the blade－disc coupled vibration characteristics of a gas turbine［J］.Turbine Technology，2005，47（5）：362－364.

［11］OKABE A，OTAWARA Y，KANEKO R，et al.An equivalent reduced modelling method and its application to shaft－blade coupled torsional vibration analysis of a turbine－generator set［J］.Proceedings of the Institution of Mechanical Engineers，Part A：Journal of Power and Energy，1991，205（3）：173－181.

［12］刘英哲，傅行军.汽轮发电机组扭振［M］.北京：中国电力出版社，1997.