去除趋势项时域修正算法在振动速度信号处理中的应用
赵 宁 李建鹏 张 冉 刘春阳
(胜利油田技术检测中心,山东 东营 257000)
0 引言
在振动测试中,由于传感器和放大器温度随环境变化,从而造成零点漂移、传感器频率范围外的低频性能的不稳定以及传感器周围的环境干扰,往往会偏离基线,甚至偏离基线的大小还会随时间变化,这个偏离基线的大小随时间变化的现象就是所谓的趋势项。
1 趋势项对积分的影响
所测的加速度信号中含有直流分量和大量的干扰噪声,例如构造一个信号f(t)=sin(100πt)+0.1,该信号固有频率为50Hz,采样频率为4000Hz,直流分量为0.1,按Simpson(辛普森)计算公式积分,得到的速度曲线如下图所示。

图1 未去除趋势项一次积分曲线
导致这种现象的原因是信号中的直流量并没有完全去除干净,而导致直流量产生的原因主要有两个方面:一是,对信号没有整周期采样,不能正负抵消,采样后计算其累加和并平均到每个点上从而产生误差;二是,A/D变换过程中的量化和离散误差的存在。
2 趋势项的消除
为了消除上述误差,就需要去除信号中存在的趋势项,常用消除趋势项的方法为多项式最小二乘法[1]。其原理如下:
设实际测得振动信号的采样值为 {xk}(k=0,2,3,…,n-1),设多项式函数……(1),其中 k=0,2,3,…,n-1,确定函数 xk的各待定系数 bj(j=0,1,2,…,m),使得函数与离散数据xk的误差平方和为最小,即求……(2)的极值。利用偏导求极值的方法,满足E有极值的条件为其中 i=0,1,2,…,m,依次取 E 对 b求偏i导,可以产生一个m+1元线性方程组:解方程组(4),可以求出m+1个待定系数bj(j=0 ,1,…,m )。 在上式中,j为设定的多项式阶次,其值范围为0≤j≤m。在(4)式中当m=0时,有,即这时求得的趋势项为常数,故当m=0时的趋势项为信号数据的算术平均值。当m=1时为线性趋势项,当时m≥2,这时为曲线趋势项。
误差δ在积分运算中被逐渐放大,使得一次积分后的速度信号含有一次趋势项 (Ct+D)。 因此速度信号的表达式为

表1 速度信号的时间序列
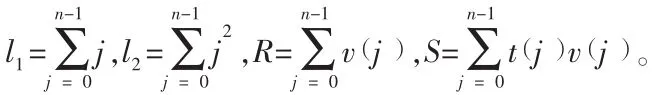
上述信号经过积分后并消除趋势项所得的一次积分如下图所示。
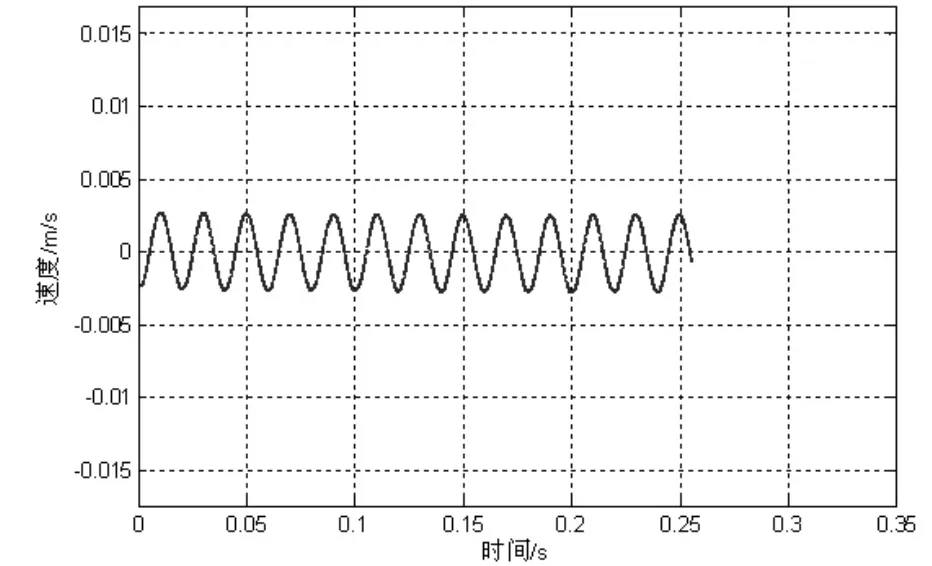
图2 去除趋势项后一次积分结果
3 结论
(1)振动测试中加速度传感器采集的信号含有直流分量和大量的干扰噪声,从而导致经过数字积分得到的速度信号有趋势项。
(2)通过采用最小二乘法的时域修正算法去除了趋势项,得到了准确的振动速度曲线。
[1]高品贤.趋势项对时域参数识别的影响及消除[J].振动、测试与诊断,1994(02).

