水位下降对沿湖路堤边坡渗流特征及稳定性的影响

何忠明 ，史振宁，付宏渊，曾铃

(1. 长沙理工大学 特殊环境道路工程湖南省重点实验室，湖南 长沙，410114；2. 长沙理工大学 交通运输工程学院，湖南 长沙，410114；3. 长沙理工大学 土木建筑学院，湖南 长沙，410114)

在我国区域经济发展、沿湖经济圈逐渐形成的大背景下[1-2]，沿湖公路里程日益增加，环湖区域企业规模与居民数量也随之迅速增加，路堤边坡一旦处于失稳状态，将会对沿湖居民生命及财产安全产生巨大威胁[3]。水位波动是引起边坡失稳的最主要原因[4]。从地质状况角度分析，沿湖地貌普遍为1 级堆积阶地，公路路线多覆盖淤泥质土层[5]，其稳定性对地下水位变化十分敏感。在相同水位下降条件下，饱和淤泥质边坡的稳定系数下降率是砂质边坡稳定系数下降率的3倍以上[6]。从渗流角度分析，湖水对路堤的浸泡导致其内部基质吸力降低，当湖水位下降时，基质吸力在短时间内提升较慢，而外部水压力对边坡土体产生的浮力迅速减小[7]，从而造成路堤边坡失稳。由此可见，从渗流特性角度出发，对水位升降条件下的路堤稳定性进行研究具有重要意义。目前，针对水位变化对库岸岩质边坡稳定性分析成果较多，但综合考虑饱和与非饱和状态下渗流特性对边坡稳定性影响的研究较少，对沿湖路堤在湖水位下降条件下的渗流特性及其边坡稳定性变化趋势的分析更少。在针对岩质边坡的研究中，王思长[8]考虑滑动体底部结构面饱水状态下渗水压力对滑动体稳定性的影响，但在滑动面同时通过饱和区域与非饱和区域时，其理论并不能很好地解释滑动体稳定性的变化规律。尚义敏等[9]采用塑性理论，得到边坡潜在破坏模式为后缘出现张拉屈服破坏和中下部剪切屈服破坏，但此种分析涉及参数较复杂，并不适用于工程实践。基于以上原因，本文作者采用Geo-Studio 有限元软件对沿湖公路在水位下降过程中的渗流特性进行定量分析，并在此基础上分析不同路堤填筑形式、不同水位下降速率下沿湖路堤稳定性系数变化规律，以便为沿湖路堤建设及水位变化条件下的沿湖路堤稳定性预警提供参考。

1 非饱和状态边坡稳定性计算理论

1.1 非饱和土渗流计算理论

沿湖路堤在水位下降过程中，由于路堤上部填土释水的滞后效应以及土体的毛吸作用，其内部会出现非饱和区域。本文考虑路堤内部呈二维非饱和状态，水体积不可压缩。非饱和渗流偏微分方程[10]为

式中：h 为水头高度(m)；Kx和Ky分别为土体在水平方向与竖直方向的渗透系数(m/d)，在计算中仅考虑Kx=Ky；n 为孔隙率(%)；Sw为饱和度(%)；t 为时间(d)。

van Genuchten[11]基于Mualem’s Model 提出的非饱和土渗透系数确定方法，土体中某一区域的渗透系数与其体积含水率有密切联系，将式(1)中Kx和Ky分别表示成体积含水率θ 的函数式Kx(Θ)和Ky(Θ)，即

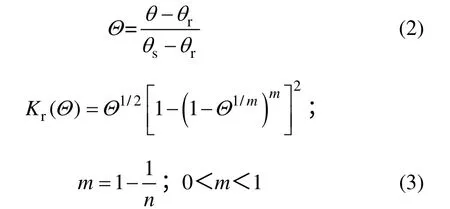
式中：θ，θr和θs分别为体积含水率、残余含水率、饱和含水率(单位均为cm3/cm3)；α，m 和n 为水土特征曲线形状参数。黏土体积含水率、渗透系数与基质吸力的关系见图1，其中饱和含水率与饱和渗透系数参考表1 中土体的物理参数。

1.2 双独立变量定义的抗剪强度理论

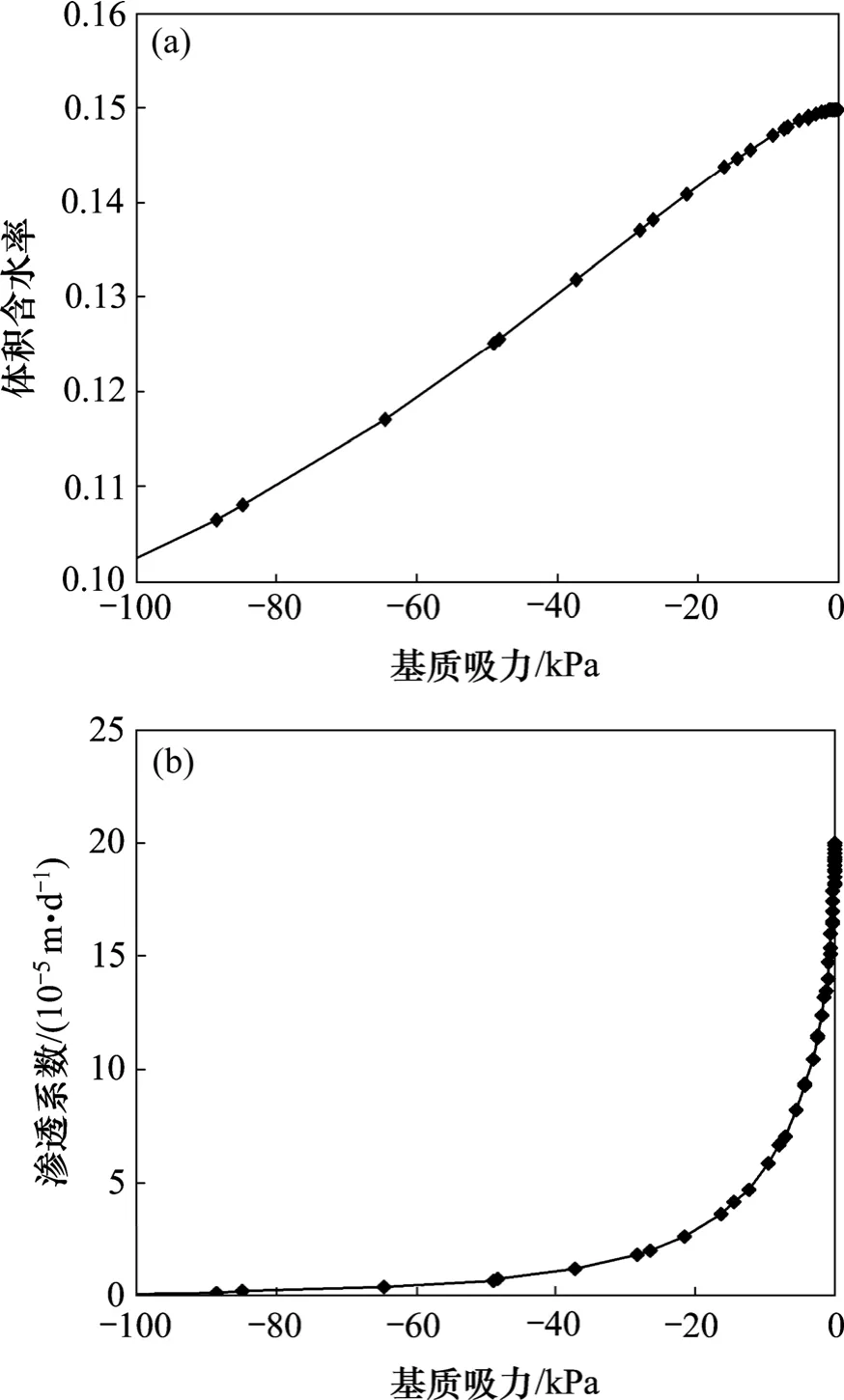
图1 黏土体积含水率、渗透系数与基质吸力的关系Fig.1 Relationship among volume water content,conductivity and matrix suction

在湖水位下降过程中，路堤内部饱和区与非饱和区存在状态较复杂，潜在路堤边坡滑动面必定与饱和区、非饱和区均有相交，而当潜在滑动面通过非饱和区域时，在计算过程中需考虑非饱和土的抗剪强度。

采用一般极限平衡法计算边坡稳定性时，仅考虑土条在饱和状态下圆弧剪切面上的抗剪强度，而并未考虑土体在非饱和状态下破裂面抗剪强度的变化，即无法根据土体中的孔隙气压力与孔隙水压力对抗剪强度的影响分析其边坡稳定性。本文采用基于双独立变量定义的抗剪强度理论对边坡稳定性进行计算。

Ho 等[12]提出的非饱和土抗剪强度公式为

式中：τff为非饱和土抗剪强度；c'为有效黏聚力(kPa)；σf为总应力(kPa)；ua为孔隙气压力(kPa)；uw为孔隙水压力(kPa)；φ′为与静法向应力状态变量(σf-ua)f有关的内摩擦角；φb为抗剪强度随基质吸力(ua-uw)f而增加的速率，本文根据Ho 等[12]对黏土进行常含水量三轴试验得到的结果，取φb=21.7°。式(4)已在非饱和土及相关领域计算中得到广泛应用。

将非饱和土抗剪强度公式引入一般极限平衡法中可得[13]

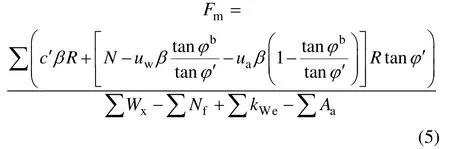
式中：β 为土条宽度(m)；x 为土条重心距滑动面圆心距离(m)；Wx为土条重度(kN)；Nf为土条滑动面法向应力对土条产生的滑动力矩(kN·m)；R 为滑动圆弧半径(m)；Aa为外部水位推力对滑动体产生的抗滑力矩(kN·m)；kWe为作用在土条上的横向力对土条产生的滑动力矩(kN·m)；Fm为考虑力矩平衡的边坡安全系数，Fm采用迭代计算；F 为预设边坡安全系数。

其中：α 为土条底部与水平面夹角。

2 边坡渗流特性有限元计算与分析

2.1 计算模型、参数及边界条件

为研究沿湖路堤在湖水位下降过程中的渗流特性，建立路堤计算模型。本文仅给出边坡坡率为1.0:1.5时路堤模型网格，共划分为316 个节点和282 个单元，特征点位置如图2 所示。

由于在渗流计算与分析中着重对边坡内部孔隙水压力变化状态进行研究，故按照不同水位状态下土体饱和度选取特征点，具体位置如图2 所示。特征点1位于初始浸润线上部，距坡面约1 m，坐标为(13.6 m，8.7 m)，计算过程中均处于非饱和状态；特征点2 位于初始浸润线下部，距坡面约1 m，坐标为(17.0 m，6.3 m)，水位下降过程中由饱和状态转变为非饱和状态；特征点3 位于地基下部1 m 处，坐标为(24.0 m，4.0 m)，水位下降过程中均处于饱和状态。

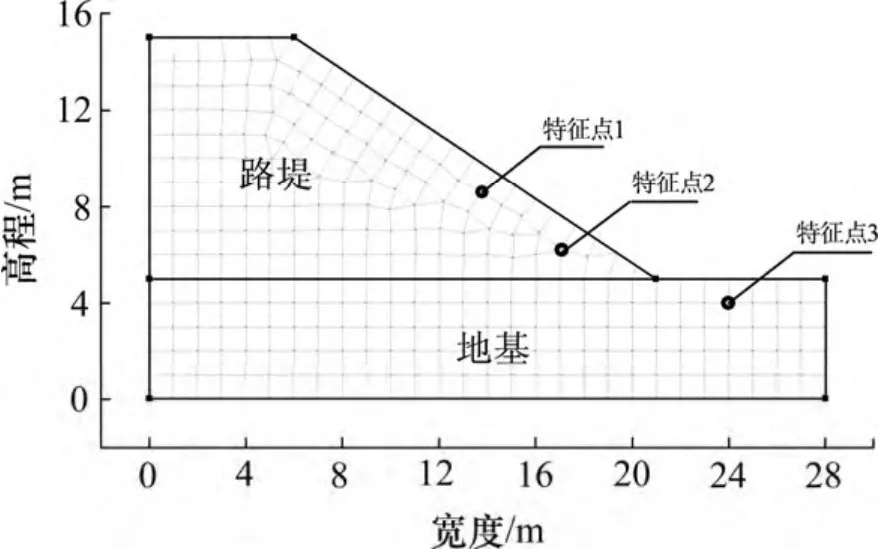
图2 坡率为1.0:1.5 时路堤模型网格划分与特征点位置Fig.2 Embankment model and mesh when slope ratio is 1.0:1.5

根据文献[14]提供的参数范围，路堤填土及地基土物理参数取值如表1 所示。同种土质各处物理性质相同，不考虑其各向异性。非饱和土渗透系数采用式(2)与式(3)进行拟合。由于地基土常年处于湖水位以下，认为其始终处于饱和状态，渗透系数保持不变。

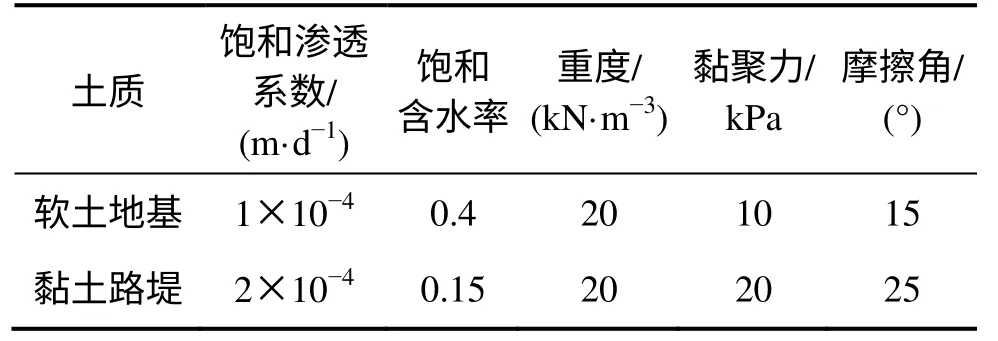
土质饱和渗透系数/(m·d-1)饱和含水率重度/(kN·m-3)黏聚力/kPa摩擦角/(°)软土地基 1×10-40.4 20 10 15黏土路堤 2×10-40.15 20 20 25

初始条件设定如下：湖水位为9 m；总水头如图3所示；路堤边坡9 m 以上部分设置为0 m 水头。边界条件设定如下：采用水位下降速度v 为0.10，0.25 和0.50 m/d 这3 种湖水位下降状态作为水位边界条件，设定路堤左、右侧边界x 方向无位移，底部边界x 和y 方向无位移作为位移边界条件。时间步长为1 d，计算总时长为8 d。设置计算最大迭代次数为50，迭代误差小于1%，计算显示当迭代次数大于2 时其计算误差均小于设定值，即达到收敛状态。

2.2 路堤非饱和渗流特性分析

本文仅列出初始水位状态与水位以v=0.50 m/d 速率下降8 d 后路堤内部孔隙水压力分布，如图3 和图4所示。对比图3 和图4 可知：路堤坡面区域孔隙水压力随湖水位下降明显降低，相对路堤坡面较高位置而言，坡脚处孔隙水压力下降更显著，而路堤内部孔隙水压力随水位下降并无明显变化。

呈现以上变化规律的原因在于：在初始状态下，路堤浸润线以下为饱和状态；随着湖水位的逐渐下降，饱和区域释水形成非饱和区，土体内部体积含水率逐渐减小。由渗透系数与体积含水量的关系可知：当土体由饱和状态变化为非饱和状态时，体积含水率逐渐减小，渗透系数迅速下降，从而减缓路堤内部孔隙水的渗出。对于饱和状态的坡脚部分，渗透系数保持不变，外部水位变化引起路堤内部水体迅速渗出，导致其孔隙水压力产生较大变化。

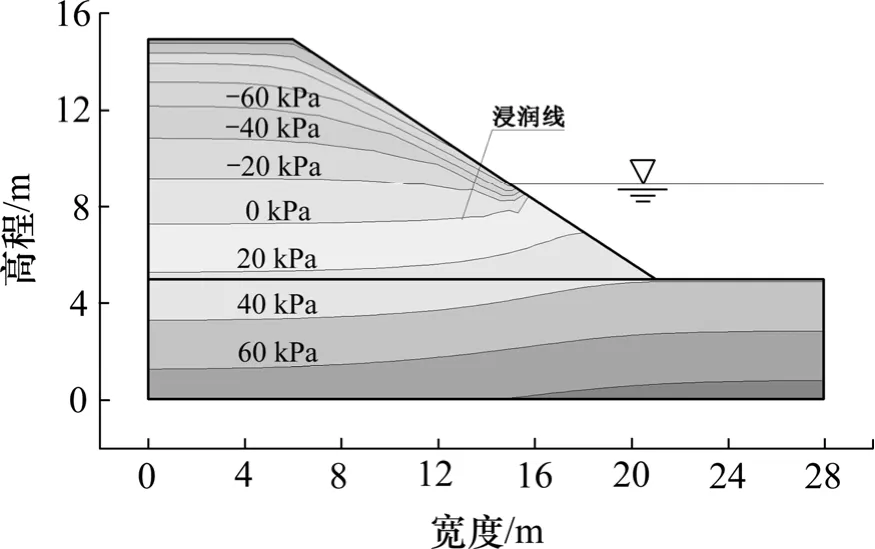
图3 初始状态孔隙水压力分布Fig.3 Pore water pressure distribution of initial state

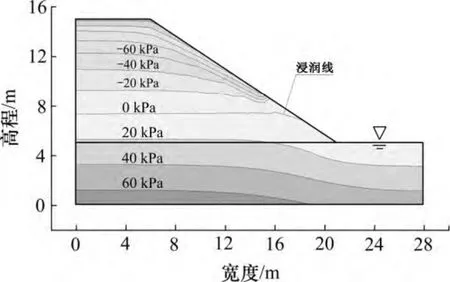
图4 8 d 后孔隙水压力分布图Fig.4 Pore water pressure distribution after 8 d

文献[15-17]表明孔隙水压力的降低幅度主要是由水位降低幅度决定的，但在实际工程中难以准确预测外部水位的最终高度，而水位下降速率容易测量，故在水位下降过程中可采用水位下降速率对路堤内孔隙水压力状态进行分析与预测，从而确定其边坡稳定性。图5～7 所示为不同湖水位下降速率条件下特征点1～3 的孔隙水压力变化趋势。从图5～7 可以看出：各个特征点在3 种水位下降工况下孔隙水压力均表现为逐渐下降，且与水位下降时间呈线性关系。

从图5 可以看出：非饱和区特征点孔隙水压力随湖水位下降并未产生明显变化，在水位下降8 d 过程中，以水位下降速度0.50 m/d 的水位下降工况引起孔隙水压力下降2 kPa 左右。由图6 可知：特征点2 的孔隙水压力总体仍然呈现下降趋势，且在3 种水位下降速率条件下的孔隙水压力降幅为8～15 kPa。图7 所示的特征点3 孔隙水压力与特征点1 和2 的孔隙水压力变化趋势相同，仍然是在水位下降速率为0.50 m/d工况下的孔隙水压力下降幅度最大，最大值达到40 kPa。

图5 特征点1 处孔隙水压力变化趋势Fig.5 Pore water pressure trends on feature point 1

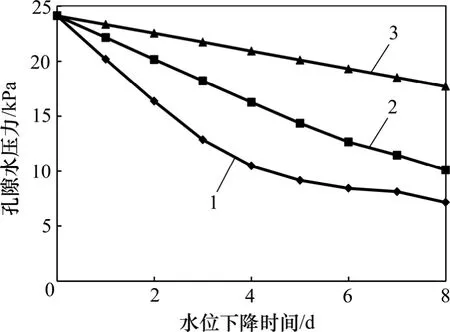
图6 特征点2 处孔隙水压力变化趋势Fig.6 Pore water pressure trends on feature point 2

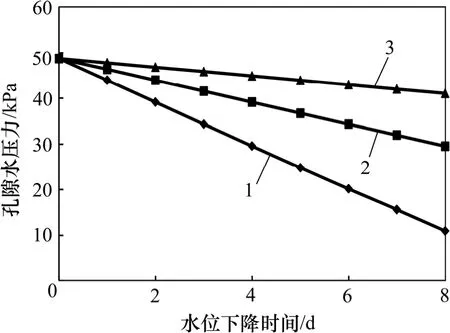
图7 特征点3 处孔隙水压力变化趋势Fig.7 Pore water pressure trends on feature point 3

对比图5～7 可知：在相同水位降低速率下，特征点1，2 和3 处土体的孔隙水压力降低幅度由大至小分别为特征点3、特征点2 和特征点1。对于同一特征点3 种水位下降速率对孔隙水压力影响程度由大至小为0.50 m/d，0.25 m/d 和0.10 m/d。由此可见：在相同计算时间内，孔隙水压力受水位下降影响的程度与水位下降速率和特征点位置密切相关，这也从另一个角度证明了水位降低幅度决定路堤内部孔隙水压力的变化特征。

3 路堤边坡稳定性分析

综合前述3 种水位变化条件以及坡率1.0:1.5 和1.0:2.0，设置高4 m、宽4 m 的护坡道3 种边坡形式，采用非饱和极限平衡法进行边坡稳定性计算，得到9组不同状态下边坡稳定性变化规律，如图8～10 所示。图11 所示为不同水位下降速率与不同路堤填筑形式下的边坡稳定性系数下降幅度与水位下降时间的关系。

由图11 可知：当水位保持不变时(初始状态下)，3 种路堤的稳定性系数分别为1.39，1.51 和1.55，均达到规范[17]中大于等于1.30 的要求；在不同的水位下降速率下，3 种路堤填筑形式稳定性系数均表现为逐渐降低的变化特征，且在同一时刻、同一水位下降速率下，设置护坡的路堤形式稳定性系数最大，坡率为1.0:1.5 的路堤形式稳定性系数最小；此外，水位下降速率为0.50 m/d 时的边坡稳定性系数下降速率较0.25 m/d和0.10 m/d的下降速率对边坡稳定性的影响要大，表现为在同一时刻、同一路堤填筑形式下，水位下降速率快的稳定性系数更低。由图11 可知：在相同水位下降速度状态下，不同填筑形式的路堤稳定性系数下降幅度差异较小；同时，水位下降速率越快，边坡稳定性系数下降越快，在水位下降速度为0.50 m/d 状态下的稳定性系数下降幅度约为0.10 m/d 时的3 倍，表明湖水位下降速率对沿湖路堤边坡稳定性产生极大影响。

路堤稳定性系数在不同水位下降速率与不同填筑形式下出现上述规律的原因可概括为以下3 点：1) 在水位下降过程中，虽然部分土体排水后基质吸力有所增加，土体的抗剪强度提高，在一定程度上可以提高边坡稳定性，但由于路堤填土压实度较高，孔隙率较低，内外水位变化速率差异较大，导致路堤内外出现一定的水位差，从而使部分区域产生超孔隙水压力，减少作用在土体上的有效应力，不利于边坡稳定；2) 在水位下降过程中，湖水对边坡的浮力迅速下降，而土体中的孔隙水由于土体渗透系数迅速下降而不能及时排出，在失去外部浮力的同时，内部土体重度保持不变，导致路堤边坡稳定性下降；3) 水位降低后，由于孔隙水并未及时排出，土体在短时间内仍然表现为饱和状态，基质吸力所提供的土体抗剪强度增大值远小于下滑力的增加值，从而引起各种水位下降速率情况下稳定性系数均逐渐减小。

图8 水位下降速度为0.50 m/d 时稳定性系数与时间的关系Fig.8 Relationship between stability factor and time when drawdown rate is 0.50 m/d

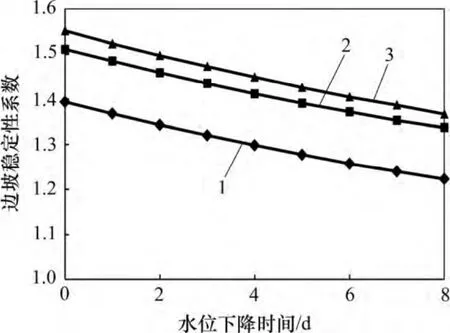
图9 水位下降速度为0.25 m/d 时稳定性系数与时间的关系Fig.9 Relationship between stability factor and time when drawdown rate is 0.25 m/d

图10 水位下降速度为0.10 m/d 时稳定性系数与时间的关系Fig.10 Relationship between stability factor and time when drawdown rate is 0.10 m/d

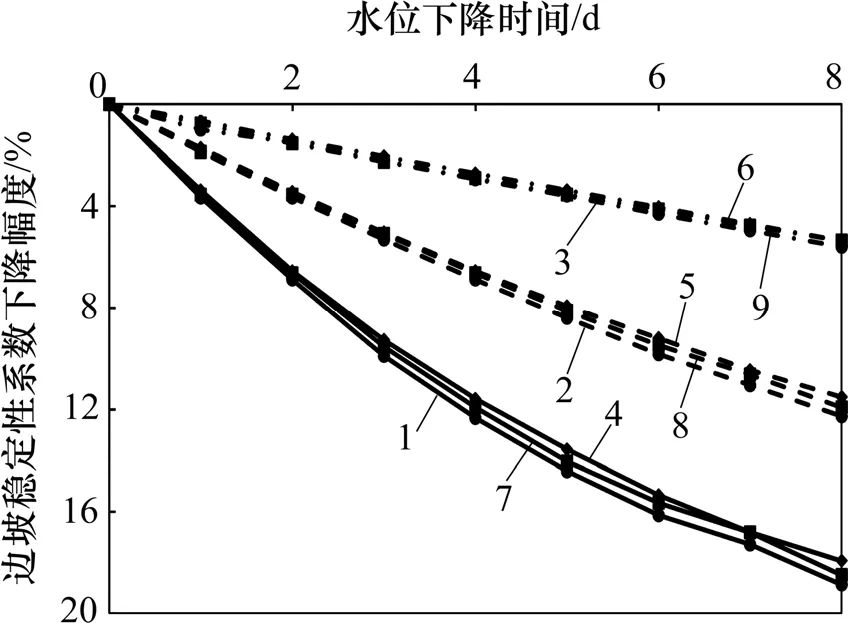
图11 稳定性系数下降幅度与时间的关系Fig.11 Relationship between decrease ratio of stability factor and time

4 结论

1) 水位下降将引起沿湖路堤内部孔隙水压力降低，路堤边坡坡脚处孔隙水下降幅度相对坡面更为显著，路堤内部孔隙水压力分布随水位下降的改变无明显变化；在相同时间内，水位下降速率越快，路堤内部孔隙水压力下降越明显。

2) 在不同水位下降速率下，路堤边坡稳定性系数都表现为持续降低，在相同时间内，水位下降越快，稳定性系数降低幅度越大；不同的路堤填筑形式对水位下降条件下的稳定性系数变化有一定程度的影响，但变化趋势仍然一致。

3) 水位下降条件下的路堤渗流特征与稳定性受水位下降速率与路堤填筑形式的共同影响，主要表现为路堤内部不同位置孔隙水压力下降幅度差异较大，使部分土体产生超孔隙水压力、外部水体推力消失和基质吸力恢复缓慢。

[1] 刘炜. 循环经济与环洞庭湖经济圈可持续发展战略[J]. 国土与自然资源研究, 2006(3): 23-24.LIU Wei. Cycle economy and sustainable development strategies in Pan-Dongting Lake economic circle[J]. Territory & Natural Resources Study, 2006(3): 23-24.

[2] 江冰. 环鄱阳湖经济圈形成与发展实证研究[D]. 北京: 中国政法大学研究生院, 2008: 16-18.JIANG Bing. An empirical study of the formation and development of Poyang lake economic circle[D]. Beijing: China University of Political Science & Law. Graduate School, 2008:16-18.

[3] 张玉, 徐卫亚, 邹丽芳, 等. 降雨条件下大型滑坡体渗流稳定性分析[J]. 岩土力学, 2013, 34(3): 833-841.ZHANG Yu, XU Weiya, ZOU Lifang, et al. Analysis of seepage stability of large-scale landslide under rainfall condition[J]. Rock and Soil Mechanics, 2013, 34(3): 833-841.

[4] 杨帆, 张发民, 王文远, 等. 考虑库水位变动影响的岸坡稳定性分析[J]. 科学技术与工程, 2013, 13(5): 1383-1387.YANG Fan, ZHANG Famin, WANG Wenyuan, et al. Bank slope stability analysis on considering reservoir water level fluctuation[J]. Science Technology and Engineering, 2013, 13(5):1383-1387.

[5] 张在忠. 湖区高填方路基吹砂填筑施工技术[J]. 企业技术开发, 2006, 25(6): 36-37.ZHANG Zaizhong. Filling technology of blowing sand for high embankment in lake area[J]. Technological Development of Enterprise, 2006, 25(6): 36-37.

[6] 廖红建, 盛谦, 高石夯, 等. 库水位下降对滑坡体稳定性的影响[J]. 岩石力学与工程学报, 2005, 24(19): 3454-3458.LIAO Hongjian, SHEN Qian, GAO Shihang, et al. Influence of drawdown of reservoir water level on landside stability[J].Chinese Journal of Rock Mechanics and Engineering, 2005,24(19): 3454-3458.

[7] 刘东燕, 侯龙, 郑志明. 水位变动对库区边坡稳定性的影响机理研究[J]. 地球与环境, 2012, 40(1): 70-75.LIU Dongyan, HOU Long, ZHENG Zhiming. Research on the stability of reservoir slope and the corresponding influence mechanisms induced by fluctuation of water level[J]. Earth and Environment, 2012, 40(1): 70-75.

[8] 王思长. 库岸公路碎裂岩质高边坡稳定性研究[D]. 西安: 长安大学公路学院, 2011: 118-119.WANG Sichang. Stability study on cataclastic rock high slope of reservoir banks highway[D]. Xi’an: Chang’an University.Highway Institute, 2011: 118-119.

[9] 尚义敏, 彭斌, 梅涛, 等. 地下水位变化对边坡稳定性影响的模拟分析[J]. 环境科学与技术, 2013, 36(S1): 366-369.SHANG Yimin, PENG Bin, MEI Tao, et al .Numerical analysis on the stability of a slope behind a substation under varying of ground water level[J]. Environmental Science & Technology,2013, 36(S1): 366-369.

[10] 毛昶熙. 渗流计算分析与控制[M]. 北京: 中国水利水电出版社, 2003(9): 56-63.MAO Changxi. Seepage computation analysis & control[M].Beijing: China Water Power Press, 2003(9): 56-63.

[11] van Genuchten M T H. Closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Sci Soc Am,1980, 44: 892-898.

[12] Ho D Y F, Frellund D G. A multistage triaxial tests for unsaturated soils[J]. ASTM Geotechnical Testing Journal, 1982,5(1/2): 18-25.

[13] John K. Geo-slope International Ltd. Stability modeling with slope/W2007 version[R]. Calgary, Canada: Geo-slope International Ltd, 2008: 315-331.

[14] Frellund D G, Rahardjo H. 非饱和土力学[M]. 北京: 中国建筑工业出版社, 1997: 46-50.Frellund D G, Rahardjo H. Soil mechanies for unsaturated soil[M]. Beijing: China Building Industry Press, 1997: 46-50.

[15] 侯龙. 非饱和土孔隙水作用机理及其在边坡稳定分析中的应用研究[D]. 重庆: 重庆大学土木工程学院, 2012: 95-102.HOU Long. Research on the mechanism of pore water action within unsaturated soil and the corresponding slope stability[D].Chongqing: Chongqing University. School of Civil Engineering,2012: 95-102.

[16] 柳群义, 朱自强, 何现启, 等. 水位涨落对库岸滑坡孔隙水压力影响的非饱和渗流分析[J]. 岩土力学, 2008, 29(增刊):85-89.LIU Qunyi, ZU Ziqiang, HE Xianqi, et al. Unsaturated seepage analysis of the influence of water level fluctuation on pore water pressure of landslide in reservoir area[J]. Rock and Soil Mechanics, 2008, 29(Suppl): 85-89.

[17] JTG D30—2004, 公路路基设计规范[S].JTG D30 — 2004, Specifications for design of highway subgrades[S].