偶氮二甲酰胺发泡剂清洁生产评价模型

赵建喜，赵丽娜，史 翎

（1.北京化工大学 理学院，北京 100029；2. 北京化工大学 材料科学与工程学院，北京 100029）

偶氮二甲酰胺（ADC）发泡剂是最重要的肼基发泡剂［1］。在我国，ADC发泡剂的生产工艺主要为尿素法，少数外资或合资企业采用酮联氮法。尿素法生产工艺会产生大量的污染物，氨氮废水的排放量超过10 Mt/a［2］。

目前，针对ADC发泡剂清洁生产评价方面的研究较少。在构建评价指标体系方面，主要有李文军［2］的定量体系和朱宝菊等［3］的综合体系。在确定评价指标权重方面，常用方法包括专家咨询法［2］、层次分析法［3-6］和模糊综合评价法［7-8］等。对于评价指标的单向评价指数，常采用比值法确定［2-3］；对于综合评价指数，则采用加权求和法确定［2-3］。这几种方法简单直观，但存在主观性强、指标间信息交叉、线性效果差、需要寻找或求基准值等缺点。

本工作提出了基于逐层序关系分析法、极差标准化法、主成分分析法的ADC发泡剂清洁生产评价模型，有效克服了原模型的诸多不足。

1 理论与方法

1.1 基于尿素法和酮联氮法的评价指标体系

朱宝菊等［3］的定量与定性评价指标体系较为完善地覆盖了尿素法ADC发泡剂清洁生产工艺的各个方面，虽然其定性部分主观性过于强烈且相关资料不易获取，可操作性不强，但其定量部分可从一定程度上反映出定性体系的部分内容。因此，采用朱宝菊等的定量评价指标体系。

该定量评价指标体系包括目标层（A层）、准则层（B层）和方案层（C层）。目标层（A层）包括资源与能源消耗指标（A1）、产品特征指标（A2）、污染物产生指标（A3）、资源综合利用指标（A4）和环境管理与劳动安全卫生指标（A5）。准则层（B层）包括能量消耗指标（B1）、原料消耗指标（B2）、新鲜水消耗指标（B3）、产品优级品率（B4）、产品特征（B5）、产品改性比例（B6）、废水（B7）、废气（B8）、废渣（B9）、盐酸综合利用率（B10）、含氨废水综合利用率（B11）、硫酸钙综合利用率（B12）、十水碳酸钠综合利用率（B13）、职业病发生率（B14）、年投入环保资金（B15）、伤亡事故率（B16）和劳保投入额（B17）。方案层（C层）包括尿素消耗（C1）、硫酸消耗（C2）、烧碱消耗（C3）、氯气消耗（C4）、产品发气量（C5）、产品分解温度（C6）、产品含水量（C7）、废水量（C8）、COD（C9）、废水中氨氮含量（C10）、废水中盐总量（C11）、废气量（C12）、废气中氯化氢含量（C13）和废渣（十水碳酸钠+硫酸钙干基）量（C14）。

针对酮联氮法的评价指标体系与针对尿素法的评价指标体系基本相同，不同之处在于尿素法生产过程需要原料硫酸，而酮联氮法需要氨和丙酮（丙酮实际并未消耗）。为综合评价不同工艺的产品生产企业，假定硫酸在尿素法评价指标体系中的重要性与氨和丙酮在酮联氮法评价指标体系中的重要性相同。

1.2 逐层序关系分析法

确定目标层A1，A2，A3，A4，A5的序关系（指标重要性的排序）［9］。

参考（10/10）～（18/2）标度［10］，给出序关系下相邻两指标的权重（ω）的比值（r）。

计算各定量评价指标的影响因子，计算结果见表1。

表1 各定量评价指标的影响因子

1.3 极差标准化法

清洁生产评价指标体系分为正向指标和逆向指标两部分。对于正向指标，数值越大越符合清洁生产的要求；对于逆向指标，数值越小越符合清洁生产的要求［2］。极差标准化法［11］有正线性相关式和负线性相关式两种表达形式，分别见式（6）和式（7）。极差标准化法符合正向指标与逆向指标的要求，且在实际应用中的线性效果较好。

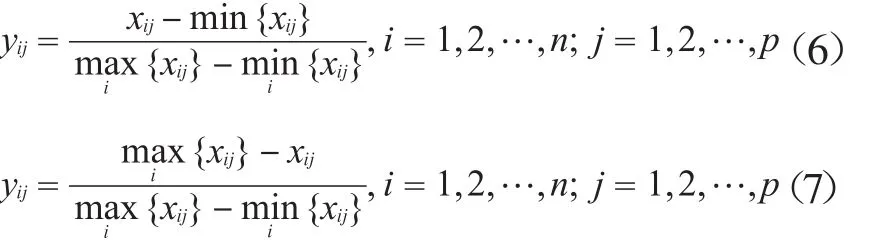
式中：xij表示第j个指标、第i个试样的原指标值；yij表示xij经极差标准化后的数值；n为试样的个数；p为指标的个数。

极差标准化法消除了各评价指标数据量纲和数量级的影响。但各指标数据不具备同趋性，即重要性水平不同。所以，将各评价指标数据乘以对应的影响因子，从而使其具备可比性。

1.4 主成分分析法

主成分分析法是指将具有一定相关关系的指标重新组合成一组新的少数相互无关的综合指标的统计方法［12］。在实际应用中，几个最大的主成分所包含信息的总和即代表了大部分的原有信息。该方法避免了指标间的相关性对分析结果造成影响，克服了加权求和法信息重叠的缺陷。

2 实例分析

本工作选取7家尿素法ADC发泡剂生产企业（分别为江苏某公司、福建某公司1、福建某公司2、江西某公司、湖南某公司、广东某公司和山东某公司2）和1家酮联氮法ADC发泡剂生产企业（山东某公司1），并获得了各项清洁生产评价指标数据。对于正向指标，用式（6）标准化；对于逆向指标，用式（7）标准化。通过式（6）与式（7）将原指标值变换到［0，1］区间，以消除量纲和数量级影响。将经过极差标准化法处理后的各评价指标数值乘以对应的影响因子，使各指标数据具备同趋性，然后进行主成分分析。

由于极差标准化属于标准化的一种，故可略过主成分分析中原有的z-score标准化过程，直接用MATLAB数学软件编程，进行后续计算。主成分分析的计算过程如下。

1）建立试样协方差矩阵S。

2）求试样协方差矩阵S的特征值及相应的单位特征向量。

3）选择主要的主成分：经计算，前两个主成分的方差累计贡献率大于85%，说明前两个主成分基本包含了原指标所具有的信息，因此仅提取前两个主成分即可。

4）构造综合评价指标（F）。

式中：F1为提取的第一主成分的评价指标，F2为提取的第二主成分的评价指标。根据前两个特征值对应的特征向量组成的矩阵，可找出每个主成分对应的有较大影响力的原指标。第一主成分对应的有较大影响力的指标为尿素消耗量、硫酸消耗量、烧碱消耗量、氯气消耗量、新鲜水消耗量、废水量、COD和废水中氨氮含量，各指标对主成分的影响值［12］分别为0.403 0，0.161 7，0.317 5，0.262 9，0.205 8，0.232 3，0.424 6，0.539 6。前5个指标为资源消耗，后3个指标为主要污染物，所以第一主成分可命名为资源消耗与废水污染物产生指标；第二主成分对应的有较大影响力的指标为含氨废水综合利用率（指标对主成分的影响值为0.705 1），其影响值远大于其他指标的影响值，故将第二主成分命名为含氨废水综合利用率指标。

3 结果与讨论

3.1 主成分分析法的计算结果

根据综合评价指标计算各企业得分。企业得分越高，说明其清洁生产水平越高，反之越低。主成分分析法的计算结果见表2。

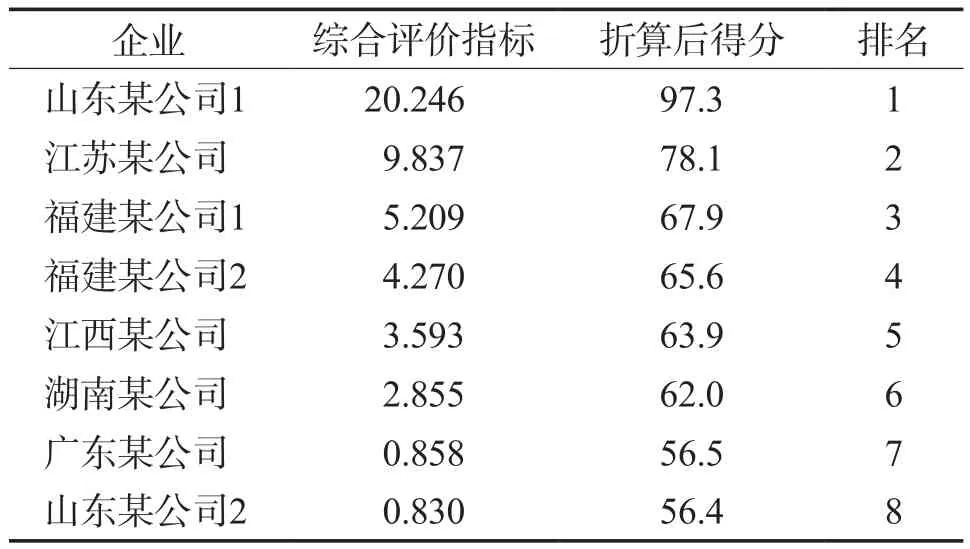
表2 主成分分析法的计算结果

按照加权求和法［2-3］计算得到的各公司的得分及排名见表3。

表3 加权求和法的计算结果

对比表2和表3可知：在主成分分析法中，福建某公司2和湖南某公司分别排名第四和第六，广东某公司和山东某公司2分别排名第七和第八；在加权求和法中，福建某公司2和湖南某公司分别排名第六和第四，广东某公司和山东某公司2分别排名第八和第七，与主成分分析法所得排名相反。这是由于，原指标间具有一定的相关性，即指标间有不同程度的信息重叠，加权求和会导致信息的重复计算，导致最终结果失真，而主成分分析法将相关指标转化为新的相互无关指标，避免了指标间的相关性对结果造成的影响。综合分析比较，主成分分析法所得结果更具可信性。

3.2 清洁生产水平等级划分和结果成因分析

将ADC发泡剂生产企业清洁生产水平划分为优秀（90.0～100（折合后得分，下同））、良好（70.0～89.9）、一般（60.0～69.9）、不合格（0～59.9）4个等级。 各企业的清洁生产等级见表4。

表4 各企业的清洁生产等级

由表4可知，在8家ADC发泡剂生产企业中，有6家清洁生产水平合格，2家不合格。山东某公司1作为唯一一家使用酮联氮法的企业，得分显著高于其他公司，清洁生产等级为优秀。酮联氮法在较大程度上避免了酸、碱的无效消耗，原料利用率提高，副产物的种类和数量减少，物料消耗显著降低；与尿素法相比，酮联氮法不需要冷冻脱盐，能量消耗低；酮联氮法的外排废水主要成分为氯化钠，污染物产生量小。

江苏某公司综合能耗和新鲜水消耗量明显小于其他6家公司，而且严格控制污染物的排放，废水中主要污染物氨氮、COD排放量小，清洁生产等级为良好。广东某公司和山东某公司2在资源消耗和污染物产生方面较差，前者的尿素、烧碱、硫酸消耗多，废水中氨氮、COD、总盐量含量极高；后者的新鲜水、尿素、烧碱和氯气消耗多，废水中氨氮、COD含量极高。

3.3 小结

逐层序关系分析法是对层次分析法的改进，该方法不用建立判断矩阵和检验一致性，计算量减少。相对于专家咨询法，逐层序关系分析法可以计算大量指标的影响因子，且计算结果精确。极差标准化法不需要寻找或计算各评价指标的基准值，克服了比值法中逆向指标公式非线性的缺陷。主成分分析法避免了指标间信息交叉对结果的影响。将以上3种方法首次应用于ADC发泡剂清洁生产评价领域，优势明显且实证效果好。

4 结论

a）提出了一套完整的针对不同生产工艺的ADC发泡剂清洁生产企业综合评价模型。该模型涉及逐层序关系分析法、极差标准化法和主成分分析法3种方法。

b）采用逐层序关系分析法可确定各评价指标的影响因子，采用极差标准化法可消除指标数据量纲和数量级影响，采用主成分分析法可对各生产企业进行排名。

c）该模型合理可行，为ADC发泡剂生产企业的清洁生产评价提供了一个参考方案。

［1］ 游贤德. ADC发泡剂生产现状与改性产品的开发［J］.江苏化工，2001，29（1）：33-35.

［2］ 李文军. ADC发泡剂企业清洁生产评价指标体系研究［D］. 北京：北京化工大学化学工程学院，2008.

［3］ 朱宝菊，史翎，江莉，等. 尿素法ADC发泡剂清洁生产评价指标体系［J］. 化工环保，2011，31（3）： 260 -264.

［4］ 陈平. 清洁生产指标评价方法［J］. 化工环保，2004，24（1）：55-57.

［5］ 巴亚东. 环境影响评价中的清洁生产分析方法［J］. 环境科学与技术，2010，33（12）：598-601.

［6］ 杨光忠. 氰化提金企业清洁生产评价体系的研究［J］.环境科学与技术，2009，32（9）：195-196.

［7］ Zou Zongxian，Wei Yang，Sun Xiaofei，et al. Risk assessment of concentrating solar power based on fuzzy comprehensive evaluation［J］. Systems Eng Pro，2012，4：99-106.

［8］ 杨亚军，孙建华. 基于模糊综合评价模型的项目风险评估［J］. 统计与决策 ，2009 （22）：62-64.

［9］ 郭亚军. 综合评价理论、方法及应用［M］. 北京：科学出版社，2007： 44-45，192-197.

［10］ 郭亚军，张发明，易平涛. 标度选择对综合评价结果的影响及合理性分析［J］. 系统工程与电子技术，2009，30（7）：1277-1280.

［11］ 殷培杰，杜世勇，白志鹏. 2008年山东省17城市生态承载力分析［J］. 环境科学学报，2011，31（9）：2048 -2057.

［12］ 于秀林，任雪松. 多元统计分析［M］. 北京：中国统计出版社，2010：154-168.