波浪对挖泥船抓斗平挖作业的影响分析＊

赵 鑫 李竹森 肖汉斌 张永涛

（武汉理工大学物流工程学院1） 武汉 430063） （营口港集团股份有限公司固机分公司2） 营口 115000）

0 引 言

目前国内正在设计研制的新型智能化大型抓斗挖泥船的抓斗平挖运动是通过对抓斗钢丝绳运动的控制来实现的，理论上的平挖精度可以控制在±25cm之内.但是，由于大型抓斗挖泥船的实际施工状况比较复杂，尤其是在进行航道疏浚和大型海洋工程建设作业的过程中，挖泥船会受到海面波浪的影响而造成挖泥船在波浪力作用下的运动，这种运动是否会对挖泥船进行平挖作业造成影响，如果有影响，影响程度如何，是否能够保证±25cm的平挖精度，本文将对以上问题进行简要分析.

船舶在波浪载荷的作用下产生复杂的运动，因此分析波浪对挖泥船抓斗的影响实际上就是分析在波浪的作用下挖泥船船体的受力及运动.由于挖泥船的定位方式不同，其在波浪力作用下的运动响应也不同，以下主要针对以定位桩方式定位的挖泥船进行分析.

1 船舶摇荡运动分析

挖泥船在海上进行工作时，分析波浪对挖泥船的影响和分析波浪对普通船舶的影响最大的不同之处在于挖泥船由于定位桩或定位锚的作用而停留在海面某一固定位置进行作业，从而不用考虑船舶航速引起的耦合作用.在波浪的作用下船舶将产生6个自由度方向的运动（见图1），包括沿X轴方向的纵荡（行驶）运动和绕X轴方向的横摇（横倾）运动，沿Y轴方向的横荡（横移）运动和绕Y轴方向的纵摇（纵倾）运动，以及沿Z轴方向的垂荡（沉浮）运动和绕Z轴方向的首摇（回转）运动.

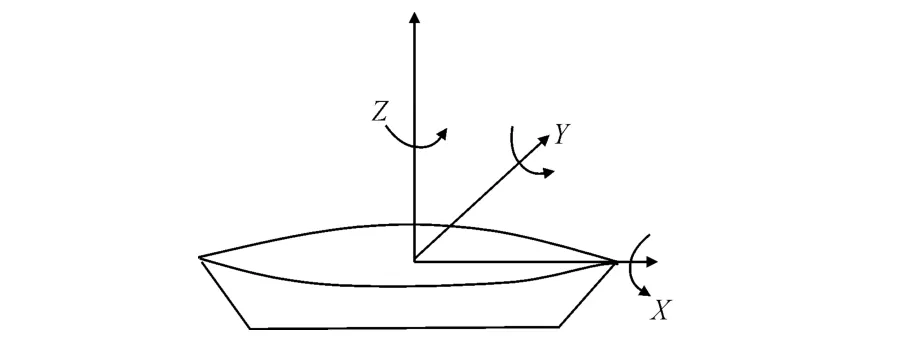
图1 船舶6自由度方向运动

对于有多个定位桩进行定位的挖泥船而言，其横荡和首摇运动被限制住；另外，挖泥船可以看成是一个左右对称的细长船体，其纵荡运动的数量级相比于其他自由度方向的运动的数量级而言较小，可以不予考虑；对于横摇运动，横摇对挖泥船抓斗定位的影响可以归结为船倾一类（此类将单独分析）；采用定位桩方式定位的挖泥船，由于定位桩特有的卡箍式结构［1］，当挖泥船在海面作业时，定位桩一端插入泥沙中，另一端套有2个有一定间隔的卡箍和挖泥船船尾相连.因此，整个定位桩系统限制了船舶的纵摇，使船体只能做沿着定位桩竖直方向的垂荡运动和绕桩腿的首摇运动，所以纵摇也可不予考虑.综上，针对以定位桩方式进行定位的挖泥船主要考虑船体在波浪中的垂荡运动.

2 船舶运动方程的建立

对于船舶摇荡运动的分析往往要考虑多方面的因素，比如船的航速、航向角等，因此为了便于分析而又不影响结果的准确性，通常在研究船舶摇荡时，作如下假设［2］：（1）船体为刚体，即忽略弹性变形的影响；（2）作用于船体上的波浪是深水微幅波，从而忽略浅水波和高阶非线性波浪的影响.

以上2个假定经常被用于分析船舶在波浪中的运动，基于此假定得到的分析结果同实验结果相比也有较高的可信度.

在迎浪零航速情况下，船体垂荡运动是基于切片理论进行分析的［3］，切片理论认为，船舶在做摇荡运动过程中，其周围的流体只发生沿船舶横剖面方向的流动.因此，将船舶沿船长方向横剖为若干切面，对每一切面进行受力分析，从而将涉及船体的三维空间问题转化为平面问题.

用牛顿第二定律可以写出船舶迎浪航行时的对称运动方程［4］为

式中：Q为船舶质量；z为船舶重心O1处的垂荡位移；F为流体对船舶总的作用力.由切片理论的知识可知，F由流体静力F1、附加惯性力F2和兴波阻尼力F3组成，但不是简单的求其代数和，而是首先求得船舶任一横剖面上3种力的代数和，然后将其沿整个船长方向进行积分求和，所得的力即为流体对船舶的总作用力.用公式表示为

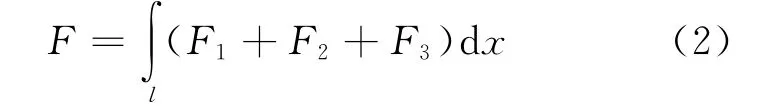
现将3个力分别分析，如图2所示.

1）流体静力 此处的流体静力又叫恢复力，其本质是船舶位于水面的浮力，由切片吃水变化引起.船体位于波面的位移用公式wr＝z－θxζ＊表示.其中：θ为船舶的纵摇角；ζ＊为考虑了史密斯修正后的波面升高.通过以上对定位桩的分析船舶的纵摇角为零，因此位移简化为wr＝zζ＊.由浮力公式即可推导出此处流体静力的表达式为

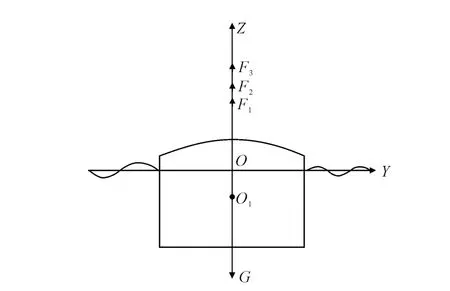
图2 船体任意剖面上的受力

式中：yw（x）为x处的水线半宽；ρ为水的密度；g为重力加速度.

2）附加惯性力 此处的附加惯性力即是单位切片上附加质量产生的动量的变化率.计算公式为

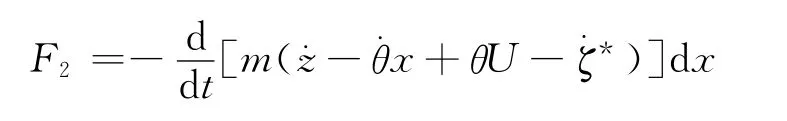
由以上对挖泥船进行的摇荡运动分析可知，用定位桩定位的抓斗挖泥船在海面进行清淤工作时，其纵摇角和航速均为零，即θ＝0，U ＝0.则F2可以简化为式中：m为单位切面的附加质量；U为船舶航速；θ为航向角.

3）兴波阻尼力

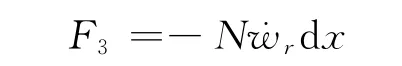
因为 ζ＝x＋Ut，

由上面对沿船长方向进行积分得到的总的流体作用力的表达式（2），代入运动方程式（1）并化简得到船舶垂荡运动的表达形式如下.

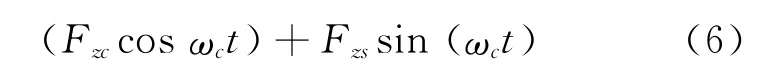
式中：φ为纵摇角；ωc为遭遇周期.本文中纵摇角为零，即φ＝0，由于分析的是船舶零航速的情况，所以遭遇周期ωc即为波浪周期ω，即ωc＝ω.因此，以上垂荡运动方程可以简化为：

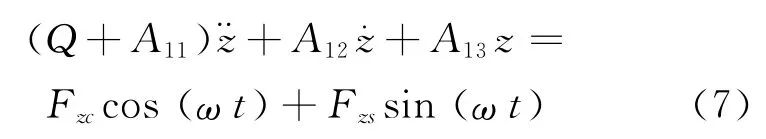
由式（7）可见，船在水面做垂荡运动的模型视为单自由度有阻尼系统的振动，垂荡运动的微分方程的一般形式为

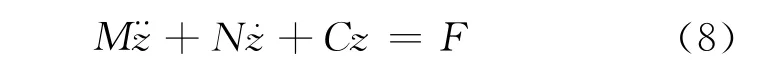
式中：M为垂荡运动惯性力系数；N为垂荡运动阻尼力系数；C为垂荡运动恢复力系数；F为垂荡运动流体对船舶的总作用力.

式（7）左边系数

和分析船舶垂荡运动一样，船舶航速为零时，遭遇周期即为波浪周期，即U＝0，T＊＝T.

则方程右边的波浪干扰力

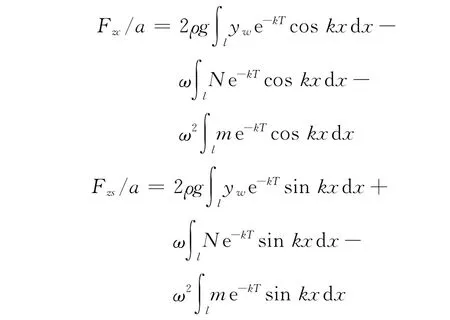
式中：a为波幅，a＝H／2，H 为波高；ρ为海水密度；k为波数，k＝2π／λ；T 为船舶吃水；ω 为波动圆频率，ω＝2π／T.

将以上算得的各项参数代入式（7）进行化简，用比较系数法列出方程组，最后通过MATLAB编程求解即可求得在深水微幅波下垂荡运动的位移z（t），z（t）的通式可以写为

式中：za为垂荡运动的振幅；ωc为遭遇频率；εz为垂荡与波浪的相位差.

对于水动力系数（附加质量和阻尼系数）的求解运用保角变换［5］的方法即可求得.因为对于大型抓斗挖泥船而言，其剖面为一般船型剖面，而非复杂船型剖面，属于最简单的保角变换方法的求解范畴，所以只需通过船体剖面的半宽、水下面积、吃水深度即可求得船体剖面的水动力系数［6］.

3 影响结果分析

由式（9）可见，船舶在波浪作用下船体的垂荡运动主要与遭遇频率ωc有关，由于挖泥船施工过程中航速为零，所以遭遇频率即为波浪频率，因此特定挖泥船船体由波浪引起的升沉运动主要和波浪频率有关.以某大型抓斗挖泥船为例：挖泥船船长63.5m，型宽14.5m，型深5.0m，设计吃水3.5m.选取波浪频率为0.5 L（L为船长）波长所对应的频率，经计算ω值为1.39rad／s.通过保角变换的方法求得水动力系数后，再通过 MATLAB编程可得式（7）中各项系数 A11，A12，A13，Fzc以及Fzs的值，代入式（7）并整理即可得船舶垂荡运动方程，其结果为：z（t）＝0.016 7cos（ωt－0.56），m.由此式可以看出，当选取波长为0.5 L所对应的频率时，波浪引起船舶垂荡位移最大为1.67cm.同理，当选取波浪频率为1.25 L波长所对应的频率时，得到船舶垂荡最大位移为35.9cm，超出了±25cm的平挖精度，已经对平挖造成了很大的影响.选取多个频率数值，经计算绘制出垂荡运动幅频响应曲线，而为了方便比较与观察垂荡运动幅值，用其无因次形式表示，见图3.

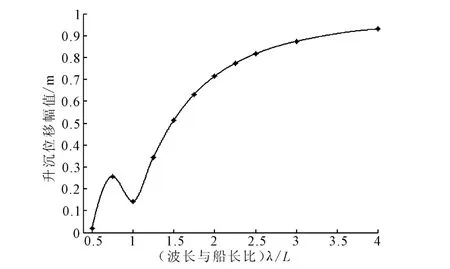
图3 各频率下升沉运动幅值

从图3中可以看出，随着波浪频率的增大，船舶垂荡位移也相应减小，而当频率为0.75 L波长的波浪所对应的频率时，船舶垂荡位移发生突变是因为在此频率时波浪扰动力或力矩的频率等于垂荡运动的固有频率而发生谐振.对应于实际情况中，考虑到挖泥船的实际施工状况，尤其是对于船长超过50m的大型抓斗挖泥船在内河或者湖面进行清淤工作时，挖泥船所遇到的波浪波长很少有超过0.5 L的情况，也即波浪频率远大于1.39rad／s，因此对应于图3可以看出由波浪引起的船舶垂荡位移也就远小于1.67cm.因此，从此例看，大型抓斗挖泥船船体垂荡引起的位移相对于±25cm的平挖精度可以忽略不计.其他类型挖泥船依然可以用此方法从理论上计算其垂荡位移，可以得出类似结果.

以上只是对挖泥船在多数正常工作条件下的分析结果，从结果中可以看出，针对于大型抓斗挖泥船在内河或者湖面进行清淤工作时，波浪对于挖泥船平挖的影响可以忽略.当然，如果大型抓斗挖泥船处于极端工作条件下，比如挖泥船在进行海洋工程建设而工作于海上且蒲氏风力等级达到5级的劲风情况时，此时风浪引起挖泥船垂荡位移将超过±25cm的精度，对于这种情况，由于挖泥船垂荡运动的位移—时间函数是余弦函数，其引起的抓斗升沉运动将很难从控制钢丝绳的角度进行补偿，寻求一个有效地补偿方法也很困难，所以若想保证挖泥船平挖过程不受到波浪的影响，就应当尽量避免挖泥船在这种极端的工况条件下进行作业.

［1］付丽丽.挖泥船定位桩系统在波浪载荷下的疲劳强度分析［D］.天津：天津大学，2009.

［2］张建.船舶在波浪中的纵向运动响应及载荷［D］.大连：大连理工大学，2005.

［3］戴仰山，沈进威，宋竞正.船舶波浪载荷［M］.北京：国防工业出版社，1996.

［4］董艳秋.船舶波浪外荷和水弹性［M］.天津：天津大学出版社，1991.

［5］刘应中，廖国平.船舶在波浪上的运动理论［M］.上海：上海交通大学出版社，1987.

［6］王学亮.大型起重船在海浪中的运动响应研究［D］.天津：天津大学，2003.