转体施工桥梁大吨位球铰径向应力计算方法优化研究＊

车晓军 周庆华 关林坤

（武汉理工大学交通学院 武汉 430063）

0 引 言

转体施工的关键构件是承载整个转体重量的转动球铰，为做到球铰设计与施工的合理可靠，不仅需要丰富的现场经验，更需从揭示球铰的受力规律出发，提出相应的理论计算方法.

然而，目前设计人员广泛采用简化计算方法［1］，即把球铰接触面简化为平面，从而进行球铰接触面的正应力计算，同时通过面域内的积分求得启动力矩和转动力矩［2－3］.然而，实际上球铰接触面应为曲面，应力分布比较复杂.

从球铰的真实受力状态出发，分析球铰接触面的压应力分布，对目前规范中采用的简化计算方法进行优化，并结合工程实例进行对比分析，丰富和完善球铰设计理论和方法.

1 球铰受力状态及简化算法

1.1 球铰受力状态分析

在求解球铰接触面正应力之前，需先了解球铰接触面的受力状态.如图1所示，球铰结构接触面上任意一点所受的力都可以分解为3项：径向力Nr、经过球心的竖平面内与球面相切方向的力NV、经过球心的水平面内与球面相切方向的力.

由球铰的受力状态可知，Nv和Nh为接触面的摩擦力，只有在接触面之间有相对错动的趋势时才会产生.其数值也与径向力Nr及摩擦系数有关，然而在转体前球铰承受对称的恒载作用（即无偏心作用），此时上下球铰保持相对静止，因此不存在摩擦力，而只有径向力 Nr作用［7－9］.

图1 球铰接触面受力图示（无偏心作用）

1.2 球铰径向应力的简化算法

现行规范中采用将球铰接触面简化成平面接触的计算方法，因此，竖向正应力公式为

式中：F为下承台集中力大小；R1为球铰的支撑半径.

简化算法虽然计算方便，但对实际结构受力状态进行很大程度的简化，主要体现在：（1）球铰构造的简化 将球铰接触面简化为平面接触，而实际上球铰接触面为曲面，应力分布较平面要复杂；（2）球铰荷载的简化 简化算法假设球铰在对称的恒载作用下，此时球铰不存在偏心，上下球铰保持相对静止，然而实际上由于制造误差及混凝土的质量分布差异、预应力钢束的张拉差异等影响，球铰施工不可避免存在一定的误差，即使进行了称重配重之后也会承受一定程度的偏心作用.

2 球铰径向应力计算的优化算法

2.1 球铰径向应力受力状态图示

由弹性力学知识可知，半平面体在边界上作用集中力时，径向应力的表达式为

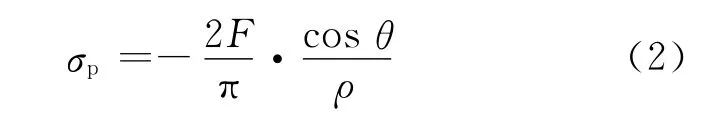
式中：σp为径向应力；F为集中力大小；θ为球面上某点的径向角度；ρ为球的半径.

由式（2）可知，半平面体在边界上作用集中力时，径向应力与cosθ成正比，那么对于球铰结构的受力状态，可以参考类似的解答，受力图示见图2.

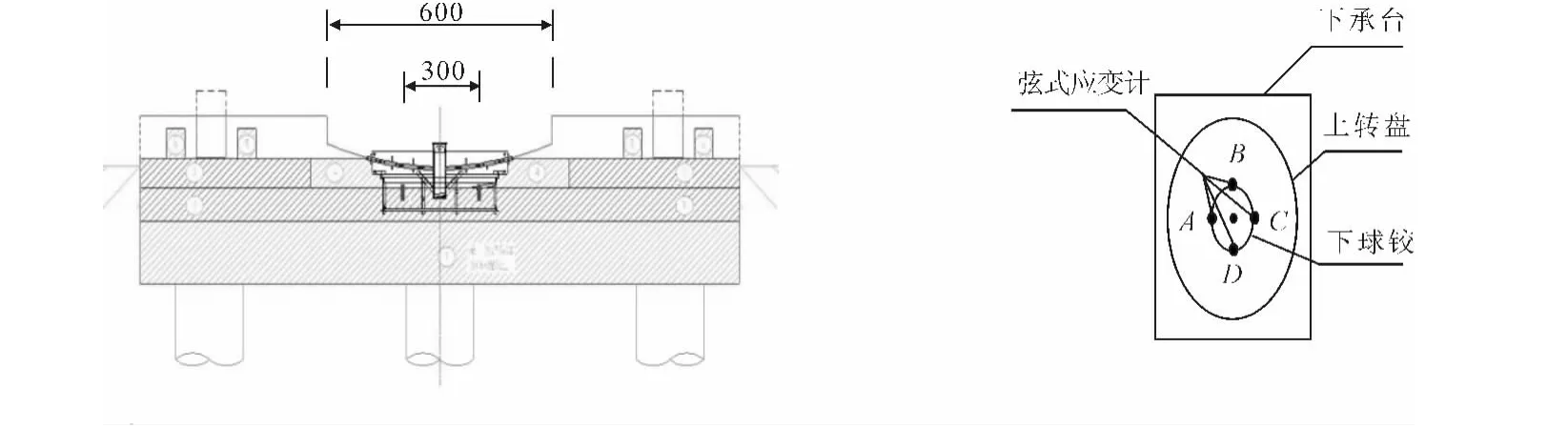
图3 下球铰应力传感器布置图

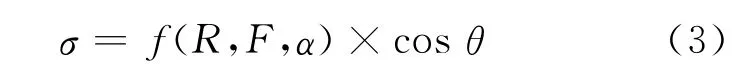
式中：σ为球铰的径向应力；R为球铰的半径；R1为球铰支承半径；α球面上某点的圆心角.

3 对比分析

3.1 工程概况

跨京包线铁路2×75m单T变截面连续箱梁桥，因考虑减小对铁路运营的影响，桥梁采用先平行铁路搭设支架现浇后平面转体法施工，其中转体段长度为69m，球铰采用钢制球铰，其中取F＝120MN，球铰的球心半径为R＝7.7m，球铰的支撑半径为R1＝2m，分别计算简化算法与优化算法的应力分布，得到不同位置处的应力数值，并根据实测数据进行对比分析.

3.2 应力数据对比分析

将简化算法、优化算法及实测传感器的应力数据进行对比分析，见表1.

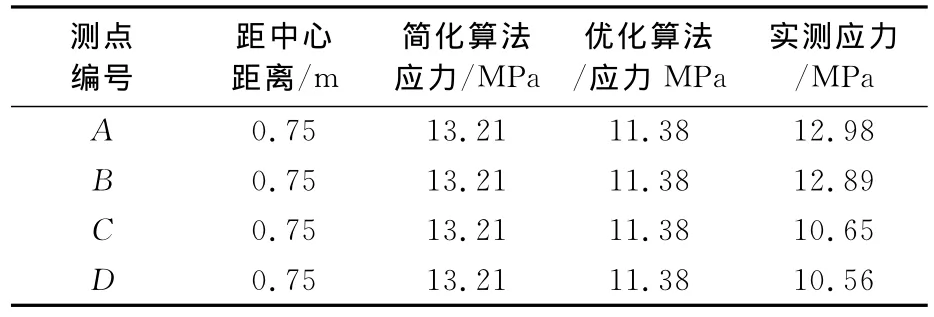
表1 球铰径向应力对比分析表测点

通过对比分析，发现对于同一测点，简化算法的计算结果较优化算法偏大接近10%，说明简化算法结果偏于保守；而实测应力中A，B2点较优化算法偏大，而C，D2点应力较优化算法偏小，证明球铰存在有AB方向一定程度的偏心.

4 结 论

1）经对比分析简化算法和优化算法应力数值，发现对于大吨位的球铰受力计算，简化算法的计算结果偏于保守，将会造成球铰的设计尺寸偏大及启动力矩富裕过多的现象.相比较而言优化算法相对更为合理，据此进行的球铰的构造尺寸设计及牵引力矩的计算也将更为准确，同时，研究还发现桥梁随着转体吨位增大，简化算法的偏差也将越大.

2）通过与实测数据对比分析，发现球铰在转体前不可避免地存在一定程度的偏心，为此在根据优化算法进行计算时，需要考虑偏心影响在应力结果上考虑增大系数的影响，保证球铰计算的安全可靠.

3）对于转体过程中的球铰受力状态分析，需考虑球铰间摩擦的影响，根据监测数据进一步完善球铰的受力分析.

［1］张联燕.桥梁转体施工［M］.北京：人民交通出版社，2001.

［2］徐芝纶.弹性力学［M］.北京：人民教育出版社，1978.

［3］徐升桥，陈国立.北京市五环路曲线斜拉桥转体施工设计［J］.铁道标准设计，2003（10）：1－5.

［4］薛 军，任文祥.T形刚构大纵坡弯斜箱梁桥水平转体施工技术［J］.铁道标准设计，2005（8）：33－37.

［5］李 跃，任伟东.大跨度连续刚构拱桥关键部位应力分析与试验［J］.铁道科学与工程学报，2007（8）：23－27.

［6］姚国文，陈生华，周志祥.竖转施工刚构拱桥转动铰接触应力有限元分析［J］.重庆建筑大学学报，2008（6）：59－62.

［7］王立中.转体施工的公路T型刚构桥梁转动结构设计［J］.铁道工程学报，2006（12）：41－43.

［8］钱桂枫，程飞等.沪杭高铁超大吨位转体施工拱桥建造技术［M］.北京：中国铁道出版社，2012.

［9］李民伟，宁晓骏.不等高双肢薄壁墩对大跨连续刚构静力影响［J］.武汉理工大学学报：交通科学与工程版，2012，36（6）：1279－1282.