上市港口企业投入产出效率研究

丁 涛 徐湘文

（武汉理工大学交通学院 武汉 430063）

0 引 言

港口业作为一个与国民经济相关产业发展联动性极强的产业，已成为了促进经济发展的“加速器”与新的经济增长点.在促进国家产业结构调整、转变经济发展方式和增强国民经济竞争力等方面港口作为“经济增长极”发挥着越来越重要的作用.随着我国经济发展方式转变、经济结构战略性调整步伐的加快，在提高效益和效率的基础上实现总量的平稳较快发展，已成为港口业健康发展的必然要求.因此，科学评价港口的投入产出效率无疑对港口企业调整发展战略、提高运营绩效有重要意义.

1 研究方法概述

目前，效率评价使用的方法主要有模糊综合评价法、层次分析法、随机前沿分析法等［1－3］.这些方法一方面主观性较强，另一方面只能从投入或产出的单一角度进行评价，以随即前沿分析（stochasticfrontieranalysis，SFA）法为例，对于多产出的情况，只能分别进行处理，然后进行汇总分析［4］.港口企业具有多种投入和产出的复杂性，数据包络分析（data envelopment analysis，DEA）法在处理多输入、多输出问题上具有特别优势且具有较强的客观性［5］.在近期三阶段DEA的研究中，吉生保使用三阶段DEA模型，选用2008年分省数据，对我国高技术产业效率进行了实证研究［6］.王健和梁红艳对我国9家主要港口企业2007～2010年的X－效率进行探索性研究中得出员工人均薪酬、企业规模、腹地经济、企业所有权属性及市场结构是对企业X－效率具有重要影响的外部环境因素的结论［7－11］.

纵观已有的DEA文献，较多使用的是传统DEA模型，但传统DEA模型的最大不足是无法剥离环境效应和随机误差对效率值的影响.为了更准确地测度港口企业的投入产出效率、了解我国港口产业的整体资源利用水平，同时为相关管理人员改进管理、提高效率提供更有力的依据，本文利用可以克服该缺陷的三阶段DEA模型，对2012年我国在上海证券交易所上市的11家港口企业投入产出效率进行实证研究.

使用三阶段DEA模型，第一阶段，构建基于港口企业运营特点的DEA投入产出模型，选择港口营业成本，在职员工数为投入指标，选择港口货物吞吐量和净利润作为产出指标，对决策单元进行投入产出效率分析.第二阶段，采用SFA模型分解各投入指标的松弛变量，剔除环境因素影响和随机扰动影响.第三阶段，利用调整后的投入与原始产出重新运行DEA，研究投入产出效率.

2 效率评价指标设计

2.1 数据来源

选取上港集团、宁波港、大连港、天津港、芜湖港、营口港、日照港、唐山港、锦州港、重庆港九、连云港共11家在上海证券交易所上市的港口企业2012年年报数据作为样本，数据来源于上交所网页公布的上市企业年报.选取的2012年的其他数据，主要来源于《中国统计年鉴2012》《中国港口统计年鉴2012》和中国港口网、交通运输部官方网站以及相应城市与地区2012年国民经济与社会发展统计公报.

2.2 投入产出指标设计

选取货物吞吐量、净利润作为产出指标，营业成本、在职员工数作为投入指标.货物吞吐量是衡量港口企业统计期内，经由水路进、出港区范围并经过装卸的货物重量，是体现港口功能的产出指标；净利润是指在利润总额中按规定交纳了所得税后公司的利润留成，作为产出指标可以较准确地反映企业发展水平和内部管理水平.投入指标中营业成本是指港口企业完成业务或者提供服务的成本；在职员工数是指与企业签订劳动合同的员工人数的总和，营业成本和在职员工数均为企业管理者可以调节的项，当企业投入冗余时，为提高投入产出效率可根据情况进行相应调整.

2.3 环境变量的选取

在第二阶段以营业成本、在职员工数为被解释变量，考虑如下4个环境变量作为解释变量对投入的松弛值进行分解：（1）宏观经济环境的影响，选取港口所在地区当年GDP总量反映企业所处的经济环境；（2）企业规模的影响，选取该企业当年总资产反映企业规模；（3）市场结构的影响，选取市场占有率对投入产出的影响，即该企业的市场占有率＝货物吞吐量／总的货物吞吐量；（4）是否为海港，代表港口生产的自然限制条件，用0—1虚拟变量描述，一般来说，海港条件更好，在相同投入水平下，产出会更高.上港集团、宁波港、大连港等共11家港口企业数据的统计学特征描述见表1.

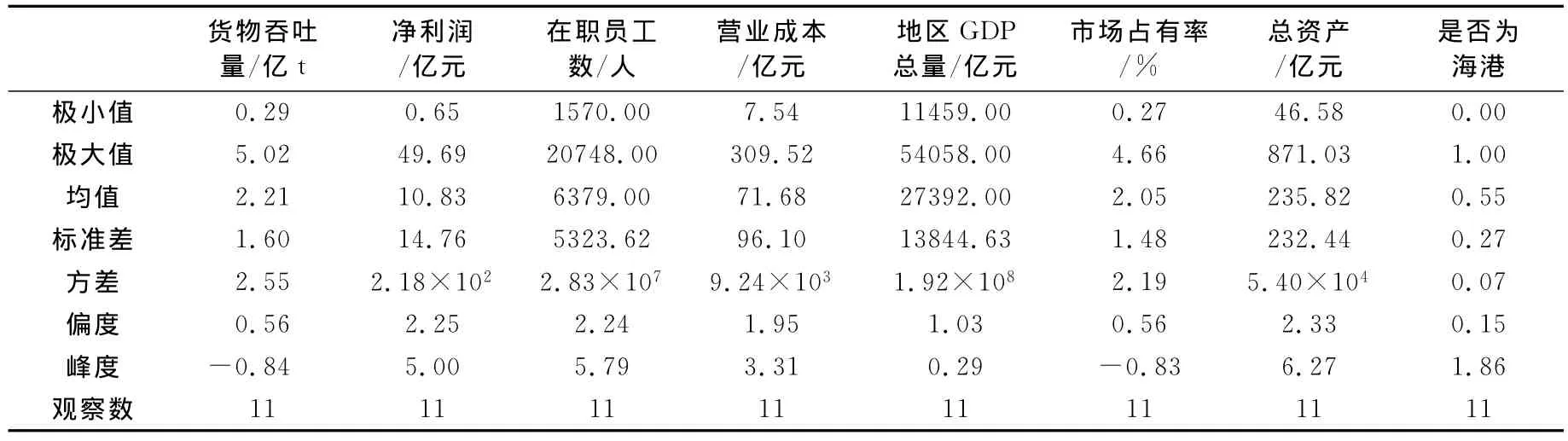
表1 样本数据的统计学特征

3 三阶段DEA模型的构建

3.1 第一阶段DEA

该阶段使用投入产出数据进行一般DEA分析，由于使用DEA中的BCC模型既可以反映规模收益的变化情况，又可以分析总体有效性、技术有效性和规模有效，因此本文采用投入导向的规模报酬可变BCC模型.由于BCC模型是非常成熟的DEA模型，其数学原理已经非常清晰，本文不再赘述.

3.2 第二阶段SFA

假设环境变量数为m，港口数为n，第k家港口的环境变量观测值为zk，则对于第k家港口的第i种投入的松弛变量值sik

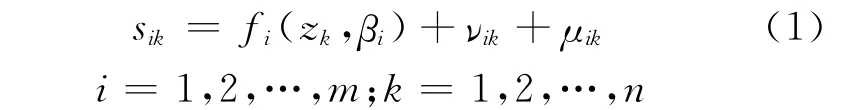
式中：fi（zk，βi）为环境变量对投入差额值的影响方式；νik为反映统计噪声，即随机误差；μik反映管理无效率；νik与μik独立不相关.νik＋μik为组合误差项，本文通过最大似然估计法来估计待估参数βi.

对于管理无效率μik的估计值

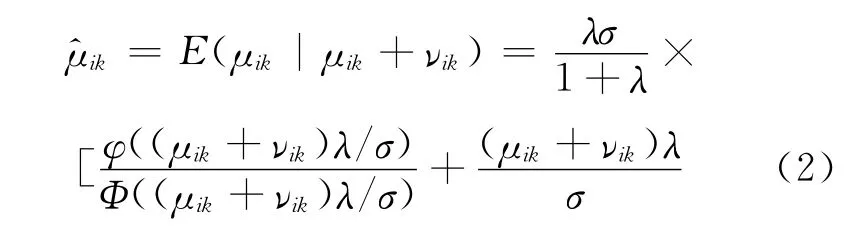
式中：λ＝σμ＋σν；σ2＝；φ和Φ 分别为标准正态分布的密度与分布函数.

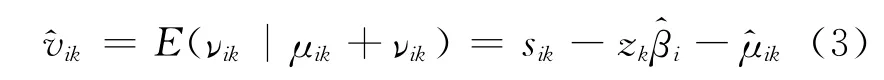
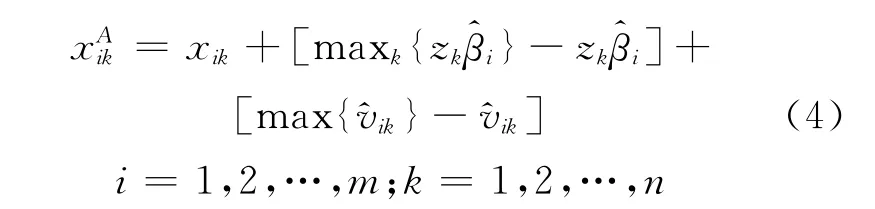
式中：xik为调整前的投入值；zk为环境变量的观察值.这种调整的目的是使各港口企业面临相同的经营环境和运气.

3.3 第三阶段DEA

第二阶段将得到调整后的投入值，将原始产出变量和调整后的投入变量代入第一阶段的DEA模型中，运行得到各决策单元的相对效率值.

4 实证结果分析

4.1 第一阶段DEA模型的实证结果

第一阶段运用DEAP 2.1对我国11个上市港口企业的效率水平与规模报酬进行分析，DEAP 2.1的参数设置为：11个决策单元数（FIRMS），2个投入指标（OUTPUTS），2个产出指标（INPUTS），投入为导向（INPUT ORIENT ATED），可变规模报酬（VRS），多阶段DEA（MULTI－STAGE）.第一阶段 DEAP 2.1的运行结果如表2所列.

表2 第一阶段11家上市港口企业投入产出效率

不考虑环境变量和随机因素的影响，2012年我国上市港口企业综合效率均值为0.740，纯技术效率均值为0.840，规模效率均值为0.856.其中4个港口（大连港、营口港、唐山港、宁波港）3项效率值均为1，处于技术效率前沿，DEA无效的港口的综合的无效率主要来源于纯技术无效率，规模无效率情况相对较轻.

4.2 第二阶段SFA回归分析结果

将第一阶段得出的DMU各投入变量的松弛量作为被解释变量，将地区GDP总量、市场占有率、总资产、是否为海港作为环境变量，构建SFA回归模型，利用软件FRONTIER 4.1进行SFA回归分析.FRONTIER 4.1参数设置为：误差组合模型（ERROR COMPONENTS MODEL），生产函数（PRODUCTION FUNCTION），11个截面数据（NUMBER OF CROSS－SECTIONS），4个解释变量（REGRESSOR VARIABLES）.第二阶段FRONTIER 4.1的运行结果如表3所列.

表3 投入值的松弛变量的SFA回归结果

表3的数据表明，对于在职员工数的松弛变量，环境变量中地区GDP总量影响为负，市场占有率影响为正，总资产影响为负，是否为海港影响为正.对于对于经营成本的松弛变量，环境变量中地区GDP总量影响为正，市场占有率影响为正，总资产影响为正，是否为海港影响为正.

4.3 第三阶段投入调整后的实证结果

将经过第二阶段调整后的各投入变量值和原始产出变量，代入第一阶段DEA模型中，运用DEAP 2.1在原参数设置情况下重新计算各港口企业的效率值，获得的第三阶段各决策单位的投入产出效率值以及规模报酬的状态，第三阶段DEAP 2.1结果见表4.

表4 第三阶段11家上市港口企业投入产出效率

第三阶段计算得到的效率值，由于已经剔除了环境和随机因素的影响，更能相对真实反映出港口企业投入产出效率.考虑外在环境变量和随机因素影响，2012年我国上市港口企业综合效率均值为0.722，纯技术效率均值为0.876，规模效率均值为0.809.其中4个港口（大连港、营口港、唐山港、宁波港）3项效率值均为1，处于技术效率前沿.连云港综合效率为0.310相较与DEA有效值1差距较大，连云港纯技术效率0.558相较与DEA有效值1差距较大，重庆港九规模效率0.483相较与DEA有效值1差距较大.

调整前后的投入产出效率均值对比可以看出，剔除环境变量和随机因素的影响后，上市港口企业的综合效率、规模效率有所下降，纯技术效率有所提高，其中综合效率由0.740下降到0.722，规模效率由0.856下降到0.809，纯技术效率由0.840上升到0.876.并且规模效率的降低幅度5.8%要高于纯技术效率的提高幅度4.1%，而综合效率的降低主要源于规模效率的下降.

5 结论与建议

2012年我国上市港口企业综合效率均值、纯技术效率均值、规模效率均值较高，港口业整体处在一个健康发展的状态上.

对于港口投资者，上港集团规模报酬递减，应该减少投资；日照港、天津港、重庆港九、锦州港、芜湖港、连云港共6个港口属于规模报酬递增，具有一定的规模经济效益，可适当考虑增加投资，扩大港口规模.宁波港、大连港、营口港、唐山港4个港口规模报酬不变，应该控制投资.港口规模不是越大越好，需要控制在一定范围，这符合经济学的适度规模理论.

对于港口经营者，处在随机前沿面上的港口企业，其在港口的经营管理上，具有一定的借鉴作用.港口运营者可对本企业进行具体的投入产出分析，对企业内部的运营、管理等多个方面寻找突破点，减少投入；也可在现有的投入水平下，积极寻找扩大产出的途径和方法，提高投入产出效率.

［1］张 哲，张 闯，朱 宏.钢铁企业电子商务营销的模糊评价［J］.工业工程与管理，2006（3）：58－63.

［2］徐广业，但 斌.肖 剑.交互式DEA－AHP模型及其应用［J］.系统工程学报，2011，26（2）：262－268.

［3］李志红，和金生.基于AHP－SFA的人力资源外包供应商绩效评价模型研究［J］.经济问题，2010（4）：74－77.

［4］韩 晶.中国高技术产业创新效率研究：基于SFA方法的实证分析［J］.科学学研究，2010（3）：467－472.

［5］钟 华，汪凌勇.DEA方法在R＆D绩效评估中的应用研究［J］.科技管理研究，2008（3）：86－93.

［6］吉生保，周小柯.基于三阶段DEA模型的中国高技术产业效率研究［J］.中央财经大学学报2010（12）：62－66.

［7］王 健，梁 红.基于三阶段DEA模型的我国主要上市港口企业X－效率研究［J］.福州大学学报：哲学社会学版，2012（3）：19－26.

［8］晏华辉，崔晋川.基于AHP与DEA的多因素排序法［J］.系统工程学报，2004（5）：543－547.

［9］WANG Y M，LIU J，ELHAG T M S.An integrated AHP／DEA methodology for bridge risk assessment［J］.Computers and Indnstrlal Engineering，2008（3）：513－525.

［10］迟国泰，杨 德，吴珊珊.基于DEA方法的中国商业银行综合效率的研究［J］.中国管理科学，2006（5）：52－61.

［11］KAO C，LIU S T.Stochastic data envelopment analysis in measuring the efficiency of Taiwan commercial banks［J］.European Journal of Operational Research，2009（1）：312－322.