色谱指纹图谱欧式距离法的一种改进

闫 艳， 孟庆华， 李广超， 张桂芝

（江苏师范大学化学化工学院， 江苏 徐州 221116）

色谱指纹图谱欧式距离法的一种改进

闫 艳， 孟庆华*， 李广超， 张桂芝

（江苏师范大学化学化工学院， 江苏 徐州 221116）

目的 通过对欧氏距离算法的改进构建相对欧氏距离，使其值能够精确地反映样品指纹图谱与对照指纹图谱的相似性。方法 以对照指纹图谱为标准建立样品及对照比值指纹图谱，并将样品与对照品指纹峰向量差值和的绝对值和向量差绝对值的和的比值和各共有峰、非共有峰总面积的权重系数引入欧氏距离计算公式，并计算指纹图谱向量模长的比值，利用文献数据评价参麦注射液质量和中药材大黄质量。结果 模拟数据计算结果表明改进算法能准确反应指纹图谱峰间比例关系的一致性及共有峰总面积的波动，定量反应非共有峰总面积对相对欧氏距离的影响.参麦注射液和大黄指纹色谱的计算结果与文献一致。结论 本文提出的相对欧氏距离计算方法和判断方法可用于中药产品批间质量稳定性的控制。

指纹图谱；欧式距离；质量评价；参麦注射液；大黄

指纹图谱技术是目前公认的全面控制中药、食品等复杂成分体系质量的最有效可靠的技术。指纹图谱质控技术进行质量控制的关键是相似度评价理论及其软件化。色谱指纹图谱相似度评价的实质是考察要比较的两个指纹图谱的组成峰数、峰匹配以及相应峰量化关系的一致性：即一方面从产品质量的稳定性和一致性考虑，相似度大小应能灵敏反映多元化学成分分布比例的差异和整体含量的差异；另一方面从安全性考虑，相似度大小应能考察非共有峰总面积大小对相似度的影响。有关色谱指纹图谱相似度评价方法研究已取得了一定的进展，文献报道的 主 要 有 峰 重 叠 率［1］及 作 者 提 出 的 改 进 方法［2］、向量夹角余弦［3］、 相关系数［4］、组合相似度［5］、基于相 似 系 统 理 论 的 多 种 程 度 相 似 度［6-8］、总量 统 计 矩 相 似 度［9］、 距 离 相 似 度 包 括 马 氏 距离［10］、 欧氏距离［11-13］、 欧马距离［14］、 指数 相似系数法［15］、 以及用相对熵的歧异值来衡量色谱指纹图谱的相似度［16］等方法， 文献 ［17］ 提出了比率定性相似度及投影含量相似度等多个特性指标用于中药质量的控制。这些相似度评价方法各有特点，但也存在各自的局限性［18］， 不能完全满足指纹图谱对中药质量控制的实际应用要求，如相关系数、夹角余弦法等相似度不能灵敏地反映小峰的变化和丢失，也不能反应图谱上色谱峰总面积的波动变化；基于相似系统理论的多种程度相似度，不能反映非共有峰 （不能与对照指纹图谱相匹配的峰）峰值大小对相似度的影响，其计算的相似度大小顺序有时与峰值比例的变化趋势并不一致；组合相似度是在共有峰的夹角余弦相似度基础上纳入了非共有峰的影响，但存在样本增加或改变时需重新计算合适的 ω范围的问题［5］； 欧马距离尽管克服了马氏距离对变化微小变量的作用放大的缺点，但依然和马氏距离一样存在要求总体样本数大于样本的维数，另一方面即使满足了总体样本数大于样本的维数的条件，但是有些情况下存在无法求出协方差矩阵的逆矩阵的可能。绝对欧式距离数值大小尽管存在受变量单位不同以及检测器响应不同的影响［19-20］， 但绝对 欧 氏 距 离 没 有 马 氏 距离存在 的 上述问题，同时 （与夹角余弦等相似度算法比较而言）具有能同时反映中药多元化学成分分布比例的差异和色谱峰总面积的差异，也能考察非共有峰峰值大小对相似度影响的性能［19］， 因此本研究基于分子分母只要取相同计量单位，其比值大小与分子分母计量单位无关的原理，结合以对照指纹图谱为计算参照标准，采用比值法对数据进行预处理，以修正的待比较样品指纹图谱和对照指纹图谱间的欧氏距离与对照指纹图谱向量模长的比值来计算指纹图谱间的相似性，本研究称之为相对欧式距离，由于相对欧式距离是绝对欧氏距离相对对照指纹图谱模长求得的比值，消除了绝对欧氏距离存在的上述问题，数值大小具有直观的综合定量评价能力，能够反映指纹峰的相关性、峰比例关系的变化和色谱峰总面积的波动，定量地反映非共有峰总面积大小的影响； 本研究还根据箱线图法 （ Box Plot） 原理［21］提出了确定相似性判断阈值的经验方法， 便于根据相似度大小从质量均一性、稳定性与安全性上控制药品、食品的质量。

1 新相似度算法的原理

1.1 相似度算法的提出 本研究构建的相似度算法是基于事先确定的对照指纹图谱为计算参照标准；以中药色谱指纹图谱峰面积值或峰高为相似度评价信息参数；以图谱矢量化空间模式向量间相似性计算为基本出发点。

图1 样品指纹图谱和对照指纹图谱向量图Fig.1 Vectors of sam p le fingerp rint and standard fingerprint

1.2 相似度算法的优化 当样品指纹图谱色谱峰比对照指纹图谱对应峰都偏大时，样品与对照样品的化学成分分布比例较一致，而如果样品指纹图谱色谱峰比对照指纹图谱对应峰一部分偏大另一部分偏小时，二者的化学成分分布比例相差较大，采用式 （1） 计算上述两种情况的相似性时不能灵敏反应这种差异， 必须对公式 （1） 进行修正， 修正后的计算方法见公式 （2）。

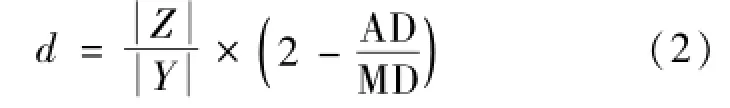
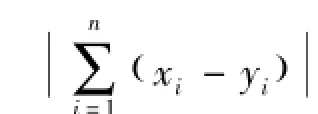
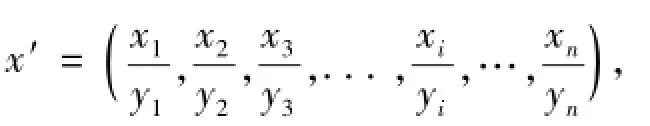
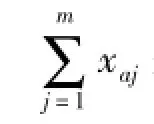
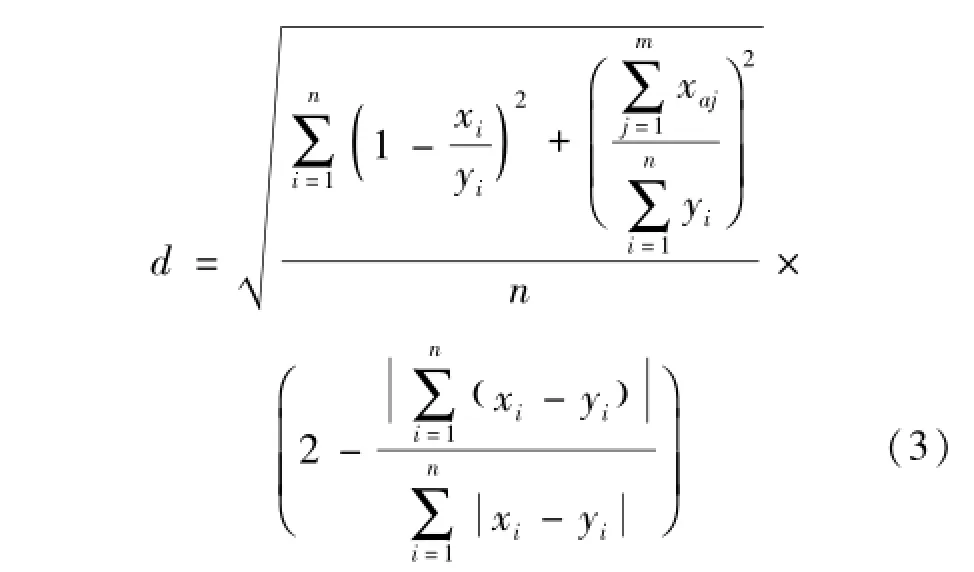
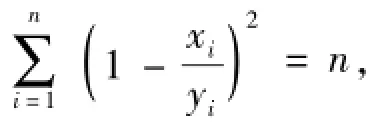
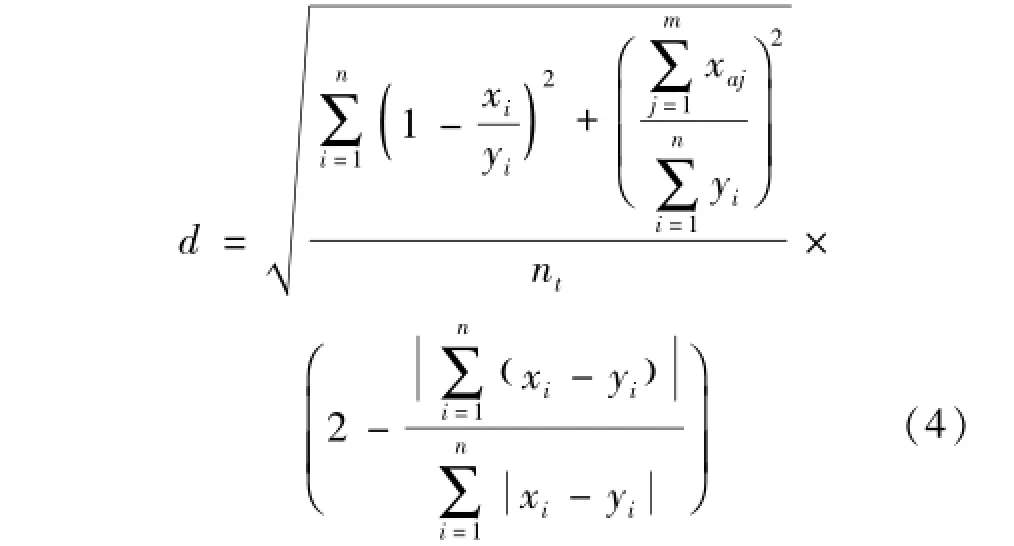
由于中药组成成分复杂，各成分的结构及药效等不尽相同，故对中药指纹图谱相似性评价时，各成分可能存在有不同的比重系数。为此，实际应用时可考虑根据药效、毒性研究等确定中药不同成分相似性评价的药效影响因子，对指纹图谱相似性评价中的特征变量进行加权运算。加权运算公式为公式 （5）：

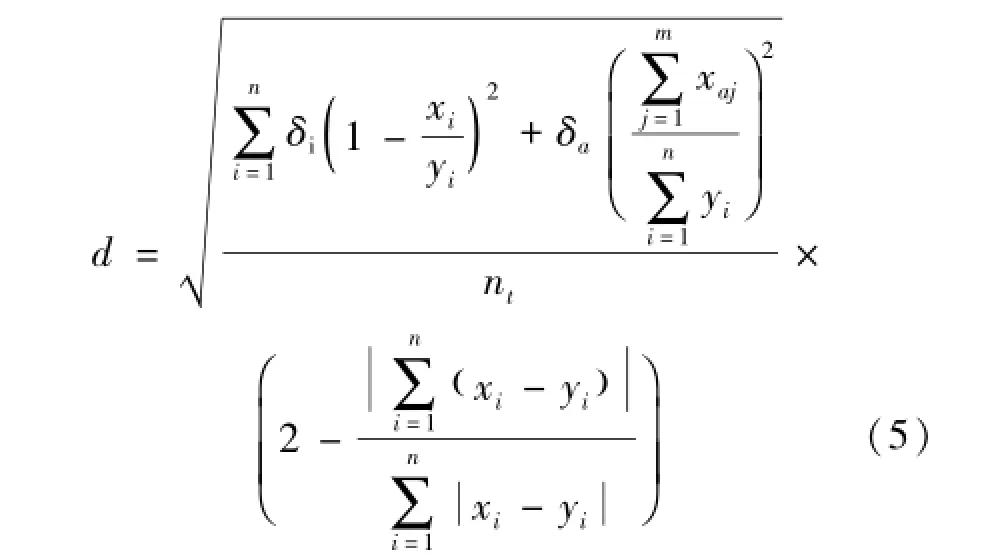
式中 δi、δa分别是各共有峰、 非共有峰总面积的权重系数， 权重的取值范围 δi≥0 或 δa≥0， δi、δa取值原则是： ①向量的各维变量对产品有效性安全性影响不明确时 δi及 δa可全取 1；②某些变量对产品有效性安全性影响非常明显时 δi＞1 或 δa＞1，具体大小通过实验确定；③某些变量对产品有效性安全性影响较小时 1 ＞δi≥0 或 1 ＞δa≥0，具体大小通过实验确定。 确定 δi、δa大小的具体试验方法有待进一步研究。

1.3 相似度判断阈值 d限的确定方法 公式 （4）用于判定中药批次间产品质量是否稳定的实际应用时，需要确立一个科学合理的相似度评价阈值；阈值的确定前提是必须首先确定对照指纹图谱，这显然要事先选择一些已鉴定好的合格的中药产品样本并获得其相应的中药色谱指纹图谱；合格品的最终选择只有通过有效性、安全性试验确定，目前的指纹图谱技术发展水平还难于实现。根据本实验室对试验数据和文献数据计算验证经验，提出一种结果较可靠、操作性较强的经验方法：①根据专家经验或其他方法选择不少于 10个批次的正品药材或中药制剂产品；②采用计算机技术对这些正品药材或中药制剂产品的指纹图谱数据进行预处理和色谱峰匹配；③对被保留的药材或中药制剂产品的指纹图谱用平均矢量法或中位数矢量法，优选稳健性较好的中位数矢量法初步建立该产品的对照指纹图谱；④用式 （4） 计算被保留的每个正品药材或中药制剂产品的指纹图谱与初步确定的对照指纹图谱相似度的 Syj；⑤ 根 据 箱 线 图 法 （ Box Plot） 原 理［21］，对 dyj数据按从小到大排序， 并求出该序列数据的统计量第一四分位数 Q1、 第三四分位数 Q3， 并求出这两个四分位数差值 df=Q3-Q1， 将所有 Syj数据与 Q3+1.5df比较， 所有大于 Q3+1.5df的 dyj数据判断为异常值而将对应药材或中药制剂产品剔除， 重复③ ～⑤步， 直至 dyj系列不再出现异常值；⑥被保留药材或中药制剂产品的指纹图谱的按③步确定最终对照指纹图谱， 按④步计算的 dyj系列，其中的最大值即为 d限。

2 数据来源、 数据处理方法及程序

本研究以模拟数据计算结果研究比较相似性新算法及其他相似度算法的性能，并将本研究提出的方法应用于文献指纹图谱数据， 相关计算采用 matlab 软件 （Mathwork Inc.）自行编写程序。

3 结果与讨论

3.1 定性比较新算法与其他相似度算法 假设有某一产 品 的对照指纹 图 谱向量和 3 个 待比较样品指纹图谱 向 量如 图 1b 所 示，、是 3 个样品 指 纹 图谱向量与的差向量，分 别表示向 量之间的欧氏距离向 量在向量的投影是在 向 量上 的 投 影，表 示 向 量的 模长，表 示 向量的模长。 从 图 1 可以

3.2 定量比较新算法与其他相似度算法 表 1 是采用差异明确的模拟数据来考察4种相似度的计算结果。表中对照样品假设有6个色谱峰，各峰值大小依次为 1、 5、 10、 15、 20、 25； 1 ～6 号样品是对对照样品稀释或浓缩不同倍数的样品，稀释或浓缩的倍数分别为 0.5、 0.9、 1.1、 1.5、 2.0 和3.0；7 ～12 号样品除含对照样品中种类相同浓度相同的6个成分外，还多出一个对照样品中没有的非共有成分， 非共有成分的峰大小依次由 1 变为 25；13号样品与3号样品各峰值大小相对于对照样品各峰的差异都为 10%， 但变化方向不同， 3 号样品所有峰都比对照指纹图谱峰偏大， 而 13 号样品比对照指纹图谱峰后三个峰偏大， 前三个峰偏小； 14号样品的二号小峰与 15 号样品的六号大峰相对对照指纹图谱的相对差异相同， 都为 10%， 其余峰值与对照样品对应峰大小相同； 16号样品的二号小峰与17号样品的六号大峰相对对照指纹图谱的绝对差异相同，都为3， 其余峰值与对照样品对应峰大小相同。

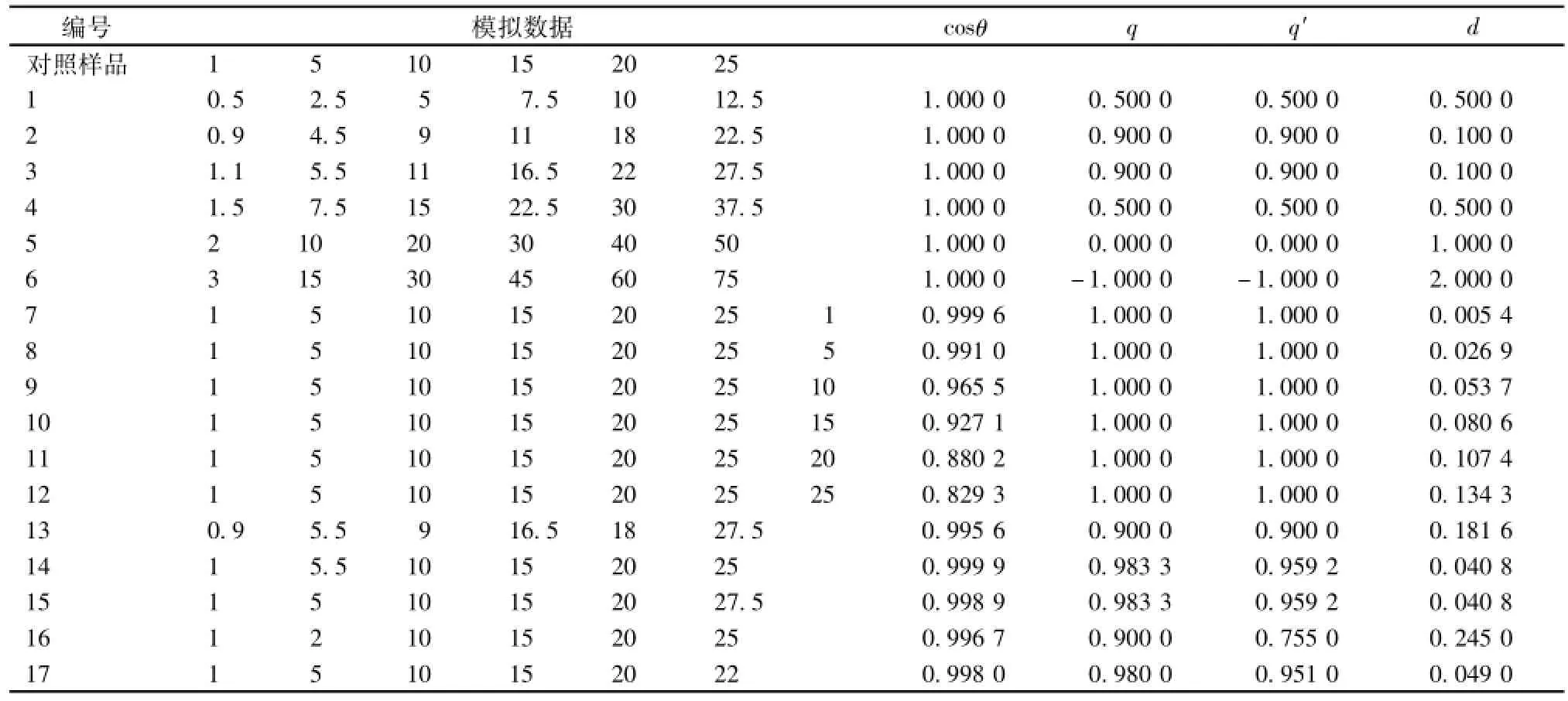
表1 用4种相似度算法计算的模拟数据相似度结果Tab.1 Resu lts of four sim ilarity algorithm s based on simulated data

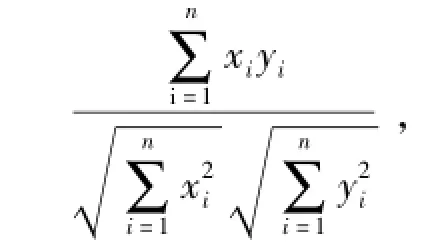
表1中1～6号样品的相似度数据表明当峰值大小的总差异不超过 100%时， 本研究定义的相对欧氏距离d的数值大小与样品和参照样品的相对平均差异大小一致， 而改良程度相似度 q、 新改良程度相似度 q'数值大小与样品相对参照样品的相对含量一致，从不同角度都能给出直观的综合定量评价结果； 即使相对差异超过 100%， 数值的大小也能反映样品和参照样品的差异，本研究计算的相对欧式距离越大，样品与对照样品的差异越大；而夹角余弦相似度 cosθ全为 1， 不能反应样品与参照样品的这种总量的差异。 7 ～12 号样品与对照样品非共有峰峰值由1 变为25时， 本研究定义相对欧氏距离 d 由 0.005 4 变化为 0.134 3； 夹角余弦相似度cosθ由 0.999 6 变化 0.829 3； 表明相对欧氏距离d、 夹角余弦相似度 cosθ都能定量地反映非共有峰峰大小的影响，而改良相似度q及新改良程度相似度 q'由于只能反应共有峰的变化对相似度的影响，相似度全为 1。相对于对照指纹图谱而言，13 号样品峰比例关系的一致性比3号样品峰比例关系的一致性要差， 按公式 （3） 计算的相对欧氏距离 d13号样品的 0.181 6 大于 3 号样品 0.100 0， 与实际一致且二者的相对欧氏距离 d的差值△d比夹角余弦值差值大，而改良程度相似度q及新改良程度相似度 q'不能反映这种差异。 表 1 中 14 号、 15 号样品相似性数据表明按公式 （4） 计算的相对欧氏距离d无论大峰还是小峰，只要相对差异相同对性的影响是一样的，而夹角余弦值对大小峰的灵敏度是不同的。 16 号、 17 号样品相似度数据表明按公式（4） 计算的相对欧氏距离 d 能灵敏反应大小峰产生相同的绝对差异时对相似性不同的影响， 对16号样品小峰的绝对差异为 3 时相对差异为 60%，而17号样品大峰的绝对差异为 3 时相对差异为12%，因此 17 号样品的相对欧氏距离 0.049 0 小于 16 号样品的相对欧氏距离 0.245 0。上述结果表明：本研究建立的指纹图谱相似度算法既能灵敏反映指纹图谱各成分含量比例的变化，也能反映总量的变化及非共有峰的影响，且无论对大峰还是小峰都表现出较高的敏感性。

3.3 计量单位以及检测器不同的响应对相对欧氏距离的影响 相同条件下同一样品指纹图谱色谱峰面积或峰高大小与采用的计量单位有关，但不同的计量单位间存在一定的换算系数 k，假设yi由某已计量单位换算成另一计量单位，数值大小变为kxi、代入式 （4） 整理如式 （6）， 显然 d 值与k无关。尽管不同仪器不同的检测器响应不同，检测器间响应值比是固定不变的，这类似于峰值计量单位的不同情况，检测器不同响应对d值大小理论上没有影响，甚至采用适当方法测量出不同检测器间比值对不同仪器获取数据校正后，不同仪器获取数据可通用。

3.4 新算法评价中药制剂质量稳定性的应用 表2 是文献 ［10］ 中 23 个参麦注射液样品指纹图谱数据及采用式 （4）计算的相对欧氏距离结果；1 ～11 号是以工艺 A制得的参麦注射液样品， 作为合格品， 12 ～17 号以工艺 B制得的参麦注射液样品， 2’、 3’、 4’、 5’、 9’ 号是 2、 3、 4、 5、 9 号参麦注射液样品的重复进样获得的指纹图谱， 18号是以西洋参代替红参所作的伪品；对照指纹图谱是以中位矢量法用 1 ～11 号样品指纹图谱数据确定的。 根据本研究确定相对欧氏距离判断阈值 d限的方法， 发现7号样品和 11 号样品为异常样品， 剔除 7、 11 号样品后， 将 1 ～6 号、 9 ～10 号作为合格样本，以中位法重新确定对照指纹图谱，依次以公式 （4）计算 1 ～6 号、9 ～10 号、 2’、 3’、4’、5’、 9’号、 7 号、 11 号及 12 ～18 号样品相对新对照指纹图谱的相对欧氏距离，结果按顺序为0.232 9、 0.197 1、 0.202 8、 0.437 3、 0.094 8、0.303 6、 0.345 1、0.237 8、0.188 2、0.222 9、0.197 6、 0.421 7、0.102 8、0.239 5、0.975 3、0.718 8、 2.132， 2.700， 2.941， 1.939 3， 3.726，3.263， 11.89； 1 ～6 号、 9 ～10 号合格样本的相对欧氏距离未发现异常值，4号样本的相对欧氏距离0.437 3 为最大， 确定为判断阈值 d限； 显然 12 ～18号相对欧氏距离 d 值均大于 0.437 3， 可判定为不合格品 （工艺 B与工艺 A有显著差别）， 2’、 3’、 4’、5’、 9’ 号相似度的均小于 0.437 3， 可判定为合格品，特别是 18 号伪品其相对欧氏距离最大为 11.89，按新的阈值 d限判断， 7、 11 号样品依然为异常样品，分析7、 11 号样品指纹图谱数据可发现， 二者的指纹图谱第一个色谱峰值分别为 2.72、 3.05， 明显比其他合格样本对应峰值大得多，说明判断是合理的；即使在剔除 7、 11 号样品前计算的相对欧氏距离，从表1 的数据也可以看出1 ～11 号样本的相对欧氏距离也远小于 12 ～18 号样品的相似度， 表明公式（4） 算法计算的相对欧氏距离能够反应两种不同工艺的差别， 从另一个角度说明公式 （4） 算法计算能够反应中药制剂质量的稳定性均匀性。

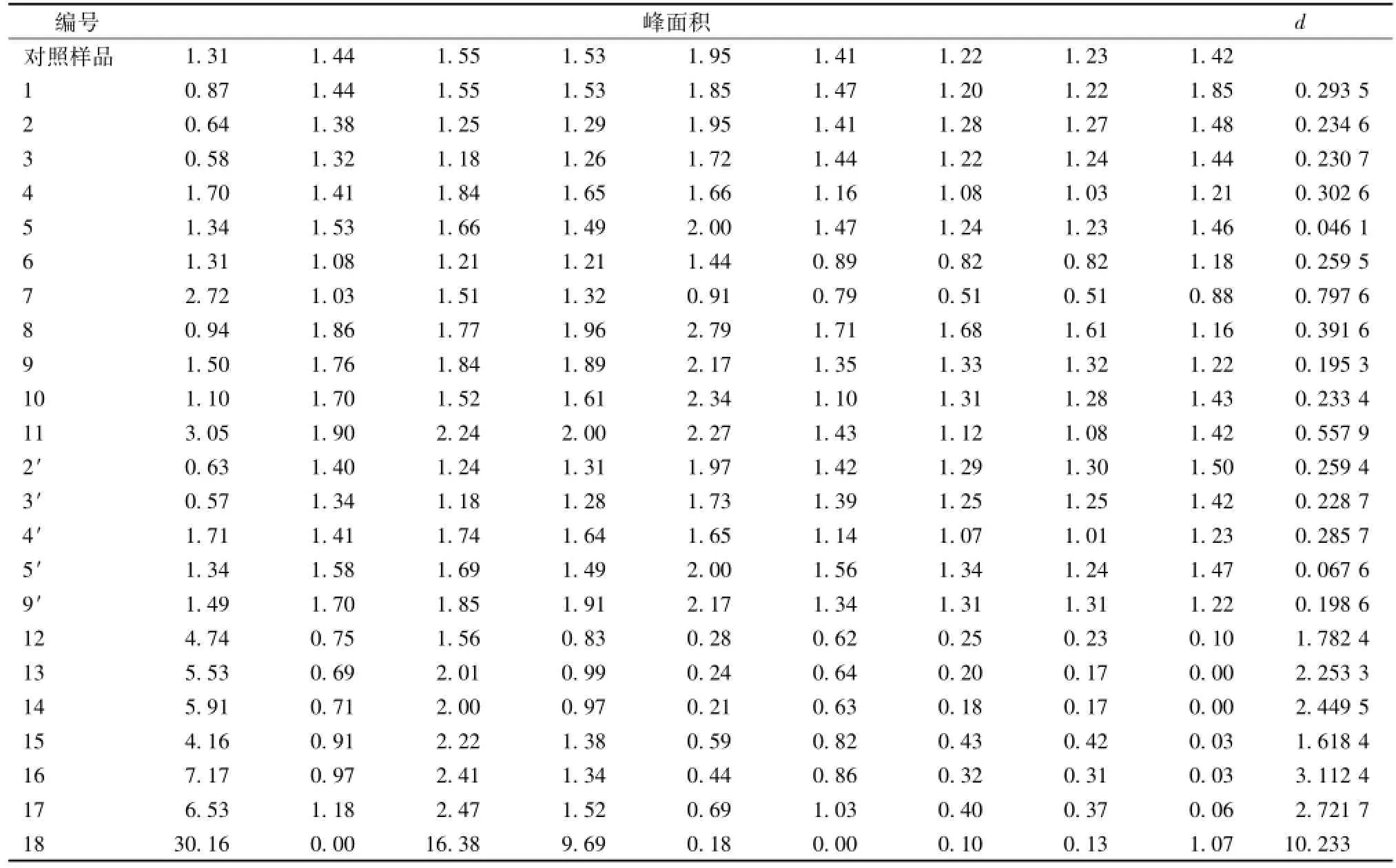
表 2 18 批参麦注射液指纹图谱数据及相对欧式距离相似度结果Tab.2 Data of chromatographic fingerprints of 18 batches of Shenmai Injection and results of their sim ilarity

3.5 新算法评价中药材质量优劣的应用 表 3 是文献 ［22］ 中 19 个大黄样品的指纹图谱数据及采用公式 （4） 计算的相对欧氏距离 d 结果。 1 ～5号、 8 ～11 号样本在原始文献中定为正品大黄样品， 6、 7 号及 12 ～19 号是待鉴定大黄样品， 表中对照指纹图谱是按 “3.3” 节同样的方法剔除 4 号样本后以1 ～3 号、 5 号、 8 ～11 号为合格样本指纹图谱数据用中位矢量法确定的。根据本研究提出的相对欧氏距离判断阈值 d限的确定方法， 1 ～3 号、 5号、 8～11 号相对欧氏距离无奇异值， 最终确定大黄相对欧氏距离的阈值 d限为 1.904 3； 显然 6、7 号样品相对欧氏距离 d 值均小于 1.904 3， 可判定为合格品； 12 ～19 样品相对欧氏距离 d 的值均远大于1.904 3， 可判断它们属非合格品， 这与文献6、 7 号为正品， 12 ～19 为非正品的结论是一致的。尽管原文献把4号样品作为正品大黄，但4号样品的指纹图谱数据表明， 其第 10 个和第 14 个色谱峰面积（分别为 94.4、 28.1） 比其他正品大黄对应色谱峰远远大得多 （对照指纹图谱相应峰面积分别为8.90、 1.40）， 说明其内在化学成分与其他正品大黄有显著差异，剔除是合理的。上述数据表明本研究构建的相对欧氏距离算法可用于中药材质量控制。

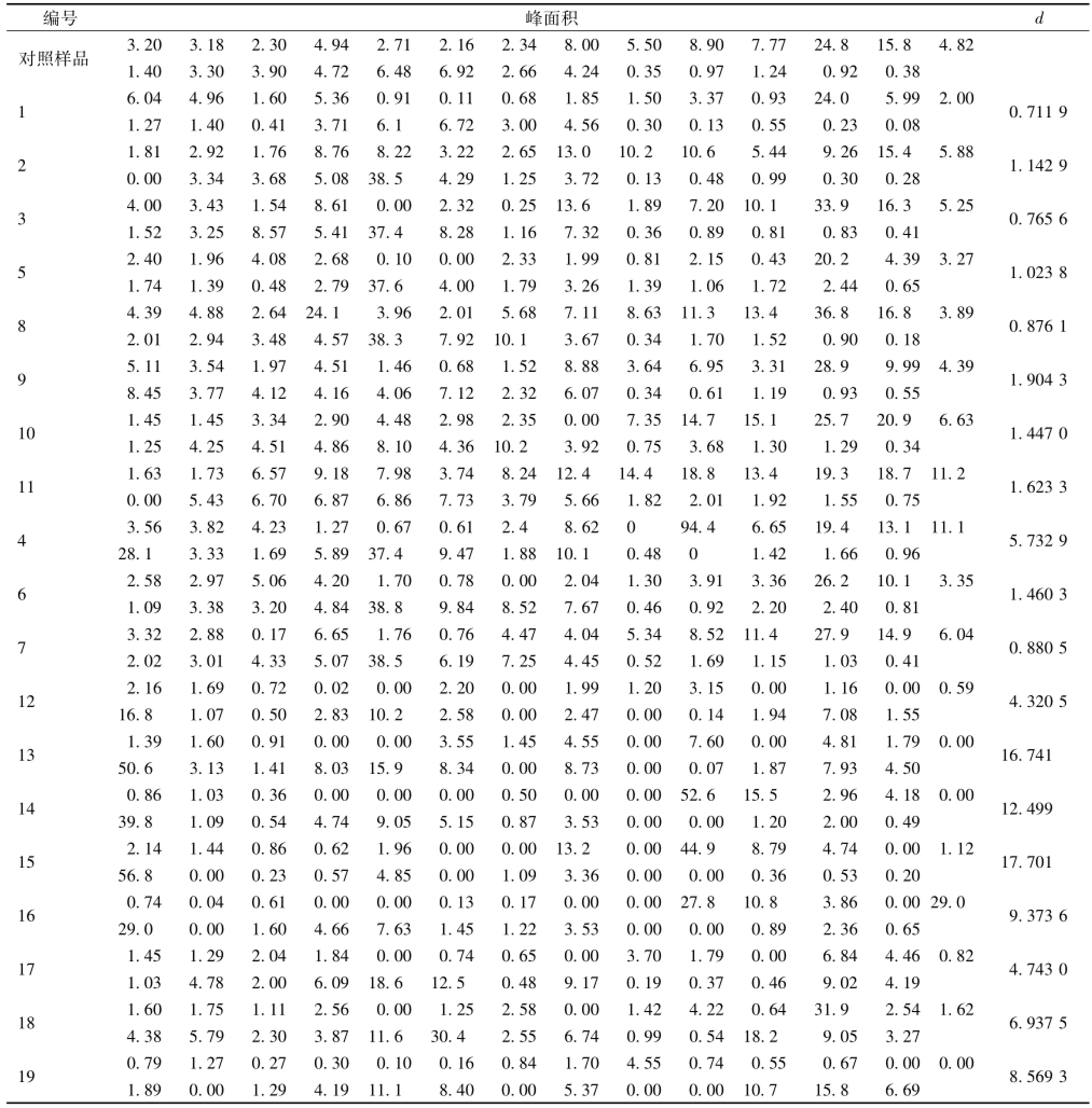
表 3 19 批大黄药材指纹图谱数据及相对欧式距离相似度结果Tab.3 Data of chromatographic fingerprints of 19 batches of Rhei Radix et Rhizoma and results of their sim ilarities

4 结论

综上所述，模拟数据计算结果显示本研究构建的相对欧氏距离算法不仅能够准确灵敏地反应指纹图谱共有峰峰分布比例关系的变化和峰面积总量的波动，也能够定量反应非共有峰总面积大小对相似度的影响，具有较好的综合评价能力；本研究根据箱线图法原理提出的确定相对欧氏距离判断阈值的经验方法具有较强的可操作性和实用性，利用文献数据对参麦注射液质量和药材大黄质量的评价结果表明方法可用于中药产品批次间质量的均一性、稳定性和安全性评价；数据显示用于中药材的相对欧氏距离判断阈值比中药制剂的相对欧氏距离判断阈值要大，主要由于中药材内在化学成分是次生代谢产物受各种因素影响变化较大，而中药制剂经生产工艺过程的控制，内在化学成分质量较均一稳定，这本就是中药指纹图谱质控技术的目的所在，显然利用本研究提出的方法能够筛选出质量更为稳定的原药材，更有利于中药质量稳定可控。

［ 1］ 洪筱坤， 王智华.中药数字化色谱指纹谱［M］.上海： 上海科学技术出版社， 2003： 82-83.

［2］ 孟庆华，刘永锁，王健松，等.色谱指纹图谱相似度的新算法及其应用［J］.中成药， 2003， 25（1）： 4-8.

［3］ 王龙星，肖红斌，梁鑫淼，等.一种评价中药色谱指纹谱相似性的新方法： 向量夹角法［ J］.药学学报， 2002， 37（9）： 713-717.

［4］ 田润涛， 谢培山.色谱指纹图谱相似度评价方法的规范化研究 （一） ［J］.中药新药与临床药理， 2006， 17（1）： 40-42， 54.

［5］ 詹雪艳，史新元，段天璇，等.色谱指纹图谱组合相似度的算法［ J］ .色谱， 2010， 28（11） ： 1071-1076.

［6］ 刘永锁，孟庆华，蒋淑敏，等.相似系统理论用于中药色谱指纹图谱的相似度评价［J］.色谱， 2005， 23（2）： 158-163.

［7］ 刘永锁，曹 敏，王义明，等.相似系统理论定量评价中药材色谱指纹图谱的相似度［J］.分析化学， 2006， 34（3）：333-337.

［8］ 詹雪艳，史新元，展晓日，等.基于相似系统理论的相似度计算方法的改进［ J］.分析化学， 2010， 38（2） ： 253-257.

［9］ 贺福元，周宏灏，邓凯文，等.指纹图谱的一种定性定量研究新方法_ 总量统计矩分析法［J］.药学学报， 2008， 43（2）： 195-201.

［10］ 吴 昊， 田燕华， 郭平平， 等.多元统计学在参麦注射液指纹图谱中的应用［J］.中成药， 2002， 24（1）： 3-6.

［11］ 叶 皓， 沈 顺， 张祥民.液相指纹图谱结合欧氏距离对野菊花质量控制的研究［J］.世界科技研究与发展， 2006，28（2）： 72-74.

［12］ 李希强， 陆舍铭， 王 笛， 等.烟用香精 UPLC指纹图谱的夹角余弦、 相关系数与欧氏距离评价［J］.烟草科技，2008（12）： 37-41.

［13］ 李希强， 王 笛， 陆舍铭.夹角余弦与欧式距离相结合建立烟用香精 HPLC指纹图谱［J］.香料香精化妆品， 2007，（6）： 26-30.

［14］ 赵曰利， 于宏晓， 宗兆奇， 等.欧马距离法在香料指纹图谱模式识别中的应用［J］.烟草科技， 2011（2）： 52-57.

［15］ 谷瑞敏， 郭治昕， 刘巍巍， 等.中药色谱指纹图谱相似度评价新模型及其论证［ J］ .中成药， 2009， 31（1） ： 1-4.

［16］ 王 康， 杜 凯， 李 华.相对熵方法用于中药指纹图谱相似度计算［ J］.计算机与应用化学， 2007， 24 （1）：49-52.

［17］ 孙国祥， 侯志飞， 张春玲， 等.色谱指纹图谱定性相似度和定量相似度的比较研究［J］.药学学报， 2007， 42（1） ：75-80.

［18］ 关洪月， 李 林， 刘 晓， 等.中药指纹图谱相似度计算方法探析［J］.中国实验方剂学杂志， 2011， 17（18） ： 282-287.

［19］ 吴玉田， 柴逸峰.药物分析信息学及应用［M］.北京： 人民卫生出版社， 2009： 143.

［20］ 聂 磊， 曹 进， 罗国安， 等.中药指纹图谱相似度评价方法的比较［J］.中成药， 2005， 27（3）： 249-252.

［21］ 庄作钦.BOXPLOT_ 描述统计的一个简便工具［ J］.统计与预测， 2003， 2： 56-57.

［22］ 洪筱坤， 王智华， 李 旭.HPLC-相对保留值指纹图谱鉴别大黄［J］.中国中药杂志， 1993， 18（11）： 650-652.

Im provement of Euclidean distance between chromatographic fingerprints

YAN Yan， MENG Qing-hua*， LIGuang-chao， ZHANG Gui-zhi
（School of Chemistry&Chemical Engineering， Jiangsu Normal University， Xuzhou 221116， China）

AIM To improve the algorithm of the relative Euclidean distance in order to accurately reflect the similarities between chromatographic fingerprints of herbs.METHODS The ratio of sample and reference chromatographic fingerprintswere established for reference standard of chromatographic fingerprints.The absolute value of the sum of the vector difference and the sum of absolute value of the vector difference of sample and reference chromatographic fingerprints and the weight coefficients of common peaks and non common peakswere brought into the calculation of Euclidean distance，and their norm of vector.Lecture data of Shenmai Injection and Rhei Radix et Rhizoma were served as the computation.RESULTS The improved algorithm could reflect the uniformity of peak area ratios and fluctuation of total peak areas and quantified the influence of non common peaks on relative Euclide-an distance.The data from algorithm applied to the chromatographic fingerprints of Shenmai Injection and Rhei Radix et Rhizoma were consistentwith the lecture data.CONCLUSION The algorithm may be applicable for the quality evaluation of differentbatches of herbal preparations.

fingerprints； similarity；Euclidean distance；quality evaluation； Shenmai Injection；RheiRadix et Rhizoma

R284.1

： A

： 1001-1528（2014）05-1012-09

10.3969/j.issn.1001-1528.2014.05.028

2013-06-04

江苏省徐州市科技发展基金 （XF10C015）

闫 艳 （1987—） ， 女， 硕士， 从事药品分析研究。 Tel： （0516） 83403165， E-mail： 571472309@qq.com

*通信作者： 孟庆华 （1965—） ， 男， 博士， 副教授， 研究方向： 中药质量控制。 Tel： （0516） 83403165， E-mail： mqhxz@126.com