大行程柔性铰链Hexapod机构参数优化设计
彭 程,殷跃红(上海交通大学机械与动力工程学院,上海200240)
0 引言
光学系统在光学显微镜、半导体生产和空间探测等超精密工程领域中得到了广泛的应用[1]。为了保证光路的准确性,光学元器件不但需要有很高的面形精度,而且需要精密的定位系统。以大口径空间望远镜的子镜拼接为例,在戈达德太空飞行中心研制的太空球面光学望远镜主镜[2](SPOT)直径3.5m,由6个对角线长0.86m的六角形子镜环状排列组成,中心无镜面。每个子镜都有倾斜、翻转和移动的自由度,SPOT对每个子镜的定位精度提出了很高的要求:镜面法向移动范围目标值±5mm、最小值±1mm,镜面法向移动分辨率目标值<10 nm、最低值20nm。镜面翻转范围±2°,镜面翻转分辨率≤0.05arcsec。
传统的光学元器件精密定位并联机器人使用的是球铰、万向铰链等传统的运动副作为活动关节,会引入摩擦、回程间隙和爬行等问题极大地影响并联机器人的精度。为了克服使用传统运动副引起的上述问题、减小并联机构的精度损失,柔性铰链被用来作为新型并联机器人[3-5]的运动副。柔性铰链具有结构简单、无摩擦和精度高等优点,能够使系统得到很高的精度和分辨率。然而,由于柔性铰链的变形量有限,传统的全柔性铰链的并联机器人的工作空间都很小,多在立方微米级。在一些需要较大行程的应用中往往需要两级运动机构的叠加,其中一级提供较大范围的运动,另一级为微位移的柔性并联机构。这样的结构增加了系统的复杂性,提高了系统成本。为了使得柔性铰链并联机器人能够在立方厘米级的工作空间得到应用,近年来又开发了大行程的柔性并联机器人,如Kang D等人[1]以光学精密定位为背景研制了一种新型的大行程柔性铰链并联机器人,该六自由度的机器人工作空间±2mm*±2mm *±2mm *±2°*±2°*±2°,移动分辨率达到15nm,转动分辨率为0.14arcsec。Tang等人[6]设计并测试了具有XYZ3个自由度的柔性并联机器人,3个方向的运动相互解耦,行程达到2.3mm。经过测试,其横轴误差小于1.9%,移动引起转角小于1.5mrad。
以光学元器件的精密定位为应用背景,研究大行程柔性铰链Hexapod机构参数优化设计方法。柔性铰链的性能很大程度上决定了大行程柔性铰链Hexapod机构的性能。同样构型的柔性铰链,行程越大其离轴刚度越低,从而导致大行程全柔性铰链Hexapod机构整体的静刚度和精度下降。以满足动平台工作空间要求前提下柔性铰链的变形量最小为优化目标,优化设计大行程全柔性铰链Hexapod机构的结构参数。
1 运动学逆解
1.1 参数设定
为了简化研究,建立柔性铰链Hexapod机构的伪刚体模型。将支杆与动平台之间的柔性铰链假设为带转动刚度的球铰,支杆与动平台之间的柔性铰链假设为带转动刚度的万向铰,移动关节包括直线致动器与柔性直线导向机构。简化Hexapod机构如图1所示。上方的平台为动平台,下方的平台为定平台。为了方便分析,按图1所示建立定平台上的坐标系A(X,Y,Z)、动平台上的坐标系B(U,V,W)及分别对各支链i建立用DH方法建立坐标系(ri-j,si-j,ti-j),其 中,j=0,1,2…6。 坐 标 系(ri-0,si-0,ti-0)与坐标系(ri-6,si-6,ti-6)分别与坐标系A,B 相对固定,ti-0方向为初始状态下ri-0与Z轴叉乘乘积方向:
支链i的DH参数如表1所示。
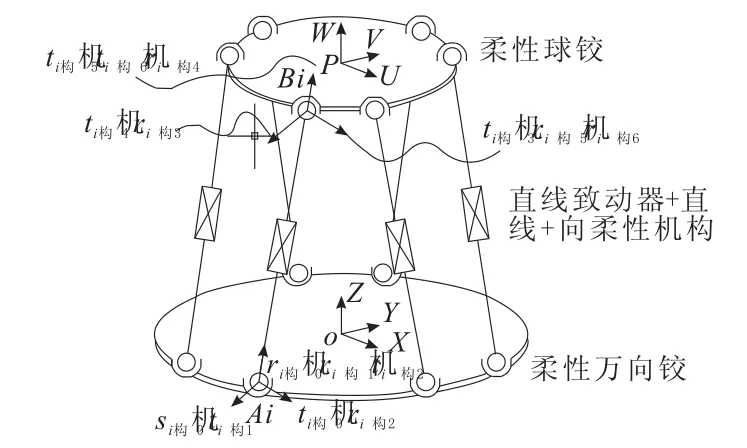
图1 伪刚体模型及坐标系

表1 支链DH参数
l为连杆两端关节运动副轴线之间的公垂线长度;α为连杆两端的关节轴线在该连杆长度的法平面内投影的夹角;d为相邻连杆的距离;θ为相邻连杆的夹角。
初始状态时各关节参数为[0°,-90°,di0,-90°,-90°,0°],di0为初始状态的支链长度。代入DH矩阵的计算公式,分别计算得到各连杆的齐次变换矩阵kAil(支链i中l坐标系在k坐标系中的表示)。
1.2 求解柔性铰链转角
求解关节转角的过程类似于六自由度的串联型机械臂求逆解的过程。将k中的旋转阵用k表示,AAB表示动平台相对于定平台的齐次变换矩阵。i支链杆长方向与ti-2方向相同:

考虑到θi-2的初始位置姿态值为-90°且柔性机器人关节转角均较小。因此,有-π≤θi-2≤0。可以求得:
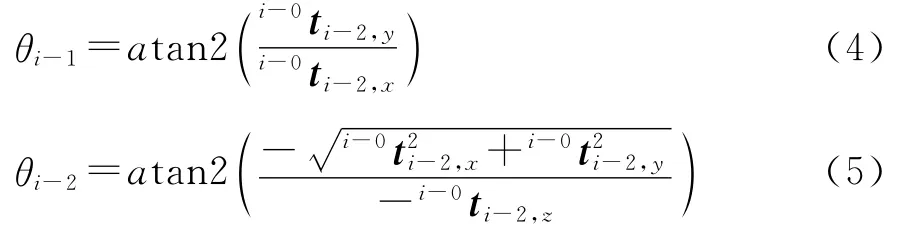
与动平台相对固定的向量ti-6在坐标系B中表示为Bti-6,下式中Bi0表示初始位置姿态时点Bi在A坐标系的坐标。
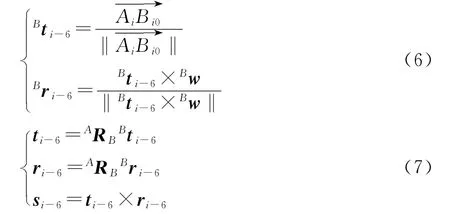
可以用上面的结果表示支链i整体的旋转矩阵A=[ri-6,si-6,ti-6]。
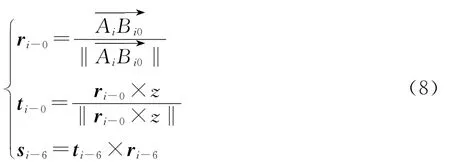
由上式可以得到0=[ri-0,si-0,ti-0],即可求得6。同时也由各个关节的旋转矩阵计算支链i整体的旋转矩阵为:
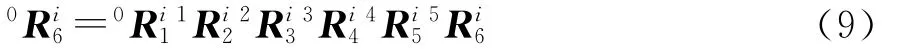
0可由θi-1,θi-2求得。将已知的旋转阵移至上述等式的左侧得:
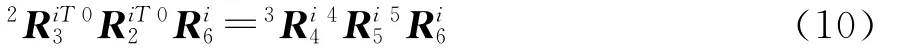
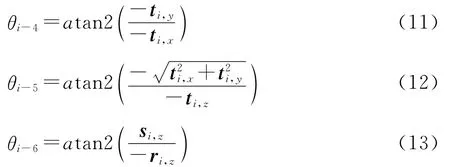
求解时考虑到θi-5的初始位置姿态值为-90°,柔性机器人关节转角均较小,取-π≤θi-5≤0。
至此,支链i的各关节运动量均已求得,可以得到相对于初始位置各关节转动的角度或移动量为:
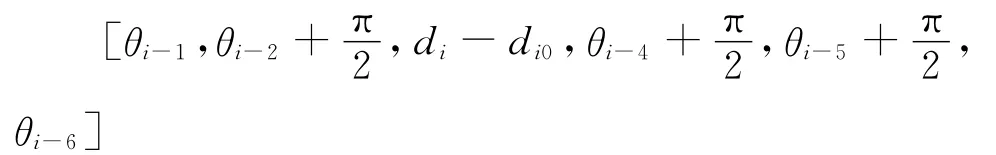
2 Hexapod参数优化
2.1 设计参数与要求
为了方便探讨,选取初始位置下对称的Hexapod类型,Hexapod机构的俯视图及参数定义如图2所示,图中的坐标系为定平台的坐标系A(x,y,z)。定义定平台上所有Ai所在的圆的半径为R,动平台上所有Bi所在圆的半径为r,A1与中心点O连线与Y轴的夹角为α,B5与中心点O连线与Y轴的夹角为β,初始状态下动平台与定平台的距离为h。Ai,Bi在坐标系A 中的坐标分别是:Ai=(Rcosαi,Rsinαi,0);Bi0=(rcosβi,rsinβi,h)
Bi0为初始位置姿态时Bi点在A 坐标系的坐标。具体的αi,βi,分别用α,β表示为:

设计时考虑到相邻的Ai及相邻的Bi不会重复或者交叉,限定10°≤α≤50°,10°≤β≤50°。考虑到实际的应用背景和结构的紧凑性,限定与动平台相连的柔性球铰中心所在圆的半径100mm≤r≤200 mm,与定平台相连的柔性万向铰中心所在圆的半径150mm≤R≤250mm,初始状态下定平台与动平台之间的高度150mm≤h≤250mm。后面的优化设计将在上述的范围内对参数R,r,h,α,β优化设计,以获取在满足工作空间要求情况下使得所有柔性铰链的变形范围中的最大值最小的一组参数。Hexapod动平台沿X,Y,Z轴移动的范围均为±5 mm,绕X,Y轴旋转的角度范围为±2°,绕Z轴旋转范围不作要求。
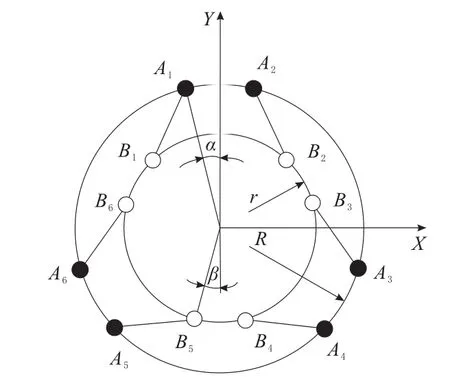
图2 Hexapod参数定义
2.2 平台参数优化计算
设计时取初始条件下各柔性铰链的变形值为零,根据要求的工作空间得到动平台的位置与姿态六维向量xp=[px,py,pz,φx,φy,φz]的取值范围。
对于给定的任意平台参数,使动平台在某一个轴向移动或转动到极限位置。按照第1节推导的表达式计算柔性铰链的转角,从中计算得每个支链的5个角度逆解,即30个角度逆解值中的最大绝对值与最大移动绝对值加权求和。依次求取每个轴向2个极限位置即10个极限位置(绕Z轴的旋转由于光学镜面的定位中没有要求故不予考虑,每个轴移动或转动方向分别取正负最大值)的加权和,选择其中最大的作为此平台参数下需要的柔性铰链变形量的表征,选择使得该加权和最小的平台参数,即为最优化的平台参数。
编写Matlab程序寻求最优化的Hexapod机构参数基本的编程思路如下。
a.编写求运动学逆解的函数inverseKinematics。函数的输入为平台参数(r,R,h,α,β)及动平台的位置与姿态六维向量xp=[px,py,pz,φx,φy,φz],输出为所有6个支链每个支链5个转角逆解一个移动逆解,为6×6矩阵。
b.编写求柔性铰链最大转角绝对与最大移动绝对值的函数findMaxDisplacement。函数的输入为平台参数(r,R,h,α,β)及动平台的位置与姿态六维向量xp=[px,py,pz,φx,φy,φz],函数的输出为对应于该平台参数及位姿条件的30个柔性铰链变形值中的最大绝对值及6个直线导向的柔性铰链的变形值中的最大绝对值组成的向量。
c.编写满足工作空间要求的柔性铰链最大加权和计算函数maxDisplacement。函数的输入为平台参数(r,R,h,α,β),函数的输出为最大转角绝对值与最大移动绝对值加权和。利用函数findMaxDisplacement求取各轴向极限位置时的柔性铰链最大转动值,从得到的10个值中选取最大值作为输出。
d.将问题变为最优化问题。目标函数min maxDisplacement(r,R,h,α,β)限制条件为:
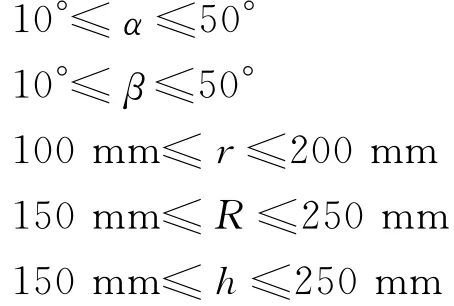
用Matlab工具箱中的最优化函数fmincon寻找限定条件下的最优化解,将算法设置为“interiorpoint”。设置不同的权重,得到局部最优解的情况如表2所示。
从表2中可以看出,按照优化时对最大转角绝对值和最大移动绝对值分配权重的不同可以将Stewart平台的设计参数分为3类:第1类使得转动导向的柔性铰链需求的运动范围最小;第2类使得直线导向的柔性铰链需求的运动范围最小;第3类综合最优,使得整个平台柔性教练的转动角度和伸缩量都取得比较小的数值,但均不是最小值。设计时可以按照综合最优选取平台参数,也可以按照某种铰链的运动范围要求最小进行设计。
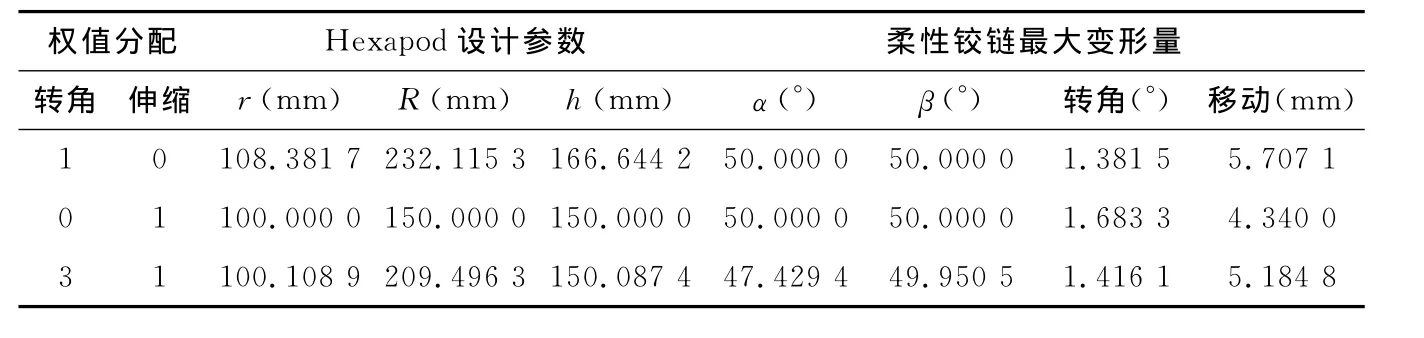
表2 Hexapod优化设计参数
3 结束语
以柔性铰链的要求变形值最小为优化目标,在满足大行程柔性Hexapod机构工作空间要求的前提下进行Hexapod机构参数的优化设计。建立了大行程柔性Hexapod的伪刚体模型的各支链坐标系,求取了各支链各关节运动学逆解的解析表达式,并以此为基础进行了Hexapod机构的优化设计。从最后优化设计实例的计算中可以看出,实际设计时,可以以某种柔性铰链的变形量要求最小或两种变形的加权和最小为设计目标优化设计Hexapod机构的参数,也可以根据设计完成的两种柔性铰链能够满足整体的行程范围要求,调整各自的权值使其满足要求从而进行Stewart平台的参数配置。
[1] Kang D,Gweon D.Development of flexure based 6-degrees of freedom parallel nano-positioning system with large displacement[J].Review of Scientific Instruments,2012,83(3):035003-035009.
[2] Budinoff J G,Michels G J.Design and optimization of the spherical primary optical telescope(SPOT)primary mirror segment[A].Optics &Photonics 2005International Society for Optics and Photonics[C].2005.356-361.
[3] Ellis G W.Piezoelectric micromanipulators[J].Science Instruments and Techniques,1962,(138):84-91.
[4] Grace K W,Colgate J E,Glucksberg M R,et al.A six degree of freedom micromanipulator for ophthalmic surgery[A].1993IEEE International Conference on Robotics and Automation[C].1993.630-635.
[5] 王振华,陈立国,孙立宁.集成式6自由度微动并联机器人系统[J].光学精密工程,2007,15(9):1391-1397.
[6] Tang X,Chen I M.A large-displacement 3-DOF flexure parallel mechanism with decoupled kinematics struc-ture[A].2006IEEE/RSJ International Conference on Intelligent Robots and Systems[C].2006.1668-1673.

