机械系统静态特性的有限元耦合分析研究
刘 洁
(延安大学化学与化工学院,陕西 延安716000)
0 引言
商用有限元软件是一个黑盒子,其二次开发只能做一些外围工作,其核心接触算法属于商业秘密。现在需要修改接触算法及其收敛条件,才能引入结合面的特性参数进行耦合分析,并且需要设计新的算法才能求解整机。基于有限元法,研究重点是把接触算法和结合部理论进行融合,设计耦合求解算法,并编制耦合分析软件,最后用实验进行验证。
1 有限元耦合分析
1.1 建立接触系统的求解方程
设机械系统Ⅰ与机械系统Ⅱ相互接触,每个机械系统可以是单个零件,也可以是由许多零部件通过柔性结合部连接成的装配体[1]。建立机械系统Ⅰ与Ⅱ的离散平衡方程式(1)和(2),并对其系数刚度矩阵进行分块,然后引入已知位移和力边界条件。
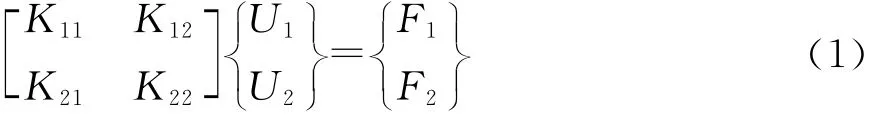
U1为系统Ⅰ非接触边界节点的位移列阵;U2为系统Ⅰ接触边界节点的位移列阵;F1为系统Ⅰ非接触边界节点的力边界条件列阵;F2为系统Ⅰ接触边界节点的接触力列阵。
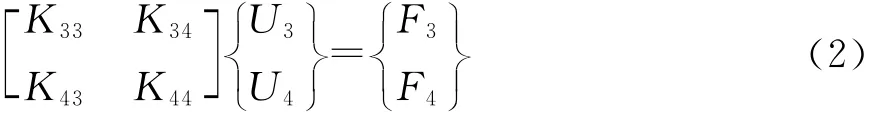
U3为系统Ⅱ接触边界节点的位移列阵;U4为系统Ⅱ非接触边界节点的位移列阵;F3为系统Ⅱ接触边界节点的力边界条件列阵;F4为系统Ⅱ非接触边界节点的接触力列阵。
接触力满足F2=-F3,但是接触力的大小是未知的,所以方程无法直接求解。
1.2 结合部子结构的罚函数法有限元
将接触区域的非嵌入条件以及其他附加条件作为惩罚项引入接触域子结构的泛函中,将接触问题转化为关于接触刚度的优化问题[2-4]。接触刚度的物理意义是结合面抵抗变形的能力,相当于在接触点对之间嵌入1个法向、2个切向压缩弹簧,来抵抗节点间法向和切向的相对位移。
由式(1)和式(2)经过静力凝聚消去U1,U4后得到:
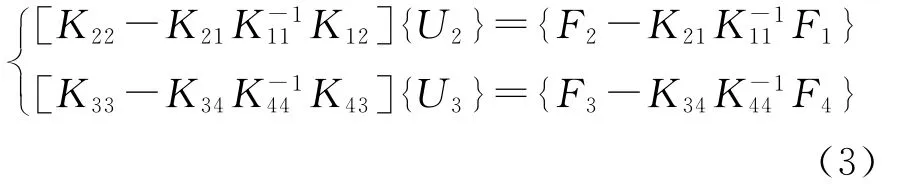
建立结合部子结构的泛函:
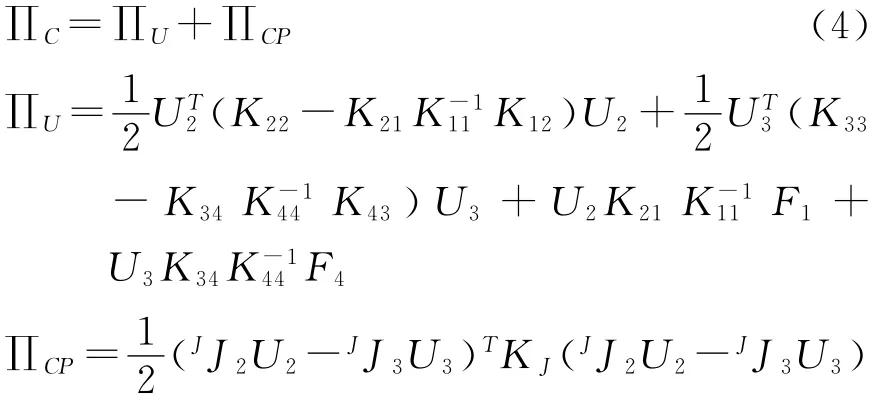
∏U为接触域子结构不包括接触条件的总势能;∏CP为用罚函数法引入接触约束条件的附加泛函;KJ为接触刚度;JJ2,JJ3为总体坐标系与结合部局部坐标系之间的坐标变换矩阵。
根据最小势能原理,在满足边界条件的可能位移中,真实位移满足非嵌入条件,并使系统总势能取得极小值[5]。也就是接触的最终状态由系统平衡方程、力和位移边界条件以及接触域边界的非嵌入条件所惟一确定。
当泛函∏C取极值时,即

得到:
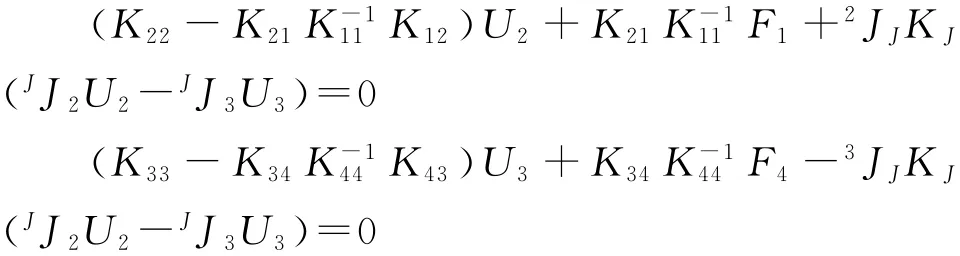
整理合并后得到接触域子结构的控制方程为:
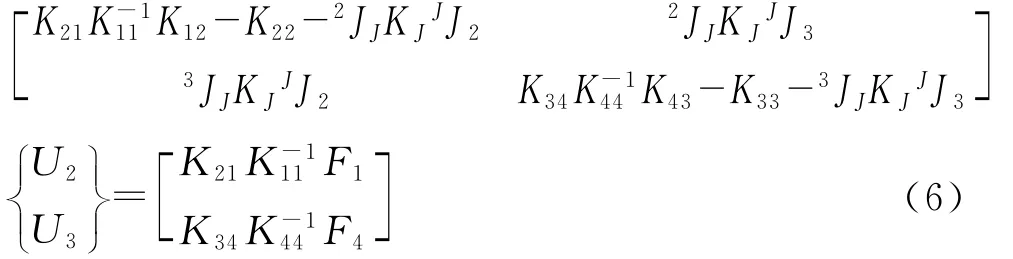
由罚函数法得到的显式方程式(6),可以采用基于载荷增量迭代的中心差分法求解。选用足够大等间距的罚因子数列δ1,δ2,δ3,…,δn,对于某个给定的δk,当接触表面层的最大相对位移量λ2max≤ε(ε为给定的最大相对位移量)时,认为迭代收敛。
罚函数法的优点是算法简单,易于编程[6]。但接触条件只是近似被满足,在接触域存在穿透,最大相对位移量由给定的常量ε来控制。当选用的罚因子δk过大时,此时的接触刚度会很大,从而引起计算结果的病态。
1.3 对接触域的精确处理
如果对计算精度的要求比较高时,需要检验罚函数法的计算结果是否合理,并做进一步精确处理。
设第k个接触点对之间由接触表面层变形产生的法向位移为λ2k,切向相对位移为λ1k,λ3k,则
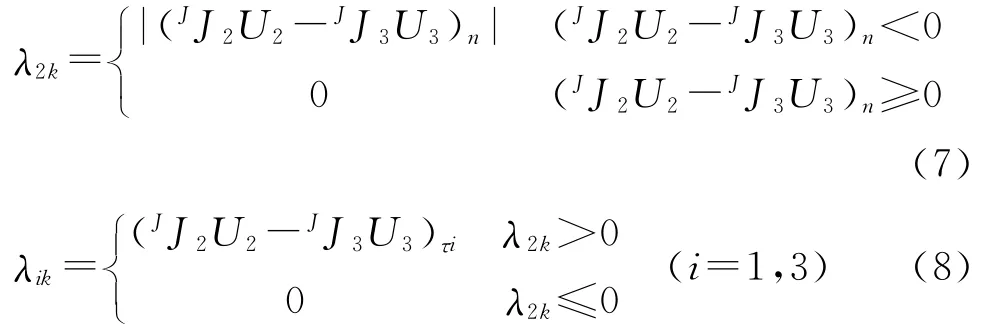
合并写成列阵得到:

则第k个接触点对之间的接触面压为:

将非线性接触面压等效为节点载荷得:
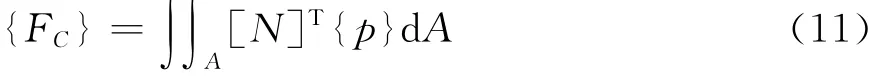
[N]为单元形函数矩阵。
将结合部的相对变形{λk}和接触力{FC}进行集成装配,得到总的列阵{λ}和{FC}。

联立式(6)和式(12),使用增量迭代法求解,最终让接触表面层的最大相对位移量等于接触表面层的相对变形。当满足收敛条件后,由式(12)得到接触节点的接触力FC列阵,将FC带入式(1)和式(2)即可求解机械系统Ⅰ与Ⅱ。
一般情况下,机械系统Ⅰ没有足够的位移边界条件,其刚度矩阵具有奇异性。还需要在机械系统Ⅰ上引入一个位移约束,并推出此时的刚体位移公式和由此产生的整体附加平衡条件,与式(1)联立求解。
机械系统Ⅰ和Ⅱ都应满足整体附加平衡条件:
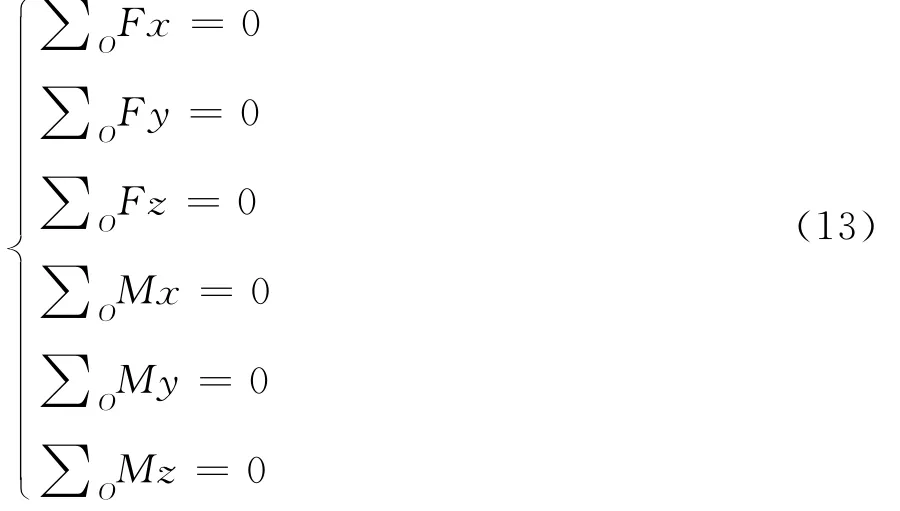
因结合部相对位移的数量级一般小于等于微米级,而接触区域的零件宏观变形和本体结构及外载荷相关,进行耦合时有以下2种迭代方案。
a.实时处理。当接触区域的零件宏观变形和结合部的相对变形处于同一个数量级(或者相差较小)时,则在每一次迭代过程中均代入结合面的基础特性参数,对接触域进行实时修正。
b.最终处理。当接触区域的零件宏观变形和结合部的相对变形相差几个数量级时,先不代入结合面的基础特性参数,即先用罚函数法求出大致的接触域后,再代入结合面的基础特性参数做准确处理,对接触域进行精确的修正。
2 误差分析
误差分析也是有限元计算中的重要问题之一,在计算过程中需要估计误差,如果误差过大,则需要改用高阶单元,或者增加局部的单元密度,来保证计算精度。
2.1 计算误差
2.1.1 舍入误差
由于计算机字长所限,需要对原始数据、中间结果和最终结果保留有限位数字,有限位小数后的尾数部分做四舍五入处理,这种由四舍五入产生的误差被称为舍入误差。舍入误差是不可避免的,而且对整体计算精度的影响非常小。
2.1.2 截断误差
由于实际运算只能完成有限项或有限步运算,对无穷过程进行截断,这样产生的误差成为截断误差。例如,求一个级数的和或无穷序列的极限时,取有限项作为它们的近似,从而产生了截断误差。
2.1.3 其他计算误差
由计算格式、迭代格式、运算方式和运算次数等的不同引起的误差。在运算过程中,应尽量减少迭代次数,计算次数的增加,会使误差得到累积和传播。
2.2 模型误差
2.2.1 单元离散误差
由离散单元的几何形状产生的误差,以直边代替曲边、以平面代替曲面。使有限元结果和理论结果之间存在误差,当离散的单元个数越多,计算精度就越高。但离散的单元个数越多,计算量就越大。
在求解整机时,处理接触问题是计算的核心,则需要增加接触域的单元密度,来提高接触域的计算精度。必要时,还需要在迭代过程中,对接触域的局部重新自适应划分网格,来提高局部的计算精度。
2.2.2 形函数误差
形函数误差是由位移模式的阶次低于实际形函数多项式的阶次而产生的。如果不满足形函数的收敛准则,其误差不会因单元数目的增多和网格的细化而消失。

N为单元形函数;δe为已求解出的节点位移。
则其误差为:

整个结构的能量误差模型为:
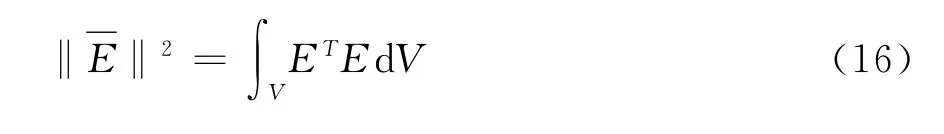
3 实验验证及分析
3.1 实验装置
实验装置如图1所示,共用8个位移传感器检测变形及1个压电陶瓷力传感器检测螺栓预紧力。预紧力分为10次递增施加,每次2 000N。然后分10次递减卸载,再次检测其变形。当预紧力较小时,加载过程平稳,比较准确。但预紧力较大时,螺纹间的摩擦力增大,加载过程有振动,不容易控制载荷的大小。经过多次实验发现,2 000N,4 000N和6 000N的试验结果比较准确。

图1 实验装置
3.2 理论分析结果和实验结果的比较
在螺栓预紧力为2 000N和4 000N时,法向接触面压小于2.5MPa,零件本体的变形较小,接触表面层表现出明显的非线性特性。因此,对2 000 N和4 000N时的分析结果和实验结果进行比较。
通过实验发现,在预紧力为2 000N和4 000N时,小圆柱体上端面上大多数节点的位移都为负值,即小圆柱整体向下位移,与耦合分析的结果基本一致。
用传感器检测小圆柱体上端面上A,B和C3个点的位移,然后和理论分析结果进行比较,如图2所示。
当预紧力从2 000 N增加到4 000N时,主要比较A,B和C 3个点的位移增量值,如表1所示。经过多次实验检测,取其平均值。
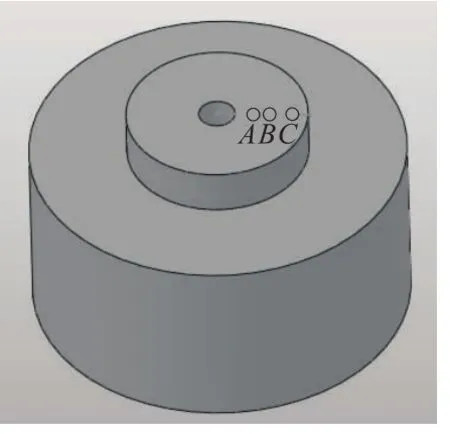
图2 测量点的位置
从表1可以看出,耦合分析结果和实验测量结果非常接近,即零件的变形趋势大致相同,但在数值上有一定的误差。其原因有以下几点:
a.由于磨削加工方法和加工精度的不同,零件的表面完整性会有差异。在相互配对构成结合面时,纹理方向的不同也会影响实验结果。因此,结合面的基础特性参数和零件真实的接触特性之间存在误差。没有考虑接触域的真实微观形状,按照理论设计尺寸建立有限元模型,算法依赖于结合面的基础特性参数,分析结果是一个预测值。因此,和实验测量值之间存在误差。
b.结合面的基础特性参数基于单位面积,但在加工后零件存在形位误差,且尺寸越大,误差就越大。建立有限元模型时,也没有考虑零件的形位误差。因此,理论分析和实验测量值之间存在误差。
c.在实验时,由于仪器的测量精度有限,而且测量的准确性也依赖于实验装置是否可靠性,以及测量水平的高低。因此,测量结果可能会不准确。

表1 耦合分析结果与实验测量结果
4 结束语
将接触表面层的接触面压与接触变形非线性关系,代入到接触问题的控制方程中,最终让接触域的穿透量等于接触表面层的相对位移。并讨论了实时耦合处理和最终耦合处理两种方法及其适用场合。并且从计算误差和模型误差两个方面分析了有限元法的误差。最后用一个实例对耦合分析软件进行测试,并用实验进行了多次检测,验证了耦合分析结果与实验结果基本一致。因此,提出的机械系统有限元耦合分析算法是正确的。
[1] 黄玉美,张广鹏,高 峰.虚拟样机整机结构特性边界元仿真[M].北京:机械工业出版社,2004.
[2] 董献国.导轨结合部的变形解析、加工误差综合及其结构优化设计[D].西安:陕西机械学院,1989.
[3] 王晓春,孔祥安.接触力学及其计算方法[J].西南交通大学学报,1996,31(3):230-233.
[4] 温卫东,高德平.接触问题数值分析方法的研究现状与发展[J].南京航空航天大学学报,1994,26(5):664-667.
[5] 刘晓平,徐燕申,宋健伟,等.机械结构结合面阻尼特征参数识别的研究[J].振动与冲击,1995,14(3):61-65.
[6] Ohtakake K,Oden J T,Kikuchi N.Analysis of certain unilateral problem in von karman plate theory by a Penalty method-Part I:a variational primciple with penalty[J].Computer & Methods in Applied Mechan-ics and Engineering,1980,24(2):187-213.

