黏土地基近海风机桶形基础累积变形研究

邢占清，高季章，张金接，符 平

（中国水利水电科学研究院 北京中水科水电科技开发有限公司，北京 100038）

黏土地基近海风机桶形基础累积变形研究

邢占清，高季章，张金接，符 平

（中国水利水电科学研究院 北京中水科水电科技开发有限公司，北京 100038）

基于黏土循环累积变形的半经验公式，将土体循环累积变形等效为蠕变，形成了近海风机桶形基础累积变形的有限元计算方法。在长期实测响水近海海域风、浪数据的基础上，以已建2 MW风机参数进行分析，得到了不同循环作用次数下桶形基础中心沉降量、不均匀沉降量和倾斜率。计算结果表明，风机运行期内桶形基础变形可满足风机运行要求。

近海风机；桶形基础；累积变形；循环荷载

1 研究背景

风力发电是目前技术最成熟、最具规模化开发条件和商业化发展前景的可再生能源发电方式之一。根据中国气象局风能资源详查成果，我国近海风电开发潜力巨大：5～25 m水深线以内近海区域、海平面以上70 m高度风电可装机容量约5亿kW［1-2］。东部沿海的经济发展和电网特点与欧洲类似，适于优先大规模发展海上风电，但该区域海床普遍分布有较厚的海洋性黏土（厚度通常大于10 m）［3］。与常用的桩基础相比，桶形基础安装简单、海上工期短、造价低，且一般不需进入物性较好的深部持力层，对深厚黏土地基适应性较好。

近年来许多学者围绕海上风机桶形基础的极限承载特性做了大量研究工作，如刘喜珠［4］对饱和粉砂土地基上的海上风机桶形基础破坏模式及安全性进行了研究；孙曦源［5］采用三维有限元分析方法就杭州湾近海风机桶形基础稳定性进行了研究，但针对风机运行期内桶形基础累积变形的研究并不多见。相对于其他海上构筑物而言，海上风机属高耸结构，基础承受的水平荷载和弯矩较大；风机运行对基础倾斜率要求较高，基础设计通常由变形控制。因此，研究长期风浪作用下黏土地基桶形基础累积变形具有重要意义。本文基于黏土循环累积变形的半经验公式，将土体循环累积变形等效为蠕变，形成了近海风机桶形基础累积变形的有限元计算方法，并根据响水近海海域长期实测风、浪数据，对风机运行期内桶形基础变形进行了预测研究。

2 风浪作用下黏土的变形特性

风浪等循环荷载作用下黏土会发生软化，变形具有明显的时效性，原因大致可以分为3类：（1）循环荷载作用下饱和黏土产生孔压；（2）循环荷载作用下主应力方向不断改变导致土体结构重塑；（3）较高的循环应力作用不仅产生较高的孔压，且影响土体的原有结构［6］。土体的循环累积变形是一个复杂的过程，目前主要有两种研究思路［6-9］：（1）详细跟踪每一次动荷载作用过程，建立相应的动应力-动应变关系，从而求得土体的累积变形，该法计算量大，对于循环次数几千次以上的情况，可能会造成较大的计算累积误差，有时计算收敛性也是一个难以克服的问题；（2）只考虑每一次循环后的累积变形，通过建立循环累积应变关系式计算土体累积变形。研究风浪长期作用下桶形基础变形特性时，需考虑的作用时间长、循环次数多，本文基于第（2）种思路进行研究。

循环累积变形特性不仅与土体的物性指标、固结状态有关，且与静荷载、循环荷载、循环振次有密切的关系。当土的物性指标、固结状态确定后，影响土体变形特性的主要因素有3个方面：（1）循环荷载作用前土体单元初始应力状态；（2）循环荷载的大小及作用方式；（3）循环荷载作用次数。

Monismith［8］于1975年提出了循环荷载作用下黏土累积变形的指数模型，如下式：

式中：εp为累积塑性应变；A和b为常数；N为循环荷载的作用次数。

考虑动应力的影响，Li等［9］于1996年对式（1）常数A进行了修正，如下式：

式中：a和m为常数，并给出了不同土体的参数建议值，见表1；qd为动应力幅值、qf为土体静强度。

考虑土体初始静应力的影响，Jin-Chun Chai等［10］于2002年对式（2）进行了发展，如下式：

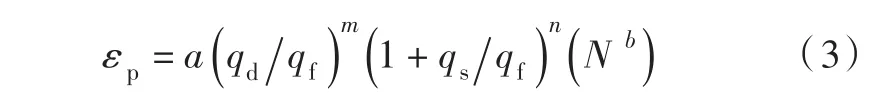
式中：qs为土体初始静应力，n为常数；建议常数 a、b、m仍按表1取值，常数n取1，并给出了多个黏土变形计算值与实测值较为吻合的案例。本文基于式（3）开展研究。

表1 Li和Selig提出的不同土体参数建议值

3 桶形基础累积变形分析模型

3.1 计算方法与步骤风机运行期间桶形基础受结构自重和风浪引起荷载的共同作用，其中自重和平均风压引起的荷载将较长时间保持不变，地基土单元产生大小不同的静应力qs；脉动风压和波浪产生的荷载通过基础传至地基土体中，又使土单元受到了随时间而变化的循环应力作用，不同土单元动应力的幅值为qd。土单元的累积应变随着循环次数的增加而增加，循环次数可看作是时间过程，将循环累积应变增量等效为蠕变增量，土单元的应变增量可分为弹性应变增量dεe、塑性应变增量dεp和蠕变应变增量dεc，即dε=dεe+dεp+dεc。因而，可通过增量弹塑性有限元计算，确定地基土单元的静应力qs、动应力幅值qd，进而利用式（3）计算蠕变应变增量dεc，再通过增量弹塑性有限元计算，就可以求得桶形基础受到静荷载和经过一定循环次数共同作用的累积变形。

为了计算蠕变应变增量dεc，本文对ANSYS有限元软件进行了二次开发：将式（3）写成自定义蠕变子程序，并定义了一个确定土体动应力的场变量，与ANSYS主程序进行重新编译链接后进行计算。具体分析步骤如下。

（1）建立有限元分析模型，施加静荷载，计算结束后输出土单元的应力，并根据式（4）计算各单元广义剪应力q，将其作为初始静应力qs；

（2）在施加静荷载的基础上施加循环荷载幅值，输出土体各单元的应力并利用式（4）计算广义剪应力，记为qj+d；

（3）根据式（5）计算各土单元动应力幅值qd；

（4）在第（1）步的基础上，将各土单元动应力qd写入单元场变量，重新进行计算。

3.2 计算方法验证ANSYS二次开发后对蠕变量的计算进行了验证。模型高、宽均为1 m，长10 m；左侧施加固定约束，右侧5 m范围内除右端面外的表面施加面荷载，如图1所示。蠕应变理论值与ANSYS计算值对比结果见表2，由表2可以看出二者相差较小，模型开发合理。

图1 验证模型

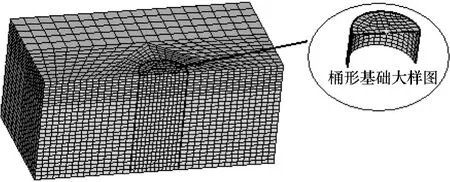
图2 分析模型

表2 模型蠕变应变量验证结果

4 典型海域条件下桶形基础变形研究

4.1 分析模型响水2 MW试验风机离岸约3.5 km，水深约4 m，海床以下19 m深度内以黏土为主，本文以该案例参数进行分析，土体采用mises屈服准则［13］。假定风、浪长期作用方向一致，桶形基础及土体受到的荷载轴对称，建立轴对称模型进行分析，如图2所示。土体中心轴面施加对称约束，除中心轴面外的侧面施加垂直于侧面的位移约束，底面施加竖向约束；桶体中心轴处施加对称约束。桶土间采用接触摩擦，摩擦系数取0.32［14］，其他参数取值见表3。

表3 分析模型参数取值

4.2 实测风浪距响水近海试验风机约5 km处设有1座70 m高的海上测风塔，测风塔附近设有波浪观测设备。试验风机额定风速为10.8 m/s，切出风速为 25.0 m/s。风机满发运行对基础影响最大，对2008年7月—2009年6月 70 m高度 10.8～25.0 m/s范围内的风速进行分析。从长期统计结果来看，10 min最大风速vmax、10 min平均风速vavg间差值与 10 min平均风速vavg、10 min最小风速vmin基本相当，将作为脉动风速比例，不同风速下脉动风速比例间关系见图3，不同风速下脉动风速比例年内均值约为20%，由此可得到不同风速条件下的vmin、vmax的长期统计值。将vavg对应风压作为静风压，将vmin、vmax对应风压与静风压间差值的均值作为长期脉动风压，具体见表4。

对同期波浪观测数据进行了统计，波浪参数与70 m高度10 min平均风速间关系见图4—图6，分析时长期条件下波浪参数取值见表5。

图3 70 m高度10 min平均风速与脉动风速关系

表4 70 m高度处风速和风压对照

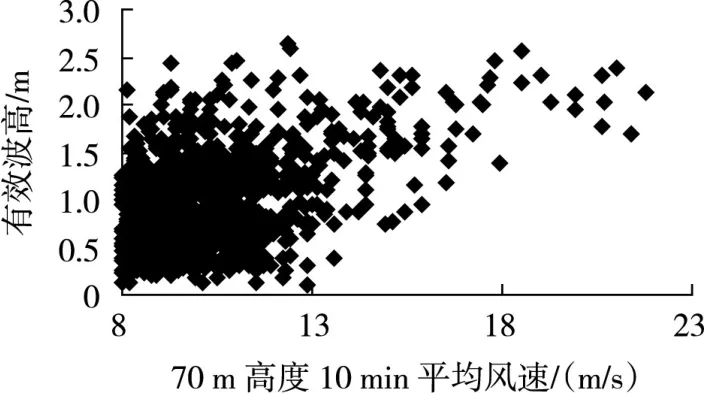
图4 有效波高与70 m高度10 min平均风速关系

图5 最大波高与70 m高度10 min平均风速关系

图6 有效周期与70 m高度10 min平均风速关系

表5 70 m高度10 min平均风速与同时段波浪参数

4.3 计算荷载塔筒和风轮为主要受风部件，塔筒承受的风压随高度变化，可由70 m高度的风压和《建筑结构荷载规范》（GB 50009-2012）规定的风压高度变化系数求得，塔筒直径与风压乘积沿塔筒积分求得塔筒承受的风荷载；风轮承受的风荷载可由70 m高度的风压、风轮直径和风机厂家推荐的水平推力系数近似求得，其中响水试验风机水平推力系数见表6。根据《海港水文规范》（JTJ 213-98）莫力森公式求得波浪荷载。竖向荷载仅为重力荷载。重力荷载和平均风压引起的荷载作为静荷载，脉动风压和波浪引起的荷载作为动荷载峰值，推求的作用在桶形基础顶端的荷载见表7。可以看出，10.8 m/s风速条件下力矩最大，25.0 m/s风速条件下水平力最大，故选取10.8 m/s、25.0 m/s风速条件下的荷载进行分析。

4.4 分析结果图7—图9给出了桶顶中心竖向位移、

桶基不均匀沉降和倾斜率随循环次数的变化关系。可以看出，中心竖向位移、不均匀沉降和倾斜率与循环次数大致呈对数关系；桶基中心点发生了竖直向上的负沉降，经108次循环后竖向位移最大增量为0.039 m；桶基发生了倾斜，经108次循环后最大不均沉降量为0.135 m，最大倾斜率为0.449%。根据《风电机组地基基础设计规定》（FD 003-2007），轮毂高度70 m、高压缩性黏性土条件下基础沉降允许值为0.2 m、倾斜率允许值为0.5%，桶形基础位移满足该规定要求。

表6 响水试验风机水平推力系数

表7 作用在桶形基础顶端的荷载

图7 桶基中心点沉降与循环次数关系

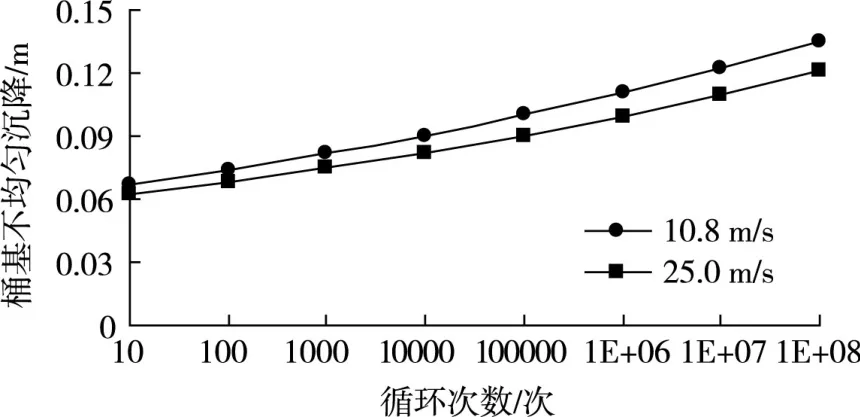
图8 桶基不均匀沉降与循环次数关系

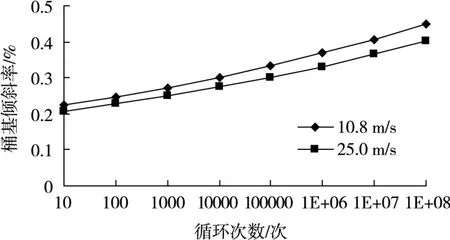
图9 桶基倾斜率与循环次数关系

实测波浪有效周期基本处于2～8 s范围之内；根据杨锋［15］采用Kaimal风速功率谱模型得到的本海域典型风荷载脉动时程曲线，考虑海上风况及风机结构特性，假定顺风向风脉动周期约为5 s。风浪联合作用周期按 5 s考虑，风速 10.8～25.0 m/s范围内 108次循环大致可代表风机满发 15.85年。根据可研报告，响水2 MW试验风机预估年满发小时数为2460，即等效满发时间约为28%。因此，保守估计50年内桶形基础累积变形不会对风机运行造成较大的影响。

5 结论

（1）基于黏土循环累积变形的半经验公式，将土体循环累积变形等效为蠕变，形成了近海风机桶形基础累积变形的有限元计算方法。（2）统计分析了响水近海风、浪实测资料，并以响水2 MW近海示范风机为例，对桶形基础累积变形进行了研究，得到了设计条件下风机运行50年桶基累积变形不会对风机运行造成较大的影响的结论。（3）计算模型以场变量的形式直接指定了土单元的动应力，计算过程中该值不随单元变形的发展而变化，这与实际情况存在一定的差别，有待进一步开展耦合研究。

参 考 文 献：

［1］ 我国风能开发潜力逾25×108kW［N］.人民日报，2010-01-05（10）.

［2］ 朱成章.关于中国风能资源储量的质疑［J］.中外能源，2010，15（4）：34-38.

［3］ 高国瑞.论中国区域性土的分布和岩土性质的形成［J］.岩土工程学报，2005，27（5）：511-515.

［4］ 刘喜珠.海上风电大直径宽浅筒型基础结构设计及安全性研究［D］.天津：天津大学，2010.

［5］ 孙曦源.水平荷载作用下软土地基中桶形基础工作机理及承载性能研究［D］.大连：大连理工大学，2009.

［6］ 周建，龚晓南.循环荷载作用下饱和软粘土应变软化研究［J］.土木工程学报，2000，33（5）：75-78.

［7］ 王建华，要明伦.软黏土不排水循环特性的弹塑性模拟［J］.岩土工程学报，1996，18（3）：11-18.

［8］ Monismith C L，Ogawa N，Freeme C R.Permanent deformation characteristics of subgrade soils due to repeated loading［J］.Transport Research Record，1975，537：1-17.

［9］ Li D，Selig E T.Cumulative plastic deformation for fine-grained subgrade soils［J］.Journal of Geotechnical Engi⁃neering，1996，122（12）：1006-1-13.

［10］ Jin-Chun Chai，Miura N.Traffic-load-induced permanent deformation of road on soft subsoil［J］.Journal of Geo⁃technical and Geoenvironmental Engineering，2002，128（11）：907-916.

［11］ 李建光，祁惠君 .地基土模量的取值方法及其在有限元计算中的应用［J］.工程勘察，2008（增刊2）：68-70.

［12］ 贾堤，石峰，郑刚，等.深基坑工程数值模拟土体弹性模量取值的探讨［J］.岩土工程学报，2008，30（增刊）：155-158.

［13］ 刘振纹，秦崇仁，王建华 .软黏土地基上循环承载力的计算模型研究［J］.岩土力学，2004，25（增刊）：405-408.

［14］ 张爱军，谢定义.复合地基三维数值分析［M］.北京：科学出版社，2004.

［15］ 杨锋，高季章，张金接，等.近海风机基础-塔架结构体系振动监测与动力响应分析［J］.中国水利水电科学研究院学报，2013，11（2）：87-93.

Accumulative deformation of offshore wind turbine bucket foundation in clay

XING Zhan-qing，GAO Ji-zhang，ZHANG Jin-jie，FU Ping
（China Institute of Water Resource and Hydropower Research，Beijing IWHR technology Co.，Ltd.，Beijing 100038，China）

Based on the semi-empirical relationship of clay accumulative deformation，taking cyclic cumula⁃tive deformation as creep，a finite element method for calculating accumulative deformation of offshore wind turbine bucket foundation in clay is developed.The long-term observation data of Xiangshui offshore wind and wave was Analysed.Taking 2 MW demonstration wind turbine as an example，an analysis model is es⁃tablished.Under different cycle number，the deformation of bucket foundation including central settlement，uneven settlement and gradient of slope，is studied by this method.The result shows that the deformation of bucket foundation still meet the requirements of wind turbine operation after 50 years.

offshore wind turbine；bucket foundation；accumulative deformation；repeated load

TU753

A

10.13244/j.cnki.jiwhr.2014.02.006

1672-3031（2014）02-0149-06

（责任编辑：李 琳）

2013-09-11

中国水利水电科学研究院科研专项（监1423）

邢占清（1981-），男，内蒙古卓资人，高级工程师，主要从事基础处理及海上风电方面的研究。E-mail：xingzhq@iwhr.com