透视投影下的月面撞击坑地形恢复算法研究
徐辛超,徐爱功,刘少创,徐宗秋
(1.辽宁工程技术大学测绘与地理科学学院,辽宁阜新 123000;2.中国科学院遥感应用研究所,北京 100101)
一、引 言
我国的探月工程是《国家中长期科学和技术发展规划纲要(2006—2020年)》中的16个重大专项之一,也是中华民族历史上重大的科技工程之一。2013年发射的嫦娥三号卫星将携带月面着陆器和月面巡视探测器实现月球软着陆和巡视探测任务[1]。由于月面巡视探测器在行进过程中可能会因地形判断错误陷入撞击坑或发生侧翻事故,为确保月面巡视探测器安全开展科学探测任务,首先需要以着陆区附近的三维地形为依据生成移动指令,完成巡视器的路径规划[2]。在着陆区中,作为月面最典型的地貌特征,撞击坑地形的出现是不可避免的,且该地形也容易导致侧翻事故的发生,因此,撞击坑地形的恢复具有非常重要的意义。
以摄影测量为基础的测图技术是测绘领域中获取地形的主要手段,即利用不同位置拍摄的影像,通过内外方位元素计算得到匹配点对的空间三维坐标,并最终由这些匹配点对实现地形恢复[3-4]。但在纹理缺乏、反射率单一的月表,只能得到较少量的匹配点,通过匹配点也只能得到精度较低的地形,不能满足巡视器路径规划的需求。SFS(shape from shading)是计算机视觉领域中的一种三维恢复技术,即通过影像中的各个像素灰度和物体表面反射模型为基础,建立反射方程,进而求解得到物体的三维形状[5]。SFS以影像像素为单位进行三维恢复,但由于SFS算法在恢复时要求物体表面的反射特性一致,因此其应用领域大大受到限制,并且现有关于SFS方面的算法较少,恢复精度有限。因此,研究一种适合月面撞击坑地形恢复的SFS算法可以为探月工程提供一定的技术保障。
二、透视投影下的SFS技术
SFS又被称为明暗恢复形状,主要用于计算机视觉领域。在地面影像中,由于地表物体反射率往往不一致,因此不能运用SFS技术进行恢复。但月球表面较为均匀的月壤成分为SFS技术的应用提供了基础。在传统SFS技术中,一般假设影像为正射投影,但在着陆器下降过程中获得的降落影像,由于相机焦距和角度不变,当着陆器高度较低时,影像的投影关系应视为透视投影,因此本文需要研究一种透视投影下的SFS技术。
1.传统SFS技术
运用SFS进行三维恢复时,要求物体表面的光照反射率已知,并且表面各点对应的光照反射率几乎一致,光源为已知位置的无穷远处的点光源;此外,影像拍摄过程可近似认为是正交投影[6]。在满足上述要求的基础上,按照一定的光照反射模型即可进行三维恢复[7]。
本文月面地形恢复过程中,采用探月一期处理影像时采用的反射模型——Lommel-Seeliger反射模型建立反射方程并求解[8]。图1为Lommel-Seeliger反射模型示意图,其中,e为观测者所在方向与物体表面法向量的夹角;i为光照入射角;L为光源方向;E为观察方向;N为物体表面法向量。
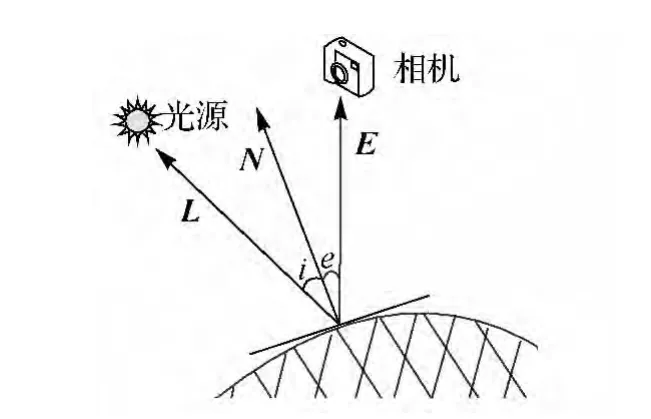
图1 Lommel-Seeliger反射模型
假设光源方向向量为N(ps,qs,-1),相机的方向向量为N(pe,qe,-1),物体表面点的法向量为N(nx,ny,nz)。为减少反射方程中的未知数,通常采用梯度形式的法向量N(p,q,-1)代替N(nx,ny,nz)。根据反射模型建立反射方程
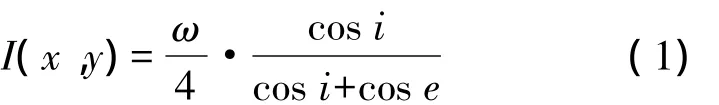
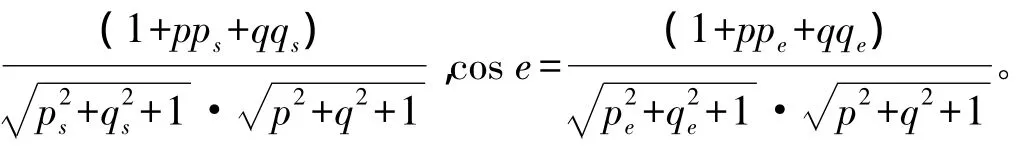
在反射方程中,p、q是未知的,但对于影像中的每个像素,只能建立一个方程。因此,SFS实际是个病态的问题,需要将其正则化后,通过方程的求解得到最终三维恢复结果。
2.透视投影下的SFS
当相机位置与月表距离较小时,影像的投影方式已经不能简单地近似为正射投影[9]。因此,需要研究透视投影情况下的SFS。
如图2所示,在像平面内的两条直线c1、c2分别平行于v轴和u轴,其在实际曲面S中对应的两条曲线分别为C1、C2。像平面内P点对应曲面S中的Q点。

图2 透视投影模型
将曲面方程写为参数形式后,可得透视投影下像平面内的曲线方程
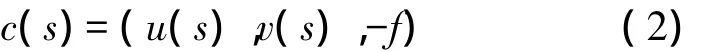
假设f为相机焦距,由透视投影与正射投影关系可得对应正射投影下的曲线方程
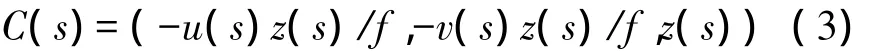
对应曲线C(s)的切线为
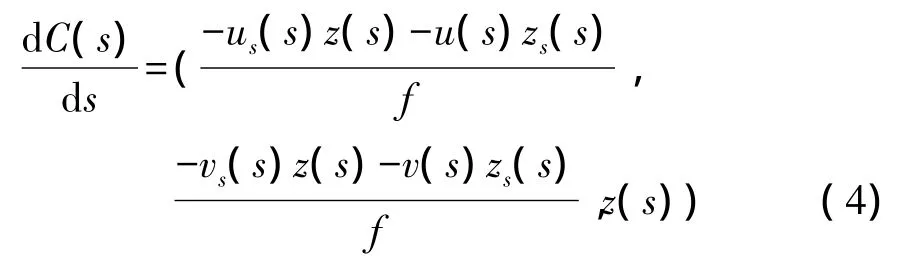
由于过点P的直线c1、c2平行于坐标轴且分别交坐标轴于v0和u0处,因此c1、c2可记为c1(u)、c2(v),实际曲面中对应的曲线方程记为C1(u)、C2(v),求取切线方程
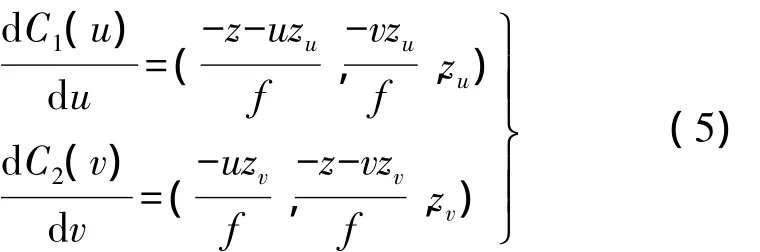
将二者叉乘即可得到实际曲面上点Q的法向量N,将其改写为梯度形式,即

由梯度定义可得p=zu/z,q=zv/z,以 Lommel-Seeliger反射模型建立透视投影下的反射方程,并整理得
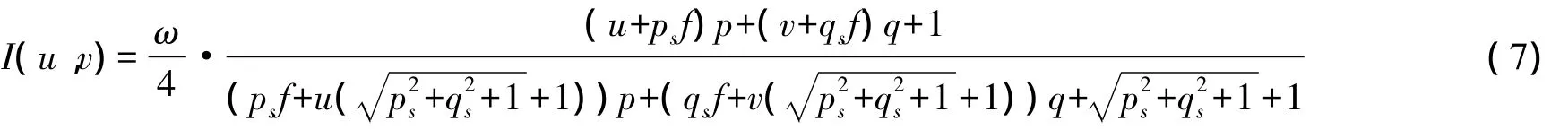
得到透视投影下的反射方程后,经过一定的约束求解过程,即可进行三维恢复。
三、透视投影下的撞击坑三维恢复
由于SFS建立的反射方程实际上是病态的方程,因此在建立透视投影下的反射方程后,需要增加一定的约束条件才能实现正确的三维恢复。
1.边缘线约束
边缘信息是影像中一个最基本的重要特征,在影像分析中起着重要的作用。边缘是指影像中局部特征突变的部分,在一定程度上反映出地形的特点。边缘线可以反映不同地形的变化,如撞击坑与周围地形的交界、斜坡面与月溪的交界等。
为方便问题描述,可以将撞击坑地形看做由垂直于其边缘线的宽度为ds的微小面块组成。如图3所示,建立OXYZ坐标系统,假设某边缘点处为原点O,沿着边缘线方向为Y轴方向,Z轴指向天顶方向,X轴和Y轴、Z轴构成右手空间直角坐标系。
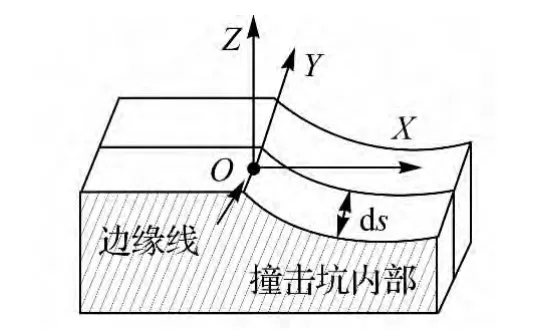
图3 OXYZ坐标系统
在与边缘线相邻的微小区域内,地形可近似看做是微小斜面,且该斜面过Y轴。假设其与XY平面夹角为α,其中0<α<90°,则该斜面方程在此坐标系下可以描述为

可得该区域内任意点(x,y,z)处的梯度形式法向量为(sin α/cos α,0,-0/cos α)。该向量在XY平面内的投影为(sin θ/cos θ,0),由此可得该区域内任意地形点的梯度比例k在XY平面内的投影为

即该微小斜面内的各点法向量在XY平面内的投影垂直于Y轴。
在OXYZ坐标下,其对应边缘线与Y轴重合,因此边缘线上的任意点法向量在XY平面内的投影也垂直于Y轴,即与边缘线相邻的微小斜面内各点的法向量在XY平面内的投影与边缘线点法向量在XY平面内的投影平行。因此,该微小斜面内的梯度比例即可由其附近边缘线的梯度比例求得。
2.连续性约束
一般情况下撞击坑内部地形表面都是连续的。为求取整个撞击坑内部其他点的梯度比例,本文算法在此运用了Horn提出的连续性约束条件。假设Ω为影像(x,y)的覆盖范围,连续地形表面模型可以表示为
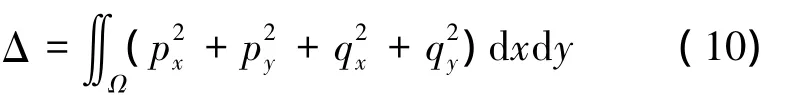
式中,px、py和qx、qy分别为p和q关于x、y方向的偏导数。
式(10)也可称为光滑约束条件,该条件下地形表面相邻各点的表面法向量是相似的。因此,相邻各点的梯度比例也是相似的。撞击坑内部除边缘线附近点外的其他点的梯度比例可按照连续性约束条件演化得到。
至此,根据本文提出的边缘线约束和连续性约束条件,即可运用撞击坑边缘线点法向量的梯度比例演化求得撞击坑内部任意点处的梯度比例k。将本文算法提出的梯度比例因子代入式(7),得到加入本文约束比例k后的反射方程为
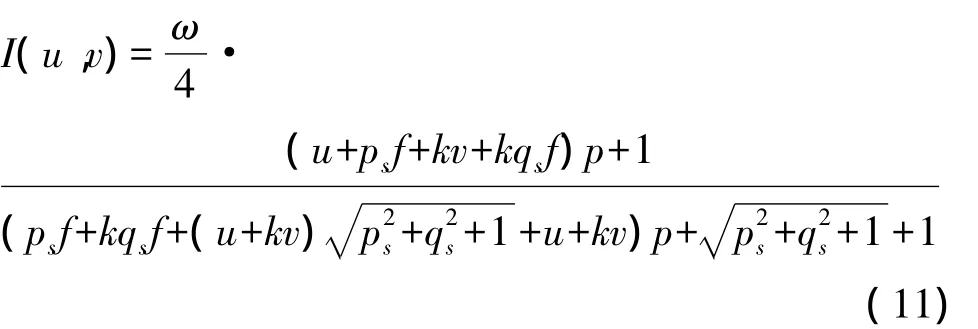
显然通过梯度比例与地形表面连续性约束后,本文算法在透视投影下的反射方程是正则化的,通过一定方法进行求解后,即可实现三维恢复。
四、试验分析
为了对本文提出算法的可行性进行论证,采用模拟影像进行了算法正确性测试,然后对月面影像进行了恢复测试,并与经典SFS方法进行了比较分析。
1.算法实现
由第三节得到的撞击坑的边缘线点处的梯度比例可求得整个撞击坑内部点的梯度比例,从而实现反射方程的约束,使得SFS问题能够正确求解。撞击坑地形恢复流程如图4所示。
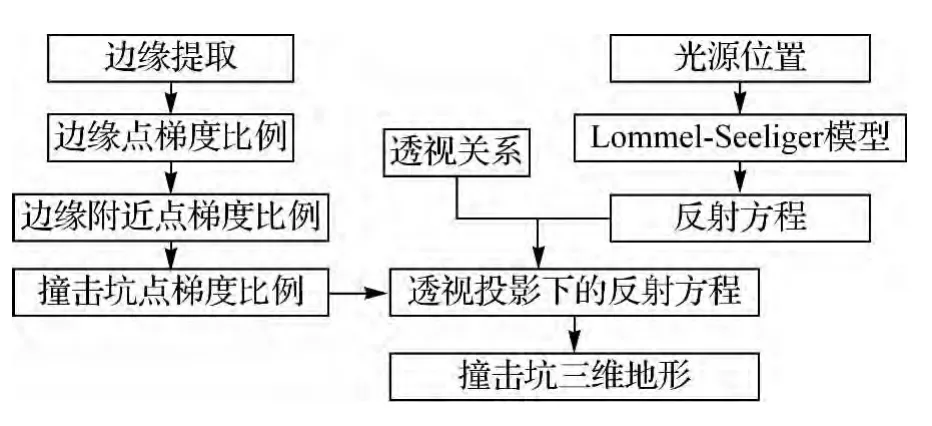
图4 透视投影下的撞击坑地形恢复流程
首先通过灰度卷积模板,得到撞击坑初步的边缘位置;然后对每个边缘像素周围的边缘点进行拟合,得到该边缘点处的梯度比例;此后按照曲面连续性约束条件,得到整个撞击坑的梯度比例;最后将得到的梯度比例代入透视投影下的反射方程,求解得到撞击坑的三维地形。
2.影像三维恢复
本文首先采用模拟影像对算法的可行性进行验证。图5为本文提出算法对模拟影像的恢复结果及恢复误差。模拟影像对应光照方向向量为(0.05,0.1,1)。

图5 模拟影像三维恢复结果及恢复误差
将图5中本文算法恢复结果与模拟影像真实值进行对比可以得出,本文算法的恢复结果与模拟影像结果非常接近,证明了本文算法的正确性和可行性,但仍存在一定程度的恢复误差。本文算法的平均误差为0.065,最大误差为0.157(由于SFS恢复结果为相对关系,在此只采用相对数值,无具体单位)。撞击坑内部点恢复误差较小,而误差较大的部分集中在撞击坑边缘附近。本文算法是基于地形特征边缘线的梯度约束展开,因此恢复误差的产生必然与特征边缘线有关。由于算法的局限性,根据灰度算子提取得到的特征边缘线与影像的实际边缘不可避免地存在位置偏差;此外,在梯度比例因子求取过程中还需要将特征边缘线进行拟合,在此过程中会产生拟合误差。因此,在真实边缘点与所提取得到的边缘点附近必然会存在较多的恢复误差。
本文采用真实月面影像对本文提出的算法及SFS算法中对真实野外影像恢复效果最好的Tsai算法进行了恢复效果测试,并得出了测试结果。真实月面影像中光照方向未知,因此在进行地形恢复时需要首先运用现有光照估计方法对光照方向进行估计。本文采用文献[11]中的方法进行估计,得到图6中月面撞击坑影像的光照方向分别为(1.0,1.2,1.5)和(-0.1,-1.2,1.5)。Tsai算法与本文算法的最终恢复效果如图6所示。
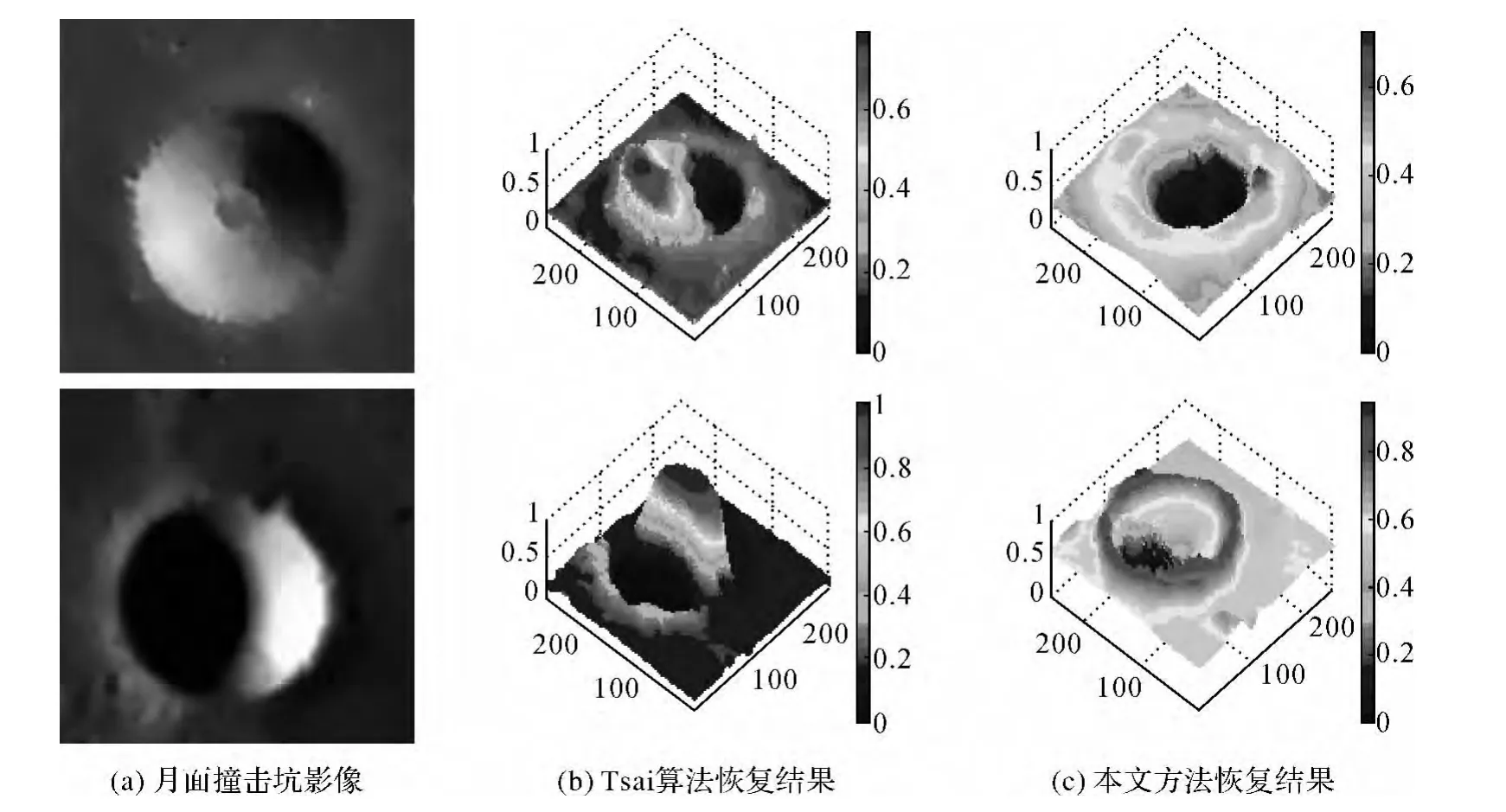
图6 月面影像三维恢复
由图6可以看出,这两种算法对于阴影区域的恢复效果都比较差。由于SFS恢复过程中,需要首先根据影像中的像素灰度分别建立反射方程,而阴影区域的像素灰度实际上不符合月面反射模型特征,在此基础上建立的反射方程也是错误的,从而导致最终的三维恢复结果存在较大误差;此外,在影像中存在某些点的反射率突变,直接造成恢复结果的突变。因此,为保证恢复结果的精度,运用SFS技术进行三维恢复时,要求物体表面的反射率近似一致。虽然Tsai算法在现有SFS算法中对于实际地形的恢复效果最接近实际地形,但从测绘角度而言,该方法对于实际地形的恢复效果仍不能满足生产需要,而本文算法由于存在边缘梯度约束与撞击坑内部表面连续性约束,因此得到的恢复结果与实际地形更加接近。但由于透视投影下本文采用的反射模型与实际反射情况的偏差、光照方向估计偏差,以及SFS约束条件的求取等因素导致本文算法仍存在一定的恢复误差。
五、结束语
本文研究了月面影像的特点,以及通过匹配进行月面地形恢复的局限性,分析了通过计算机视觉中SFS技术进行月面地形恢复的可行性。在对透视投影情况下SFS算法进行深入研究的基础上,建立了透视投影下的反射方程,以Lommel-Seeliger反射模型为基础,通过月面影像中存在的特征信息,实现了对反射方程的正则化约束,最终实现了对月面地形的三维恢复。采用Matlab模拟影像和真实月面影像对本文算法的正确性进行了测试。试验证明,本文算法在模拟影像情况下的恢复结果与真实值非常接近,验证了算法的正确性。此外,相对于其他SFS算法,本文算法对于实际月面影像有更好的恢复效果。SFS技术用于地形恢复不仅可以丰富测绘手段,也可为我国深空探测领域中测绘方面的问题提供一定的技术储备。
[1] 欧阳自远,李春来,邹永廖,等.中国月球探测二期工程科学目标的研究[C]∥中国宇航学会深空探测技术专业委员会第一届学术会议论文集.北京:[s.n.],2005:1-8.
[2] 叶培建,张火高,饶炜.积极应对深空探测的技术挑战[C]∥中国宇航学会深空探测技术专业委员会第二届学术会议论文集.北京:[s.n.],2005:1-8.
[3] 孙敏,胡争.基于向量匹配的稀疏深度图生成算法[J].测绘学报,2011,40(1):90-95.
[4] 李壮,雷志辉,于起峰.基于梯度径向夹角直方图的异源图像匹配[J].测绘学报,2011,40(3):318-325.
[5] PRADHAN R,GHOSE M K,JEYARAM A.Extraction of Depth Elevation Model(DEM)from High Resolution Satellite Imagery Using Shape from Shading Approach[J].International Journal of Computer Applications,2010,7(12):40-46.
[6] BURT P J,ADELSON E H.High-frequency Shape and Albedo from Shading Using Natural Image Statistics[C]∥IEEE Conference on Computer Vision and Pattern Recognition.Los Angeles:[s.n.],2011:2521-2528.
[7] KHUU S K,KHAMBIYE S.The Influence of Shape from Shading Information on the Perception of Global Motion[J].Vision Research,2012,55(15):1-10.
[8] 欧阳自远,胡浩,王世杰,等.月球科学概论[M].北京:中国宇航出版社,2005:38-40.
[9] TANKUS A,SOCHEN N,YESHURU Y.Shape from Shading under Perspective Projection[J].International Journal of Computer Vision,2005,63(1):21-43.
[10] TSAI P S,SHAH M.Shape from Shading Using Linear Approximation[J].Image and Vision Computing,1994,12(8):487-498.
[11] 杨杰,邓志鹏,郭英凯,等.两种新的光照方向估计方法[J].上海交通大学学报,2002,36(6):894-896.

