预期对房价的门限效应分析

古丽斯坦 路 畅 柳 杨

（1.中南财经政法大学 金融学院，湖北 武汉 430073；2.深圳房地产评估中心 博士后工作站，广东 深圳 518000）

一、引言

自1998年住房分配货币化改革后，我国主要城市的住房价格均出现了快速上涨。住房价格上涨过快不仅会影响我国经济的平稳发展，还可能影响我国的经济安全。近年来，稳定住房价格已成为宏观经济政策调控的主要目标之一。要使住房价格的调控政策更具针对性，需要对住房市场的特点及住房价格的波动机制进行深入研究。本文将重点分析不确定预期下住房价格的变动。

在有关预期对住房价格影响的文献中，有学者认为预期是房价波动的主要原因，也有学者认为房价波动的主要原因是经济基本面而不是预期。周京奎构建了中国的房地产投机理论模型，并结合我国14个城市的面板数据进行实证分析。研究结果表明，房地产市场投机行为是导致我国房价快速上涨的主要原因，而投机行为则主要受房地产价格预期的影响［1］。梁云芳、高铁梅结合我国35个大中城市1994～2006年的年度房地产市场相关数据，分别研究了东部、中部、西部地区房价波动的差异，并试图解释造成这一差异的原因，认为经济基本面因素对中部地区房地产市场价格有着显著的影响，预期因素则对东部地区房地产市场的短期价格波动有着显著的影响［2］。任荣荣、郑思齐和龙奋杰结合我国35个大中城市1999～2005年的房地产市场的相关数据，分析了房地产市场预期对房地产价格的作用机制，研究结果表明，房地产价格预期对房地产价格的变动有着显著的影响［3］。况伟大在住房存量调整模型的基础上，对我国35个大中城市1996～2007年数据分析发现，经济基本面对房价的影响要大于预期和投机行为［4］。刘江涛、张波和黄志刚发现投资预期在很大程度上抵消了限购政策的效果［5］。任超群、吴璟和邓永恒发现房价的大部分波动是由租金引起的，且市场繁荣时期预期对房价的推动作用要大于市场平稳时期［6］。崔红宇和戴金平对我国房地产干预政策效果进行了分析，认为房地产干预政策的出台短期内会影响购房者的预期［7］。

由上述文献可知，学者们对于预期对房价的影响尚存争议，在分析预期对房价的影响时不加以区分地进行线性处理，所得的结果可能是不准确的。而现有文献在处理非线性问题时，通常采用主观分组的方法，而该方法也可能导致分析结果的不准确。为避免人为划分区间所产生的偏误，本文拟采用Hansen提出的面板门限模型，根据数据自身的特点内生划分区间，并进一步分析预期对房价的门限效应［8］。

本文的后续部分安排如下：第二部分，简介理论模型的形式、面板门限模型的原理以及预期变量的测度。第三部分，在理论模型的基础上，结合35个大中城市历年的房地产市场相关数据，检验我国房地产市场的门限效应。第四部分为研究结论与政策建议。

二、理论模型与变量选择

1.模型设计。借鉴况伟大的研究成果［4］，房价决定模型可表达为：

式（1）中，Pt为第t期的住房价格；为住房市场参与者在第t期对第t+1期住房价格的预测，主要考察预期对房价的影响；ecot为经济基本状况（通常为居民人均收入或人均GDP），主要考察经济基本面对房价的影响；popt为当期期末总人口，主要考察人口规模对房价的影响；landt和poft分别为t期的土地成本和房屋建造成本，主要考察成本因素对房价的影响；Ai，t-1表示第t-1期住房存量，考查上期住房存量变动对本期房价变动影响；et为白噪音项。

通常对于房价决定模型的研究止步于模型（1）。事实上，我国各地区经济发展水平存在一定的差异，而预期的形成在一定程度上与当地的经济、政治及文化环境有关。因此，预期对房价的影响可能因经济发展状况的不同而呈现非线性特征。

为避免人为划分样本区间所产生的偏误，本文采用Hansen提出的面板门限模型的方法，通过内生划分样本区间，进而考察不同经济发展水平下预期对房价影响。接下来，以单门限模型为例，简要介绍关于房价的面板门限模型。根据面板门限模型的基本理念，房价的单门限模型可表示为：

式（2）中，I（＊）为一指标函数，当条件满足时取1，否则取0。λ为门限值；X 为一系列影响房价的因素（如人口规模、建造成本等）。门限模型的基本思路如下：

首先，不断地根据门限值λ将样本分为两组，并运用最小二乘法得到各参数的估计值及其残差平方和S（λ）。使S（λ）最小的门限值λ，即为模型的门限估计值，其残差的方差为。

其次，在得到门限参数的估计值后，还需要对门限值的显著性和真实性进行检验。对门限值显著性的检验方法如下：

原假设H0：φ1=φ2，备择假设为H1：φ1≠φ2。其检验统计量为：。其中，S0为H0下的残差平方和。然而，在原假设H0下，统计量F 的分布是非标准的，Hansen建议采用“自抽样法”（bootstrap）来获得其渐进分布，进而得到相应的P值。若原假设H0被拒绝，则表明模型存在明显的门限效应。

对门限值真实性的检验方法如下：

以上为单门限模型门限值检验的基本思路。在实际研究过程中，经常会出现多门限的情况。多门限模型的门限值估计与单门限模型的有所不同，下面以双门限模型为例：

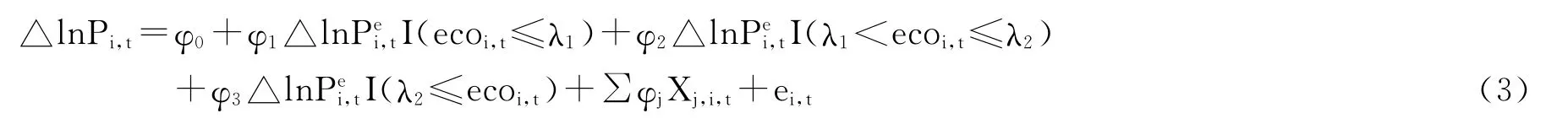
就双门限模型而言，对于任意给定的（λ1，λ2），根据最小二乘法估计其残差平方和S（λ1，λ2），并得到使S（λ1，λ2）最小的（λ1，λ2）。需要特别指出的是，第二个门限值的估计值具有一致性，但第一个门限估计值不具备该性质。因此，在得到后，需要根据进行再次估计，由此得到第一个门限的渐进有效估计量。双门限模型的假设检验与单门限模型相似。此外，双门限模型也可以很容易地扩展至多门限模型，限于篇幅，不再赘述。

2.房价预期的测度。近年来，关于房价预期的测度方法主要有：适应性预期、不确定预期（半理性预期）和理性预期。而理性预期假设条件过于严格，在实际研究过程中难以实现。因此，本文采用适应性预期和不确定预期两种预期测度方法来测算房价预期。关于适应性预期的测度，不少学者主张适应性预期作为住房市场的价格预期［3］［9］。使用适应性预期方法构建住房价格预期，可表示为：

关于不确定预期的测度，李拉亚认为预期由两部分构成：预期模型的结构和包含预期的不确定性的表达式［10］。徐文政、盛宇华也确定了经济预期中不确定性的重要性［11］。所以，本文认为通过传统预期理论得出的预期形式只是预期的一部分。此外，不确定性也是预期的重要组成部分。本文尝试将不确定预期引入住房市场。根据李拉亚关于预期的研究，预期的形成来源于如下两个方面：（1）过去的经验总结；（2）对现有及未来信息的不确定［12］。据此，住房市场的价格预期可表示为：

3.门限变量的选择。本文选择经济发展状况作为门限变量，主要原因是：预期对房价的影响可能因为经济发展状况的不同而呈现非线性的特征。一般而言，在经济发展相对平稳时期预期与房价呈正相关；而在经济波动较大的时期，预期与房价之间不存在显著而稳定的相互关系。此外，任超群等发现经济平稳时期预期对房价的影响要小经济繁荣时期。另一方面，房价对预期的影响也可能随着经济发展状况的不同而有所差别［6］。

4.本文所使用的模型。根据前文的分析，本文将分别采用居民收入和GDP作为门限变量分析适应性预期和不确定预期对房价影响，由此构造如下4个模型（由于门限的数量尚未确定，这里以双门限模型为例）。

三、实证分析

1.数据来源。本文使用中国35个大中城市2001～2012年间平均住房价格、人均工资收入、利率、住房销售面积、住房新开工面积、住房竣工价值、土地开发投资额等统计数据。此外，还根据前文介绍的外推预期模型、适应性预期模型和不确定预期模型计算得出了收入和房价的预期数据。为消除通货膨胀影响，本文将相关名义变量（房价、住房建造价值和住房开发完成投资）经CPI调整后转化为实际变量。各变量的含义、用途及来源如表1所示，各数据的结构如表2所示。

表1 各变量的含义、用途及来源

表2 各变量的数据结构

2.单位根检验。为避免出现虚假回归，在对模型进行回归分析之前，需要对住房需求计量模型所涉及的数据进行单位根检验。由于本文使用的数据均为面板数据，因此需要对数据进行面板单位根检验。通常面板单位根的检验方法有以下四种：Levin-Lin-Chu（LLC）检验、Im-Pesaran-Shin（IPS）检验、Fisher-Dfuller（ADF）检验和Fisher-Phillips-Perron（PP）检验。其中，LLC 检验为同质面板单位根检验，LPS检验、Fisher-ADF和Fisher-PP检验则为异质面板单位根检验。为避免在后续回归分析中出现异方差问题，在单位根检验前，将所有变量转换为自然对数形式。检验结果显示，各变量在一阶差分序列均平稳，符合建模要求。各个变量的面板单位根检验的结果如表3所示。

3.门限值的确定及检验。对于面板门限模型而言，首先要确定的是门限的个数，以便确定模型的形式。本文分别在“不存在门限”，“存在一个门限”和“存在两个门限”的设定下对式（7）-（10）进行估计，所得的F统计量和使用“自抽样法”得出的P值，由表4所示。

表3 面板单位根检验结果

表4 各模型的门限检验结果

由表4可知，上述4个模型中模型1和模型4为双门限模型，模型2为三门限模型，模型3为单门限模型。在模型1中，在单门限、双门限和三门限的假设下，通过Bootstrap方法（500次）得到的F统计量分别为55.60、10.894和5.012，与之相对应的P值分别为0.00、0.00和0.31，即显著拒绝了“没有门限值”和“存在一个门限值”，但没有拒绝“存在两个门限值”的假设，因此，可以认为模型1存在2个门限值，为双门限模型。模型2、模型3和模型4门限值数量的判断与模型1的原理类似，这里不再赘述。从结果来看，上述4个模型中模型1和模型4为双门槛模型，模型2为三门限模型，模型3为单门限模型。

借助似然比函数图，可以更为清晰地反应门限值的估计和置信区间的构造过程。门限参数的估计值是指似然比检验统计量LR 最小时门限值的取值，如图1所示。在图1中，虚线表示似然比统计量（LR）的临界值。根据Hansen的建议，只有当门限值的估计值位于LR 统计量以下时，其估计值才是有效的。而上述4个模型的LR 统计量的最小值均在临界值之下（LR 的最小值小于临界值）。因此，可以认为4个模型的门限值的估计值是有效的。4个模型的门限值的估计结果由表5所示。

如表5可知，模型1有2个门限值分别为0.10和0.14；模型2有3个门限值，分别为0.11、0.14和0.17；模型3有1个门限值为0.08；模型4有2个门限值，分别为0.10和0.12。

图1 各模型的门限参数的估计及其置信区间

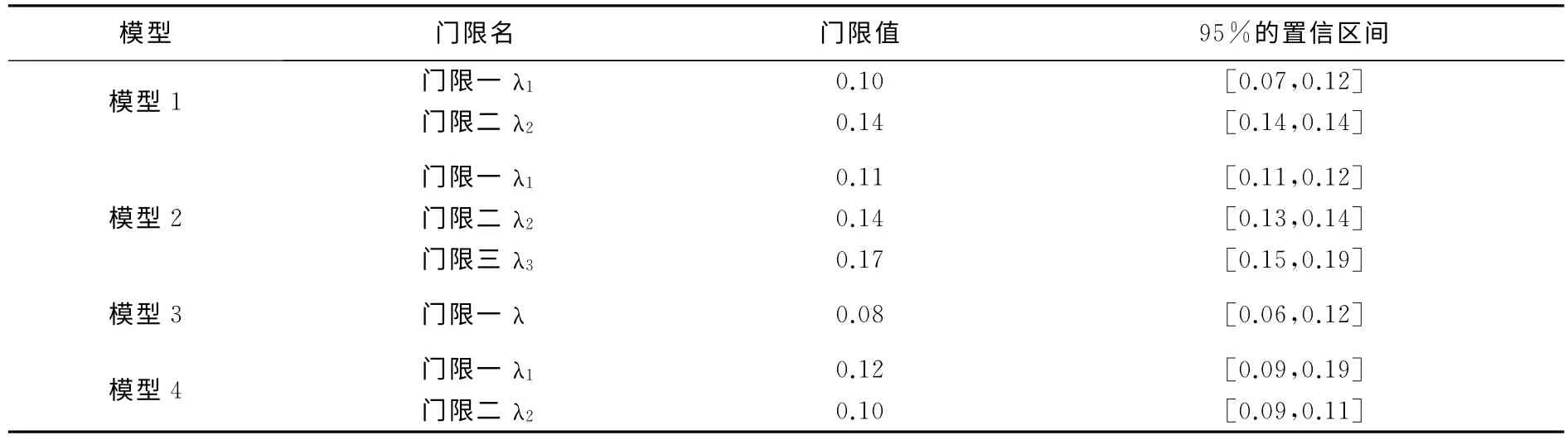
表5 各模型的门限值估计结果

4.模型估计结果。根据上述门限值估计结果可将模型1的门限变量（适应性预期）分为3组；模型2的门限变量（适应性预期）分为4组；模型3的门限变量（不确定预期）分为2组；模型的4的门限变量（不确定预期）分为3组。其具体估计结果如表6所示。

由表6可知，总体来看，适应性预期模型（模型1和模型2）中，预期对房价的影响随收入或GDP增长率的上升而下降；不确定预期模型（模型3和模型4）中，预期对房价的影响随收入或GDP 增长率的上升而上升。

模型1检验了不同收入增长速度的条件下，适应性预期对房价的影响。结果显示，在收入增长的不同阶段预期对房价存在明显的门限效应。具体而言，在收入增长幅度较低时，预期增长率变动对房价增长率变动的影响较大，在收入增长幅度较高时，预期增长率变动对房价增长率变动的影响较小（β1=1.02，t=48.33；β2=0.94，t=46.87；β3=0.73，t=40.41）。这说明在适应性预期的条件下，收入对房价的影响随着收入增长率的增加而减少。

表6 各模型的面板门限效应估计结果

模型2检验了不同GDP增长速度的条件下，适应性预期对房价的影响。结果显示，在收入增长的不同阶段预期对房价存在明显的门限效应。具体而言，在GDP增长幅度偏低时，预期增长率对房价变动率的影响较大，在GDP增长幅度偏高时，预期增长率对房价变动率的影响较小（β2=0.95，t=40.39；β3=0.78，t=43.91）。但在GDP增长幅度最缓和最剧烈的阶段，预期增长率变动对房价增长率的变动的影响不显著（β1=0.96，t=0.44；β4=0.78，t=0.84）。这说明在适应性预期的条件下，在GDP增长的最缓和与最剧烈时，预期对房价无明显影响。在GDP增长的温和阶段，预期对房价的影响随GDP增长率的增加而减少。

模型3检验了不同收入增长速度的条件下，不确定预期对房价的影响。结果显示，在收入增长的不同阶段预期对房价存在明显的门限效应。具体而言，在收入增长率变动较低时，预期增长率变动对房价增长率变动的影响较小，在收入增长率变动较高时，预期增长率变动对房价增长率变动的影响较大（β1=0.15，t=2.47；β2=0.48，t=6.79）。这说明在不确定预期的条件下，预期对房价的影响随预期增长率的增长而增加。

模型4检验了不同GDP增长速度的条件下，不确定预期对房价的影响。结果显示，在收入增长的不同阶段预期对房价存在明显的门限效应。具体而言，在GDP增长率变动较低时，预期增长率对房价变动率的影响较小，在GDP 增长率变动较高时，预期增长率对房价变动率的影响较大（β1=0.38，t=1.99；β2=0.54，t=4.86）。但在GDP 增长率的剧烈变动阶段预期增长率对房价增长率的变动影响不显著（β3=0.50，t=0.35）。这说明在不确定预期的条件下，预期对房价的影响随预期增长率的增长而增加。但在预期增长率达到一个较高水平时，预期对房价的影响将不再显著。

就其他控制变量而言，投资增长率变动与房价增长率的变动正相关；收入增长率的变动与房价增长率的变动正相关：利率的变动与房价增长率的变动正相关。这与之前的多数研究结论一致。而人口规模增长率的变动和住房销售面积增长率的变动与住房价格增长率的变动之间，并无显著的相关关系。

四、结论与建议

本文在Hansen面板门限模型的基础上，结合我国35个大中城市的相关面板数据，检验了适应性预期和不确定预期条件下，不同收入和GDP增长阶段，预期对房价的门限效应，得到结论如下：（1）预期对房价存在明显的门限效应。研究表明，在不同收入或GDP增长率的条件下，预期对房价影响表现为显著的非线性特征。（2）不同预期条件下，预期对房价的门限效应有所不同。适应性预期模型（模型1和模型2）中，预期对房价的影响随收入或GDP增长率的上升而下降；不确定预期模型（模型3和模型4）中，预期对房价的影响随收入或GDP增长率的上升而上升。

虽然影响房价的因素有很多，但是住房市场不同于其他市场，居住问题关系到国计民生，关系到广大民众的基本生活需求，对于制定调控政策的政府而言，必须认识到市场预期对于房价的重要影响。为了促进我国房地产业的健康发展，本研究对于制定房地产市场相关调控政策具有以下启示：（1）在房地产市场发展的不同阶段，政府需要根据不同的市场预期条件制定相应的调控政策。（2）政府需要建立一套完整的调节机制，对公众的市场预期加以适当引导，以促进房地产市场能够健康、平稳发展。

［1］周京奎.房地产价格波动与投机行为——对中国14城市的实证研究［J］.当代经济科学，2005，（4）：19—24.

［2］梁云芳，高铁梅.中国房地产价格波动区域差异的实证分析［J］.经济研究，2007，（8）：133—141.

［3］任荣荣，郑思齐，龙奋杰.预期对房价的作用机制：对35个大中城市的实证研究［J］.经济问题探讨，2008，（1）：145—148.

［4］况伟大.预期、投机与中国城市房价波动［J］.经济研究，2010，（9）：67—78.

［5］刘江涛，张波，黄志刚.限购政策与房价的动态变化［J］.经济学动态，2012，（3）：47—54.

［6］任超群，吴璟，邓永恒.预期对租金房价比变化的影响作用研究——基于住房使用成本模型的分析［J］.浙江大学学报（人文社会科学版），2013，（1）：58—72.

［7］崔红宇，戴金平.我国房地产干预政策效果分析［J］.河北经贸大学学报，2013，（5）：95—98.

［8］Hansen B E.Threshold Effects in Non-dynamic Panels：Estimation，Testing and Inference［J］.Journal of Econometrics，1999，93（2）：345—368.

［9］况伟大.房地产投资、房地产信贷与中国经济增长［J］.经济理论与经济管理，2011，（1）：59—68.

［10］李拉亚.预期与不确定性的关系分析［J］.经济研究，1994，（9）：12—19.

［11］徐文政，盛宇华.预期组合：将不确定性纳入与其理论的新方法［J］.南京社会科学，2011，（8）：44—48.

［12］李拉亚.理性疏忽、粘性信息和粘性预期理论评介［J］.经济学动态，2011，（2）：117—124.