壁面小折角对马赫数4.5边界层中扰动演化的影响

吴宁宁，罗纪生

（天津大学 力学系，天津 300072）

0 引 言

高超声速边界层转捩位置的预测是飞行器设计中的关键问题之一，该问题的研究具有重要理论意义。目前比较常用的转捩预测方法是以流动稳定性理论为基础的eN方法，该方法一般用于边界层流向变化缓慢的流动。

由于设计需要，飞行器表面存在小折角，包括小扩张角和压缩角。由于边界层中的流动在折角处变化较快，导致在边界层中传播的小扰动经过折角时，其幅值、波长都会受到影响。因此，在折角附近不满足流动稳定性理论，稳定性计算得到的N值存在误差。工程上采用的eN方法是忽略流场在折角处的突变，直接积分增长率得到N值。这样简单的处理会引起误差，进而对转捩位置产生影响。因此，研究壁面小折角对高超声速边界层中扰动演化的影响，并对eN方法进行修正，具有重要的工程应用价值［1－6］。

本文采用数值模拟和流动稳定性的方法，研究了来流马赫数 Ma＝4.5，折角分别为±1°，±2°，±3°（正为压缩角、负为扩张角）的扰动演化情况，考察了不同折角角度对不同频率的扰动波的影响，根据流动稳定性理论预测了折角前后不稳定扰动波的演化，并对某些影响eN方法的情况进行分析，给出了N值的修正系数。

1 控制方程和数值方法

1.1 计算模型及控制方程

计算模型如图1所示，定义压缩角为正，扩张角为负。

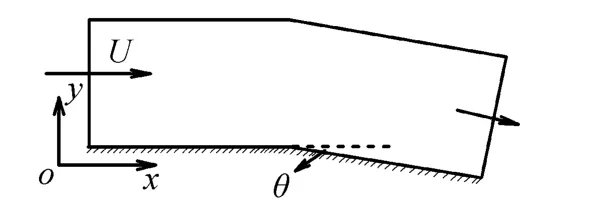
图1 扩张角和压缩角模型Fig.1 Expansion angle and compression angle model

控制方程为可压缩守恒型Navier－Stokes方程组，将直角坐标系（x，y）变换到贴体坐标系（ξ，η）下，贴体坐标系下的控制方程的形式为：

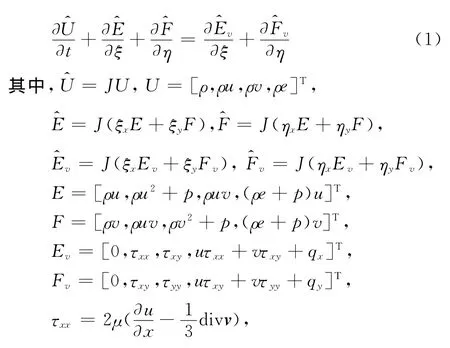
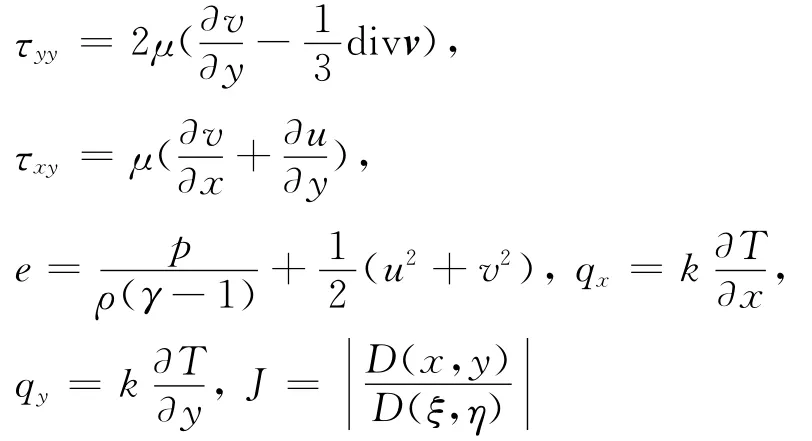
为了叙述方便，采用（x，y）表示贴体坐标系下流向和壁面法向坐标。

1.2 数值格式

计算基本流时采用守恒型N－S方程中，对流项采用通量分裂，五阶WENO格式进行计算，粘性项采用六阶中心差分格式，时间项采用三阶TVD的Runge－Kutta格式。壁面采用无滑移绝热条件，出口采用外推边界条件。计算扰动演化时采用扰动方程进行计算，即将N－S方程中的守恒变量看作基本流加扰动的形式带入方程，去掉基本流的项，通过化简得到扰动方程，直接求解扰动量。在求解时，对流项差分格式采用McCormack格式，粘性项采用六阶中心差分格式，时间项采用6阶Runge－Kutta格式。计算域出口采用嵌边函数边界条件［7－8］。

基本流的计算：采用直接数值模拟进行计算，先计算折角上下游比较长范围内的流场，流向、法向均采用非均匀网格，在折角附近及壁面附近网格较密。然后，从所得稀流场中选取折角附近的流场，再进行加密计算，得到用于研究小扰动演化的基本流场。这样做是为了排除入口马赫波的影响。定义折角处为坐标原点，计算域入口为x＝－50。

1.3 线性稳定性理论

得到基本流后，在计算域入口引入给定频率的不稳定扰动波，不稳定扰动波是以计算域入口的流场为基本流，采用线性稳定性理论计算得到的。设小扰动可以写成行进波的形式，本文研究二维扰动，所以，入口处的小扰动波可以写成如下形式：

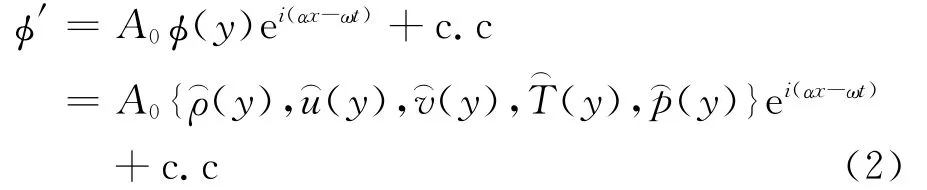
其中，φ′＝ ｛ρ′，u′，v′，T′，p′｝表示扰动量，A0为小扰动幅值，ω 为频率，α为线性扰动方程的特征值，为相应的特征函数。计算采用空间模式，α为复数，实部αr表示流向波数，负的虚部 －αi为扰动幅值的增长率，记为σ。

对某一流向站位采用线性稳定性理论（LST）计算其特征值和特征函数，调整扰动波频率，得到增长率为零的频率即为此站位的中性曲线点。计算不同的站位的中性曲线点，即可得到整个流场的中性曲线［9－10］。

1.4 修正系数ΔN

根据扰动方程数值模拟（DNS）的结果可以得到扰动幅值A沿流向的演化，由此得到扰动幅值沿流向的增长率。在折角上游，由于流动是渐变的，线性稳定性理论（LST）预测的扰动幅值的增长率与数值模拟（DNS）是一致的；在折角的附近，由于折角突变的影响，LST得到的结果与DNS不一致；当流动到达折角下游，流场恢复渐变的性质，因此在折角下游某一站位后，LST的计算结果将会与DNS一致，即从此位置开始，扰动幅值的增长率可以采用LST方法计算。

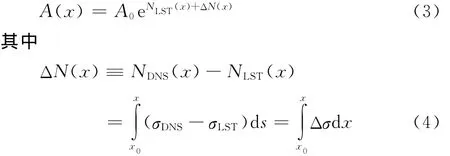
σDNS、σLST分别为采用DNS和LST计算得到的扰动幅值增长率，在折角附近处Δσ不为零，其它位置处为零。因此，当x达到过折角后某一站位，ΔN将趋于常数，称其为折角对N值的修正。对于给定的来流条件，N值修正与折角和扰动频率有关。

1.5 计算工况

为了工程的需要，应该对N值修正进行系统计算。作为初步研究，本文针对来流马赫数Ma＝4.5，温度T∞＝255.7K，以入口边界层位移厚度δ为特征长度无量纲化，其雷诺数Re＝1×105，折角θ＝±1°，±2°，±3°，初始扰动幅值A0＝1×10－6，研究了第一模态、第二模态不稳定扰动波过折角的线性演化，并分析折角θ对修正系数ΔN（x）的影响，给出了不同折角和频率下的N值修正。

2 计算结果及分析

2.1 程序验证及网格无关性检验

首先，对数值模拟计算程序进行验证，采用平板边界层扰动演化进行验证。图2（a）为频率ω＝2.2，DNS和LTS计算所得到的平板边界层中扰动幅值演化结果。由图可知，DNS与LST的计算结果吻合的很好，验证了数值模拟程序的正确性。其次，进行网格无关性检验，分别采用法向网格数为251、401，流向网格相等的两套网格进行扩张角1°，频率ω＝1.92的扰动波演化计算。

图2（b）为两套网格所计算的扰动波幅值演化结果。结果表明，法向网格取251时，可以满足计算精度要求。下述计算结果都采用此网格。

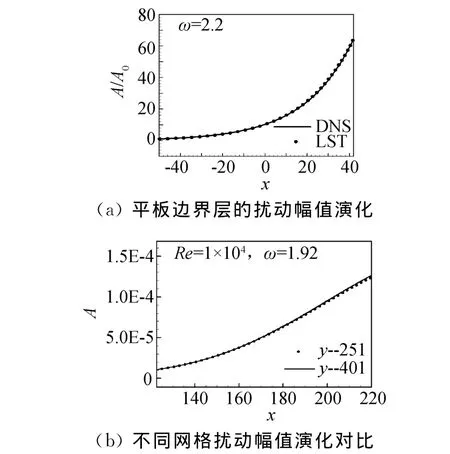
图2 平板边界层及不同网格的扰动幅值演化Fig.2 Disturbance amplitude evolutions

2.2 扩张角对第二模态扰动波的影响

来流马赫数为4.5时，根据模态分析理论，第二模态扰动波的增长率较大，是引起转捩的主要因素。首先考虑第二模态扰动波的情况。

为了便于分析，在计算扰动波的演化之前，采用流动稳定性理论（LST）计算带扩张角流动的中性曲线，其中所用基本流采用直接数值模拟（DNS）计算，由中性曲线可得扰动经过扩张角后的演化情况，为进一步数值模拟提供依据。图3（a）给出了扩张角为1度的边界层中第二模态不稳定扰动的中性曲线（DNS）和平板边界层（BLXS）中性曲线对比。其中，虚线为采用平板布拉修斯解作为基本流，采用流动稳定性理论所求得的中性曲线；实线为采用直接数值模拟求得的扩张角流动作为基本流，采用流动稳定性理论所求得的中性曲线。由图可知，在x＝0处，即扩张角站位，由于基本流局部变化较快，流动稳定性理论不再适用。在扩张角上下游，如x＜－20、x＞50的范围内，中性曲线变化比较平缓，可以采用流动稳定性理论计算扰动演化。

由图3可知，当存在扩张角时，中线曲线在过扩张角后，其上下两支同时向频率减小的方向偏折，表明扩张角使原来高频的不稳定扰动波变成稳定状态，而原来处于稳定状态的低频扰动波变成不稳定状态，即扩张角前的不稳定扰动波经过扩张角后很快就变为衰减波。经计算发现，频率ω＝1.92是增长区间最长的不稳定波。图3（b）、（c）、（d）分别为频率ω＝1.92的扰动波幅值、增长率和修正系数ΔN沿流向的演化，实线和虚线分别代表直接数值模拟（DNS）和流动稳定性理论（LST）的计算结果。

由图3（c）可得，在扩张角之前，DNS和LST计算的扰动增长率吻合的很好，即扰动波的演化规律符合线性稳定性理论；在扩张角处，由于基本流流向变化急剧，不满足流动稳定性理论，DNS和LST计算的增长率差别很大；在扩张角后的某流向站位，流动变化渐趋平缓，DNS和LST计算的增长率相符合。根据1.4节公式（4）可以计算出修正系数ΔN 为－0.2左右，如图3（d）所示。由于频率ω＝1.92是增长区间最长的不稳定波，其它频率不稳定扰动波的增长区间都比较短，扰动波很快就衰减，因此不需要对N值进行修正。

图4为扩张角2°、3°的计算结果。图4（a）和（b）分别为2°、3°的中性曲线对比，实线和虚线的计算方法和所代表的意义同扩张角1°类似。由图中可知，中性曲线上下两支的下移程度随扩张角的增大而增大，即扩张角之前的增长波过扩张角后变为衰减波。图4（c）和图4（d）为频率ω＝2.0的扰动波的幅值演化，其增长衰减趋势满足中性曲线。由于扩张角前增长的扰动波过扩张角后全部衰减，因此采用eN方法预测转捩时，不用对N值进行修正。

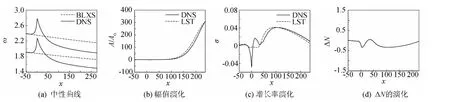
图3 扩张角为1°的第二模态扰动的中性曲线和ω＝1.92扰动的演化Fig.3 Neutral curves in second mode and the curves of disturbance evolution（θ＝－1°，ω＝1.92）

综上所述，通过对不同扩张角的计算分析可得，对上游不稳定扰动波，扩张角相当于一个阻断器，阻断了不稳定波的增长；对下游稳定扰动波，扩张角相当于扰动发生器，使得原来一些低频的稳定扰动波变成不稳定状态。因此，采用eN方法计算带有小扩张角流动的N值时，扩张角之前可以按eN方法计算N值；在扩张角之后，会出现新的低频不稳定波，计算N值时要考虑这些新的低频不稳定波。总之，遇到小扩张角时，可以采用常规eN方法计算N值预测转捩位置，但是需要考虑新出现的低频不稳定波。

2.3 压缩角对第二模态扰动波的影响

图5给出了压缩角为1°的第二模态扰动波的中性曲线及其沿流向的幅值演化。其中，图5（a）为中性曲线，两条中性曲线的计算方法如2.2节扩张角所述。由图5（a）可得，与扩张角所得结论相反，压缩角使得中性曲线上下两支向上偏折，即压缩角后的不稳定扰动波频率增大，产生了高频不稳定波。

选择过压缩角后有足够增长区间的不稳定扰动波进行计算，在此选择频率为2.1、2.2、2.3的扰动波，分别采用数值模拟（DNS）和流动稳定性（LST）方法计算幅值演化。图5（b～d）为相应频率扰动波的幅值演化，图5（e～g）为相应的扰动幅值增长率演化。由图可知，在压缩角后某一站位，即x＞100处，线性稳定性理论（LST）和直接数值模拟（DNS）计算出的增长率完全吻合，仅仅在压缩角附近产生差别。这表明从此站位开始可以采用流动稳定性理论（LST）预测扰动演化，即可以采用eN方法计算N 值预测转捩，但在压缩角附近需要对N值进行修正。采用1.4节公式（4）可以计算得到不同频率的修正系数ΔN，如图5（h）所示。可知，当x＞100时，修正系数ΔN为常数，即为该频率下的修正系数值。在此工况下，修正系数ΔN 的范围为－0.6～0.6。由于无法对所有频率进行计算，在此所得的范围仅为本文所计算频率下的数值，只是一个定性的结果，定量的结果有待于进一步计算。

采用同样的方法，计算压缩角为2°、3°对第二模态扰动波的影响。图6给出了压缩角为2°、3°的中性曲线和幅值演化。图6（a）和（b）分别是压缩角为2°、3°的中性曲线。其中，实线和虚线的计算方法同2.2节扩张角。由图可得，过压缩角后中性曲线向上偏移程度随压缩角的增大而增大。压缩角前不稳定扰动波过压缩角后全部衰减，中性曲线闭合。进一步计算发现，在下游距离压缩角较远的位置处不稳定扰动区域再次出现，形成中性曲线在压缩角下游断开的现象。这是因为随着压缩角的增大，其对下游的速度剖面产生影响，进而影响扰动的增长特性。在距离压缩角较远的下游，流动受压缩角影响较小，不稳定区域再次形成。选取频率为2.0的不稳定扰动波，分别采用直接数值模拟（DNS）和流动稳定性理论（LST）进行计算。图6（c）和（d）为幅值演化结果，实线和虚线分别代表DNS和LST的计算结果。扰动波的增长和衰减趋势与中性曲线的预测相吻合。

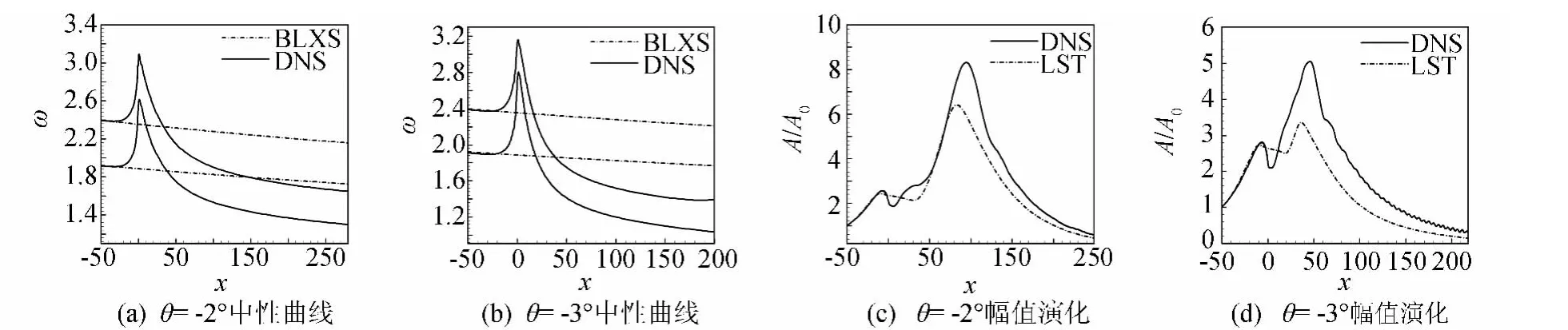
图4 扩张角为2°、3°第二模态扰动的中性曲线及幅值演化曲线（ω＝2.0）Fig.4 Neutral curves in second mode and the curves of amplitude evolution（ω＝2.0）

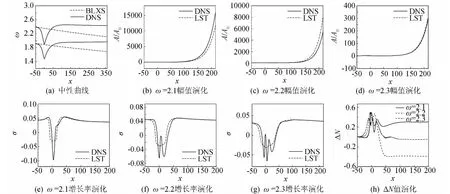
图5 压缩角为1°第二模态扰动的计算结果（θ＝1°）Fig.5 Computational results of second mode（θ＝1°）

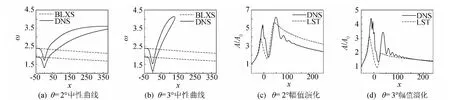
图6 压缩角为2°、3°的中性曲线和扰动幅值演化曲线（ω＝2.0）Fig.6 Neutral curves in second mode and the curves of amplitude evolution（ω＝2.0，θ＝2°、3°）

由上述分析可知，当压缩角为2°、3°时，不稳定扰动波过压缩角后全部衰减。因此，碰到压缩角大于1度的流场时，采用eN方法计算N 值时，不需要考虑对N值进行修正，可以采用常规方法计算，即忽略压缩角的影响，分别计算压缩角上下游的N值即可。

2.4 扩张角对第一模态扰动波的影响

如前所述，当马赫数为4.5时，依据模态分析理论，第二模态在转捩中占主导地位。采用eN方法计算N值时，主要考虑第二模态扰动波的增长率。为了研究扰动过扩张角和压缩角演化的机理，下面计算分析扩张角对第一模态扰动波的影响。

图7给出了扩张角为1°、2°、3°第一模态扰动波的中性曲线及频率ω＝0.65扰动波的幅值演化曲线。图7（a～c）中实线和虚线的计算方法如前2.2节所述。实线代表带扩张角的平板第一模态的中性曲线，虚线代表平板第一模态的中性曲线。可看出，扩张角对第一模态中性曲线的下支影响很小，这与靠近壁面部分的流向速度剖面过扩张角变化不大有关。扩张角使得中性曲线的上支向下偏折，即过扩张角后不稳定扰动波的频率范围变窄，其偏折程度随扩张角的增大而增大。当扩张角为3°时，在下游站位x＝180处中性曲线闭合，不稳定扰动波全部衰减。进一步计算发现，当x＝460时不稳定扰动区域重新出现，即出现了中性曲线断开的现象。这种现象与压缩角为3°第二模态的中性曲线类似。选取频率为0.65的扰动波，分别采用直接数值模拟（DNS）和流动稳定性（LST）计算幅值演化。图7（d～f）分别为频率ω＝0.65扰动波过扩张角为1°、2°、3°的幅值演化结果。过扩张角后扰动幅值虽然出现调制，但LST与DNS所计算的幅值演化趋势基本吻合，这表明，在扩张角后可以采用流动稳定性理论（LST）预测扰动的幅值演化。

由图7（d～f）可以看到，扩张角后扰动的幅值演化不再是单调的，而是在空间上被调制了。为了深入分析这一现象，我们特别研究了图7（f）的工况。根据波的传播理论，当小扰动波在空间传播时，如果传播介质随空间变化，扰动波的波数α将发生变化；如果传播介质随时间变化，将引起频率ω的变化。由于扩张角将会引起流场空间变化，因此频率ω不变，波数α发生变化。从计算结果分析，扩张角下游的扰动中有两个波数的扰动波。

为了证实ω不发生变化的结论，我们考察了扩张角后边界层中空间某一点（x＝55.3，y＝0.763）的扰动速度随时间的演化。图8（a）给出了扰动速度随时间的演化，图8（b）为时间域傅立叶变换的结果。可知，扰动波的周期T＝9.67、频率ω＝2π／9.67＝0.65，与计算域入口所加的扰动波频率一致。

下面给出扩张角对扰动波长影响的分析。由图7（f）可得，当边界层中存在扩张角时，幅值产生调制现象。在离扩张角较远的下游，调制是由两个波数的扰动引起的，这两个波数及扰动可以由直接数值模拟（DNS）所计算的特征值和特征函数得到，即我们将扩张角后的扰动形式写为

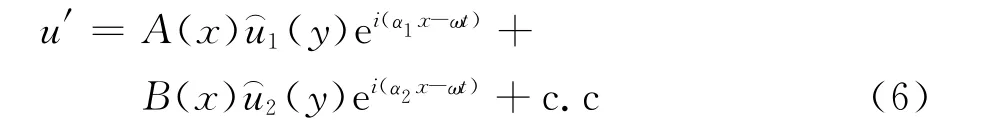
其中α1、α2为扰动方程的不同特征值，为对应的归一化后的特征函数，A、B分别为扰动的幅值。根据对图7（f）的分析可得｜B｜／｜A｜≈0.045，｜Δα｜＝｜αr1－αr2｜≈2π／34≈0.18，如图8（c）所示。

为了验证上述分析，我们对扰动速度进行空间域的傅里叶变换，变换的范围为x1＝41.2859到x2＝186.474，变换的基本波数α0＝2π／（x2－x1）＝0.04328。变换的结果如图8（d）所示，波数空间中出现两个峰值，分别对应n＝13，17，波数为0.5626和0.7357，波数差为0.1731，两波数幅值比为0.05，与分析的结果基本一致。

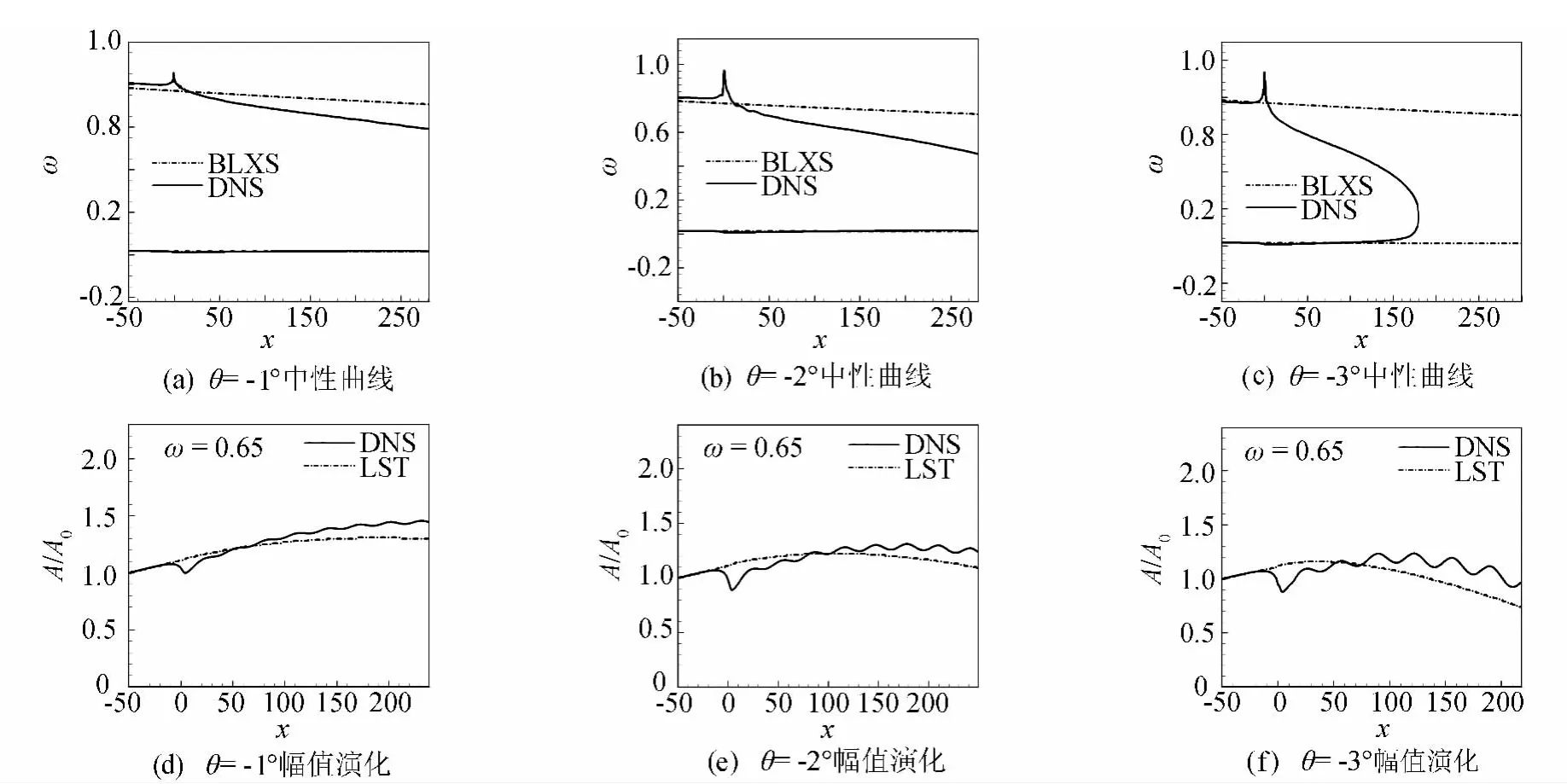
图7 扩张角为－1°、－2°、－3°的第一模态扰动波的中性曲线和扰动幅值演化曲线Fig.7 Neutral curves in first mode and the curves of amplitude evolution（θ＝－1°，－2°，－3°）

图8 时间域傅里叶变换和空间域傅里叶变换Fig.8 Time domain of Fourier transform and Fourier transform on spatial domain

为了验证这两个波数可以由线性稳定性理论（LST）的特征值得到，我们取x＝49.03处的流动作为基本流，用线性稳定性理论（LST）计算了该处的特征值和特征函数，对应频率ω＝0.65得到的两个特征值分别为：α1＝0.7384＋0.000242i，α2＝0.5414＋0.000056i，与数值模拟得到的波数基本一致，这两个特征值都是衰减的，但衰减率很小，特征函数分布如图9（a，b）所示。

图9（c）为将两个波数的波叠加，并与直接数值模拟进行对比的结果。带三角符号的虚线是两个波数的波叠加的结果（YZ），带正方形符号的虚线数值模拟（DNS）计算的结果。由图可知，两者吻合的很好，再一次证明上述分析是正确的。

总之，扰动通过扩张角后，可能产生不同波数的扰动，数值模拟得到的波数与用流动稳定性理论给出的结果基本一致，表明可以用流动稳定性理论的方法预测这些不同波数。流动稳定性理论给出的两个扰动波的衰减率都很小，因此在扩张角下游的一定区域内这些扰动波能同时存在，它们相互作用就会出现扰动幅值被调制的现象。如果扩张角下游只有一个扰动波是增长的或者衰减很慢，其它的扰动波衰减都较快，则在演化中这个扰动波的幅值将远大于其它扰动波的幅值，因而调制现象将会变得相对很弱，表现为扩张角后开始有调制的现象，但在远离下游处调制现象就会变得不明显，如图6（c，d）所示。

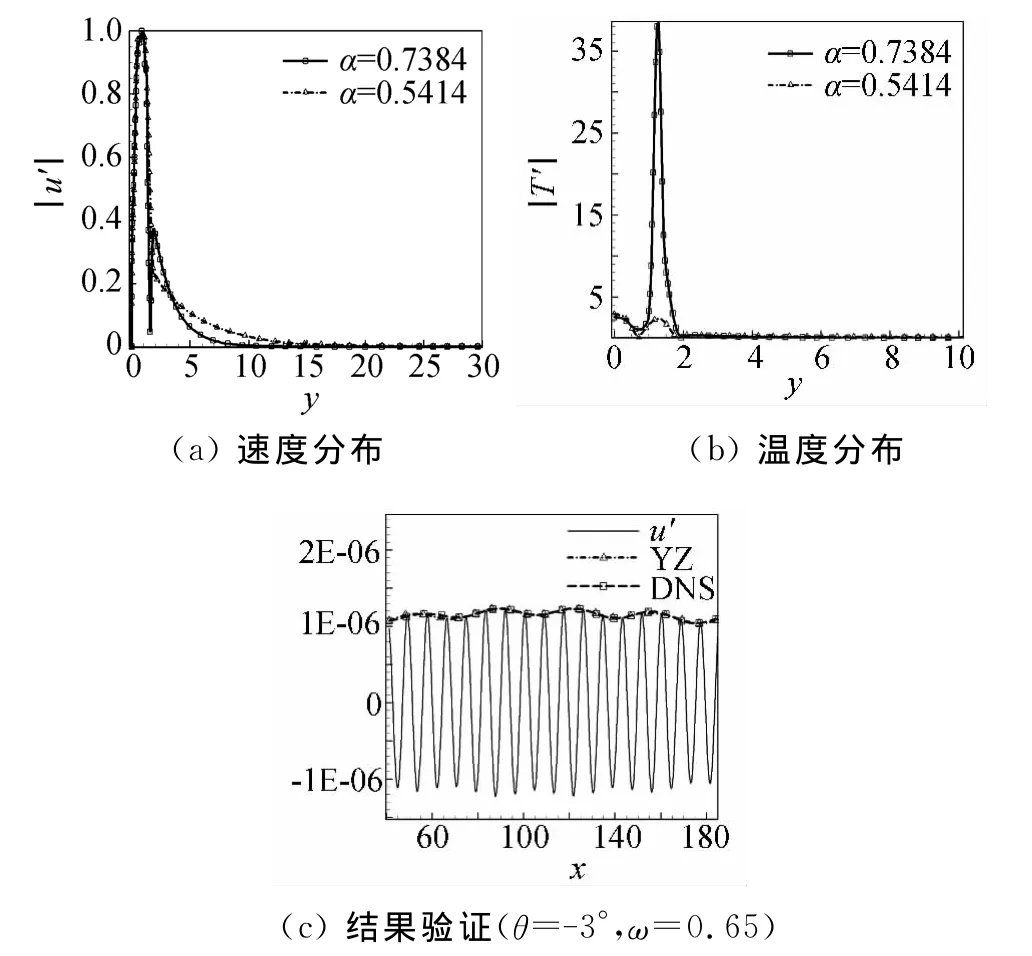
图9 特征函数和结果验证Fig.9 Eigen－function and Verification of results

图7（d～f）的结果表明，对于给定的频率，扩张角对扰动幅值的调制随角度增大而增大，但调制引起的幅值改变总量较小，不影响扰动总的增长或衰减的趋势。

综上，扩张角使得第一模态的不稳定波范围减小，扰动过扩张角后产生衰减。同时，在此工况下，第一模态扰动波的增长率很小，对转捩不起主导作用。所以，当采用eN方法计算带有小扩张角流场的第一模态N值时，不需要对N值进行修正。

2.5 压缩角对第一模态扰动波的影响

图10为压缩角1°、2°、3°第一模态扰动波的中性曲线、幅值演化和修正系数曲线。其中，图10（a～c）为中性曲线对比，图中实线和虚线分别为带压缩角的中性曲线和平板的中性曲线，计算方法同2.2节扩张角。由图可知，与扩张角类似，压缩角对第一模态中线曲线的下支影响也很小，原因如2.4节所述。上支则同扩张角相反，压缩角使其向上偏折，即不稳定波的频率范围变大，偏折程度随压缩角的增大而增大。

选取频率为0.65的扰动波，分别采用直接数值模拟（DNS）和流动稳定性理论（LST）方法计算扰动过压缩角为1°、2°、3°的幅值演化。图10（d～f）给出了频率ω＝0.65的扰动波的幅值演化曲线。其中，实线代表数值模拟结果，虚线代表流动稳定性的计算结果。由图可知，三幅图中DNS和LST所计算的扰动幅值增长趋势一致，与中性曲线的预测结果吻合。图10（g～i）分别为压缩角1°、2°、3°的修正系数曲线。由图可知，在同一频率下，修正系数随压缩角的不同而不同，修正量范围为－0.085～0.025，修正系数很小。

同扩张角类似，压缩角对第一模态扰动波也产生了幅值调制，如图10（d）所示。其原因如前2.4节所述。由图10（d）、（e）、（f）可得，对于同一频率的扰动波，扰动幅值的调制随角度的增大而减弱，这与扩张角正好相反。这是由于过压缩角后，中性曲线上支向上偏折严重，进而使得增长率增大，从而导致其幅值远大于其他波数的波，调制现象减弱，不影响扰动总的增长或衰减趋势。

由图10（a～c）可知，第一模态扰动波过压缩角后，不稳定波频率范围变大，即原来稳定的高频扰动波变成不稳定状态。在此工况下，采用eN方法计算N值预测转捩时，如果考虑第一模态扰动波的影响，需要对N值进行修正。

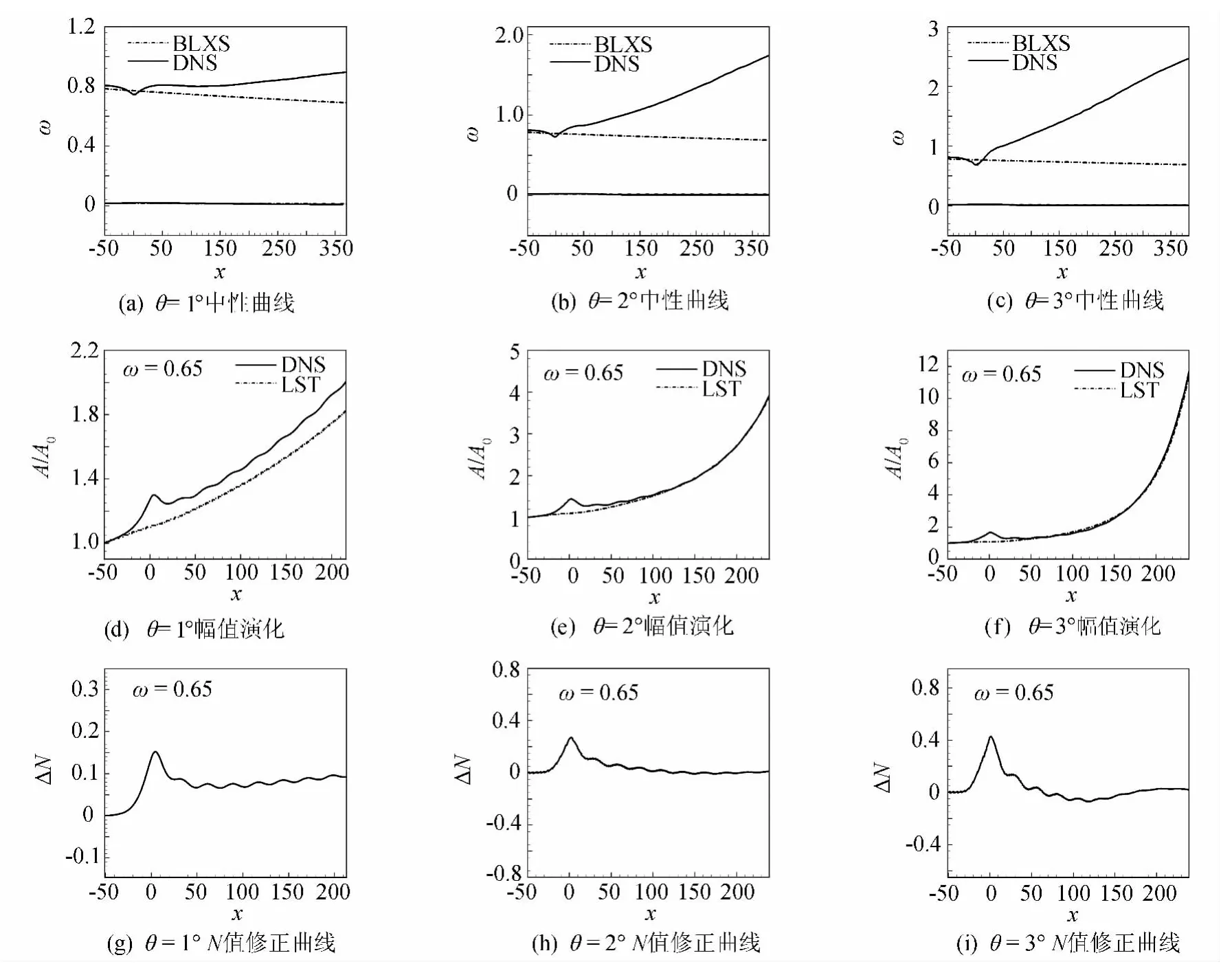
图10 压缩角为1°，2°，3°第一模态扰动波中性曲线和幅值演化Fig.10 Neutral curves in first mode and the curves of amplitude evolution（θ＝1°，2°，3°）

3 结 论

本文采用数值模拟结合线性稳定性分析的方法对折角分别为±1°，±2°，±3°（正为压缩角、负为扩张角）的高超声速边界层中扰动波的线性演化进行了初步研究，分别考虑扩张角和压缩角对第一模态和第二模态扰动波的影响。同时，对采用eN方法计算带有小折角工况下的N 值进行验证分析，提出当存在小折角时，需要对N值修正的概念，并对具体的工况给出了修正系数。通过计算分析，所得结论如下：

（1）扩张角对第一模态和第二模态扰动波具有阻断作用。第二模态中性曲线过扩张角后向下偏折，偏折程度随扩张角的增大而增大。当扩张角为1°时，中性曲线偏折较小，扩张角前的不稳定波具有足够的增长区间。在本文所计算的工况下，频率为1.92的扰动波采用eN方法时需要对N 值进行修正，修正系数为－0.2。当扩张角为2°、3°时，由于中性曲线偏折严重，不需要对N值进行修正，可以采用常规eN方法计算N值。

（2）扩张角对第一模态的中性曲线下支影响很小，这是由于靠近壁面附近的速度剖面过扩张角时变化很小。中性曲线的上支在扩张角后向下偏折，程度随扩张角的增大而增大。当扩张角为3°时，在扩张角下游产生中性曲线间断的现象。由于不稳定扰动波过扩张角后全部衰减，采用eN方法时不需要对N值进行修正。

（3）同扩张角相反，第二模态的中性曲线过压缩角后向上偏折，程度随压缩角的增大而增大。当压缩角为1°时，中性曲线向上偏折较小，压缩角前的不稳定波具有有效的增长区间。在本文所计算的工况下，当采用eN方法计算带压缩角的流场时，需要对N值进行修正，修正范围为－0.6～0.6。当压缩角为2°、3°时，中性曲线向上偏折更加严重，甚至出现中性曲线间断的现象，不需要对N值进行修正，可以采用常规eN方法进行计算。

（4）压缩角对第一模态中性曲线的下支影响很小，这与扩张角所得结论一致。但是其上支与扩张角相反，在压缩角后向上偏折，程度随压缩角的增大而增大。即不稳定波的频率范围增大，所以当考虑计算第一模态的N值时，需要对其进行适当修正。

（5）计算发现第一模态扰动波通过折角演化时出现幅值调制现象，这是由于扰动波通过折角时，激发出不同波数的扰动波相互叠加所导致的。但是调制所引起的幅值变化很小，不影响扰动总的增长或衰减趋势。

［1］SU C H，ZHOU H.Transition prediction of a hypersonic boundary layer over a cone at small angle of attack with the improvement ofmethod［J］.Science in China Series，2009，52（1）：115－123.

［2］GNOFFO P A.CFD validation studies for hypersonic flow prediction［R］.NASA Langley Research Center Hampton，2001，VA 23681－0001.

［2］MASON W H.Fundamental issues in subsonic transonic expansion corner aerodynamics［R］.AIAA 93－0649.

［4］SMITH F T，MERKIN J H.Triple－deck solutions for subsonic flow past humps，steps，concave or convex corners and wedged trailing edge［J］.Computer and Fluids，1982，10（1）：7－25.

［5］VERHOFF A，STOOKESBERRY D，MICHAL T.Hodograph solution for compressible low past a corner and comparison with Euler numerical predictions［R］.AIAA 1991：91－1547.http：／／arc.aiaa.org／doi／abs／10.2514／6.1991－1547.

［6］CHEW Y T，SQUIRE L C.The boundary layer development downstream of a shock interaction at an expansion corner［C］.Reports and Memoranda，No.3839，1978.

［7］LIU J X，LUO J S.Effect of disturbances at inlet on hypersonic boundary layer transition on a blunt cone at small angle of attack［J］.Applied Mathematics and Mechanics，2010，31（5）：505－515.（in Chinese）刘建新，罗纪生.小攻角高超声速钝锥边界层中不同扰动对转捩的影响［J］.应用数学和力学，2010，31（5）：505－515.

［8］ANDERSON J D.Computational fluid dynamics［M］.北京：机械工业出版社，2007.

［9］周恒，赵耕夫.流动稳定性［M］.北京：国防工业出版社，2004.

［10］MACK L M.Boundary－layer linear stability theory［R］.AGARD Report，1984，No.709.

［11］朱幼兰，钟锡昌，陈炳木，等.初边值问题差分方法及绕流，纯粹数学与应用数学专著［M］.北京：科学出版社，1980：424－452.

［12］HERBERT T H，ESFAHANIAN V.Stability of hypersonic flow over a blunt body［R］.AGARD CP 514，1993，28：1－12.

［13］ZHONG X L，MA Y B.Boundary－layer receptivity of Mach 7.99flow over a blunt cone to free－stream acoustic waves［J］.Journal of Fluid Mechanics，2006，556：55－103.

［14］MALIK M R，BALAKUMAR P.Instability and transition in three－dimensional supersonic boundary layers［C］.4th.AIAA International Aerospace Planes Conference 4th，Orlando，FL，1992.

［15］MACK L M.Stability of three dimensional boundary layers on swept wings at transonic speeds［R］／／Proc.IUTAM Symposium III［C］.Springer，Gottingen，1988.