典型桥梁断面风致振动的气动能量特征分析

刘祖军，杨詠昕，周冰凌

（1.华北水利水电大学 土木与交通学院，河南 郑州 450045；2.同济大学 桥梁工程系，上海 200092；3.四川蜀泰建筑设计有限公司，四川 成都 610000）

0 引 言

颤振属于自激振动，其物理机理可以从能量的角度加以深入的阐释。处于气流中的桥梁其能量反馈机制表现为气流输入到结构—气流系统中的能量与结构阻尼耗散能量之间的平衡关系，当输入到结构—气流系统中的能量小于结构阻尼耗能时时，结构在初始扰动下将作衰减（阻尼）振动；而当输入的能量大于结构阻尼耗能时结构在初始扰动下将作发散振动；两者相等时结构在初始扰动下将作等幅简谐振动。

在桥梁自激振动能量分析方面各国学者也进行了尝试，Scanlan［1］最早建立了桥梁颤振的多模态分析方法，并从能量的观点对桥梁的颤振稳定性进行了很有价值的研究，给出了在一个振动周期内气流沿桥梁断面每延米输入的总能量和结构耗能的表达式，但他仅给出了一个理论框架，如何从能量的角度对桥梁进行颤振分析，没有给出具体的方法。

Larsen以CFD方法为基础，根据离散涡计算中涡旋的运动规律提出了一个简化分析模型［2］。这个模型描述了在桥梁断面扭转运动的一个周期里涡旋的运动情况，并通过积分估算由涡旋产生的气动力对桥梁断面所做的总功，通过用能量方法分析涡激力做攻与结构稳定之间的关系。Larsen的研究具有很好的开创性，但是他的计算模型假定在旋涡沿横截面移动时，旋涡升力保持不变并且结构阻尼为零，这和实际情况有很大的不同。

我国的刘高博士从结构与气流系统内部能量平衡的观点对系统的颤振进行研究［3］，发展了一种全桥多模态颤振分析方法－能量法，通过建立系统等效阻尼比与系统能量变化率之间的关系，推演了系统以及各阶模态等效阻尼比的计算方法，并根据不同风速下系统能量变化率来判断系统的颤振稳定性。但这种方法不能很好的分析气流与结构之间的细观作用，特别是结构自激振动中系统能量的分布和转化情况。同济大学博士杨詠昕、刘祖军基于分步分析的方法从能量角度对典型桥梁断面颤振的机理进行了研究［4］。

在航空方面机翼的气动弹性力学研究中，Frazer早在1939年就分析了维持机翼强迫振动所需要的能量条件［5］，Nissim在20世纪70年代提出了气动能量概念作为对机翼主动控制的理论基础［6］，Jones分析了颤振发生的能量特征，上述工作构成机翼的气动弹性力学研究应用的基础［7］。在机械领域的叶轮机气动弹性力学研究中Carta提出了用于颤振失稳预测的能量稳定判据［8］。后来Klose和Heinig通过研究证明能量法用于颤振失稳的预测可被认为是特征值法在叶片高质量比下的特殊应用，并指出应用能量法预测的一些失效情况［9］。

本文通过风洞试验研究了单箱的颤振性能，基于流固松耦合的计算策略，利用现有流体软件的用户自定义（UDF）功能，应用CFD数值方法，模拟了单箱颤振过程，根据分块分析的思想研究了颤振过程中振动模型表面不同区域吸收气流能量的特点，并分析了旋涡的非定常演化对模型表面不同区域压力特性的影响。

1 单箱风洞测振试验及结果分析

风洞试验在同济大学土木工程防灾国家重点实验室TJ－4边界层风洞中进行，该风洞为低速回流式风洞，测振的试验段尺寸为：宽0.814m，高0.8m，长2.0m，设计最大试验风速为30m／s。单箱断面依据大海带东桥的主桥断面为原型进行缩尺，其截面尺寸如图1所示，纵向长度0.8m，采用铝质芯棒，外覆泡沫制成。

图1 单箱模型 （单位：mm）Fig.1 The model of box（unit：mm）

模型的基本参数如下：m＝1.3625kg／m，Im＝0.01277kg·m，竖向频率fh＝2.825Hz，扭转频率fa＝7.451Hz。测振时采用激光位移计记录模型试验风速下的位移信号。

当风速小于18m／s时结构的竖向位移振幅很小，但是存在较小幅度的扭转振动。当风速超过18m／s后结构振动位移极大值和方差就突然增大，竖向振动的参与程度也不断增加，直到风速到达20.8m／s时结构出现了颤振失稳现象。图2和图3给出了颤振临界风速下的位移时程曲线。

2 颤振过程的数值模拟

2.1 单箱颤振数值模拟方法

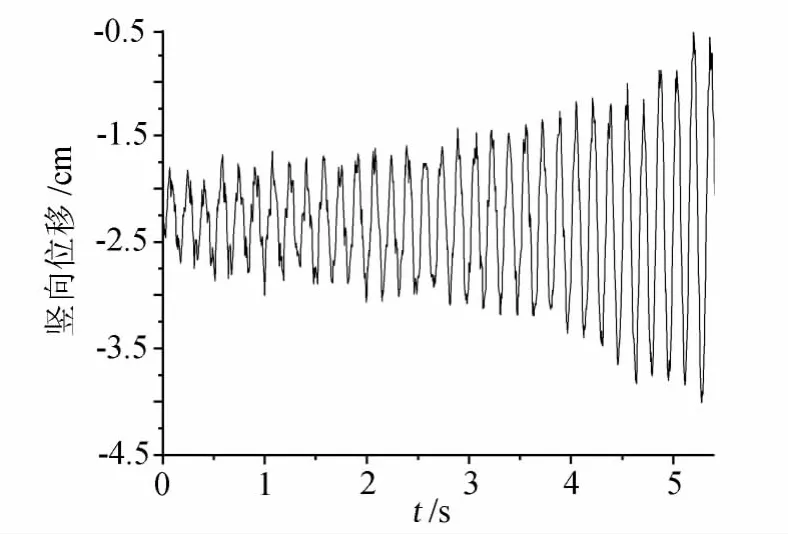
图2 竖向振动位移时程响应 （20.8m／s）Fig.2 Vertical vibration displacement vs.time curve of box section（20.8m／s）

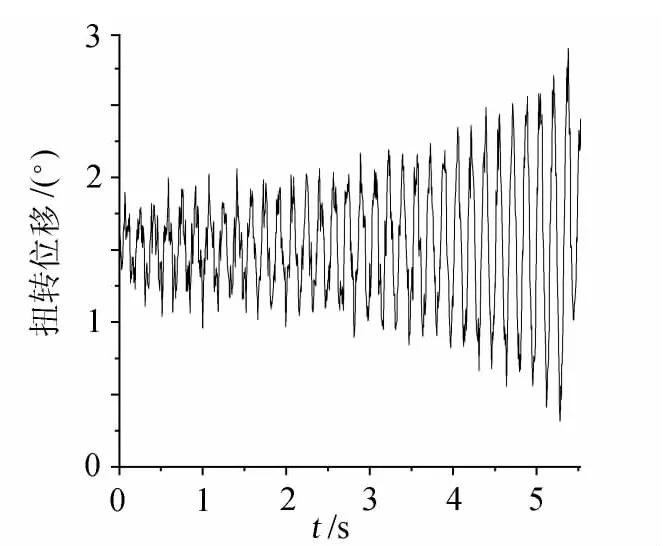
图3 扭转振动位移时程响应（20.8m／s）Fig.3 Torsional vibration displacement vs.time curve of box section（20.8m／s）

桥梁颤振发散是流体与结构相互动力作用的结果。处理流固耦合的问题可以采用强耦合和松耦合这两种方法。强耦合求解方法是以求解流体运动的迭代过程为主，将物体运动的求解耦合在流体运动求解过程中.松耦合方法在每一个时间步内分别对流体和结构依次求解，然后通过中间平台交换数据信息，从而实现两个场的耦合求解。这种方法对计算机硬件的要求不高，并且可以充分发挥CFD（Computational Fluid Dynamics）计算和CSD（Computational Structural Dynamics）计算的各自优点，能实现数值计算的模块化。在分析桥梁结构风致振动问题时多采用松耦合的计算策略。

本文采用松耦合的计算方法，利用现有商业软件Fluent提供的基于ALE（Arbitrary Lagrange Euler）方法的动网格技术，来实现颤振的数值模拟，通过软件的用户自定义函数描述模型及周围气流的刚体运动，具体的计算流程图如图4所示。

图4 颤振数值模拟流程图Fig.4 The process of flutter numerical simulation

颤振数值模拟过程的具体步骤为：

（1）首先进行流体域内固定断面的非定常绕流计算，将计算获得的三分力系数通过Fluent软件的用户自定义功能输出到指定的文本中，然后再将其换算为作用在模型表面上的升力和升力矩，从而获取t时刻的气动力。

（2）根据计算所获得的升力和升力矩，通过数值方法对振动结构进行结 构动力学求解。根据newmark－β方法求解竖向和扭转振动方程，获得t＋Δt时刻结构运动的竖向速度和扭转速度。

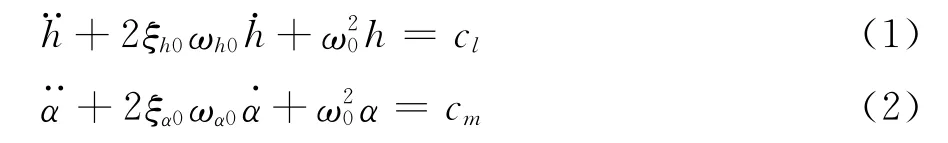
（3）将模型振动的速度赋值给包围模型断面并随模型一起做刚体运动的部分流体区域，通过Fluent提供的用法自定以函数（UDF）描述模型及周围流体的运动，采用动网格方法进行流体域的求解，获得振动断面的气动升力和升力矩。

（4）重复（2）－（3）步，获得桥梁断面振动响应的时程。

（5）根据断面的响应时程曲线判断振动是否已经发散，如果已经发散则该风速即为颤振临界风速，否则增加风速按照（1）－（4）步重新计算直到达到振动发散。

2.2 颤振数值模拟结果分析

数值模拟时采用商业软件Fluent提供的RANS方法的k－ωSST两方程模型［10－11］，计算域的大小参考了同济大学土木工程防灾国家重点试验室TJ－4风洞的中段试验端设置，计算域沿流线长度为3m（其中上游1m，下游2m），横向宽度为0.8m。计算时壁面附近最小网格尺度为0.0004m，计算域采用分块结构化网格。网格数量为15.6万。

计算参数设置为：动量，湍动能和能量耗散均采用两阶迎风格式进行离散，压力速度耦合采用SIMPLE算法，求解器采用分离式，计算模式选用两阶隐式。边界条件的设定为：速度入口，入口初始风速15m／s，湍流强度0.5%，压力出口，计算域的上端和下端设为对称边界条件，表面采用无滑移的壁面条件。

由于RANS方法平均的结果是将流场时空变化的细节一概抹平，丢失了流场脉动运动中的大量信息，并且为了使N－S方程封闭，提出了Reynolds应力模型和涡粘模型12－14］，这些模型存在着对经验数据过分依赖和预报精度相对较低的局限性。

由于受到计算机硬件条件的限制，本文仍然采用了RANS方法模拟箱梁颤振过程，并提取了模型表面压力进行能量分析，需要说明的是计算获得压力是平均后的结果，因此本文计算的能量可以反映结构振动过程中的总体变化规律，但忽略了瞬时脉动压力对结构振动能量的贡献。

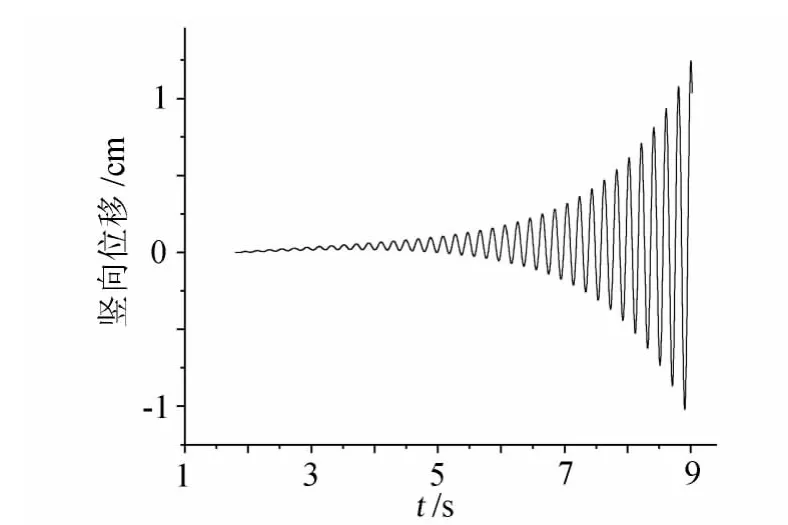
图5 竖向振动位移时程响应 （20.8m／s，CFD数值模拟）Fig.5 Vertical vibration displacement vs time curve of box section（20.8m／s，CFD）

该箱梁的颤振临界风速为20.8m／s。图5、图6是平板颤振时刻的位移时程，数值模拟所获的颤振频率为4.92Hz，实测颤振频率为4.59Hz。

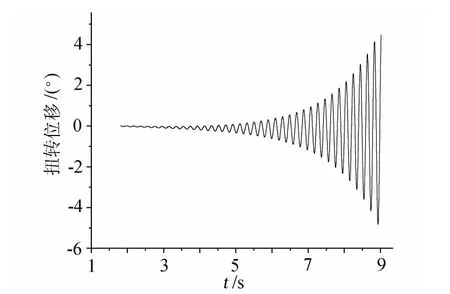
图6 扭转振动位移时程响应（20.8m／s，CFD数值模拟）Fig.6 Torsional vibration displacement vs time curve of box section（20.8m／s，CFD）

3 基于分块分析思路的颤振过程能量分析

3.1 分块分析能量计算方法

分块分析主要是为了比较详细的捕捉表面压力的变化，寻找引起颤振发散的主要的能量输入特点，同时能够考虑尾部旋涡对气流能量输入方式的影响和影响范围。根据对断面进行分区，然后按照下式分别计算不同区域的能量输入特点.单位区域的能量计算公式如下：

单位面积上一个周期内气动力输入到系统的能量w：

则面积为S（图7的网格线部分）的区域气动力输入的能量w（s，t）：

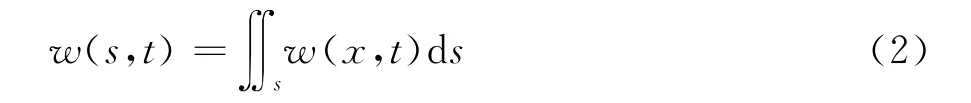
P（x，t）为结构表面的压力，v（x，t）为结构运动速度，n（x，t）为压力与速度之间的夹角。

图7 分块分析示意图Fig.7 The Block Analysis

根据本文提出的分块分析思路，编制了相应的计算程序，通过提取数值计算获得的模型表面压力，详细的研究了在一个周期内气流向结构输送能量的过程，模型表面进行了如图8所示的分区。

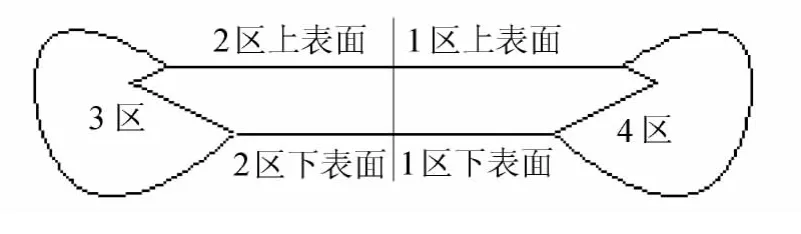
图8 模型表面分区Fig.8 The partition of the model

图9～图14是模型扭转振动时不同分区输入到系统的能量。第1个区域在前半个周期内上表面消耗能量，下表面吸入能量，后半个周期则反之。一个完整周期内输入到系统的能量为正，但数值较小。上下表面输入到系统能量具有较好的周期性特征，具体如图9所示。第4个区域的输入系统的能量特点和1区基本相似，能量的输入也具有周期性的特点，二者的不同之处在于第4个区域是消耗系统的能量。第4区域受到尾部旋涡的直接作用。而尾部旋涡运动具有一定的规律性，并且尾端风嘴处上下侧交替出现的旋涡聚集了较大的能量，控制了模型尾端的自由振动，使得模型尾端的运动和尾部旋涡的运动趋势基本同步，因此造成了该区域气流输入能量具有明显的周期性（图15）。

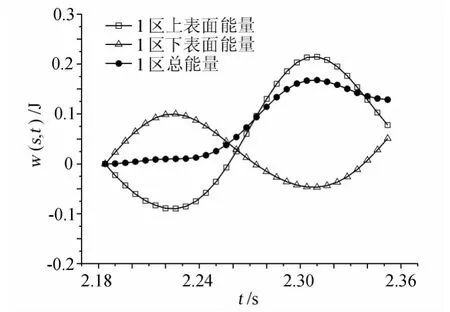
图9 1区扭转运动的能量随时间变化关系Fig.9 The energy of torsion in the first partition vs.time curve

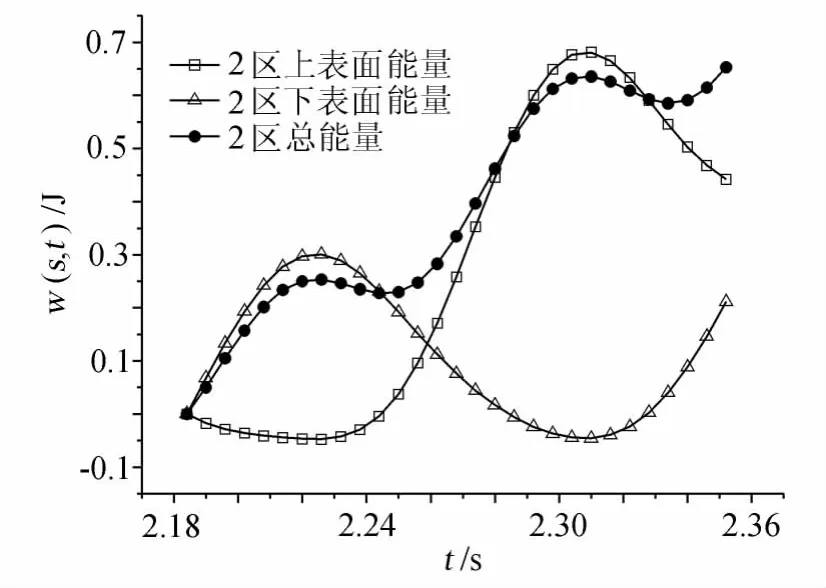
图10 2区扭转运动的能量随时间变化关系Fig.10 The energy of torsion in the second partition vs.time curve

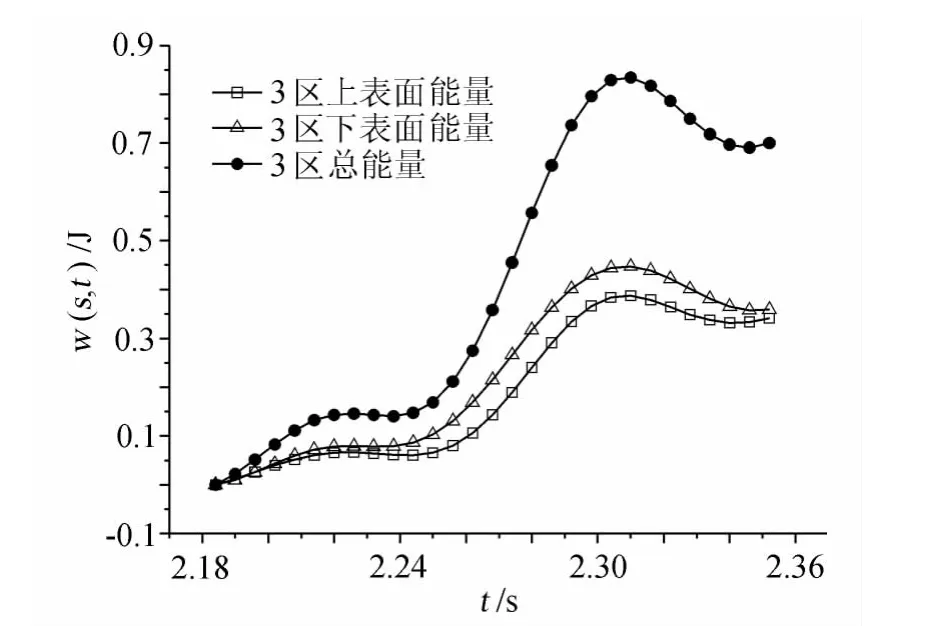
图11 3区扭转运动的能量随时间变化关系Fig.11 The energy of torsion in the third partition vs.time curve

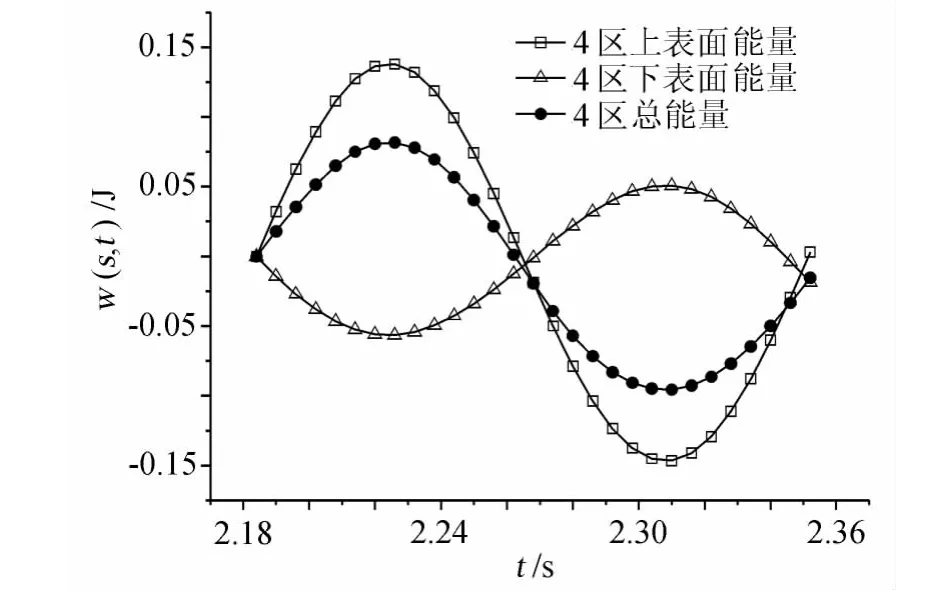
图12 4区扭转运动的能量随时间变化关系Fig.12 The energy of torsion in the fourth partition vs.time curve

图13 各分区扭转振动能量随时间变化关系Fig.13 The energy of torsion in every partition vs.time curve

第2个区域为系统提供了较多的能量，在整个振动过程中上表面在前1／4周期消耗能量，后3／4周期内吸入能量，下表面的情况与之相反，总能量为正，数值较大，且增加较快，如图10。第3个区域也就是风嘴部位是扭转系统的主要能量来源，在一个完整周期内上下表面均吸入系统能量并且数值较大（图11）。因此在颤振过程中模型的主要吸能部位分布在迎风端风嘴及其附近的区域。从第23个区域的能量随时间的变化关系曲线上可以看出这两个部位的能量输入的周期性不明显，受尾部旋涡运动的影响较小。

各分区对扭转振动的能量贡献如图13所示，从单箱扭转振动主要能量输入曲线可以发现气流输入到单箱的主要能量在一个周期内是不断增加的，所以单箱的颤振多为突然性失稳。竖向振动的主要能量输入则是主要由第2个区域引起，具体如图14。上述分析表明单箱颤振时扭转能量的主要吸入部分是迎风端的风嘴和靠近风嘴附近的区域如图15所示。

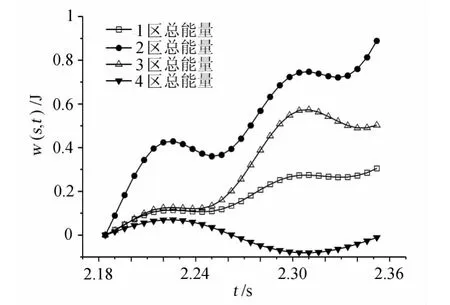
图14 各分区竖向振动能量随时间变化关系Fig.14 The energy of vertical in every partition vs.time curve

图15 气流能量输入图Fig.15 The energy input by air

3.2 颤振过程旋涡演化对模型不同区域压力特性的影响

通过CFD数值方法模拟了单箱处于颤振临界状态的绕流特征。由于振动模型周围的流场是千变万花的，即使模型振动到同一位置时，其周围对应的流场也完全不同，因此采用了相位平均的方法［15］探讨了单箱尾部风嘴处的旋涡的演化规律。

从流场的相位平均的分析结果（图16）可以看出箱梁振动过程中尾部风嘴处的旋涡存在这样的演化过程：当结构处于平衡位置时，在风嘴下侧存在回流区，将要形成旋涡；当结构由平衡位置振动到负最大位移时在风嘴的上下侧同时存在旋涡，但是上侧旋涡尺度较小，下部旋涡尺度很大，结构处于下旋涡的控制下；随后结构负最大位移回复到平衡位置时，上侧旋涡消失，下部旋涡的尺度减小，由平衡位置振动到正最大位移时，在在风嘴的上下侧又产生了一对尺度较大，接近椭圆形的旋涡，结构处于上下旋涡的共同控制下。

图16 单箱断面的旋涡驱动结构运动的流（颤振风速20.8m／s，数值模拟）Fig.16 Vortex driven structural movement of box section（20.8m／s，CFD ）

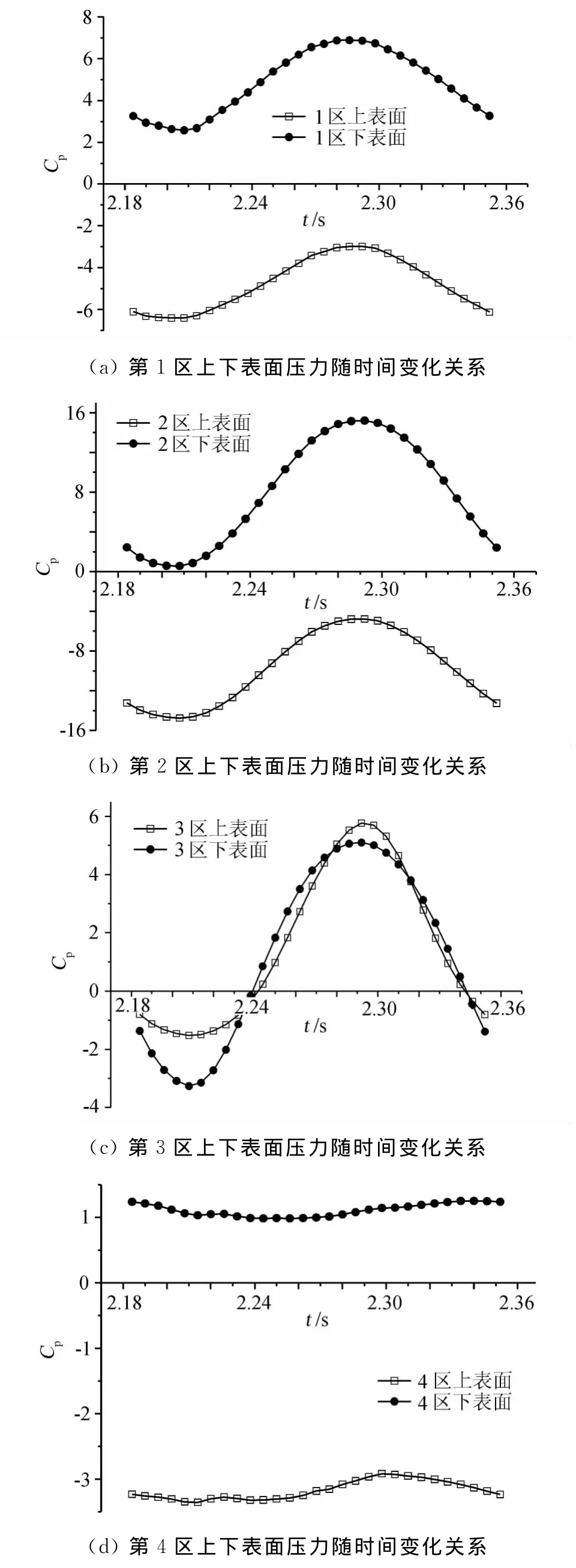
图17 箱梁表面4个分区上下表面压力随时间变化关系Fig.17 Four regional of box girder surface pressure versus time

从4个区域输入到系统扭转振动的能量随时间的变化关系，我们可以推测出尾部旋涡对气流输入到系统能量的影响。模型尾端风嘴附近的区域受到旋涡的直接作用，输入到系统的能量具有很明显的周期性特点。图17给出了4个区域上下表面压力分布随时间的变化关系。为了清楚说明尾部旋涡对模型不同部位的影响定义了上下表面压力差的相对变化量：＝（Cpu－Cpd）／Cpu，其中Cpu、Cpd为模型上下表面最大压力。第4个区域的（4）＝4.28（1）＝1.43（2）＝1.31，（3）＝0（图18），因此可以看出越靠近尾流区域，上下表面压力差值的相对值越大，第4区域最大，而距尾流区最远的3区上下表面之间的压力相对差很小，两个曲线基本重合。从流场机制上说箱梁尾部风嘴附近受到旋涡的直接推动作用，其表面压力的变化特点与旋涡的运动规律很接近，具有明显的周期性。尾部风嘴上下侧的旋涡交替控制结构的运动，因此造成尾部风嘴区域的上下表面的压力相对波动较大，而远离尾流的区域受此影响较小，其上下表面的压力波动的程度相对较小。

图18 箱梁表面4个分区上下表面相对压力差的波动系数Fig.18 The volatility coefficient of relative pressure difference on the four model surface regional

4 结 论

本文通过风洞试验测试了单箱的颤振性能，采用CFD数值计算方法，并基于流固松耦合的计算策略模拟了单箱的颤振过程，结合分块分析的思路定量研究气流对振动模型表面不同区域的能量输入特点及其对模型不同部位表面压力的影响。通过上述研究得出以下几点结论：

（1）分块分析的计算结果表明迎风端的风嘴及其附近区是扭转振动能量的主要输入部位，对系统的振动的稳定性起重要作用。

（2）从模型表面不同区域的能量输入特点可以发现由于模型尾部风嘴附近上下侧的旋涡交替作用具有明显的规律性，因此造成模型靠近尾流区域的气流能量输入方式具有较明显的周期性，而模型迎风端的气流输入规律性较差，周期性不明显。

（3）分块分析结果表明由于箱梁尾部风嘴上下侧的旋涡交替作用对结构振动的影响很大，从而造成了尾部风嘴区域的上下表面压力相对波动较大。而远离尾部旋涡的模型区域受旋涡交替作用影响较小，因此使得该模型区域上下表面的压力波动的程度相对较小。

（4）CFD数值模拟的结果表明单箱颤振过程中模型的周期性振动与模型尾部风嘴附近的上下侧旋涡的交替作用存在着一定的联系。

［1］SCANLAN R H.The action of flexible bridges under wind，I：flutter theory［J］.J of Sound and Vibration，1978，60（2）：187－199.

［2］LARSEN A.Aerodynamics of the Tacoma narrows bridgc－60years later［J］.Joumd of Structural Engineering International，2000，（10）：243.

［3］LIU Gao，WANG Xiuwei，QIANG Shizhong，et al.Flutter analysis of long－span suspension bridges by energy method［J］.China Journal of Highway and Transport，2000，12（3）：20－24.（in Chinese）刘高，王秀伟，强士中，等.大跨度悬索桥颤振分析的能量法［J］.中国公路学报，2000，12（3）：20－24.

［4］LIU Zujun，GE Yaojun，YANG Yongxin.Energy transformation mechanism of coupled bending－torsional flutter［J］.Jouranl of Tongji University（Natural Science），2011，39（7）：949－954.（in Chinese）刘祖高，葛耀君，杨詠昕.弯扭耦合颤振过程中的能量转换机理［J］.同济大学学报（自然科学版），2011，39（7）：949－954.

［5］FRAZER R A.On the power input required to maintain forced oscillations of an aeroplane wing in flight［J］.ARCR＆M，1939.

［6］NISSIM E.Flutter suppression using activecontrols based on the concept of aerodynamic energy［R］.NASATND 6199，1997.

［7］JONES J G.On the energy characteristics of the aerodynamic matrix and the relationship to possible flutter［J］.The Aeronautical Quqrterly，1983，3：212－225.

［8］CARTA F O.Coupled blade－disk－shroud flutter instabilities in turbojet engine rotors［J］.Journal of Engineering for Power，1967：419－426.

［9］KLOSE A，HEINIG K.A comparison of flutter calculations based on Eigenvalue and energy method［R］.AD－A2119741，1989.

［10］LUBCKE H，SCHMIDT S，RUNG T，et al.Comparison of les and rans in bluff－body flows［J］.Journal of Wind Engineering and Industrial Aerodynamics，2001，89（14－15）：1474－1485.

［11］TETSURO TAMURA，YOSHIYUKI ONO.LES analysis on aeroelastic instability of prisms in turbulent flow［J］.Journal of WInd Engineering and Industrial Aerodynamics，2003，（91）：51－64.

［12］LIU Zujun，GE Yaojun，YANG Yongxin.Identification of aerodynamic parameters of a flat plate with multimoving grid technique based on large eddy simulation［J］.Journal of Vibration and Shock，2011，30（4）：156－160.（in Chinese）刘祖军，葛耀君，杨詠昕.基于大涡模拟方法的多层动网格技术识别平板气动参数［J］.振动与冲击，2011，30（4）：156－160.

［13］ZHOU Zhiyong，YANG Likun.Numerical study on the mechanism of torsional flutter forΠ－shaped section［J］.Acta Aerodynamics Sinica，2009，27（6）：683－689.（in Chinese周志勇，杨立坤.Π形板梁分离流扭转颤振机理数值研究［J］.空气动力学学报，2009，27（6）：683－689.

［14］ZHOU Zhiyong.Numerical simulation study on Reynolds number effect on bridge decks［J］.Acta Aerodynamics Sinica，2009，27（6）：664－670.（in Chinese）周志勇.桥梁断面雷诺数效应数值模拟研究［J］.空气动力学学报，2009，27（6）：664－670.

［15］FUJISAWA N，TAKEDA G，IKE N.Phase－averaged characteristics of flow around a circular cylinder under acoustic excitation control［J］.Journal of Fluids and Structures，2004，19：159－170.