市场微观结构噪声的形成机制研究

刘威仪

（北京大学 光华管理学院，北京 100871）

市场微观结构噪声的形成机制研究

刘威仪

（北京大学 光华管理学院，北京 100871）

模拟结果和实证分析表明，三种形成机制下的微观结构噪声具有不同类别的统计特征，其噪声序列分别表现为白噪声、自相关以及与价格序列的相关性，涵盖了噪声假设的各个类别。除此之外，价格离散和非频繁交易还是“零收益率”这种特殊噪声现象的产生原因，其中价格离散对低价格资产的影响更为严重，这是我国金融市场中最常见的噪声形成机制之一。

市场微观结构噪声；买卖价差；价格离散；非频繁交易；零收益率

一、引言

市场微观结构（Market Microstructure）理论是金融市场学研究的一个重要分支。自从Black(1986)[1]提出噪声（Noise）的概念以来，人们对市场微观结构下金融资产的价格发现和定价机制展开了新角度的研究，这些成果主要展现在Madhavan(2000)[2]、O’Hara(1995)[3]、Stoll(2003)[4]和 Hasbrouck(2007)[5]。近年来，金融高频数据的广泛普及拓宽了市场微观结构理论的应用范围，特别是微观结构噪声在高频观测下带来的严重问题日益受到重视，因此关于噪声的研究再次成为金融计量领域关注的热点。

对于市场微观结构噪声形成机制的研究，主要集中在早期文献基于日度低频信息对价格形成机制的刻画。已有文献表明，市场微观结构噪声是由交易成本和交易摩擦共同作用形成的，这些因素主要包括：买卖价差（bid-ask spread）、价格离散（price discreteness）和非频繁交易（infrequent trading）等。其中，买卖价差也可以作为流动性的度量方式之一，相关研究较为全面和广泛；而离散价格和非频繁交易反映了“零收益率”（zero returns）①“零收益率”（zero returns）又称为“刚性交易”（flat trading），即资产价格在一定时间段内保持不变的现象。可以参考Delattre和Jacod(1997),Lesmond etal.(1999),以及Phillips和Yu(2008)的研究。这种特殊的实证表现，是另一种刻画噪声和流动性的重要方式。

Zhang etal.(2005)的研究表明，随着观测频率的增加，传统的波动率估计将受到微观结构噪声的主导而偏离真实，即高频数据信息实际上放大了噪声的影响，导致传统的金融计量方法不能满足实际的情况。因此，近几年来对市场微观结构噪声的研究更强调于高频数据下的降噪方法，特别是针对波动率估计和价格跳跃检验的研究。这类文献并不深究噪声的形成因素，而是直接假设其为白噪声序列或平稳序列进行处理。

已有文献对市场微观结构的价格形成机制和噪声的微观计量的研究是分离的，前者侧重于低频数据和流动性理论的研究，而后者侧重于高频数据和统计方法的研究。本文在此基础上，主要的研究体现在以下几个方面：（1）寻求上述两个方向的结合点，将价格形成机制的研究转化为噪声形成机制的理论，并将其统一为高频数据的模型框架系统地展现出来；（2）利用蒙特卡罗模拟探索噪声的形成机制与其统计特征的内在联系，并基于此进一步分析已有文献关于市场微观结构噪声假设的合理性；（3）根据以上的方法和结论给出实证分析设计，揭示中国股票市场微观结构噪声的形成机制及影响特征。

二、微观结构噪声的一般理论框架

现实的金融市场常常偏离有效市场，交易成本和交易摩擦会影响资产价格的短期行为，使得观测的价格偏离真实的价格，这种偏离称为市场微观结构噪声。实际上，我们观测到的资产价格一般都是包含噪声的，因此可以将其分解成两个组成部分

其中pt表示观测的对数价格，表示真实的对数价格，εt称为市场微观结构噪声。

不失一般性，令t表示第t个交易日。将其划分为n个等距区间的离散采样，分别记为pit，i=0,1,2,…,n，于是每个小区间内对应的收益率为

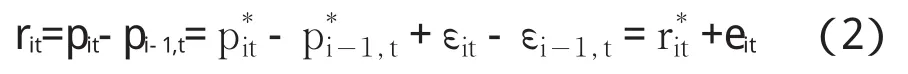
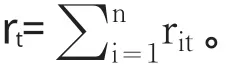
如果用收益率的二次变差或方差来刻画价格的变动程度，那么（2）式说明了真实对数价格pt的变动程度至少包含了真实对数价格和微观结构噪声εt的变动程度。前者对于资产定价和风险管理的理论和应用至关重要，后者则能够反映市场微观结构特征与市场参与者的行为，在微观层次上揭示金融市场的运作机制。因此，很有必要将上述二者进行分解研究。

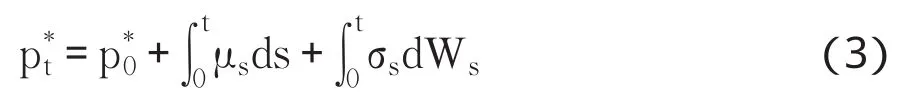
其中{μt}t≥0是漂移过程，{σt}t≥0是扩散过程，{Wt}t≥0为标准布朗运动过程。

对于微观结构噪声过程{εt}，最常见的假设是认为其服从独立同分布的白噪声过程（Zhang etal.,2005;Bandi和Russel,2006[6）]，具体为

（a）εit的均值为0，方差有限；

（b）εit是独立同分布（i.i.d.）的随机变量序列；

（c）εit与相互独立，对任意的i和j成立。

在上述假设之下，由（2）式定义的观测价格收益率{}rt的自相关函数具有MA（1）结构，即

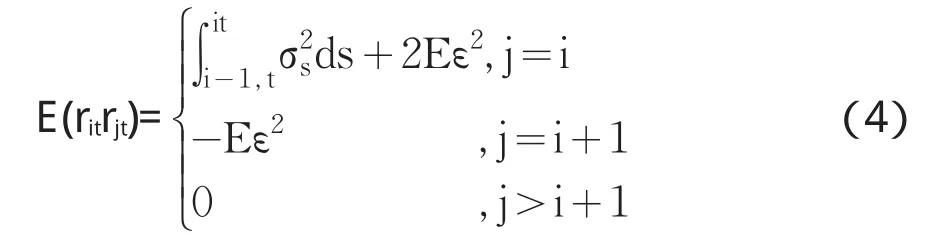
虽然绝大多数关于微观结构噪声的理论研究都是在上述假设下进行的，但是很多实证研究表明上述假设并不符合实际情况，因此Hansen和Lunde（2006）[7]以及A¨ It-Sahalia et al.(2010)等进一步假设噪声序列在一定时间内存在一阶或高阶自相关。例如，假设噪声序列{εt} 具有参数为 ρ(| ρ＜1|)的AR（1）结构，那么观测收益率序列的自相关函数满足

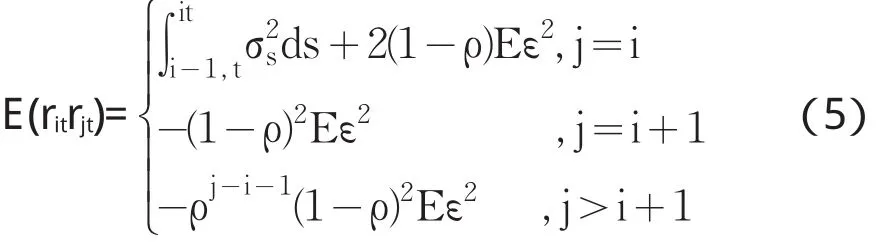
（5）式表明，如果噪声序列表现为很强的正相关，那么观测收益率序列的自相关函数将类似于白噪声序列的自相关函数，反而更接近于不存在噪声的情形。因此，对于噪声序列存在自相关的情形需要更加谨慎地处理。

除此之外，韩清和刘永刚（2007）[8]的研究表明，噪声序列不仅在一定时间内存在自相关，而且还与价格过程本身有关。这种情况可能产生更为多样的结果，相应的处理手段也更为复杂，因此目前涉及的文献相对较少。

本文并不对微观结构噪声进行直接假设，而是通过不同的噪声形成机制来考察相应的噪声分布状况和自相关结构，进而深入认识微观结构噪声假设的合理性，探索不同类别的噪声表现特征及其微观结构影响。

三、市场微观结构噪声的形成机制

微观结构噪声的一般理论框架是为了简化问题的一种抽象概括。由（1）式给出的噪声表达式虽然具有理论上的一般性，但并不能具体地反映某一种噪声的形成机制，因此难以进一步解释市场的微观结构特征。

微观结构噪声的形成机制是多样化的，这些因素包括但不限于：买卖价差、价格离散、非频繁交易、非同步交易、价格涨跌限制等。而本文主要关心当前研究中噪声形成机制模型化较为成熟的前面三种，并将传统的基于低频数据的噪声形成机制模型统一地扩展为基于高频数据的形式。

根据各类形成机制模型，可以利用蒙特卡罗模拟生成观测价格序列，进而产生相应机制下的微观结构噪声序列，其中真实价格序列由（2）式模拟得到①具体模拟参数采用与Goncalves和Meddahi(2006)相同的设置，即可以忽略漂移系数的影响μt=0，同时σt服从参数为(θ,ω,η)的GARCH(1,1)扩散过程，其中Bt是与（3）式中的Wt相互独立的布朗运动过程，(θ,ω,η)=(0.035,0.636,0.144)。。基于模拟的结果，可以进一步深入分析每种形成机制下微观结构噪声的统计特征和影响形式。

（一）买卖价差

买卖价差（bid-ask spread）指的是买入价和卖出价之间的差距，即投资者买入资产并立即卖出所需要付出的成本，因此买卖价差又是交易成本和流动性的一种度量方式。在有效市场上，价格过程理论上应该服从随机游走运动，然而交易成本的存在使得观测的价格偏离真实的价格，因此买卖价差是形成微观结构噪声最直接的因素之一。

Roll(1984)[9]给出的模型是最常见的买卖价差度量方式，他不仅提供了利用观测价格过程估计买卖价差的方法，还给出了观测价格、真实价格和买卖价差的三者之间的联系，因此与其他单纯的买卖价差估计量相比更有利于刻画微观结构噪声的形成过程。这里我们关心的是高频价格过程的微观结构噪声，可以将Roll(1984)[9]给出的基于日度低频数据的模型改写为如下高频的形式：

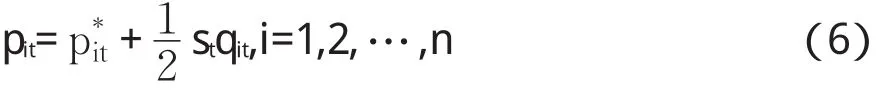
其中qit=1表示在买入价成交表示在卖出价成交。（6）式和Roll(1984)[9]的唯一区别是，Roll(1984)[9]认为买卖价差恒为常数，而（6）式只假定买卖价差在日内为常数。因此，利用日内的高频价格数据可以给出当日的买卖价差估计

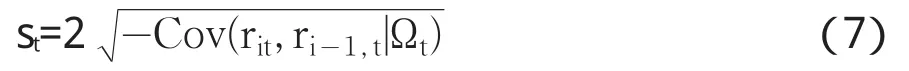
由于（6）式的初衷是给出流动性的刻画，因此它对噪声的刻画相对比较简单。具体来讲，（6）式是（1）式的一种特殊情况，由其形成的微观结构噪声是0.5stqit，因此是独立同分布的白噪声过程，满足(a)-(c)的假设条件。根据（4）式的结果，此时观测价格收益率{rt}的自相关函数应该具有MA(1)结构，具体模拟结果①此处给出的模拟设定是日内4个小时的分钟数据，且S0=10.00，s=0.1%。如图1所示。

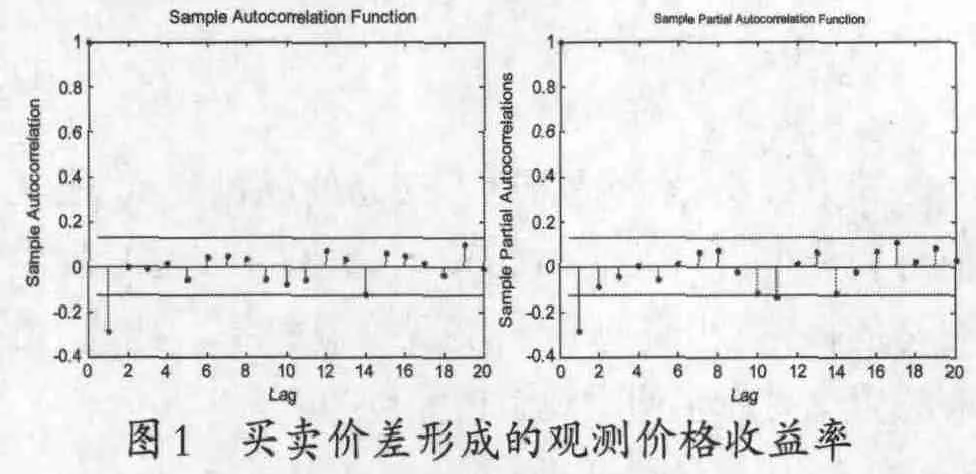
自相关函数图（左）和偏自相关函数图（右）

图1的结果表明观测价格收益率{rt}的自相关函数和偏自相关函数都具有一阶截尾性，即自相关函数具有MA（1）的结构，而偏自相关函数具有AR（1）的结构，因此整个过程并不能简单地用MA（1）模型来加以刻画。此外，当买卖价差较小时，观测收益率的自相关函数和偏自相关函数将退化为类似白噪声的结构。

总体而言，Roll(1984)[9]给出了一种形式上最为简单的买卖价差表达，由其形成的微观结构噪声也相对比较简单，满足(a)-(c)的假设条件。从流动性估计的角度来讲，Roll(1984)[9]虽然得到了比较广泛的运用，但仍然存在诸多不足，例如Holden(2009)指出在估计买卖价差时还需要考虑无交易和价格离散的情况。实际上，价格离散和非频繁交易不仅影响买卖价差的估计，也直接导致了其他形式的微观结构噪声的形成，我们将其作为另外的形成机制与买卖价差并列起来讨论。

（二）价格离散

价格离散（price discreteness）指的是资产报价的最小变动单位导致的价格变化的不连续性。目前国内外的绝大多数种类的金融资产采用十进制的报价形式，比如国内的股票市场和债券市场的资产价格最小变动单位为0.01元，又比如利率和汇率报价的最小变动单位分别为0.01和0.001；在国际上，也有采用分数报价机制的金融资产，比如美国股票市场在2001年以前采用1/4美元的最小变动单位，而美国债券市场则采用1/32美元的最小变动单位等。

直观地看，价格离散机制限制了买卖价差的幅度，进而影响了金融资产的波动性和流动性。从微观结构噪声的形成机制来讲，价格离散不仅通过影响买卖价差而形成噪声，而且直接地导致了观测价格的截断误差（round-offerror），使得观测价格偏离真实价格进而形成噪声。

Rosenbaum(2009)[10]和 Large(2011)认为截断误差是形成高频微观结构噪声最主要的原因之一，而由（1）式所给出的微观结构噪声却很难反映这种形成机制，因此他们采用了Delattre(1997)的价格离散模型：

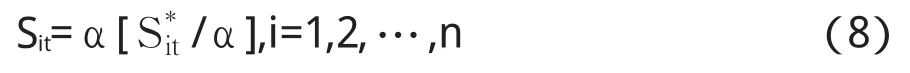
其中[·]是round取整函数，即四舍五入的取整形式，α是控制最小变动单位的参数，在大多数情况下α=0.01。此时，由价格离散导致的微观结构噪声为

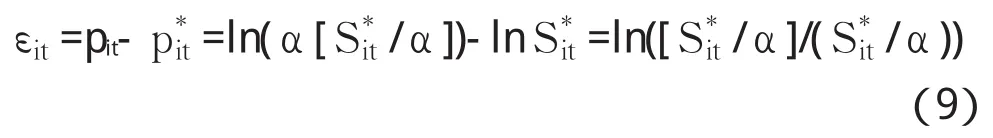
形式上（9）式给出的微观结构噪声与真实价格有关，但不难看出由于作商的关系噪声的大小与真实价格水平几乎无关，这同时也意味着噪声在较小的资产价格中占据更大的分量。图2给出了噪声及其分布的模拟图形②此处给出的模拟设定是日内4个小时的分钟数据，且S0=10.00，α=0.01。。

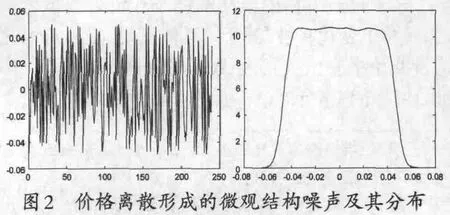
从图2的结果来看，由价格离散形成的微观结构噪声基本上分布在(-0.05,0.05]之间，形成“低峰薄尾”的分布状况。由于截断误差与价格水平有很大的关系，这里我们在固定价格最小变动幅度为0.01元的条件下，将初始价格分为1.00元至200.00元分别进行考察。具体模拟结果如表1所示。

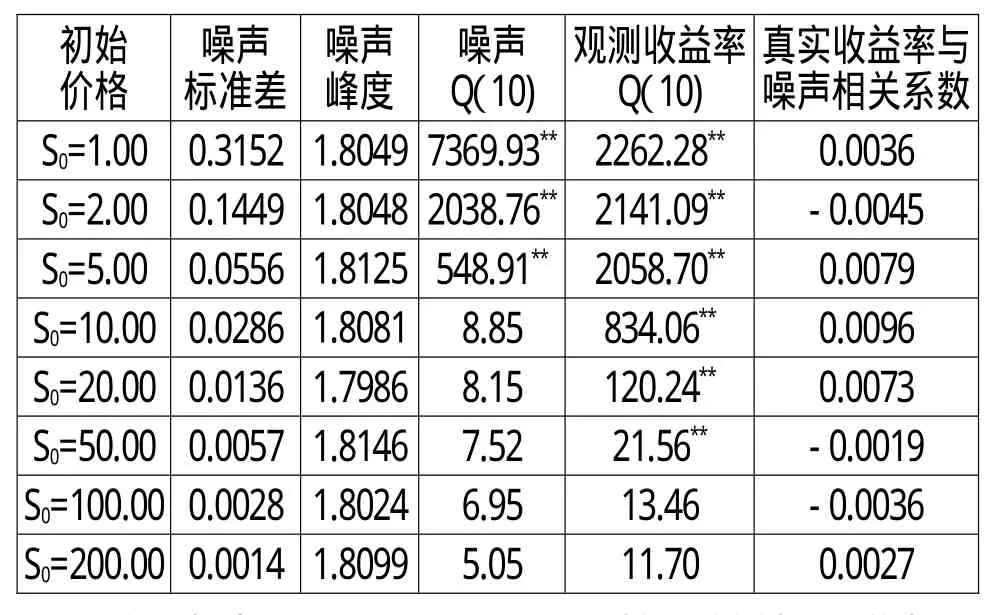
表1 价格离散形成的微观结构噪声的统计特征

表1的结果充分说明了价格离散对低价格资产影响更为严重，其中噪声标准差与初始价格呈反比例关系，噪声和观测收益率的自相关性随着初始价格的减小而增大。在资产价格较小时，噪声序列表现出明显的自相关性，具体表现为自相关函数和偏自相关函数拖尾①由于初始价格的情况比较多，此处不再给出相关图形，而是直接描述相关结果。后文中涉及类似的情况时，除有特别需要外，均采用直接描述的方式。，呈现AMRA模型的结构，而在资产价格较大时，噪声序列表现为白噪声。与此同时，观测收益率的自相关结构由噪声的自相关结构直接决定，即当噪声表现为自相关或者影响较大的白噪声时，观测收益率呈现MA（1）结构，而当噪声为影响较小的白噪声时，观测收益率也呈现为白噪声。另外，真实收益率②这里采用真实收益率而没有采用真实对数价格，是因为考虑到真实收益率与噪声一样都是平稳过程，更容易发现二者之间的相关性。如果将真实收益率替换为真实对数价格过程，也会得到类似的结论。与噪声的相关系数普遍较小，可以认为二者之间不存在显著的相关性。

除此之外，价格离散还是高频数据中“零收益率”现象产生的主要原因。在给定的观测频度下（例如1分钟），当价格的波动幅度小于价格离散阈值时，价格的变化将被“截断”，具体表现为这1分钟之内没有价格变化，进而导致“零收益率”的产生。因此，由价格离散导致的“零收益率”问题不仅与真实波动率的大小有关，还与该高频区间内的真实资产价格的绝对大小有关。价格越低的资产其高频的波动越不容易超过价格离散阈值，因此越容易发生“零收益率”现象。

（三）非频繁交易

非频繁交易（infrequent trading）又称为不频繁交易，顾名思义指的就是存在无交易的情形。在较高的观测频率下，金融资产经常都有无交易的情况发生，特别是对于活跃度较低的资产。在无交易的情况下，资产价格将保持上一个时刻的价格，进而形成“零收益率”的现象。非频繁交易和价格离散都是“零收益率”现象的原因，这两种形式统称为“刚性交易”（flat trading）。与价格离散不同的是，非频繁交易形成零收益率只与活跃度有关，而与资产价格无直接关系。

在考虑流动性度量时，Lesmond et al.(1999)及Holden(2009)都给出了考虑无交易情形的买卖价差估计，改进了Roll(1984)[9]的模型，并提出“零收益率”也是流动性的重要度量方式之一。为了排除买卖价差的因素，单独考虑非频繁交易形成的微观结构噪声，这里采用Piillips和Yu(2008)给出的模型：

其中ξit为表示是否存在交易的随机变量，服从伯努利分布，且E(ξit=1|Ωt)= πt为第t个交易日发生交易的概率，相应地1-πt为无交易概率。此时，由非频繁交易产生的微观结构噪声为

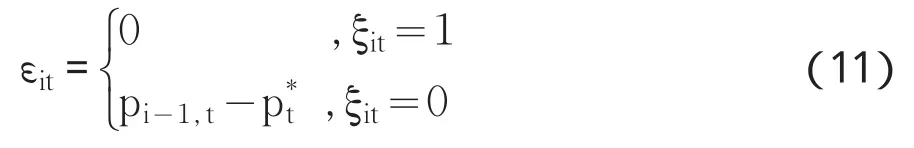
显然，由（11）式定义的微观结构噪声直接取决于πt的大小，即交易概率决定了微观结构噪声的程度。图3给出了噪声及其分布的模拟图形③此处给出的模拟设定是日内4个小时的分钟数据，且S0=10.00，π=0.8。。

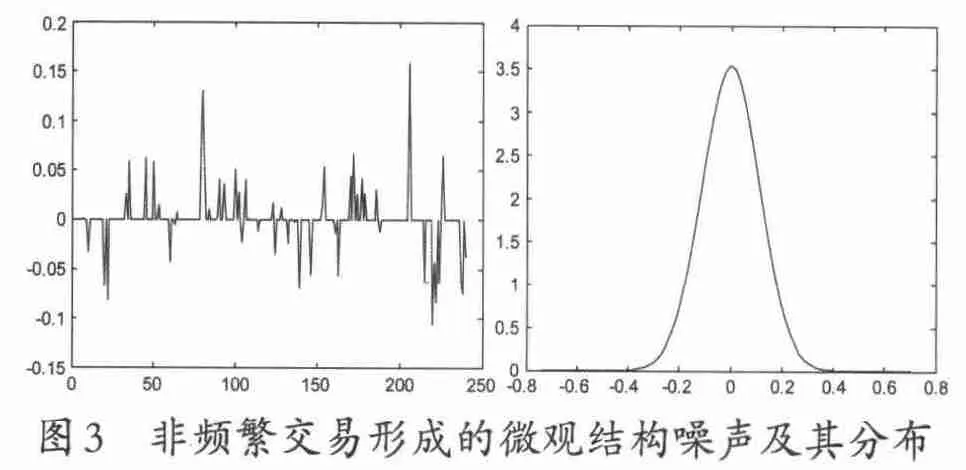
从图3的结果来看，由非频繁交易形成的微观结构噪声与价格离散的情况相反，其分布呈现“尖峰厚尾”的形态。由于不同的交易概率形成的噪声程度不同，这里我们在固定初始价格为10.00元的条件下，将交易概率分为从0.1至0.9分别进行考察。具体模拟结果如表2所示。

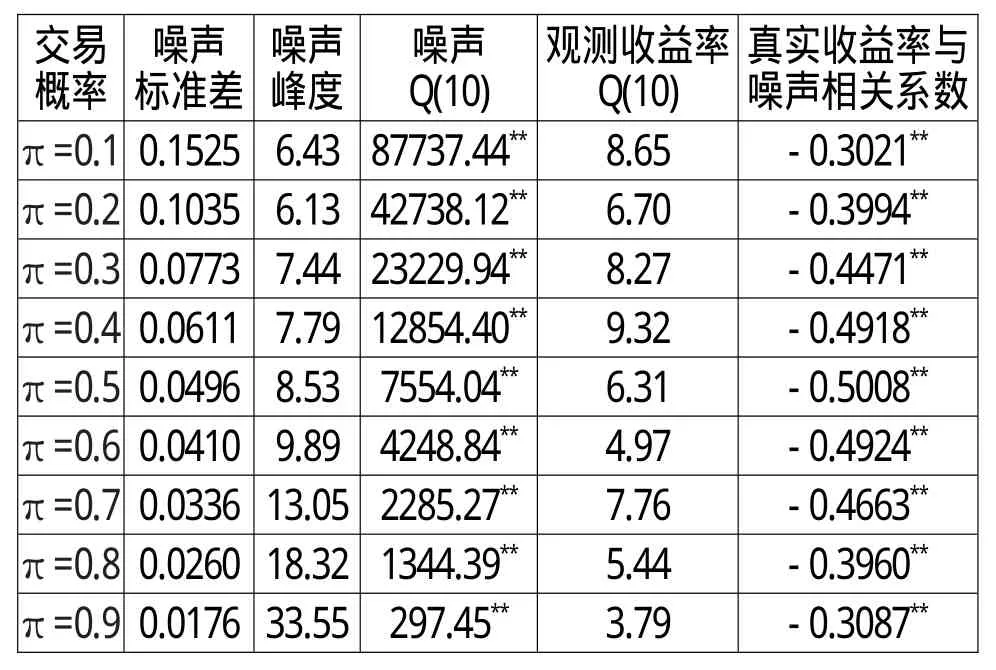
表2 非频繁交易形成的微观结构噪声的统计特征

表2的结果说明非频繁交易的程度越严重（交易概率越低）则由其形成的微观结构噪声标准差越大，同时噪声的峰度随标准差的增大而减小，但仍然表现为明显的“尖峰厚尾”形态。由非频繁交易形成的微观结构噪声具有很强的自相关性，具体表现为自相关函数拖尾、偏自相关函数一阶截尾，是一个典型的AR(1)结构。由于噪声序列表现为明显的正自相关，因此观测收益率表现为类似于白噪声的自相关结构，与（5）式的结果相互印证。另外，真实收益率与噪声表现为显著的负相关，并且这种负相关在交易概率π=0.5时最明显。

通过以上的分析，不难发现由非频繁交易形成的微观结构噪声最具复杂性，其不但有明显的自相关性，而且还与价格过程本身有关。然而，如果直接通过观测数据进行分析，此时的观测收益率又表现为类似于白噪声的结构，因此直接利用价格数据对非频繁交易进行推断是难度较高的。

四、实证分析

本节采用沪深A股股票和股指期货的高频交易数据进行实证分析，共选择了四只股票，分为两个对比组①这里的高价股和低价股是同行业组内的相对概念，即在整个观测期间高价股的价格均大于低价股的价格。：平安银行（高价股）和工商银行（低价股）、贵州茅台（高价股）和皇台酒业（低价股），以及股指期货主力合约作为更高价格的交易资产作为参考。观测样本期间为2010年4月16日至2013年4月15日共726个交易日，样本数据包括1分钟开盘价、最高价、最低价和收盘价，以及成交量和成交金额。

（一）“零收益率”分析

根据上一节的理论，“零收益率”现象是由价格离散和非频繁交易共同导致的。通过成交量的数据，我们可以简单地使用成交频率对交易概率进行估计。表3简单地展示了5个资产在不同观测频率下的成交频率。

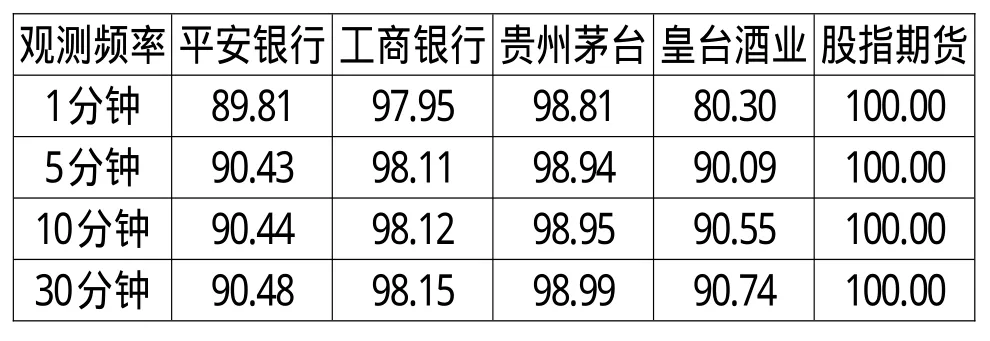
表3 不同资产的成交频率（%）

由于国内A股和股指期货的交易状态一直比较活跃，因此非频繁交易的程度与国外相比要小很多。表3当中交易概率相对较低的有皇台酒业和平安银行，其中平安银行是由于2010年6月30日至2010年9月1日停牌所致，因此并不能归结于高频的非频繁交易。由于皇台酒业活跃度相对较低，即存在非频繁交易的现象，因此对比表2的结果可以推测其噪声可能存在与收益率的相关性。

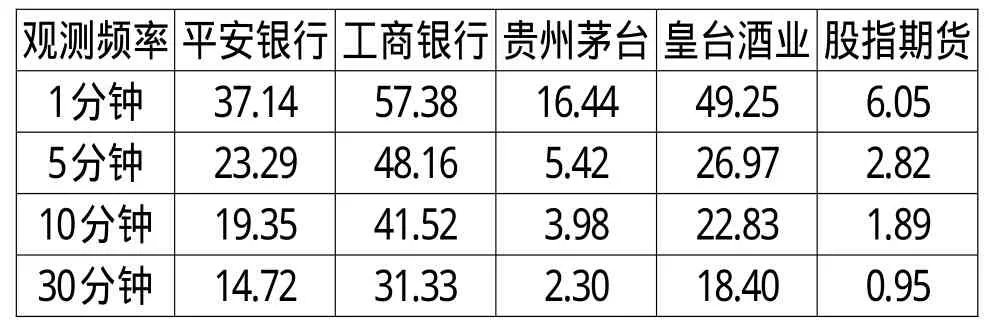
表4 不同资产的零收益率比例（%）

表4显示了零收益率的比例，对比表3的结果可以发现并不是非频繁交易的程度越高零收益率的比例越高，但非频繁交易仍有一定的影响。根据上一节的理论，价格离散也是零收益率的重要形成因素，而且对价格低的资产尤其显著。上述5个资产的平均价格分别为16.69元、4.21元、193.48元、13.26元和2755.64元，可以发现零收益率的比例和这一价格水平基本上成反比关系，特别是股指期货的零收益率明显较少。综合表3和表4的结果可以发现，即使交易活跃度很高的资产“零收益率”现象也非常显著，这说明价格离散是形成零收益率的最主要原因。

（二）噪声的相关性检验

由于真实的价格过程不可观测，所以针对没有序列相关的噪声存在与否的考察，常常可以利用（4）式的结论。但对于存在序列相关的噪声，（5）式和表2都说明了观测收益率的自相关函数难以揭示噪声的表现。为此，我们采用韩清和刘永刚（2007）[8]的基于两尺度调整已实现波动率差的检验方法来对噪声的相关性进行考察。表5给出了具体检验结果。

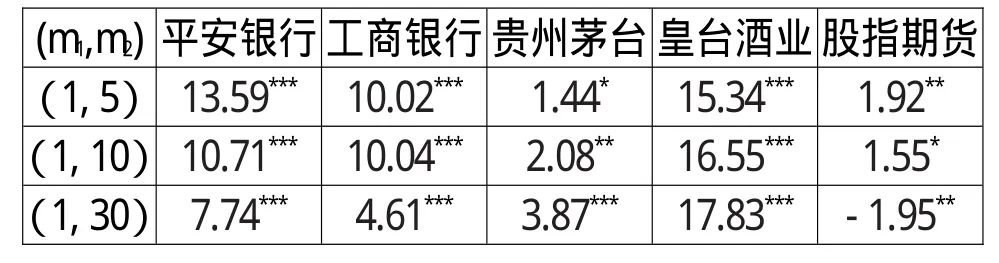
表5 不同资产的噪声相关性检验结果（%）

表5给出了3种时间尺度组合的噪声相关性检验结果。由于1分钟和5分钟的时间间隔太短，30分钟的日内样本量太少，因此（1，10）的组合最具参考价值。从结果上来看，皇台酒业由于非频繁交易最严重，因此噪声与价格可能存在相关，具体表现为统计量显著，与表2的结果相印证。另外，价格高的资产受到价格离散的影响小，因此噪声的自相关程度也较小，特别是股指期货的噪声相关性与其他相比要小很多，这与前面的分析结果相吻合。即便如此，股指期货仍然表现出较显著的噪声相关性，这可能是本文未涉及的非同步交易等机制所形成的。

五、结论

本文将市场微观结构的价格形成机制理论引入到市场微观结构噪声的研究当中，具体考察了噪声的三种形成机制：买卖价差、价格离散和非频繁交易。其中，价格离散和非频繁交易又是“零收益率”现象这种特殊噪声形式的产生原因。根据噪声的形成机制模型，我们利用蒙特卡罗模拟探索了每种机制下噪声的表现形式，得到的结论如下：

（1）买卖价差是最直接的噪声形成原因之一，其产生的噪声形式依赖于对买卖价差的假设。利用传统的买卖价差模型得到的微观结构噪声形式较为简单，基本上满足微观计量中常用的三个假设条件。

（2）价格离散是最主要的噪声形成原因之一，价格越低的资产越容易受到价格离散的影响，并且噪声的分布呈现“低峰薄尾”的形态。价格较低的资产形成的噪声具有一定程度的自相关性，但与真实收益率的相关性不明显。

（3）非频繁交易是最复杂的噪声形成原因之一，由其产生的噪声分布呈现“尖峰厚尾“的形态，并且噪声保持较高的自相关性，而且还与真实收益率之间有显著的负相关关系，总体而言基本上不满足传统的噪声假设条件。

实证分析考察了沪深A股股票市场和股指期货等多个资产。一方面对“零收益率”现象进行了分析，总结出了价格离散比非频繁交易更适合解释我国股票市场的“零收益率”现象；另一方面对噪声的相关性进行了检验，检验结果总体与理论和模拟的结果相吻合，进一步揭示了三种噪声形成机制对我国股票市场的综合影响特征。

市场微观结构噪声的形成机制是其微观计量假设的理论支撑，因此也是正确应用波动性和流动性理论的先决条件。对价格形成机制和噪声产生逻辑的理解，有助于我们对市场微观结构和运作机制的进一步认识，找到适合不同市场分类的微观结构噪声假设条件，最终实现更精确的资产定价和风险管理效果。

[1]Black,F.Noise[J].The Journal of Finance,1986,3:529-543.

[2]Mad havan,A.Market Micro structure:A Survey[J].Jounarl of Financial Markets,2000,3:206-258.

[3]O’Hara,M,Market Microstructure Thery[M].Oxford:Blackwell,1995.

[4]Stoll,H.Market Microstrurcture[M].Hand book of Economics and Finance.Elasever Science B V,2003.

[5]Hasbrouck,J.Empirical Market Microstructure[M].The Institutions,Economics,and Econometrics of Security Trading.Oxford,2007.

[6]Bandi,FM,and JR Russell.Separating Microstructure Noise from Volatility[J].Journal of Financial Economics,2006,79:655-692.

[7]Hansen P R,and A Lunde.Realized Variance and Market Microstructure Noise[J].Journal of Business and Economic Statistics,2006,2:127-160.

[8]韩清，刘永刚.序列相关的微观结构噪声估计[J].数量经济技术经济研究，2007，（4）：92-102.

[9]Roll,R.A Simple Implicit Measure of the Effective Bid-Ask Spread in an Efficient Market[J].The Journal of Finance,1984,4:1127-1139.

[10]Rosenbaum,M.Integrated Volatility and Round-Off Error[J].Bernoulli,2009.

1003-4625（2014）07-0007-06

F832.5

A

2014-04-08

刘威仪（1987-），男，四川乐山人，博士研究生，研究方向：金融计量，金融市场及其微观结构。

王淑云）