基于alpha稳定分布的盲信号分离

任 静，李维勤，惠 鏸

REN Jing1,LI Weiqin2,HUI Hui2

1.西安航空学院 计算机工程系，西安 710077

2.西安理工大学 自动化与信息工程学院，西安 710048

1.Department of Computer Engineering,Xi’an Aeronautical University,Xi’an 710077,China

2.School of Automation and Information Engineering,Xi’an University of Technology,Xi’an 710048,China

1 引言

盲信号分离是目前信号处理领域的研究热点问题，获得了迅速发展和广泛应用[1-5]。盲信号分离是指在未知源信号和传输通道参数的情况下，依据某种准则，仅仅由观测信号恢复出源信号，其算法的性能依赖于信号的概率分布特性。信号的峭度（峰度）对信号概率分布特性的影响较大。一个信号y的归一化峭度定义为：

当归一化峭度为负值时，则称该信号为轻拖尾信号，也称亚高斯信号；当峭度为正值时，则该信号为重拖尾信号，也称超高斯信号。重拖尾信号的概率密度函数的拖尾较重。

传统的盲分离算法对于轻拖尾和重拖尾信号混合时的分离效果一般。为此，相关学者提出一些改进算法，其核心是自适应动态切换，对重拖尾信号和轻拖尾信号分别取不同的非线性函数。但是由于评价函数采用固定非线性函数，因而分离准确度一般。近年来，针对此问题逐渐发展了一些参数化和无参化学习算法[6-9]，这类算法采用准确的概率分布估计方法，准确估计信号的概率密度函数和评价函数，从而提高了算法的分离性能，但是计算复杂度较高，并要求源信号为平稳信号。

然而，当源信号为重拖尾信号时，特别是冲击特性较强的非平稳信号，其二阶及以上各阶矩趋于无穷大，传统的盲信号分离算法效果一般。针对此问题，相关人员开展了相关研究工作，取得了一定进展[10-14]。但是，这些算法的计算复杂度较高，分离效果一般，难以满足在线学习算法的需要。

本文基于alpha稳定分布的概率分布估计方法，采用数值计算方法和人工神经网络方法估计信号的概率密度函数和评价函数，提出基于alpha稳定分布的盲信号分离算法，最后对算法进行仿真实验分析。

2 盲信号分离算法原理

假设S(t)为源信号，其维数为m，A为m×n阶混合矩阵，X(t)=AS(t)为实际观测得到的m维数据向量。盲信号分离问题就是在A和S(t)均未知的情况下，在仅知道观测数据X(t)的条件下，依照某种分离准则，找出分离矩阵W，使得恢复信号Y(t)=WX(t)尽可能接近源信号S(t)。由于对源信号和混合矩阵未知，因此对于盲信号分离问题必须知道分离准则，一般假定源信号之间统计独立。

基于最小互信息的自然梯度学习算法目前得到了广泛应用[3]。一个多维随机信号Y的独立性可以由其互信息表示，即联合概率密度函数 p(Y;W)和边缘概率密度函数乘积之间的Kullback-Leibler距离：

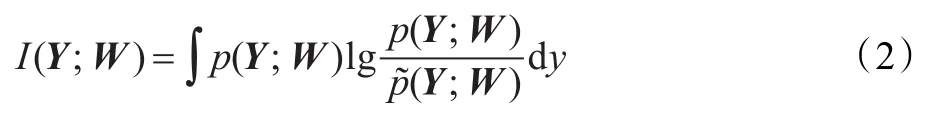
当信号Y的各维变量 yi之间的互信息越小时，其各维分量之间相互统计独立。其代价函数为：

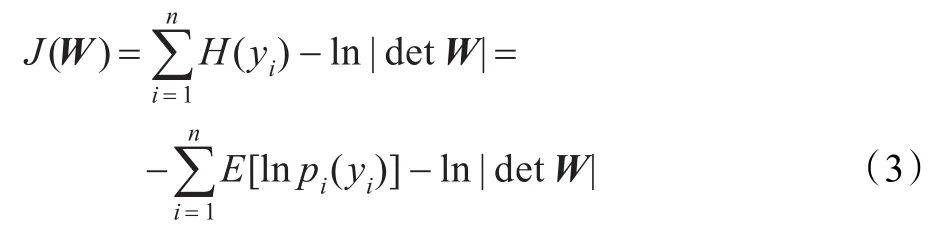
式中，H(yi)表示信息熵。

采用自然梯度算法，可得到[3]：

式中，I表示单位矩阵，η代表学习率，ϕ(y)是评价函数，如下式所示：

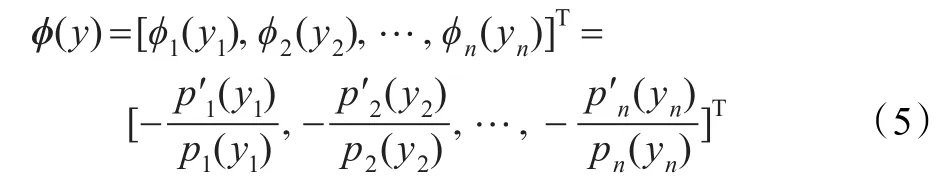
式中，p(yi)和 p′(yi)分别表示概率密度函数及其一阶导数。

近年来提出的一些盲信号分离算法，包括Kernel ICA、非参数ICA算法，通过准确估计信号的概率密度函数，可以实现源信号的准确分离[6-9]。但是这类算法计算复杂度较大，并假定源信号为平稳信号，当源信号包含非平稳信号时，算法可能不收敛。而alpha稳定分布可以准确描述信号的概率分布特性。

3 基于alpha稳定分布的评价函数估计

3.1 概率密度函数估计

Alpha稳定分布是一种连续概率分布类型，它是一类允许重拖尾和偏度的概率分布的总和。Alpha稳定分布形态取决于其四个参数，即特征参数、对称参数、尺度参数和位置参数。特征参数控制密度函数拖尾的厚度和长度，其值越小拖尾越长。对称参数决定稳定分布的斜度，其值越大信号的概率密度函数越不对称。尺度参数决定概率密度函数的聚集程度，其值越大信号的分布越集中。位置参数决定信号的中心点位置。

虽然alpha稳定分布具有广义特性，但是无法用具体的函数形式表示其概率密度函数。一般情况下，alpha稳定分布用其特征方程来描述，如下式所示[15-16]：

一个信号Y的概率密度函数是其特征函数的傅里叶变换，即

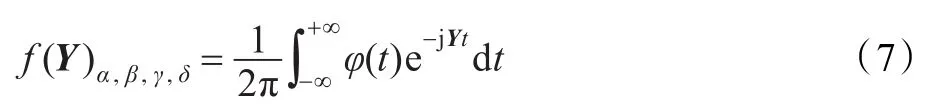
对于一个服从标准alpha稳定分布的随机变量Y（γ=1且 δ=0），公式（7）可简化为：

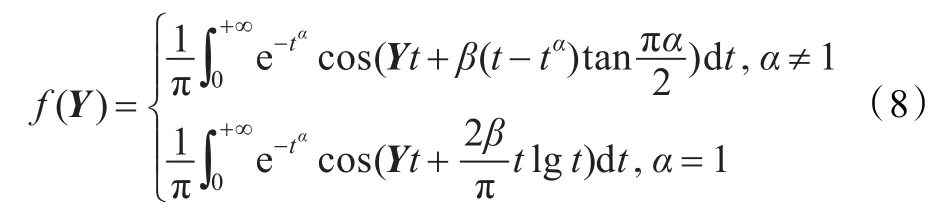
对于盲信号分离问题来说，由于每次迭代过程需要对数据进行中心化处理，位置参数δ为零。这种情况下一个服从非标准alpha稳定分布的信号X的概率密度函数可通过如下变换来生成：

其中，X=Y/γ。

对于一个经过中心化处理的信号Y，首先估计其三个参数值 α，β，γ[17]，然后对式（8）用快速傅里叶变换（FFT）算法求解，并通过式（9）变换得到一个样本点所对应的概率密度函数值[18-19]。FFT算法具有较好的计算精度和较快的计算速度，然而，FFT难以满足实际在线盲信号分离算法的需要，特别是对于大样本信号，其计算复杂度较高。

为此，本文提出如下的离线和在线结合的两步概率密度函数估计方法。即采用FFT算法离线计算标准alpha稳定分布的概率密度函数库查找表，然后在线估计信号的三个参数并进行查找。具体过程如下：首先，对具有不同特征参数和对称参数值的标准alpha稳定分布，离线建立概率密度函数库查找表，即对特征参数α和对称参数β分别在其可取的区间，均匀选取有限个样本。例如，对于 α ，可取 α0，α1，…，αi，…，αn，αi=2i/n 。在每一个离散点(αi，βj)，计算其概率密度函数值，建立查找表。接下来，对于待估计信号X，在线估计信号的特征参数、对称参数和尺度参数，然后查找(αi，βj)所对应的概率密度函数值，最后根据式（9）进行变换就可得到概率密度函数值。

3.2 评价函数估计

估计信号的评价函数需要估计概率密度函数导数，传统的数值微分方法并不准确。由于神经网络具有很好的非线性逼近能力，因此本文采用一个单隐层神经网络来估计概率密度函数的导数。

让 yi，i=1，2，…，m 是神经网络的输入，p(yi)，i=1，2，…，m是神经网络的输出，m表示样本的个数，隐层神经元的激活函数为tanh，如图1所示，当神经网络训练完成时，网络的传递函数满足H(y，W)=p(y)，即

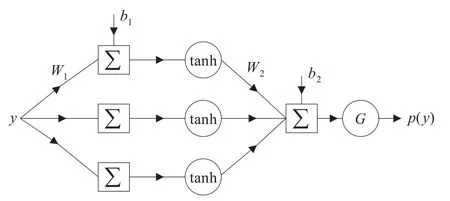
图1 神经网络结构图

因此，概率密度函数的导数 p′(y)为：

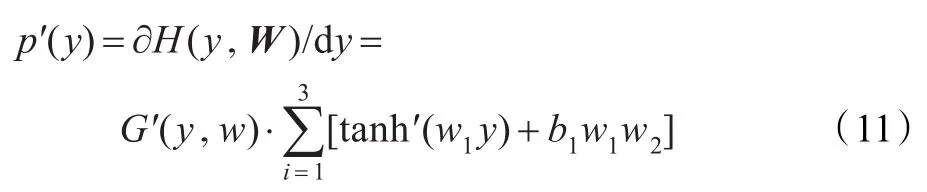
上述神经网络求解概率密度函数导数的过程如下：首先设置神经网络的初始权值，令 p(y)为神经网络目标输出；接下来迭代调整神经网络的权重w(t+1)=w(t)+η(t)∂ε(w)/∂w，ε(w)表示目标函数；重复执行上述过程，直到收敛为止；最后当神经网络训练完成时，通过求解式（11）可得到信号 y的概率密度函数的导数。一旦得到了概率密度函数的导数，则可以通过式（5）获得信号的评价函数ϕ(y)。

综上所述，本文算法的简化过程如下：

（1）对特征参数和对称参数在其可取的区间内，均匀选取有限个离散点；对每一个离散点，采用FFT算法离线计算标准重拖尾信号的概率密度函数，建立查找表。

（2）在线估计混合信号每一维数据 yi的特征参数、对称参数和尺度参数。

（3）在查找表中查找参数值所对应的概率密度函数f(yi)；根据式（9）求得概率密度函数值。

（4）根据式（11）和式（5）计算信号的评价函数。

（5）根据式（4）迭代求解分离矩阵W 。

4 仿真实验

信号源如图2所示，图中从上到下依次是一个冲击信号、高斯白噪声、正弦波信号、锯齿波信号，其归一化峭度分别为14 465，0，-0.377 8，-0.127 8。这属于重拖尾信号和轻拖尾信号混合情况，其中第一个源信号具有典型的重拖尾分布特性，冲击特性较强。混合矩阵A为4×4的随机矩阵，即观测信号维数等于源信号维数。然而，实际情况信源维数是未知的。如果观测信号维数大于源信号维数时，属于超定问题，常见的方法是先估计信号的维数，然后再进行信号的分离[20-22]。如果观测信号维数小于源信号维数时，则属于欠定问题[23-25]。本文仅考虑观测信号维数等于源信号维数情况。

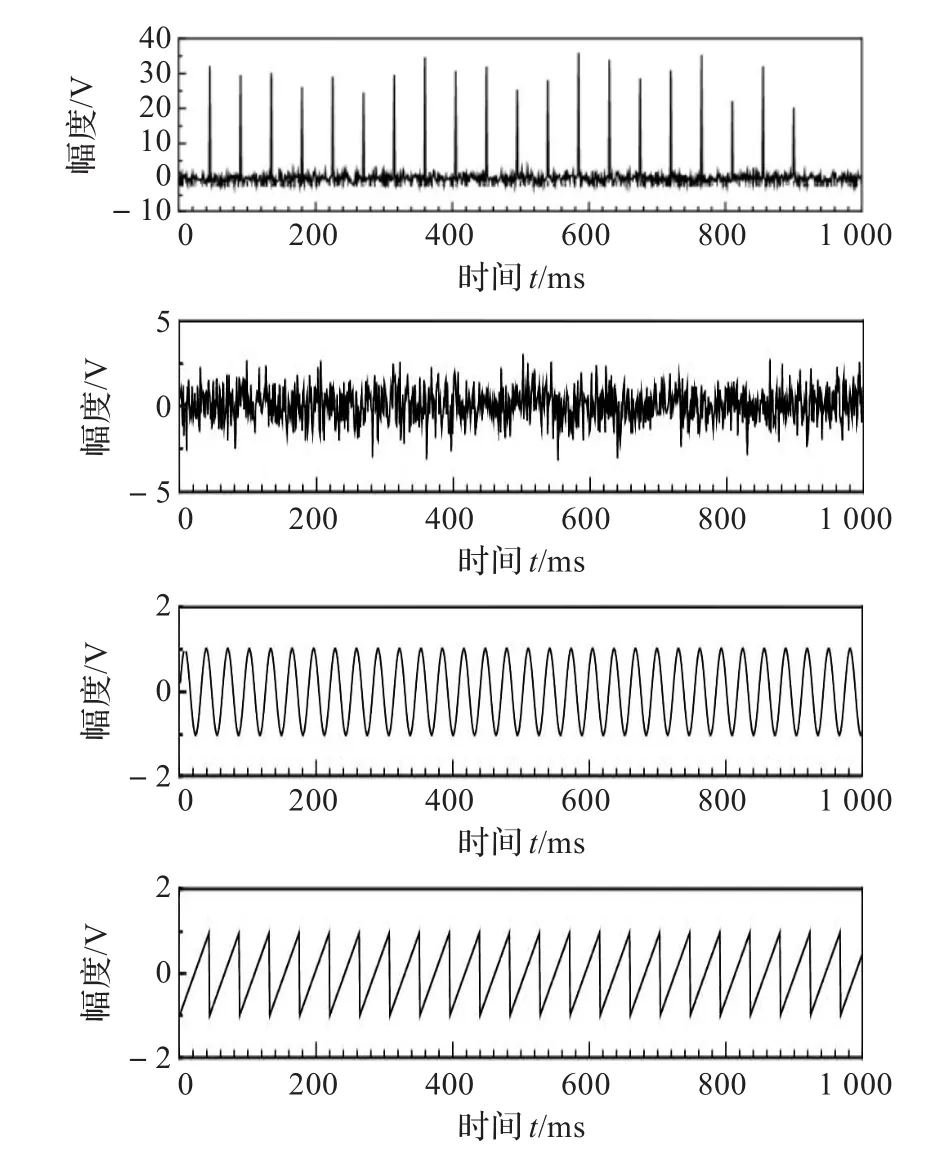
图2 源信号

分别选取扩展最大熵算法[4]、Kernel ICA算法[9]、非参数ICA算法[6]以及本文提出的算法，分析算法的分离效果。图3是混合信号，混合矩阵A为随机矩阵。从图中可以看出，混合后的信号均呈现高斯白噪声和冲击信号的特征。

图3 混合信号

图4是采用本文算法估计的结果。从图中可以看出，本文算法可以恢复出源信号。需要指出的是，恢复信号的顺序与源信号不一致，这是盲信号分离的固有特性[5]。

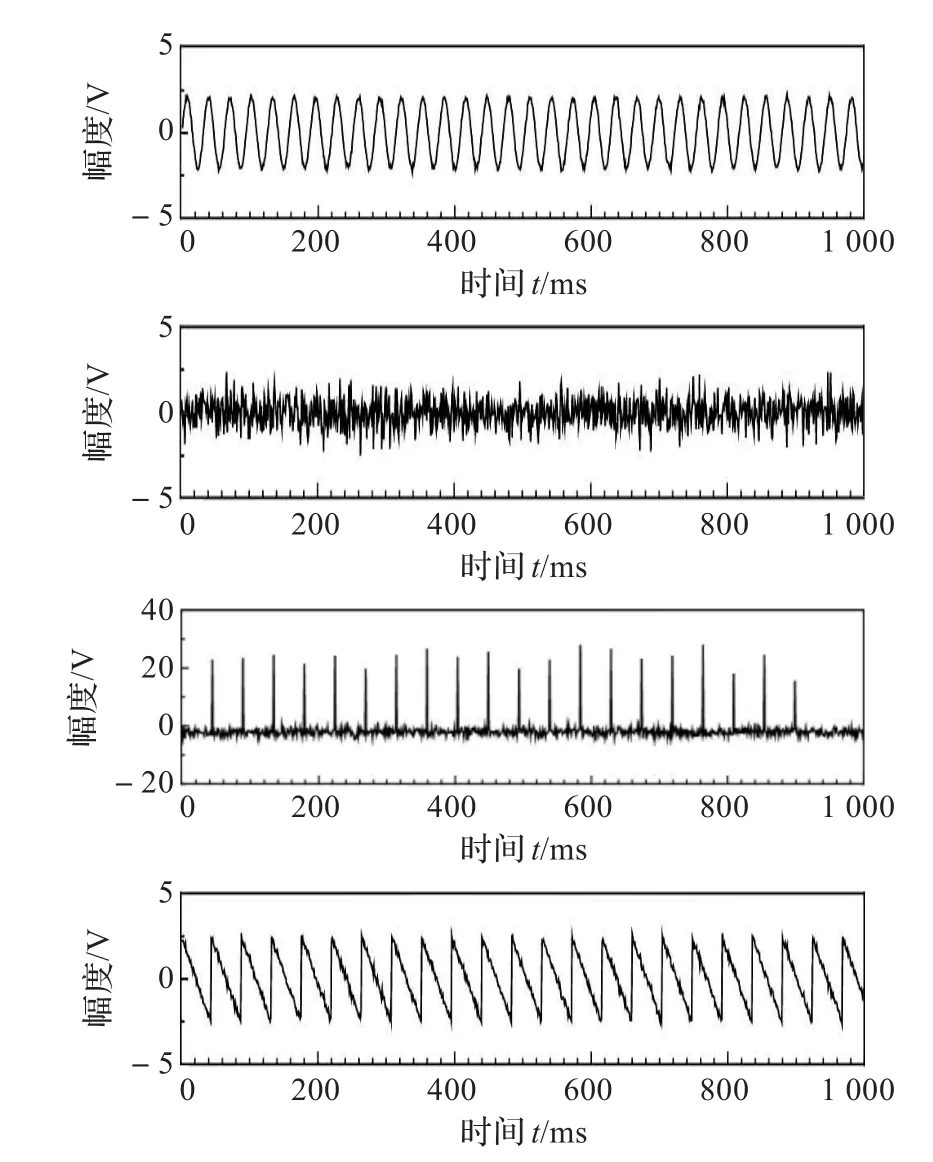
图4 恢复信号

图5是非参数化ICA算法的分离结果。从图中可以看出，该算法也可以恢复源信号。但是，算法的恢复效果一般，特别是锯齿波分离信号受冲击信号的干扰并未完全消除。

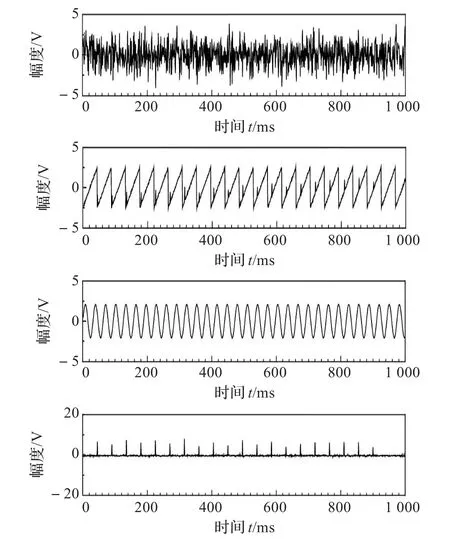
图5 基于非参数ICA的分离结果

为比较各分离算法的分离性能，定义源信号S与源信号和恢复信号Y之差的比值作为恢复信号的信噪比（SNR），作为衡量分离效果的指标[5]，即

式中，M表示信号样本维数。显然，恢复信号与源信号越接近，L值越大，信号恢复效果越好。

图6给出了几种算法的分离效果。从图中可看出，不管是小样本和大样本数据，本文提出算法的分离效果优于其他算法。

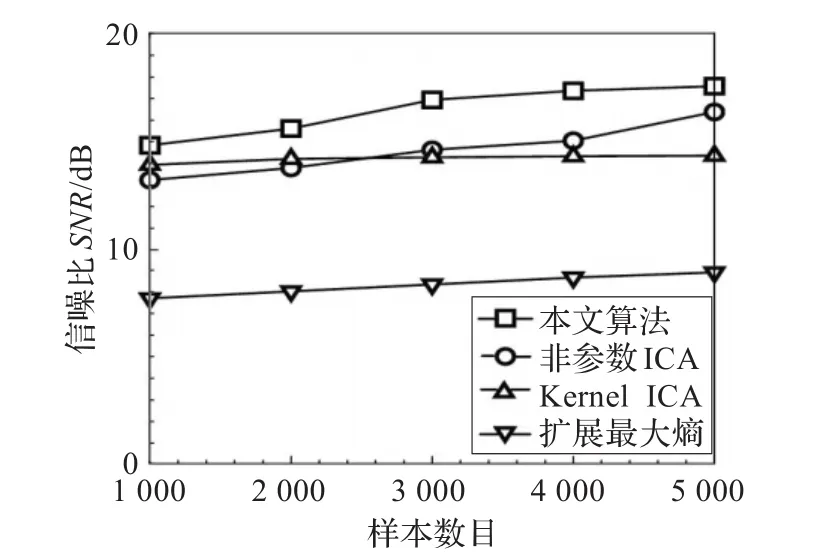
图6 不同算法的分离效果

接下来分析算法的计算复杂度。以非参数ICA算法和本文提出的算法作比较。图7给出了取不同样本个数时两种算法所消耗的计算时间，源信号的维数为6。从图中可看出，当样本数目较小时，本文算法与非参数ICA算法计算时间基本相等；当样本数目较大时，本文算法的计算时间明显小于非参数ICA算法。实际上，非参数ICA算法一般需要用到大部分样本，其计算复杂度近似为O(M2N2+M2N)，M和N分别表示样本维数和个数[6]。而本文算法的计算复杂度包含两个方面，一方面参数估计算法的计算复杂度约为O(BMN2C)，其中，B为迭代次数，NC表示选取的样本个数；其次是评价函数估计，其计算复杂度约为O(MN)。总的计算复杂度近似为O(AMN2C+MN)。当样本个数较大时，NC远小于N，本文算法计算复杂度较低。

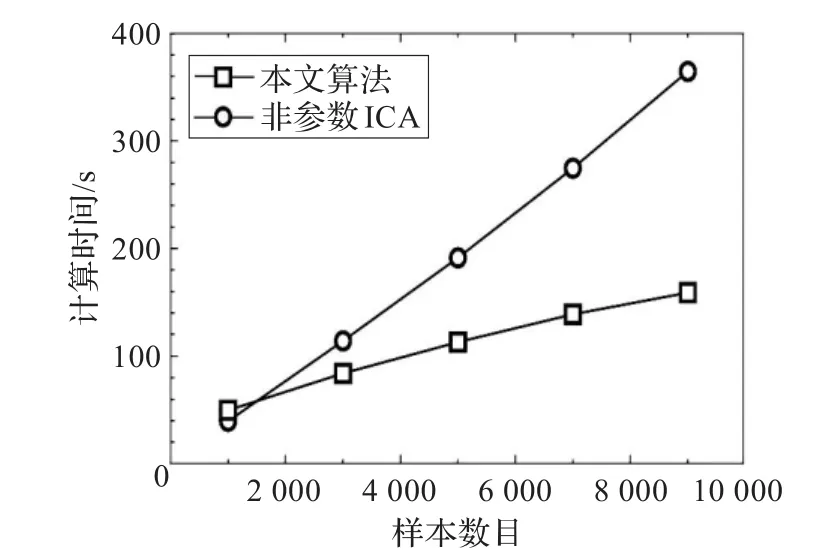
图7 不同算法的计算时间

下面分析不同拖尾特性混合信号的算法分离性能。表1给出了源信号维数为2时的不同拖尾特性混合信号分离结果的信噪比，样本数目为5 000，表中前两行、第三行、最后两行分别是重拖尾混合信号、重拖尾轻拖尾混合信号、拖尾特性非常弱的混合信号的分离结果。可以看出，对于不同拖尾特性混合信号，本文算法均具有较好的分离性能。

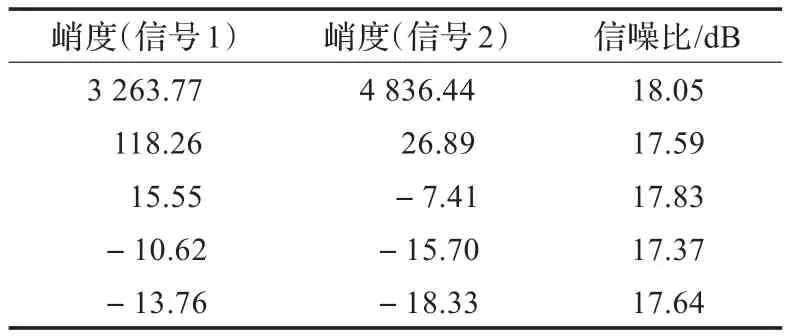
表1 不同拖尾特性混合信号分离结果的信噪比

5 结束语

本文提出了一种基于alpha稳定分布的盲信号分离算法。首先采用FFT方法估计信号的概率密度函数，建立标准alpha稳定分布概率密度函数库查找表。然后在线估计混合信号的特征参数、对称参数和尺度参数，从而获得其概率密度函数。最后采用多层神经网络准确估计信号的评价函数。本文算法不需要源信号的先验知识，适用于具有任意概率分布特性信号的盲分离。仿真结果表明，本文算法具有较高的分离性能和较低的时间复杂度。

[1]Common P.Independent component analysis，a new concept?[J].Signal Processing，1994，36：287-314.

[2]Pham D T，Cardoso J F.Blind separation of instantaneous mixtures of nonstationary sources[J].IEEE Transactions on Signal Processing，2001，49（9）：1837-1848.

[3]Yong H H，Amari S.Adaptive on-line learning algorithm for blind separation：maximum entropy and minimum mutual information[J].Neural Computation，1997，7：1457-1482.

[4]Lee T W，Girolami M，Sejnowski T J.Independent component analysis using an extended infomax algorithm for mixed sub-Gaussian and super-Gaussian sources[J].Neural Computation，1999，11（2）：417-441.

[5]张贤达，保铮.盲信号分离[J].电子学报，2001，29（12A）：1766-1770.

[6]Boscolo R，Pan H，Vwani P R.Independent component analysis based on nonparametric density estimation[J].IEEE Transactions on Neural Networks，2004，15（1）：154-161.

[7]Novey M，Adal T.Complex ICA by negentropy maximization[J].IEEE Transactions on Neural Networks，2008，19（4）：596-609.

[8]Li W Q，Zhang H B，Zhao F.Independent component analysis using multilayer networks[J].IEEE Signal Processing Letters，2007，14（11）：856-858.

[9]Bach F R，Jordan M I.Kernel independent component analysis[J].Journal of Machine Learning Research，2002，3：1-48.

[10]Zarzoso V，Common P.Robust independent component analysis by iterative maximization of the kurtosis contrast with algebraic optimal step size[J].IEEE Transactions on Neural Networks，2010，21（2）：248-261.

[11]Yeredor A.Blind separation of Gaussian sources with general covariance structures：bounds and optimal estimation[J].IEEE Transactions on Signal Processing，2010，58（10）：5057-5068.

[12]Zarzoso V，Comon P，Phlypo R.A contrast function for independent component analysis without permutation ambiguity[J].IEEE Transactions on Neural Networks，2010，21（5）：863-868.

[13]Lahat D，Cardoso J F，Messer H.Second-order multidimensional ICA：performance analysis[J].IEEE Trans on Signal Processing，2012，60（9）：4598-4600.

[14]王莹，李宏伟，付红伟.HT-LSM的欠定混合盲信号分离方法的研究[J].计算机工程与应用，2010，46（32）：133-136.

[15]Nolan J P.Numerical calculation of stable densities and distribution functions[J].Communication Statist-Stochastic Models，1997，13：759-774.

[16]Wang B J，Ercan E K，Zhang J Y.ICA by maximizing non-stability[C]//8th International Conference on ICA and Signal Separation，Paraty，Brazil，2009，5441：179-186.

[17]郝燕玲，单志明，沈锋.基于DRAM算法的α稳定分布参数估计[J].华中科技大学学报，2011，39（10）：73-78.

[18]Diego S G，Kuruoglu E E，Ruiz D P.A heavy-tailed empirical Bayes method for replicated microarray data[J].Computational Statistics and Data Analysis，2009，53（5）：1533-1546.

[19]Kuruoglu E E.Density parameter estimation of skewed α-stable distributions[J].IEEE Transactions on Signal Processing，2001，49（10）：2192-2201.

[20]Cao J，Murata N，Amari S，et al.A robust approach to Independent Component Analysis of signals with high level noise measurements[J].IEEE Transactions on Neural Networks，2003，14（3）：631-645.

[21]李维勤.基于混合信号概率密度函数估计的盲信号分离[D].西安：西安电子科技大学，2005.

[22]冶继民，张贤达，金海红.超定盲信号分离的半参数统计方法[J].电波科学学报，2006，21（3）：331-336.

[23]冶继民，张贤达，朱孝龙.信源数目未知和动态变化时的盲信号分离[J].中国科学：E辑，2005，35（12）：1277-1287.

[24]肖明，谢胜利，傅予力.基于超平面法矢量的欠定盲信号分离算法[J].自动化学报，2008，34（2）：142-149.

[25]冯涛.欠定盲源分离算法研究[D].成都：电子科技大学，2012.