边际结构模型基本原理及其应用实例介绍*

田丹平 张 敏 黄渊秀 高 林 董 晶 李 黎 邓 欣 杨 芳 胡国清

由于观察性研究无法随机分配不同处理组的暴露水平，故在暴露变量和结局变量间的因果关联推断方面无法获得与随机对照试验同等质量的证据。针对观察性研究的这一不足，国外学者在过去的几十年中先后提出了一些新的方法。边际结构模型(marginal structural models,MSMs)是近二十年中出现的一类新的因果推断方法，它由哈佛大学的Robins于1999年提出。边际结构模型主要适用于存在时间依赖协变量与时间依赖暴露变量的观察性研究。鉴于目前国内绝大多数医学工作者对边际结构模型尚不熟悉，本文拟简要介绍其基本原理，并结合实例说明其应用。

1.基本概念

(1)时间依赖混杂因素(time-dependent confounders)：变量取值随时间变化而变化的混杂因素。它既影响结局变量，也影响后期的暴露变量。

(2)反事实变量或潜结局变量(counterfactual or potential outcomes)：反事实变量是理论上可能出现但现实却未被观测到的变量。假设欲估计某暴露变量A与结局变量Y的因果关联，A所有可能的取值有J+1种，用a=(0,1,…,J)表示。现实中，任一观察对象某时刻的暴露变量A只能取J+1中的一种。但可以想象，假定第i个观察对象某时刻的暴露值a为j(j=0,…,J)，将有一个与之相对应的结局变量，表示为Yi,a=j。变量Yi,a=j是一个虚拟变量，因为在现实中，观察对象i的暴露变量A只会取0,1,…,J中的一个值，此时，现实中观测不到暴露变量a分别取剩余J-1个值时结果变量Yi,a=j的取值。所有这些暴露值的结局变量Yi,a=j都被称作反事实变量，研究对象i的反事实变量可以用向量(Yi,a=0,Yi,a=1,…,Yi,a=j)表示。通常，我们可以合理假定，当对象i接受暴露Xi=j，实际的结局事件Yi就等于Yi,a=j。对于每一个观察对象，现实中都只能观察到其反事实结局变量向量中一个元素，而向量中其他值在现实中则无法观察到[2,3]。

在时点研究中，令a0=1和a0=0分别表示研究对象接受治疗和未接受治疗，用Ya0=1和Ya0=0分别表示研究对象接受治疗和未接受治疗的结局，即反事实变量。在临床治疗中，无法同时观察到同一研究对象既接受治疗又不接受治疗的结局。如果某研究对象接受了治疗，则此研究对象能观察到的结局Y就为Ya0=1，而无法同时观察到反事实变量向量中的另一取值Ya0=0[1]。

当暴露变量为时间依赖变量时，也可以定义相对应的反事实变量：将时间依赖暴露变量表示为At，t=0,1,…,K，并且在时间点t时At的取值at为0,1,…,J中的一个。对应于任何一个可能的暴露历史，at，t=0,1,…,K，有一个相应的反事实变量，表示为Ya0,a1,…,ak。同样，现实中，因为一个研究对象只有一种暴露历史，因此无法观察到其相应于其他可能的暴露历史的反事实变量。如果t=1，对于试验对象i，当Ai,0=1,Ai,1=0时，那么从时刻0至时刻1期间观察到的结局变量为Yi,a0=1,a1=0，而反事实变量向量的其余部分，如Yi,a0=1,a1=1、Yi,a0=0,a1=1、Yi,a0=0,a1=0则观察不到。下文主要基于时点研究，即t=0时阐述边际结构模型的基本原理及其应用。

2.观察性研究的因果推断图

为帮助理解边际结构模型的基本原理，先简要介绍观察性研究中的因果关联推断图。令：A表示暴露变量，L表示已观测协变量，U表示未观测协变量，Y表示结局变量。图1展示了基线期上述各变量间的3种不同关系。

与图1a相比，图1b中基线期0中缺少由U指向A的箭头，说明A不受U的影响，但受L的影响。在图1c中，既缺少由U指向A的箭头，也缺少由L指向A的箭头，说明A不受混杂因素(即U和L)的影响。仅在图1c的情况下，混杂因素才不影响A与Y之间的因果关联推断，但此类情况在现实中，除非是随机试验，否则基本不存在。

事实上，在观察性研究中，由于无法得到未观测协变量U的数据，当存在U0的影响时(图1a)，如果没有合理的前提假设，任何方法都不能得到A0与Y之间因果关联的无偏估计。故下文介绍的边际结构模型仅针对于只存在已观测协变量L影响的情况(图1b)。

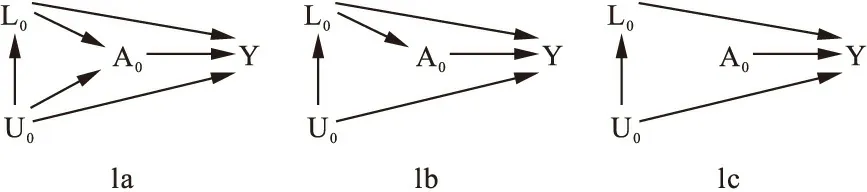
图1 观察性研究中因果关联推断简单示意图(下标0表示基线期，此图即时点研究的因果关联示意图。资料来源：文献[1])

3.边际结构模型的基本数学模型

在时点研究中，可采用线性模型、对数线性模型和logistic回归模型估计暴露变量与结局变量间的因果关联强度，并可获得各研究对象的两个反事实变量P[Ya0=1=1]和P[Ya0=0=1]的估计值，具体模型为：

P[Ya0=1]=ψ0+ψ1a0

(1)

log(P[Ya0=1])=θ0+θ1a0

(2)

logit(P[Ya0=1])=β0+β1a0

(3)

在上述模型中，若研究对象接受治疗(a0=1)时，Ya0=Ya0=1；反之，若研究对象未接受治疗(a0=0)时，Ya0=Ya0=0。模型(1)、(2)和(3)中因果关联强度指标分别为：率差RD=ψ1、相对危险度RR=eθ1、优势比OR=eβ1。

上述模型之所以被称为边际结构模型是因为：模型(1)、(2)和(3)均是建立在Ya0 = 1与Ya0=0的边际分布基础之上，而非二者的联合分布基础之上，故将此类模型称为边际模型。在经济学和社会科学研究领域中常将基于反事实变量的概率模型称为结构模型，故将此类模型称为边际结构模型。

在模型(1)、(2)和(3)中，每个模型都包含两个未知参数且只有两个未知概率P[Ya0=1=1]和P[Ya0=0=1]，因此是饱和模型。

对于存在已观测协变量L影响的情况，可类似构建饱和模型(4)、(5)和(6)获得未调整混杂因素的因果关联强度：

(4)

(5)

(6)

通常，模型(1)、(2)和(3)的参数估计值与模型(4)、(5)和(6)的估计值不相同。仅在暴露变量不受混杂因素影响的情况下，模型(4)、(5)和(6)中的粗估计值才等价于真实的因果关联估计值。

4.边际结构模型的基本原理

在观察性研究中，暴露变量可能受已观测协变量(混杂因素)的影响。边际结构模型正是通过构造已观测协变量与暴露变量的模型，提出校正已观测混杂偏倚的暴露变量逆概率权重，消除已观测协变量的影响，从而获得暴露变量与结局变量间真实的因果关联。

下文以时点研究为例，重点介绍边际结构模型逆概率权重的计算原理。

(1)时点研究中逆概率权重的估算

在时点研究中，研究对象i暴露的逆概率权重的计算公式为：

wi=1/P[A0=a0i|L0=l0i]

其中：loi表示研究对象i的已观测协变量L0的观测值；a0i为研究对象i的暴露变量A0的观测值；P[A0=a0i|L0=l0i]表示研究对象i在L0=l0i的情况下，出现A0=a0i的概率。

可通过拟合A0与L0的logistic回归模型获得观察对象接受暴露的概率P[A0=1|L0=l0]。估计研究对象接受暴露概率的模型为：

logit(P[A0=1|L0=l0])=α0+α1l0

(7)

可通过常用统计软件得到logistic回归模型中参数α0和α1的估计值。若某研究对象实际接受的暴露水平为A0=0，则其接受自身暴露水平的概率为1-P[A0=1|L0=l0]，进而得到各研究对象的逆概率权重wi。

(2)暴露逆概率权重的意义

在无未观测混杂因素影响的假定下，可通过对各研究对象赋予逆概率权重w，来消除已观测协变量L0的混杂影响。例如：对于某研究对象i，若其逆概率权重wi=4，则表示在虚拟人群中该研究对象将会被重复4次。

采用暴露逆概率权重，可在实际观测人群的基础上构造一个虚拟人群，此虚拟人群具有两个重要性质：第一、与在实际人群中不同，在虚拟人群中A0不受L0的影响；第二、在虚拟人群中，P(Ya0=1=1)和P(Ya0=0=1)的概率与在实际人群中相同。因此，可通过逆概率权重控制L0造成的混杂偏倚，得到因果关联的无偏估计。这正是边际结构模型的精髓之所在。

5.边际结构模型与倾向评分法的异同

倾向评分法(propensity score method)由Rosebaum和Rubin于1983年首次提出，是指在一定协变量条件下，一个观察对象可能接受某种暴露的可能性。在非随机研究中，处理组与对照组某些背景特征分布不同，每个个体是否接受“暴露”的概率受其他因素的影响[4]。在倾向评分法中，当一组观测协变量L影响研究对象接受某感兴趣的暴露时(A=1)，在该组协变量的影响下研究对象接受感兴趣的暴露的概率为P(A=1|L=li)，此概率即为研究对象i的倾向评分pi。

倾向评分是反映所观测协变量在两组间均衡性的一个近似函数，它最大限度地概括了协变量的作用。若分别来自暴露组和对照组的两个研究对象具有相同的倾向评分，可认为他们是被随机分配到的两组，接受暴露或者对照的概率相同[4-6]。倾向评分法的假定条件为：计算倾向评分的协变量包括所有影响分组的混杂因素，即不存在未观测的混杂因素[4-5]。

边际结构模型与倾向评分法均是控制混杂偏倚的有力工具，其应用都建立在不存在未观测混杂因素影响的基础之上[1,4]。

与边际结构模型相比，尽管对于接受感兴趣的暴露(A=1)的研究对象而言，1/pi就是边际结构模型中的暴露逆概率权重；但对于未接受感兴趣的暴露(A=0)的研究对象而言，其逆概率权重却不是1/pi，而是1/(1-pi)[1,4]。Robins等人认为，倾向评分法可能受到匹配不充分或层内混杂控制欠佳的影响，特别是在样本量较小时，在控制观测混杂偏倚方面不如边际结构模型[1,6]。

6.应用示例

美国密歇根大学心血管联盟开展的一个多中心合作的观察研究，其主要目的是研究因ST段抬高心肌梗死的住院患者在接受皮冠状动脉介入治疗前使用β受体阻滞剂对治疗结局的影响。其中，术前使用β受体阻滞剂为暴露变量，术中死亡率为结果变量，吸烟状态、高血压、心脏衰竭等因素为协变量，变量赋值见表1。

考虑到本研究为观察研究，且数据初步分析显示协变量明显影响到了暴露变量的取值，故考虑选用边际结构模型来控制协变量的影响。

本例采用边际结构模型，具体步骤如下：

(1)估算研究对象术前使用β受体阻滞剂的概率。参考公式(7)，采用logistics 回归模型拟合边际结构模型，以表1所列的协变量作为自变量，以术前使用β受体阻滞剂与否为因变量，模型估计参数见表2。依据此logistic回归模型估计各研究对象术前使用β受体阻滞剂的概率。

(2)求逆概率权重。按公式wi=1/P[A0=a0i|L0=l0i]，可求出研究对象的逆概率权重。

(3)加权调整。采用第(2)步算得的权重进行加权，采用广义线性模型中的重复测量logit模型分析数据。

结果显示，采用边际结构模型得到的暴露变量的效应值为：OR=0.3798，95%CI：0.2112-0.6828，P=0.0012。而不控制协变量，直接拟合暴露变量和结果变量的logistic 模型得到的暴露变量粗效应值为：cOR=0.4320，95%CI：0.1916-0.9739，P=0.0430。此结果表明，β受体阻滞剂能降低病人术中死亡率，但是，未调整协变量之前，β受体阻滞剂降低术中死亡率的效果被低估了。

6.复杂数据的边际结构模型

当暴露变量为多水平变量(连续或等级)时，当观察性研究中的暴露变量为时间依赖变量时，同样可以基于保守的剂量反应关系构建线性logistic边际结构模型，通过计算平稳权重来控制已观测协变量的混杂影响。当存在删失数据时，把删失也看作是随时间变化的处理，同样可以采用边际结构模型来调整失访所致的偏倚[1-3]。由于本文篇幅有限，在此不作介绍。

讨 论

边际结构模型是近些年新出现的一类因果推断方法。该法与传统因果推断方法有较大区别，它通过构造已观测协变量与暴露变量的模型，通过逆概率权重反映已观测协变量对暴露变量和结局变量的影响，然后根据逆概率权重消除已观测协变量的影响，从而获得暴露变量与结局变量间真实的因果关联[1-2]。

上述实例显示，边际结构模型能很好地控制已测协变量所致的混杂偏倚。Robins等人指出，边际结构模型尤其适合于暴露变量和协变量均为时间依赖变量的观察性研究。由于缺乏此类实例，本文未能介绍此类应用。

参 考 文 献

1. Robins J,Hernán M,Brumback B.Marginal structural models and causal inference in epidemiology.Epidemiology，2000,11(5):550-560.

2.章珏.基于边际均值的多项分布数据的因果效应估计.南京:东南大学,2006.

3.Robins J.Marginal Structural Models versus Structural Nested Models as Tools for Causal Inference.Statistical Models in Epidemiology:The Environment and Clinical Trials.New York:Springer-Verlag,1999:95-134.

4.Rosenbaum P,Rubin D.The central role of the propensity score in observational studies for causal effects.Biometrika,1983,70:41-55.

5.李智文,任爱国.倾向评分法在调整混杂中的应用.詹思延 主编.流行病学进展.第十二卷 .北京:人民卫生出版社,2010:358-376.

6.王永吉,蔡宏伟,夏结来,等.倾向指数第一讲倾向指数的基本概念和研究步骤.中华流行病学杂志,2010,31 (3):347-348.

7.Valle J,Zhang M,Dixon S,et al.Impact of pre-procedural beta blockade on inpatient mortality in patients undergoing primary percutaneous coronary intervention for ST elevation myocardial infarction.Am J Cardiol，2013，111(12):1714-1720.