基于典型相关分析的我国企业技术创新投入与产出的关系研究*

布朝辉，张良强

(福州大学 软科学研究所，福建 福州350002)

1 引言

企业要想在市场中占据主导地位，就需要不断进行技术创新，凭借自身的核心技术占有市场。在一定程度上，企业技术创新产出成果的数量、水平以及技术成果的转化应用情况等都取决于技术创新的投入。

目前，学术界对于企业技术创新投入和产出的研究成果较多。金彦[1]等通过改进知识生产函数对辽宁省企业技术创新投入和科技成果产出两者的关系进行了实证研究，得出辽宁省的技术创新投入对科技成果产出的作用并不稳健和明显;上官小放[2]等利用柯布道格拉斯生产函数对江西省高新技术企业的科技投入和产出中的新产品销售收入进行了分析，他认为经费投入对新产品销售收入的促进作用比人员投入的要大;姜劲[3]和曹勇[4]分别采用协整检验理论和逐步回归的方法对国内高新技术产业技术投入和产出进行了计量分析，验证两者的相关关系。但是，在上述的研究中，由于研究方法所用模型的限制，产出变量只能用一个指标，而技术创新投入产出体系显然是一个多投入、多产出的系统。因此，本文拟对技术创新投入和产出水平从多方面建立指标体系，并建立典型相关分析模型探讨两者之间的关系，从而为企业指明影响技术创新产出的因素，以便使企业采取相应的措施提高技术创新的效率，进而增强企业的技术创新能力。

2 典型相关分析的思路与方法

典型相关分析是用于研究两组变量之间的相关性，反映两组变量之间的相互线性依赖关系的一种统计方法。一般的，为了便于研究两组变量X1，X2，…Xp和 Y1，Y2，…Yq之间的相关关系，通常找出第一组变量的某个线性组合U=a1X1+a2X2+…+apXp和第二组变量的某个线性组合V=b1Y1+b2Y2+…+bqYq，把研究两组变量之间相关的问题转化为研究两个典型变量U与V之间的相关问题，希望使U与V的相关达到最大。我们把基于这种原则的分析方法称为典型相关分析。

一般的，典型变量的对数是根据典型相关系数的显著性检验和典型变量所包含的信息量确定的，各对典型变量本身具有最大的相关性，但与其他对典型变量不相关。其中第一对典型变量(U1，V1)从两组变量提取相关关系的信息量最多，是两个变量组各自的全部变化中最大的一部分共变关系，其相关系数称第一典型相关系数;第二对典型变量(U2，V2)提取的次之，是在两组变量剩余的变化中第二大的共变部分，其相关系数称第二典型相关系数，以此类推，直到两组变量间的相关性被提取完毕为止。这样就可以把原来研究两组变量之间的相关，转化为研究从各组中提出的少数几个典型变量之间的典型相关，从而减少研究变量的个数。

在本文中，我们拟分析的企业技术创新投入和产出都是包括多个表征指标的变量，因此适宜用典型相关分析法进行研究。所以我们对原始数据进行分析，计算出典型相关系数并进行显著性检验，确定出典型变量对数，建立典型相关模型，探讨技术创新投入与产出两者的关系，最后，通过典型相关结构分析与冗余分析对模型分析的科学性进行检验。

3 我国企业技术创新投入与产业关系的典型相关实证分析

3.1 研究变量的确定

3.1.1 技术创新投入变量

技术创新投入可以直接或间接的促进科技的发展，加快经济进步。在本文的研究中，我们将技术创新投入分为四类:第一类是以R＆D经费内部支出(X1)衡量的R＆D资金投入指标;第二类是以技术引进支出(X2)、消化吸收经费支出(X3)、技术改造支出(X4)和购买国内技术经费支出(X5)综合衡量的技术引进消化吸收资金投入指标;第三类是以从事R＆D活动人员数(X6)衡量的科技人员投入水平指标。

3.1.2 技术创新产出变量

企业进行技术创新主要是为了将技术商业化应用，推进企业产品市场化进程，最终获取利润，扩大市场份额。在本文的研究中，我们主要将技术创新产出分为三类:第一类是以专利申请数(Y1)衡量的技术创新技术成果产出;第二类是以新产品销售收入(Y2)衡量的技术创新经济成果产出;第三类是以高新技术产业利润总额(Y3)衡量的技术创新经济效益产出。

3.2 各变量之间的关系分析

为了检验所选取的指标是否可以进行典型相关分析，我们给出两组变量内部各自的相关矩阵，然后给出两组变量间的相关矩阵。从《中国科技统计年鉴》[5]、《中国统计年鉴》[6]中收集指标的原始数据见表1，利用EXCEL中的CORREL函数计算出相关系数矩阵见表2、表3、表4。其中表2是反映企业技术创新投入的组内变量间的相关矩阵;表3是反映企业技术创新产出的组内变量间的相关矩阵;表4是企业技术创新投入和产出组间变量的相关矩阵。

由表2和表3可知，反映企业技术创新投入和产出的指标与组内的指标均呈中高度相关关系，可见对于技术创新投入和产出的指标选取合理，由此确保分析结果的科学性。由表4我们可以看出，企业的技术创新投入和产出这两组变量间存在着中高度的相关关系，所以我们可以构建综合指标来代表这种相关性。也就是说，对于这两组变量，我们能够采用典型相关的方法进行分析。

表1 各指标的原始数据

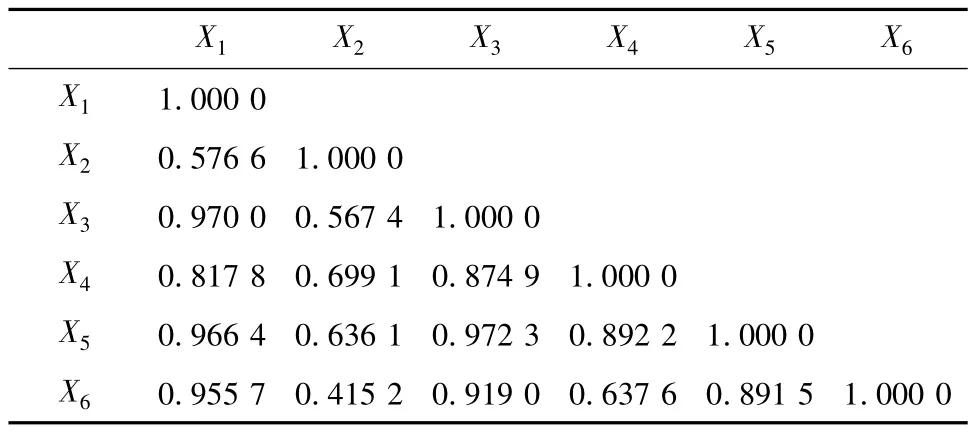
表2 技术创新投入内部指标相关系数矩阵

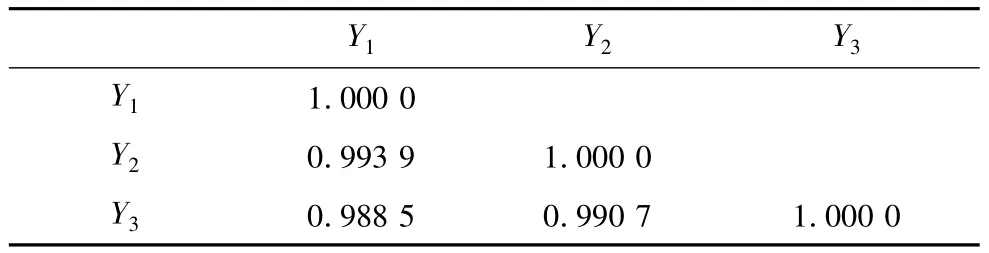
表3 技术创新产出内部指标相关系数矩阵

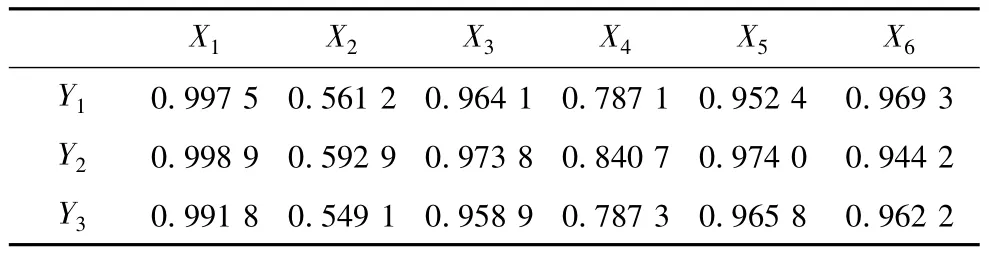
表4 技术创新投入与技术创新产出组间指标相关系数矩阵

3.3 典型相关模型的建立与分析

利用stata软件[7]对数据进行分析，计算出企业技术创新投入和技术创新产出指标的典型相关系数(0.999 9，0.969 7，0.725 5)，为了判断技术创新投入和技术创新产出这两组指标所对应的典型变量是否显著相关，我们对这三个相关系数进行显著性检验，得出三个相关系数在0.01的显著性水平下都是显著的(P＜0.01)，所以企业技术创新投入和企业技术创新产出两组变量相关性的研究可以转化为3对典型变量相关性的研究。

典型相关系数所反映的是在进行典型变式的过程中原始变量的权重，主要是为了说明在构建典型函数的时候，组内变量的相对作用。由于反映指标的原始数据的量纲是不同的，不能进行直接的比较，所以我们在这里所说的典型系数是标准化的系数。所建立的典型相关方程见表5。利用典型相关模型对技术创新的投入和产出的关系进行定量的分析。

表5 典型相关模型

1)由第一组典型相关方程，我们可以看出，在第一典型变量U1中发挥主导作用的是R＆D经费内部支出(X1)，典型载荷为0.813 7，在第一典型变量V1中发挥主导作用的是新产品销售收入(Y2)，其典型载荷为0.584 0，比较重要的是专利申请数(Y1)，其典型载荷为0.429 4。剩下的指标在典型变量的作用并不大。考虑到指标所代表的含义，第一典型变量U1可以用来反映R＆D资金投入，第二典型变量Y2与Y1则分别反映企业的技术创新经济成果产出和技术成果产出。由于三者的典型载荷都为正数，所以，可以得出R＆D资金的投入对于企业的技术创新经济成果和技术成果产出均具有重要的促进作用。

2)由第二典型相关方程，我们可以看出，在第二典型变量U2中发挥主导作用的是R＆D活动人员数(X6)，典型载荷为－2.706 1，在第二典型变量V2中发挥主导作用的是新产品销售收入(Y2)，典型载荷为－10.296 5，此外，R＆D 经费内部支出(X2)在第二典型变量U2中发挥着比较重要的作用，典型载荷为1.425 1，同时在第二典型变量V2中发挥着比较重要作用的专利申请数(Y1)的典型载荷为7.747 1。考虑到指标所代表的含义，第二典型变量U2可以反映科技人员投入，第二典型变量V2可以用来反映企业的技术创新经济成果产出。由Y2和X6两者的典型载荷系数均为负数可知，科技人员的投入对于企业的技术创新经济成果产出具有促进作用。除此之外，由X2和Y1的分析结果可知，第二典型变量还揭示了R＆D资金投入对企业的技术创新技术成果产出具有促进作用。

3)由第三典型相关方程，我们可以看出，在第三典型变量U3中发挥主导作用的是购买国内技术经费(X5)，典型载荷为－6.098 3，在第三典型变量V3中发挥主导作用的是高技术产业利润总额(Y3)，典型载荷为－7.139 1。考虑到指标代表的含义，第三典型变量U3可以反映技术引进消化吸收资金的投入，第三典型变量V3可以用来反映企业的技术创新经济效益产出。由Y3和X5两者的典型载荷系数均为负数可知，技术引进消化吸收资金投入对企业的技术创新经济效益产出具有重要的促进作用。

3.4 典型结构的分析

为了反映原始变量对典型变量的影响程度与方向，我们进行了基于原始变量与典型变量之间的相关系数值的典型结构分析。典型结构分析的计算结果见表6。

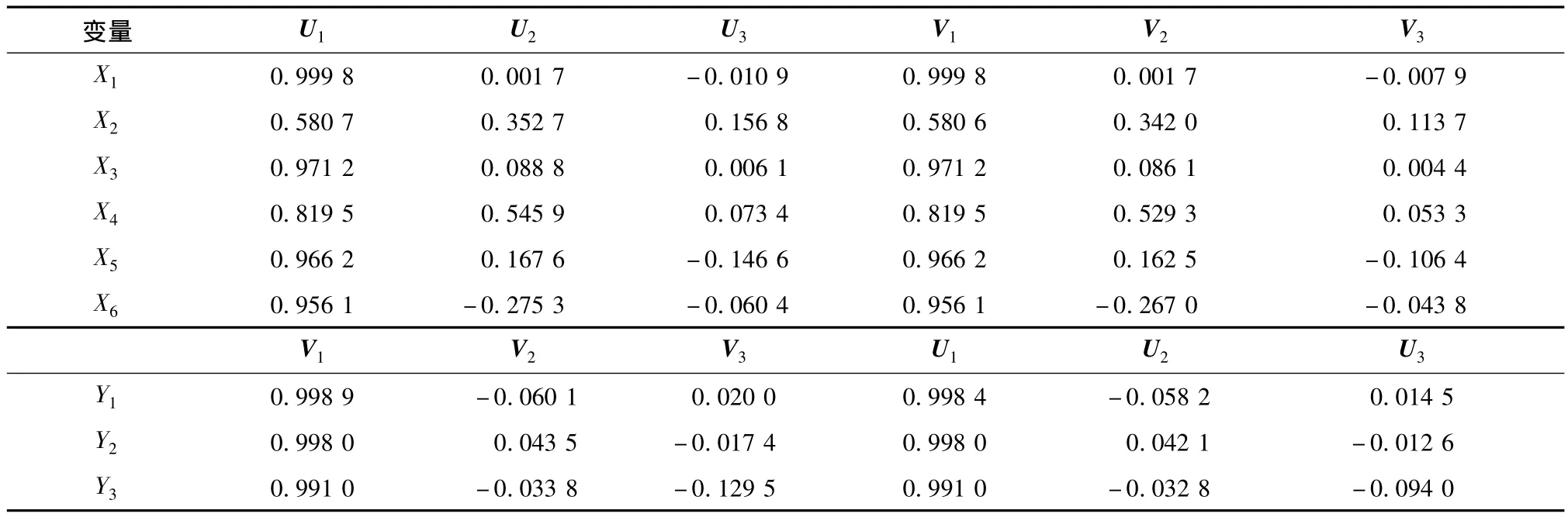
表6 典型结构分析

由表6可知，从整体上来看，技术创新投入组的变量与第一典型变量呈正相关，并且R＆D经费内部支出(X1)与第一典型变量的相关性最高(0.999 8)，可见R＆D资金投入在技术创新投入中占据主导地位。技术创新产出组的变量与第一典型变量呈正相关，并且新产品销售收入(Y2)与第一典型变量的相关性最高(0.998 9)，说明技术创新技术成果产出在技术创新产出中占据主导地位。鉴于第一典型变量之间的高度相关性，导致技术创新投入组的6项指标和技术创新产出组的第一典型变量呈现高度的正相关性，同时技术创新产出组的3项指标与技术创新投入组的第一典型变量也具有高度的正相关性。就各个指标所代表的的含义而言，这样一致的结构揭示了技术创新投入对产出的本质影响。此外，结构分析与典型相关模型间结论的一致性，也证明了典型相关分析结果具有高度的可信度。

3.5 典型变量的冗余分析

一组变量的方差被自身典型变量解释的程度被称为第一典型冗余，而一组变量的方差被对方典型变量解释的程度则是第二典型冗余。为了探究典型变量对其所对应组变量的解释程度，我们对典型变量进行了冗余分析，分析得出两组变量的第一典型冗余分别达到89.8%和99.7%，均高于85%;第二典型冗余也都达到了88.9%和99.9%。可见3对典型变量都很好的预测了对应的那组变量，同时也较好的预测了对方的那组变量，说明技术创新投入和技术创新产出不仅能被自身的典型变量解释，也能够被其对应的典型变量解释。

4 结语

综合上述分析，我们可以得出企业的技术创新投入与技术创新产出存在着显著的相关关系，并且R＆D资金的投入对企业的经济成果和技术成果产出均有明显的促进作用，但是结合典型相关模型1和模型2，可以得出R＆D资金投入对技术成果的产出推动作用更大;人员的投入则会促进经济成果的产出;技术引进消化吸收资金投入则对企业的经济效益产出有着明显的促进作用。

从上面的结论我们可以看出，技术创新投入对技术创新产出有正向的推动作用，但是在上述几个方面的投入上，国内的企业仍有缺陷，据此提出以下几个方面的建议:

1)结合现状，专利申请对企业的技术创新产出水平有着重要的影响作用，所以为加强企业的技术创新能力，一方面要推进专利战略的实施力度，增加R＆D资金投入，大力提高企业的专利开发能力;另一方面，政府部门要为企业提供便利的专利申请服务，同时加强知识产权执法，更好的保护创新企业的利益。

2)就当前国内企业现状而言，许多企业在技术投入上偏重于技术的引进而缺乏技术的自主创新，这样难免会陷入技术的引进、落后、再引进、再落后的恶性循环，无法提高国内企业的生产技术水平。因此，国内企业应该加大技术研发力度，以自主研发为主，引进国外技术为辅，从而步入国际技术的前沿领域，增大自身的竞争力。

3)由于国内企业自身的科研能力有限，所以在加大科研经费的投入之外，还需要加强产学研合作，联合高等院校、科研院所进行技术研发，从而提高企业的技术创新能力。

4)我国的科技人才比较短缺，而这有限的人力资源里仅有1/3的人员参与到了企业的创新活动中[8]。为此，应鼓励并吸引更多的科技人员到企业工作，并鼓励科技人员以成果、专利权入股的形式经营企业，将企业技术创新的风险和他们的利益联系起来，激发科研人员的创新潜能。

[1]金 彦，吴 迪.辽宁省企业技术创新投入与科技成果产出问题研究[J].理论界，2010(7):55－57.

[2]上官小放，贺丹丹，黄子暄.江西省高新技术企业科技投入产出绩效的实证研究[J].金融与经济，2013(8):79－81.

[3]姜 劲，吴 雄.基于高技术创新型企业的创新投入产出研究[J]，数学的实践与认识，2012，42(15):208－213.

[4]曹 勇，苏凤娇.高技术产业技术创新投入对创新绩效影响的实证研究——基于全产业及其下属五大行业面板数据的比较分析[J].科研管理，2008，33(9):23－31.

[5]国家统计局，科学技术部.中国科技统计年鉴[M].北京:中国统计出版社，2001－2012.

[6]国家统计局.中国统计年鉴[M].北京:中国统计出版社，2001－2012.

[7]王大夫，李博柏.STATA实用教程[M].北京:中国人民大学出版社，2008.

[8]赵 梦，梅姝娥，仲伟俊.我国企业技术创新基本状况分析[J].科技与经济，2005，5(18):9 －13.