框架结构损伤定位的比例柔度矩阵分解法试验研究
安永辉, 欧进萍
(大连理工大学土木工程学院, 辽宁 大连116023)
引 言
结构损伤识别的核心问题之一是寻找与结构动力特性密切相关且对损伤敏感的特征参数[1]。结构损伤部位的刚度、强度等力学性能降低,从而导致动力特性发生改变。不同的损伤引起的结构模态参数的改变也不相同,因此可以基于结构模态参数的改变来识别结构损伤[2,3]。柔度矩阵由模态频率和振型构建而成,也集成了这两个模态参数的优点,在基于振动的损伤识别方法中有着较多应用[4~6]。
损伤识别关键要把握两点[7]:第一,选取或构建能反映损伤的特征参数。第二,选取合适的数学工具来处理选定的特征参数使之对损伤更敏感,更好地建立与损伤的联系。这两点直接关系到损伤识别的精度。作者在早期工作中提出了基于柔度矩阵LU分解的损伤定位方法[8],并利用直接识别得到的振型(未进行质量归一化处理)对几个单、多损伤工况进行了初步的数值模拟研究并取得成功。该法从结构振动响应入手,首先识别出结构前几阶模态振型和频率,基于直接识别的模态参数构建结构模态柔度矩阵;然后对损伤前后的柔度矩阵差进行LU分解;最后引入以往在模态振型上使用的曲率法对U矩阵进行处理来构建损伤指标对损伤进行定位。但是严格意义上说,柔度矩阵应该使用质量归一化振型构建,所以基于直接识别振型构建的矩阵不能称为柔度矩阵,并且所提出的方法需要进一步进行试验验证。
由于柔度矩阵由模态频率和质量归一化振型构建而成,这就需要测试结构输入或者需要至少一个测点上同时知道输入和输出才能得到质量归一化振型。但是对于很多工程结构而言,其所受的环境激励等随机激励很难或者无法通过测试得到,导致无法获得质量归一化振型[9]。许多研究者已提出了环境激励下或输入未知时构建柔度矩阵的方法[5,10,12]。其中段忠东等[11,12]提出了测试自由度完备和非完备情况下构建结构比例柔度矩阵的方法,指出比例柔度矩阵与真正的柔度矩阵仅相差一个比例因子。比例柔度矩阵这一概念的提出使得基于柔度矩阵的损伤识别方法可以在环境激励或未知激励的情况下使用。因此,本文将比例柔度矩阵的概念用在提出的损伤定位方法中。获得了结构损伤前后测点的加速度后,可直接构建比例柔度矩阵进行损伤定位:当质量矩阵在各测点处的元素相等时,文中提出了一种简便的构建比例柔度矩阵的方法,其余情况可参考文献[11,12]构建柔度矩阵。该方法不需要建立有限元模型,节省了大量建模和模型修正工作量;同时避免了由于有限元模型中各种不确定因素给结构评估和健康监测带来的影响[13]。
文中首先模拟研究了某20层框架结构在基底白噪声激励下的单、多损伤工况。然后在University of Illinois at Urbana-Champaign设计、建造了一个6层剪切型集中质量框架模型,基于该模型重点进行了其振动台试验和脉冲激励试验下的单损伤和多损伤工况验证,并得出了一些有益的结论。
1 基于比例柔度矩阵LU分解的损伤定位方法
提出的方法基于比例柔度矩阵的LU分解和曲率法,下面给予详细介绍。
1.1 方法的理论基础
1.1.1 比例柔度矩阵的构建
如下方程所示[14],柔度矩阵F可用动力测试模态参数(模态频率和振型)来表示
(1)
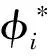
结构质量矩阵为对角矩阵,当质量矩阵中各测点位置对应元素相等时,假设其质量矩阵为
M=μI
(2)
式中μ为常数,I为维数与M相同的单位阵。假设直接识别得到的振型与质量归一化振型之间的关系为
(3)
式中κi为常数。结构的质量归一化振型φi可通过下式求得
(4)
将式(2),(3)带入式(4)可得
(5)
所以可求得
(6)

(7)
将式(3)带入式(1)可得结构的真实的柔度矩阵F为
(8)
假设质量矩阵M=I,即μ=1时结构的比例柔度矩阵Fp为
(9)
比较式(8)和(9),可得两个柔度矩阵之间的关系为
Fp=μF
(10)
可知两者之间只相差一个比例因子μ,并且与文献[11,12]指出的该比例常数为结构的第一阶模态质量这一结论保持一致。
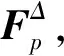
(11)
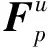
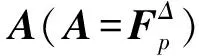
(12)
得到U矩阵后,对于m×m维的U矩阵,定义向量UU为矩阵U的每列元素的平方和,即
(13)
式中符号“.*”指点乘,即将该符号前后两个矩阵对应位置元素相乘。
1.1.3 基于向量UU曲率的损伤指标
曲率模态法由Pandey等[17]于1991年提出,之后研究者基于该法做了很多研究,证明了曲率方法对损伤的敏感性。对位移模态进行“中心差分”后得到振型的曲率为[17]
(14)
式中v为模态位移,h为数值模型中的单元长度。
目前,曲率方法已经成为损伤识别领域的一个基本数学工具。类似地,本文定义向量UU的“曲率”如下
(15)
式中Ck是节点k处的曲率,(UU)k是矩阵UU的第k个元素。
为方便在图中观察,定义损伤指标DI如下
DIk=(Ck)*
(16)
式中 (Ck)*为Ck的归一化值,即将最大值变为1。
1.1.4 比例柔度矩阵对损伤指标的影响
下面简要讨论一下基于柔度矩阵和比例柔度矩阵对文中提出的损伤指标DI有何影响。
基于真正的柔度矩阵差FΔ进行损伤定位时,
(17)
对FΔ进行LU分解,结果见下式
(18)
记此时向量UU为UU*,
(19)
由于UU和UU*是成比例的,则根据式(15)计算出的向量UU和UU*的曲率在每个测点处也是成比例的,并且比例因子相同;但最终的损伤指标,即向量UU和UU*的归一化曲率则相同。所以基于比例柔度矩阵和基于真正的柔度矩阵进行损伤定位时,提出的方法中最终的损伤指标是相同的,损伤定位结果也是相同的。
1.2 方法的步骤
1)获得结构损伤前后测点的振动响应;
2)基于NExT-ERA法(针对环境激励)或者ERA法(针对脉冲激励)等参数识别方法识别结构的前几阶模态参数;
3)构建质量归一化振型,对于文中结构或常见的质量均匀分布的结构,可假设其质量矩阵为单位阵进而获得假设情况下的质量归一化振型进而构建损伤前后的比例柔度矩阵;其他情况下的比例柔度矩阵构建参考文献[11,12];
4)对比例柔度矩阵差进行LU分解;
5)获得向量UU;
6)计算向量UU在各个测点处的“曲率”并将曲率值对其最大值归一化,其中正向突起处与损伤位置相关;
7)为了减弱噪声及模态识别的不确定性对损伤识别结果带来的影响,采用多组不同的数据按照前6个步骤进行多次识别,取多次识别结果的平均值作为最终损伤识别结果;尤其对小损伤,将多次识别结果的平均值作为最终结果可较大提高损伤识别准确率。
2 数值验证
2.1 数值模型
为了检验提出方法的有效性,选取某20层集中质量剪切型框架结构(图1)作为研究对象进行数值模拟验证:该结构中ki=600 kN/m,mi=500 kg,i=1,2,3,…,20,阻尼比ζ=0.02,获得刚度矩阵K和质量矩阵M后,Rayleigh阻尼矩阵C可由K,M求出,则结构基本运动方程为
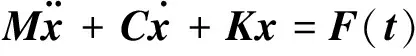
(20)
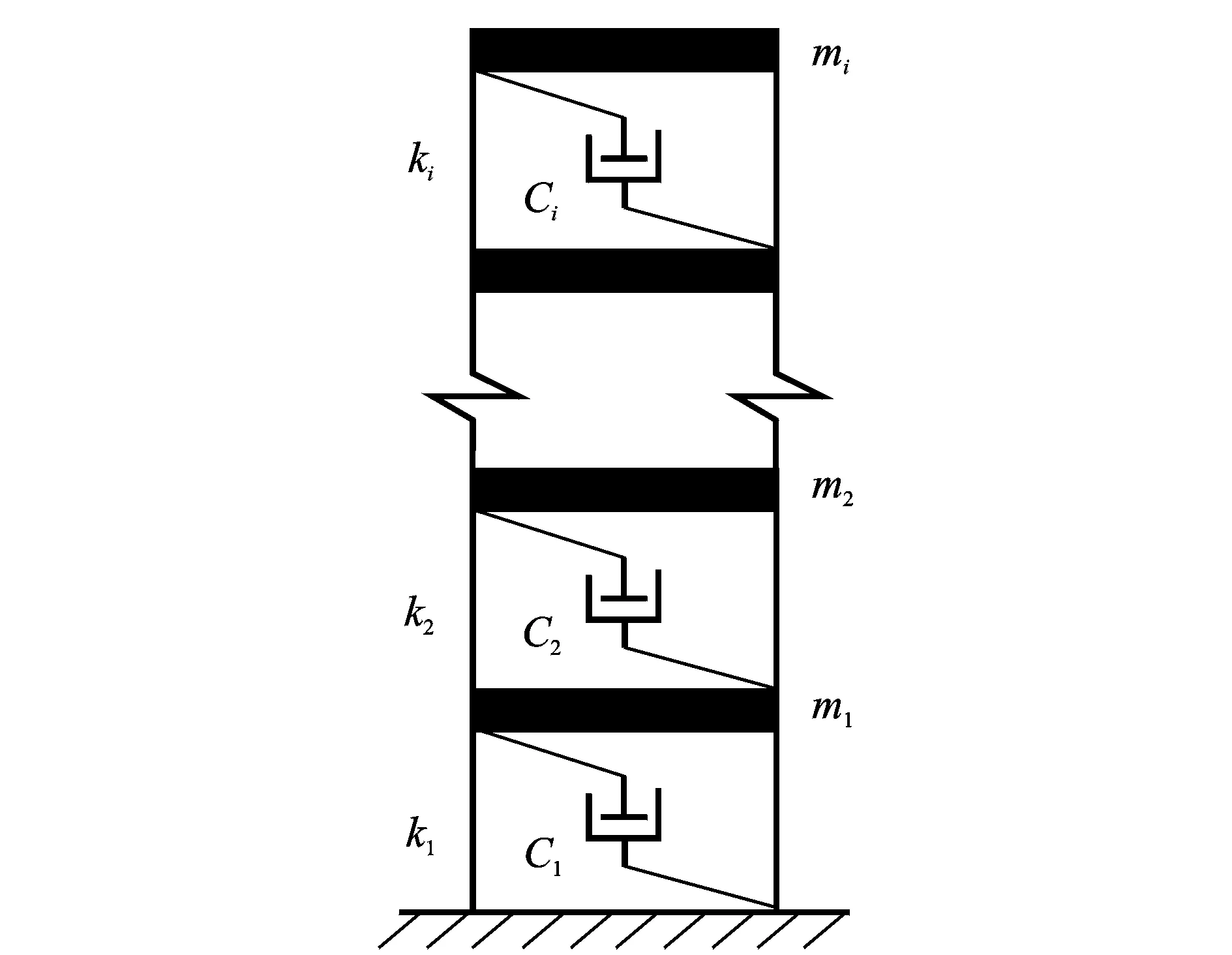
图1 某20层剪切型框架结构
基底随机激励下结构的状态空间矩阵As,Bs,Cs,Ds可用下列式子表示
式中As为系统矩阵,Bs为输入矩阵,Cs为输出矩阵,Ds为直接传递矩阵。
脉冲激励下该结构的状态空间矩阵中As和Cs不变,Bs和Ds如下:
式中G为脉冲激励输入位置向量,没有激励的自由度处G元素为0。
获得结构的状态空间矩阵As,Bs,Cs,Ds后,可在SIMULINK里建立不同激励形式下相应的结构模型来获得加速度响应。需要注意的是SIMULINK里通过Band-limited white noise模块来施加随机激励来模拟环境激励,为了使损伤前后的随机激励不同,需在这个模块里设置不同的seed。损伤通过折减某层的刚度k来模拟,在损伤前后各测点的加速度响应里加入5%的噪声模拟测试误差及环境噪声。
2.2 损伤工况及结果
本文侧重于试验验证,数值模拟部分仅以基底白噪声激励(模拟环境激励)下的三个损伤工况为例来进行验证。如表1所示,三个损伤工况分别为单损伤、双损伤和三损伤工况。

表1 数值损伤工况
获得各损伤工况中损伤前后的加速度响应后,假设结构质量阵M为单位阵对识别振型进行处理,选取结构前4阶振型,然后按照1.2节提出方法的具体步骤进行10次损伤识别并取平均值,最终的损伤定位结果分别如图2,3,4所示,图中第二部分为第一部分中的正值部分的直方图。
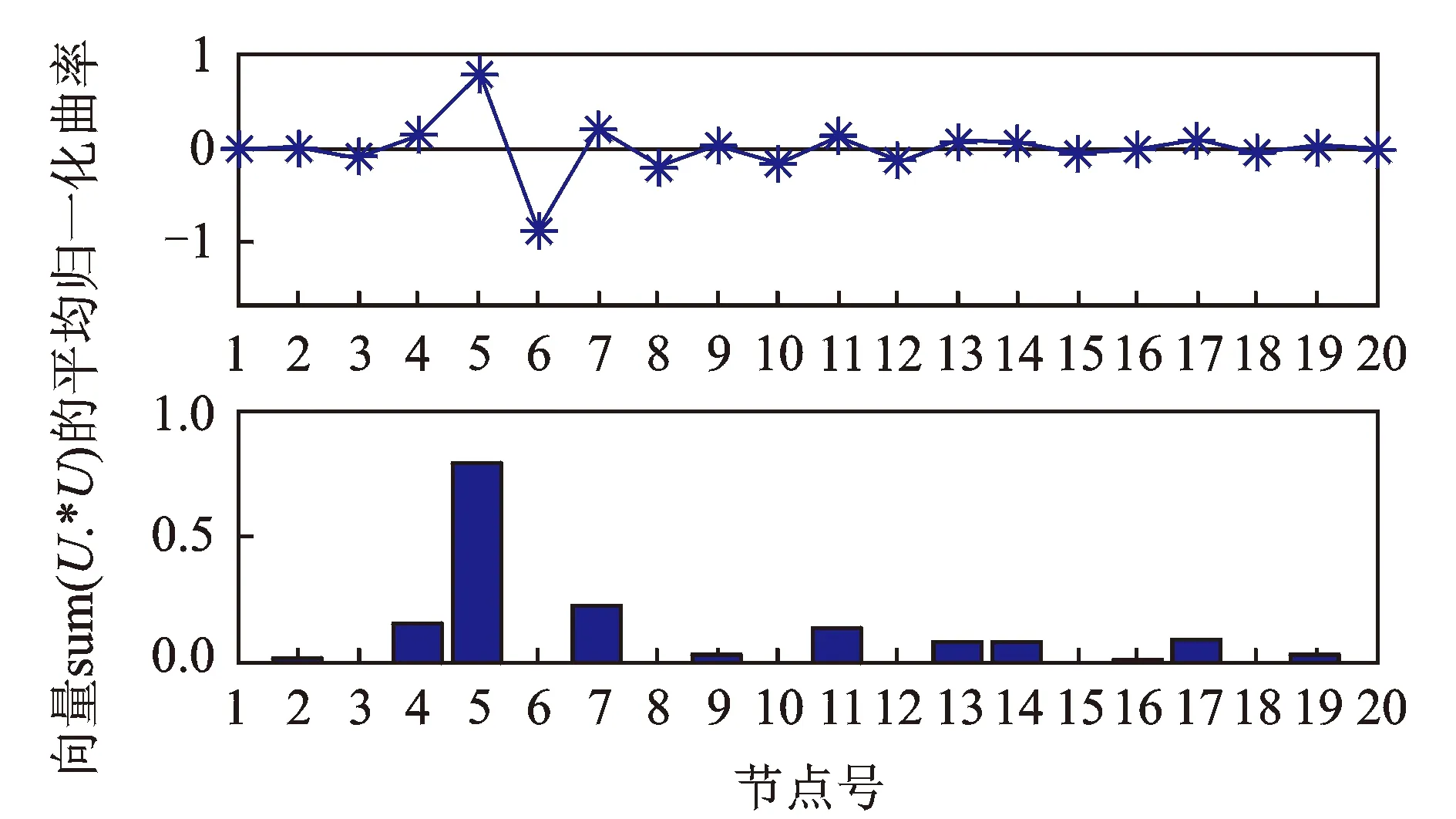
图2 5%噪声下损伤工况S1数值模拟结果
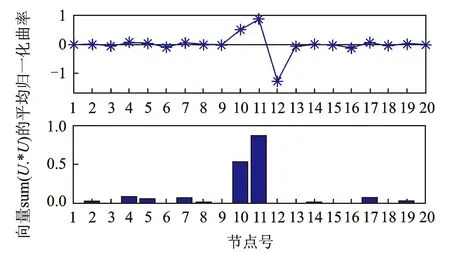
图3 5%噪声下损伤工况S2数值模拟结果

图4 5%噪声下损伤工况S3数值模拟结果
从图2,3,4中可以看出无损伤处的损伤指标(即归一化曲率)接近于0;同时从图2可知当第6层损伤时,节点5和6处的损伤指标值明显突起,其中5处正向突起;图3可知当第11,12层损伤时,节点10,11处的损伤指标值明显正向突起,12处的损伤指标值负向突起;图4可知当第5,10,18层损伤时,节点4,9,17处的损伤指标值明显正向突起,5,10,18处的损伤指标值负向突起。以上结果及未列举出的大量的数值模拟结果均呈现相同的规律:节点(x-1)处的损伤指标值正向突起代表结构第x层损伤。至此,无论单损伤还是多损伤工况的数值模拟结果均成功定位了预设损伤。
3 试验验证
为了进一步试验验证提出方法的可行性,在美国University of Illinois at Urbana-Champaign的智能结构技术实验室里设计、建造了一个6层剪切型集中质量框架模型,如图5所示。该框架层高为210 mm,宽度为260 mm,每层的弹簧钢柱子的尺寸为50 mm×1.27 mm,每层的集中质量(包括塑料梁、钢块、螺钉)为2.17 kg。经过模态试验测试,该模型的前6阶固有频率依次为1.72,5.16,8.34,11.06,13.19,14.59 Hz。预备几个厚度稍小(也是美国钢板标准厚度之一)、其余尺寸不变的柱子作为损伤柱,试验中通过将某层柱子更换为损伤柱来模拟该层的损伤。

图5 试验模型及振动台
3.1 试验设备
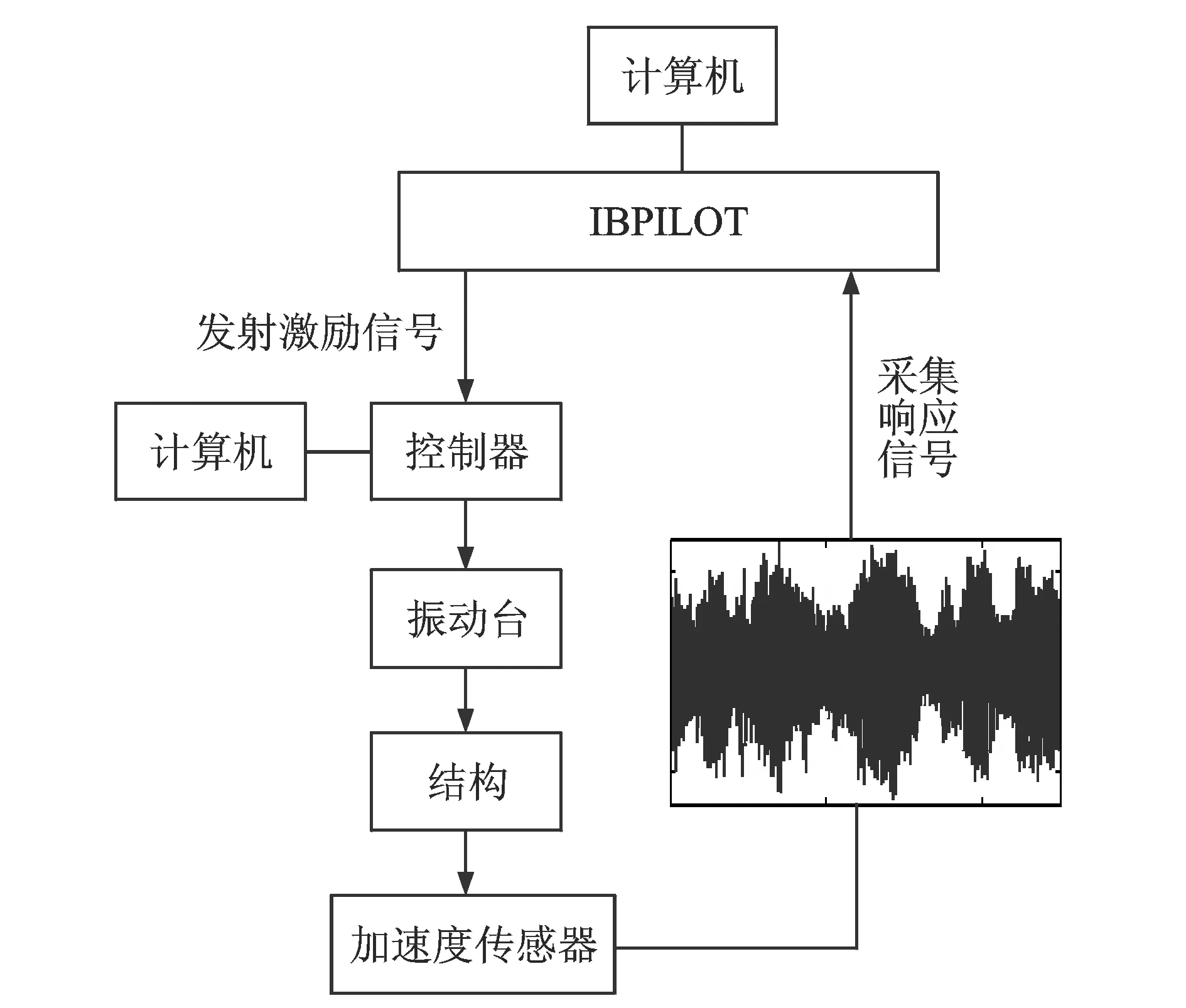
图6 地震台试验各设备连接示意图
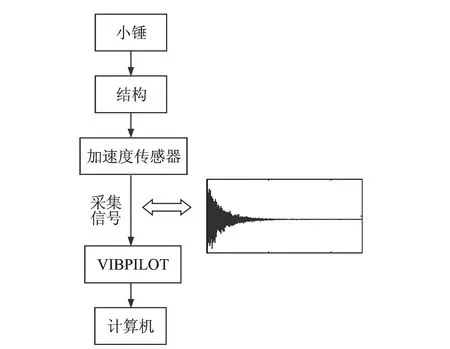
图7 小锤脉冲激励试验示意图

图8 VIBPILOT仪
采用两种不同形式的试验激励方式来验证提出的方法,图6,7所示分别为地震台试验和脉冲激励试验中各设备和仪器之间的连接示意图。图8所示为VIBPILOT信号发射与采集仪,它既能产生信号并通过控制器输送给振动台,同时又能采集模型的振动响应;试验采集过程中采用Butter低通滤波对数据进行处理,截止频率为15 Hz,加速度传感器的灵敏度约为100 mV/g。
3.2 试验工况及结果
如表2所示,8种试验工况用来进一步验证提出的方法在不同激励下的损伤定位效果。基于前述方法对每个损伤工况进行识别。
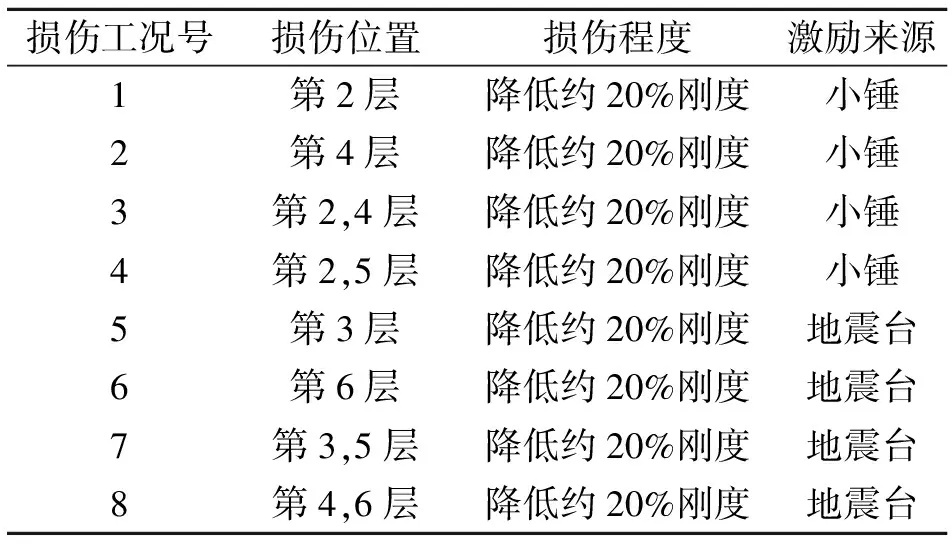
表2 试验损伤工况
单次损伤识别试验结果如图9所示,根据数值模拟结果呈现的规律来确定损伤位置:当结果为节点(x-1)处损伤指标正向突起时,结构第x层损伤;图9所示试验结果均成功定位出损伤层。不同激励下的单损伤和多损伤工况试验结果进一步验证了所提出的损伤定位方法可以准确地对损伤进行定位,并且该法不受激励形式的影响,只要模态参数识别准确,损伤定位结果就准确。同时试验发现,若用直接识别振型构建柔度矩阵,识别效果不好甚至错误。
4 结 论
本文提出了基于比例柔度矩阵LU分解和曲率的损伤定位方法,并通过大量的数值和试验工况对这个新方法进行了模拟和试验验证,主要结论如下:
1)文中研究了不同激励形式下的单损伤和多损伤工况,数值和试验结果均表明提出的损伤定位方法能对损伤进行准确地定位;噪声水平5%下,该方法可对单元刚度降低10%的小损伤进行准确定位。
2)文中提出的损伤定位方法可适用的结构激励方式多样,可以是环境激励、脉冲激励、基底随机激励等,并且不需要测量输入,可用于结构实时健康监测和定期检测。
3)当质量阵的各测点处对应元素相等时,还提出了一种简便的构建比例柔度矩阵的方法。
4)文中提出的损伤定位方法只需损伤前后的振动响应数据,不需要结构有限元模型,避免了复杂的数值模型建模及模型修正工作;并且构建一个满足精确度的柔度矩阵只需要结构的前几阶低阶模态参数,这些参数基于目前的参数识别技术便可得到较为准确的识别,这些优点均为该方法的工程应用奠定了基础。
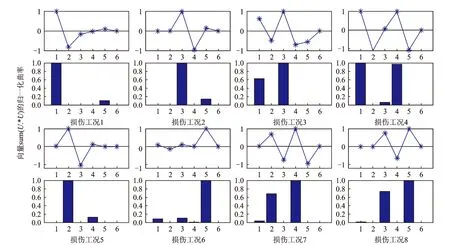
图9 8个试验损伤工况的损伤定位结果
致谢本文试验模型为第一作者在University of Illinois at Urbana-Champaign建立,该模型得到了B F Spencer,Jr教授的经费资助,在此表示衷心的感谢!
参考文献:
[1] 林友勤,任伟新.基于随机状态空间模型的工程结构损伤检测 [J].振动工程学报,2007,20(6):599—605.Lin Youqin, Ren Weixin. Stochastic state space model-based damage detection of engineering structures[J]. Journal of Vibration Engineering, 2007,20(6):599—605.
[2] 张育智,李乔,单德山.SOFM网络在结构损伤位置识别中的应用[J].振动与冲击,2007,26(2):160—163.Zhang Yuzhi, Li Qiao, Shan Deshan. Application of SOFM network for structure damage location identification[J]. Journal of Vibration and Shock, 2007,26(2):160—163.
[3] 李睿,于德介,曾威.模式密度方法在结构异常检测中的应用研究[J].振动工程学报,2008,21(4):343—348.Li Rui, Yu Dejie, Zeng Wei. Application of structural damage diagnosis using density-based outlier detection[J]. Journal of Vibration Engineering, 2008,21(4):343—348.
[4] 于德介,雷慧,程军圣.基于BP神经网络与柔度变化的结构破损诊断[J].振动工程学报,2001,14(3):345—348.Yu Dejie, Lei Hui, Cheng Junsheng. A method for structural damage detection based on back propagation neural network and flexibility changes[J]. Journal of Vibration Engineering, 2001,14(3):345—348.
[5] Gao Y, Spencer B F Jr. Damage localization under ambient vibration using changes in flexibility[J]. Earthquake Engineering and Earthquake Vibration, 2002,1:136—144.
[6] Bernal D. Flexibility-based damage localization from stochastic realization results[J]. Journal of Engineering Mechanics, 2006,132(6):651—658.
[7] An Y H, Ou J P. Experimental and numerical studies on model updating method of damage severity identification utilizing four cost functions[J]. Structural Control and Health Monitoring, 2013,20:107—120.
[8] An Y H, Ou J P. Use of LU decomposition of modal flexibility in structural damage detection: numerical validation[J]. Key Engineering Materials, 2013,569/570:986—993.
[9] Ni Y Q, Zhou H F, Chan K C, et al. Modal flexibility analysis of cable-stayed ting kau bridge for damage identification[J]. Computer-Aided Civil and Infrastructure Engineering, 2008,23:223—236.
[10] Yan A M, Golinval J C. Structural damage localization by combining flexibility and stiffness methods[J]. Engineering Structures, 2005,27:1 752—1 761.
[11] 段忠东,闫桂荣,欧进萍,等.结构比例柔度矩阵[J].哈尔滨工业大学学报,2006,38(8):1 236—1 238.Duan Zhongdong, Yan Guirong, Ou Jinping, et al. Proportional flex ibility ma tr ix of structures[J]. Journal of Harbin Institute of Technology, 2006,38(8):1 236—1 238.
[12] Duan Z D, Yan G R, Ou J P, et al. Damage detection in ambient vibration using proportional flexibility matrix with incomplete measured DOFs[J]. Structural Control and Health Monitoring, 2007,14:186—196.
[13] 杨海峰,韩晖,吴子燕.基于MIGA的结构模型修正及其应用[J].振动、测试与诊断,2012,32(2):261—266.Yang Haifeng, Han Hui, Wu Ziyan. Structure model updating based on miga and its application[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(2):261—266.
[14] Pandey A K, Biswas M. Damage detection in structures using changes in flexibility[J]. Journal of Sound and Vibration, 1994,169(1):3—17.
[15] Juang J N, Pappa R S. An eigensystem realization algorithm for modal parameter identification and model reduction[J]. Journal of Guidance, Control, and Dynamics, 1985,8(5):620—627.
[16] James G H, Carne T G, Lauffer J P. The natural excitation technique (NExT) for modal parameter extraction from operating structures[J]. Journal of Analytical and Experimental Modal Analysis, 1995,10(4):260—277.
[17] Pandey A K, Biswas M, Samman M M. Damage detection from changes in curvature mode shapes[J]. Journal of Sound and Vibration, 1991,145(2):321—332.

