基于序贯高斯模拟的储量估算分层更新技术
李 迪,胡乃联 ,李国清,侯 杰
(北京科技大学金属矿山高效开采与安全教育部重点实验室,北京 100083)
矿产资源储量是矿山的生命线,也是矿业项目评价、矿床开发和矿山生产中最主要的指标之一[1-2]。精确估算矿产储量对矿山生产管理和规划具有重要的指导意义,目前矿山通常采用具有无偏估计的克里格法进行储量估算。
随着矿山实际生产,将产生海量炮孔岩粉数据,这些高密度数据的加入能够大幅提高储量估算精度。为此,迫切需要将储量估算模型进行更新。更新后的模型用于指导矿山实际作业,如配矿、开采设计、选矿等后续工作,因而需要模型的品位分布有高度准确性。然而,储量估算是以地质勘探数据为基础的静态计算过程,其更新问题极其复杂,原因如下:其一,炮孔岩粉数据与用于初步估值的地质钻孔数据网度、样长不同,如何进行有效融合需要系统讨论;其二,常规估值方法有诸多弊端,如距离幂次反比法缺乏考虑地质因素,克里格法带有平滑效应,均不能较好的模拟实测数据的品位分布及其空间自相关性,需寻求新方法;其三,储量估算流程相对固定和复杂,地质工作者主观决策因素较多,使得模型便捷更新较为不易。为此,本课题采用常用于储层建模的条件模拟方法,并以国内某大型露天钼矿为工程背景尝试其在矿床储量模型更新中的应用。
1 常用储量估算方法及分析
储量估算方法有很多,大体包括传统方法、SD法以及地质统计学方法等。近年来,随着神经网络、遗传算法、分形等理论迅速发展,相继出现结合这些理论的新兴估值方法。在众多估值方法中最常用,并广泛引入矿业软件的有距离幂次反比法与克里格法[3]。
距离幂次反比法以其原理简单、插值过程快速高效的特点,广泛应用于各领域[4]。国内外诸多软件引入距离幂次反比法作为内部插值计算方法,如矿业软件3Dmine、MicroMine、Surpac,遥感软件ERmapper[5]及统计分析软件等。距离幂次反比法是一种常用而简便的空间插值方法,它以插值点与样本点间的距离为权重进行加权平均。然而该方法单单只考虑了距离与待估值之间的关系,并没有考虑到空间地质因素所造成的空间相关性,具有一定的弊端。为提高估值精度,人们广泛应用地质统计学中经典的克里格法进行估值。
克里格法是以矿化空间结构理论为基础,区域化变量为核心,变异函数为工具的数学地质方法,是地质统计学中的核心方法,在国内外各学科领域有着广泛的应用。在矿业领域,地质统计学不仅广泛应用于资源储量计算,在其他矿业活动,如异常评价[6]、找矿勘探[7]、矿体圈定[8]及采矿设计[9]等方面也具有明显的优越性。
克里格法遵循无偏估计和最优估计原则,在插值计算中引入区域化变量理论,因而估算精度相对较高,对于整个矿体的储量估算工作,只要求得到矿床储量而言,是相对合理的方法。然而,该方法的缺陷是其平滑效应[10],这种平滑效应使得矿石品位均化,不能完好的再现具体的品位分布及波动,因而对指导矿山具体配矿、开采设计等相关具体作业的储量更新工作而言,精度欠佳。
2 基于序贯高斯模拟的动态更新技术
条件模拟技术是地质统计学继克里格族群之后,迅速发展的一个新分支,它的结果是每个待估点的可能取值以及其发生的条件概率,该方法并完全尊重于实测数据。随着条件模拟各种方法的出现和不断完善,其技术在许多方面都得到广泛的应用。条件模拟技术最初由A.Journel教授在他的著作“矿业地质统计学”中提出并详细地阐述其基本概念和算法,其后在此基础上很多新算法相继出现,如LU三角矩阵分解法、序贯高斯模拟、序贯指示模拟及分形模拟等方法。目前,条件模拟主要在石油储层建模方面的得到广泛应用,如使用条件模拟方法解决确定沉积相带的空间分布[11],以及模拟非均质石油储层建模等等。另外,条件模拟的发展还体现在了一些非地质领域,如水土科学、森林资源评估等。
条件模拟在许多领域都取得了一些进展,但目前在矿山方面的应用较少,需要进一步研究。
2.1 序贯高斯模拟的基本原理
条件模拟的方法有很多,其中序贯高斯模拟能正确反映区域化变量的空间波动特点,能再现真实资源特性空间变异曲线的波动,是条件模拟中的首选算法。其特点是随机抽取样本模拟后将模拟值最为下次模拟的条件,序贯虑每个网格节点直到所有点模拟结束,下面简述其基本原理。
正态得分变换:由于序贯高斯模拟严格要求数据服从高斯分布,因而需将不满足条件的数据进行正态得分变换,模拟后再将数据逆变换。
随机变量Z(u),给定n个数据条件,则其条件累积分布函数(ccdf )为
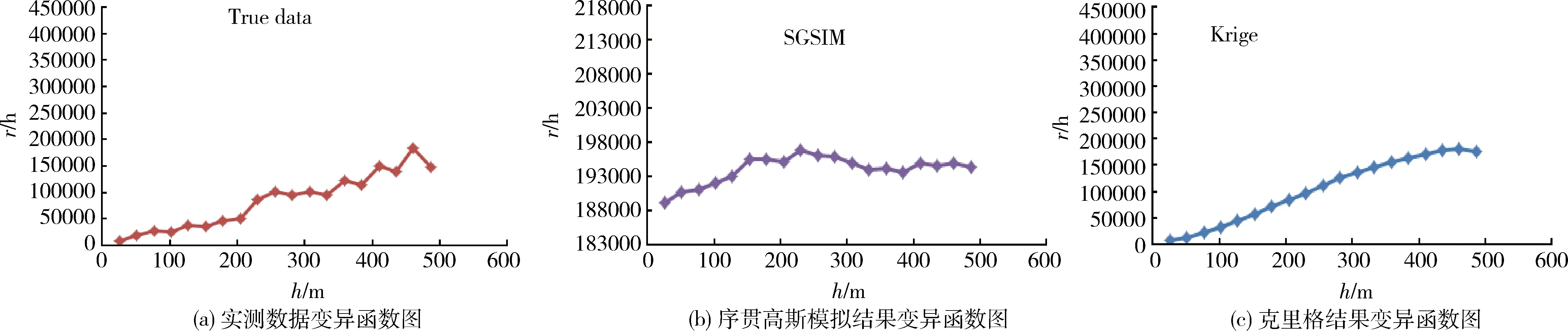
Fz(z|(n))=Prob{Z (1) 序贯高斯模拟严格要求数据服从高斯分布,因此FZ(z)需进行正态变换.若其累积分布函数FY(y)为标准高斯累积分布函数G(y),即有正态变换 (2) 对n个Z(u)采样的观测数据以单增排列,则有相应于第k个Z值的累积频率,Zk的正态转换就是标准正态分布函数的分位数,即 (3) 模拟原理:设爆区品位数据Z(u)为满足二阶平稳假设的区域化变量,在空间任一点u处的真实值可表示为普通克立格估值Zk×(u)与其偏差之和,即 (4) 两者具有相同的数学期望、协方差和变差,Zsk×(u)为Zs(u)的克立格估计值.由于Zs(u)与Z(u)同构,Zsk×(u)与Z×(u)同构,则其克立格方程组相同,其权系数解λi也应相同[12],即有 (5) 则在实测点ui要求模拟值等于观测值条件下,点u处Z(u)的条件模拟值Zsc(u)可表示为非条件模拟Zs(u)与其在各实测点偏差的克立格估计值之和,即 Zsc(u)=Zs(u)+∑λi[Z(ui)-Zs(ui)] (6) 其中,Zs(u)和Zs(ui)可通过随机抽样方法得到。 由上述原理可知,序贯高斯模拟值实际上是克里格插值结果与期望为0,方差等于克里格方差的随机偏差之和。多次随机模拟的平均值无限趋近克里格插值结果。然而克里格插值是使用已知点数据估计未知点,而序贯高斯模拟的每一次计算都加将之前模拟的数值作为已知条件加入计算,因而建立了数据的全局相关性,这是条件模拟能再现实测数据分布的根本原因。 克里格法的特点在于无偏性和估值误差方差最小,但却导致平滑效应,使得对全局的空间变异程度的估计偏低。因此,本文认为克里格法应主要用于计算平均结果,如初步求解矿体储量;而序贯高斯模拟保持了全局空间变异性,并在每个待估点提供任意多个可能性,虽然任一次的模拟结果较克里格插值的可信度差,但由于取值的随机性,多次模拟可提高其估值精度,因而更适合指导具体作业的储量更新模型,体现数据的整体分布。 本课题以国内某大型露天钼矿为工程背景研究序贯高斯模拟在储量估算模型更新中的应用。该矿区采矿权面积4.6 km2,开采深度由640m至0m标高,为目前国内最大单一钼矿床。矿区最主要的Ⅰ号矿体工业矿钼资源矿量79504.75万t,金属量717662.90t,平均品位0.090%。针对资源特点,采用露天开采方式,以15m为台阶高度进行分层剥离。 工程应用的基本思路如下:首先根据矿山地质钻孔数据建立矿床资源模型,并采用对数克里格法进行初步储量估算,随后加入生产中周期性产生的炮孔数据,将地质钻孔与生产爆破数据融合,并采用序贯高斯模拟法计算储量,最后以爆区为单位逐步计算,代替初步储量估算模型,以达到逐渐更新模型,提高精度的目的。技术路线图见图1。 图1 技术路线图 初步储量估算以地质勘探钻孔数据为基础借助矿业软件SURPAC进行插值计算。本次储量估算共收集到173个钻孔,勘探网度为100m×100m,其中测斜数据736行,岩性数据1596行,品位化验数据27942行,按照数据格式生成钻孔数据库。经统计,钼品位化验数据最小值为0,最大值为24790,均值为519.88,标准差为778.684,变异系数为1.498,偏度为6.60,峰度101.127,其频率基本符合对数正态分布。随后根据国家相关标准及该矿相关指标圈定矿体实体模型,如图2所示。初步储量估算采用无偏估计的克里格法进行计算,首先将实体内钻孔数据进行组合,组合样长2m,而后进行变异函数的拟合及对数克里格插值计算最后将对数组合样进行转化,估值结果如图3所示。 图2 矿体三维实体模型 图3 估值后矿体品位分布 为提高储量估算及品位分布精度,必须充分利用矿山化验数据,如已有地质钻孔数据及阶段性供给的加密炮孔岩粉数据对矿床模型进行更新计算。由于炮孔数据以台阶爆破为单位,样长均为15m,因此选用15m台阶高度为单位分层对模型进行更新较为合理。这里将原样长为2m的地质钻孔以台阶高度标高为基准,15m为样长进行样品组合,而后融入炮孔数据,对模型进行更新。由于更新后的模型用于指导矿山后续配矿、境界优化、开采设计等实际工作,要求矿石品位分布的高度准确性,这里采用能够真实还原全局空间变异性的序贯高斯模拟算法进行矿床三维模型的分层更新。 本研究使用SGeMS软件中的序贯高斯模拟模块对生产勘探的炮孔数据进行插值更新。SGeMS(Stanford Geostatistical Modeling Software)[13]是美国斯坦福大学开发的一套地质统计学程序库,其包含了地质统计学中绝大多数算法,包括多种克里格估值模块,条件模拟模块等。 数据以该矿495-510台阶爆破数据为例进行研究,并根据6m×6m爆破网度以及15m台阶高度,建立6m×6m×15m的块体。经统计,钼品位化验数据共227个,均值654.653ppm,方差189755,最大值2960最小值0,中位数580,其空间分布如图4所示。 图4 爆区散点分布图 为得到模拟搜索椭球体参数,需将数据进行变异函数的拟合。搜索展开角选择22.5°,生成变异函数曲线。由于组合数据为水平层状数据,因而其短轴没有数据,次主轴只在0度附近有少量数据。经变异函数拟合后得到块金值为100958,方位角139.56,倾角0°,变程138.95的椭球体搜索参数,其主轴拟合过程见图5。序贯高斯模拟的前提是数据服从高斯分布,因此需将数据进行正态得分变换,而后将拟合参数带入SGeMS运行序贯高斯模拟模块对数据进行插值计算,模拟启动源随机产生为14071788,最后将得到的结果进行正态变换的逆运算。序贯高斯模拟结果如图6所示。 图5 变异函数拟合 图6 序贯高斯模拟结果 最后按照台阶爆破周期将炮孔数据进行序贯高斯模拟,并通过实体约束将模拟结果与初步模型导入Surpac自由变量块体进行块体融合与更新。这里得到的更新后模型是由两种块度构成的,分别是基于原地质数据的12m×12m×15m的块体以及基于炮孔数据的6m×6m×15m的块体,实现了不同块度、不同数据来源、不同储量级别的更新块体,见图7。随着台阶爆破的进行,得到逐步精确的储量值及品位分布。 图7 更新后的模型 为进一步分析拟合结果,这里针对同一组爆破数据进行克里格估值,并将序贯高斯模拟得到的结果与克里格插值结果进行对比,频率直方图如图8所示。 由图8可知,序贯高斯模拟与实测数据的频率直方图基本一致,体现了序贯高斯模拟与实测数据具有相同的空间自相关结构,更能正确反映品位数据空间波动特点。然而克里格估值使得估值结果过于集中,平滑效应明显,不能真实再现实测数据的品位分布。从这一角度看,序贯高斯模拟的预测结果可信度更高。 从变异函数角度看(图9),序贯高斯模拟的变异函数曲线的变化趋势更接近实测数据一些,但其变异函数值与实测数据相比有一定差距,即方差较大。相反,克里格估值的变异函数曲线变化趋势与实测数据有明显不同,然而其方差却比较小。该组折线图反映了序贯高斯模拟方法能更好的显示品位空间变异性,但与克里格法相比方差较大的特点。 图8 序贯高斯模拟与克星格法对比直方图 图9 序贯高斯模拟与克星格法变异函数对比 本文结合矿山实际需求,针对常规储量估算工作并不能充分利用有效数据的现状,提出采用序贯高斯模拟算法加入炮孔数据进行矿床模型的分层更新,并以国内某大型露天钼矿为例进行验证,得出如下结论。 1) 炮孔岩粉数据较地质钻孔数据网度大幅加密,将两种数据融合,充分利用有效数据是提高储量估算精度的基础。 2) 加入岩粉数据的模型分层更新结果用于指导矿山的配矿等实际生产,因而采用更能反映数据全局变异性及波动性的序贯高斯模拟算法更为恰当。 3) 序贯高斯模拟相比于克里格算法更能体现实测数据的空间自相关性与变异性,即全局数据分布的准确性,但其局部方差略高于克里格算法,多次模拟可提高精度。 [1] 谈树成,虎雄岗,金艳珠,等.基于地统计学与GIS的固体矿产资源储量估算方法研究[J].中国矿业,2013,3(22):101-105. [2] 陈国旭,田宜平,刘刚等.资源储量估算、图表编制一体化与可视化系统研究[J].金属矿山,2009,394(4):102-108. [3] 张伊丽.基于CUDA的泛克里格算法的研究与设计[D].北京:中国地质大学(北京),2012. [4] 牛文杰.基于变异函数的距离加权反比法[J].东华大学学报:自然科学版,2011,37(3):362-367. [5] 丁建华,肖克炎,娄德波,等.大比例尺三维矿产预测[J].地质与勘探,2009,45 (6):729-734. [6] 韩天成,张振飞,吕新彪,等.东天山中段区域化探异常评价方法研究[J].地质与勘探,2011,47(5):885-893. [7] 陈道贵,李建锋,郭秀峰.基于克里格方差的勘探/取样网度优化[J].现代矿业,2012,27(7):43-46. [8] 尤超,张唯,刘修国.指示克里格法在矿体圈定中的应用研究[J].信阳师范学院学报:自然科学版,2012,25(1):130-132. [9] 王斌,刘保顺,王涛.基于Surpac的矿山三维可视化地质模型的研究与应用[J].中国矿业,2011,20(2):106-109. [10] 李晓晖,袁峰,贾蔡,等.基于地统计学插值方法的局部奇异性指数计算比较研究[J].地理科学,2012,32(2):136-141. [11] 于正军,董冬冬,宋维琪,等.相带控制下协克里金方法孔隙度预测[J].地球物理学进展,2012,27(4):1581-1587. [12] 张锐,王瑞和,王建冬.应用序贯高斯模拟法预测储集层潜在伤害[J].大庆石油学院学报,2009,33(2):58-62. [13] 瞿明凯.几种地统计学方法在县域土壤空间信息处理上的应用与研究[D].武汉:华中农业大学,2012.2.2 序贯高斯模拟与克里格法的关联
3 工程应用
3.1 技术路线图

3.2 初步储量估算模型
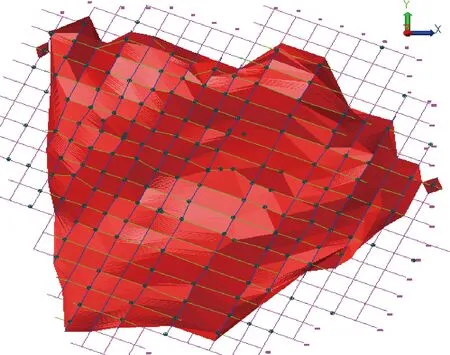

3.3 基于序贯高斯模拟的分层更新
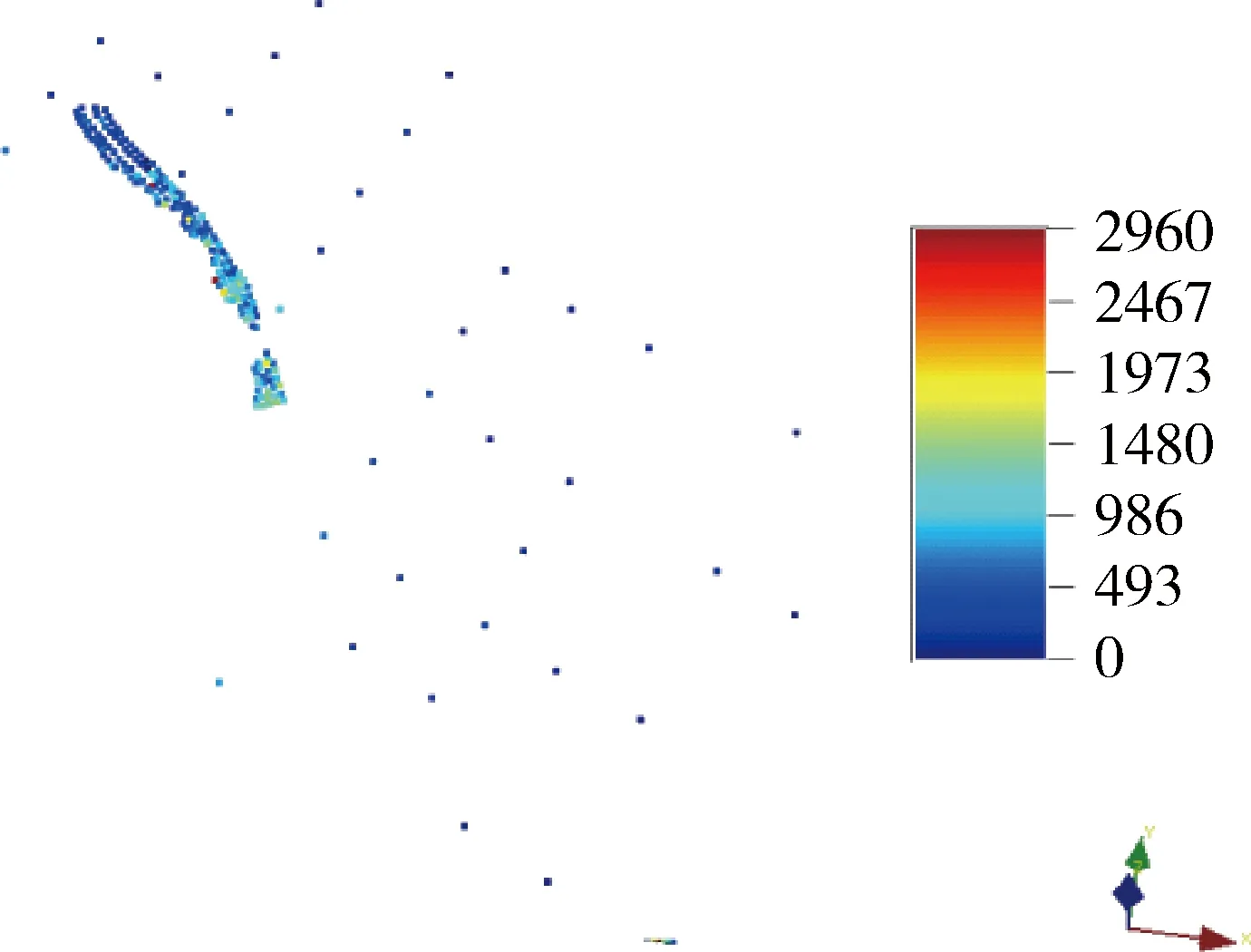
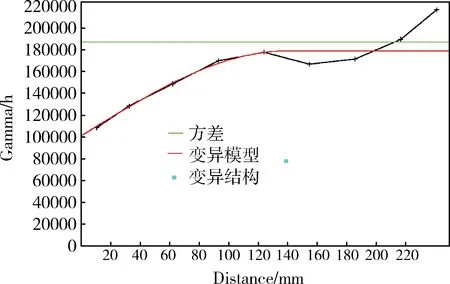

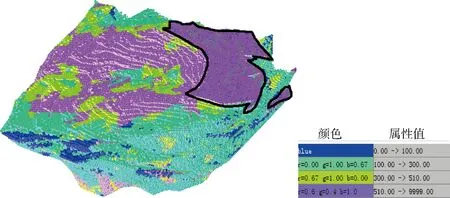
3.4 结果分析

4 结论

