基于双DSP 在交流位置伺服系统的小波神经网络控制

孔建平，高强，侯远龙

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

某海上火箭炮武器系统由于海洋环境扰动的作用、摩擦阻力和转动惯量、射击时较大的扰动力矩(强冲击)、机械传动的误差(如齿轮间隙)和机械传动系统的弹性变形，使得该伺服系统是一典型的非线性时变系统。采用常规的PID 控制器将无法得到响应快、控制精度高的交流位置伺服系统。小波神经网络为交流位置伺服系统控制开辟了一条新途径。而有关小波神经网络的研究目前大都处于仿真研究阶段，主要原因是小波神经网络控制器运算复杂、计算量大，一般的CPU 难以满足实时计算要求［1］。本文采用DSP 作为控制与运算单元，提出了一种针对不确定、不确知的系统和环境的在线实时控制系统，成功地实现了交流位置伺服系统的控制，且保证了系统的动、静态品质。

1 系统描述

某炮控交流伺服系统，其控制系统结构图如图1所示。

图1 炮控交流伺服系统结构图

2 小波神经网络控制器设计

小波神经网络控制系统结构图如图2 所示。

图2 小波神经网络控制系统结构图

采用双DSP 作为海上火箭炮武器系统的控制模块，其中DSP_1 作为小波神经网络的控制器，另一片DSP_2作为对象(此非线性交流伺服系统)的BP 神经网络辨识器。r 为目标位置量，y 为当前位置量，e 为r 与y 的差值，u 为控制电压，为辨识器辨识y 的辨识量。

双DSP 的硬件架构如图3 所示。

图3 中双口RAM 左边是控制部分，右边为辨识部分。控制计算机给出的目标角度值(r)经过CAN 通信给控制器DSP_1，r 与y 的差值e，经过小波神经网络算法计算出DA 值(u)，通过DA 模块输出。DA 值(u)再经过双口RAM 共享到DSP_2，当前位置量y 通过RDC 模块，经过I/O_2 输入给DSP_2。u 与y 作为辨识器DSP_2 的BP 网络的输入，输出为，与y 的差值e1，通过误差反传改善BP 神经网络的权值。下一时刻，控制计算机给出下一个目标角度值(r)，由于控制对象还未及时做出响应，得不到这一时刻的y，所以辨识器必须预测出这一时刻的，r与的差值e2，通过误差反传改善小波神经网络的权值和小波平移因子和伸缩因子。通过EEPROM_1 保存小波神经网络的权值和小波平移因子和伸缩因子，BP 神经网络的权值由EEPROM_2 保存。

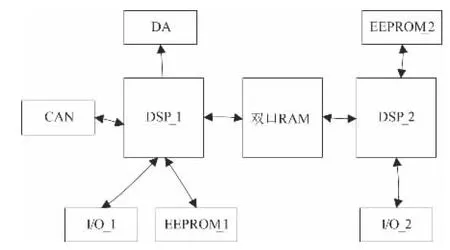
图3 双DSP 的硬件架构

3 小波神经网络

对∀Ψ∈L2(R)，如果Ψ(t)的傅里叶变换(w)满足如下可容许条件:

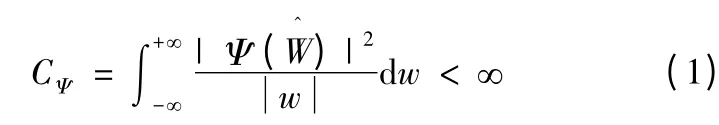
则称a，b∈R，a≠0 是一个基本小波(“基小波”)。

由小波母函数进行伸缩和平移生成的函数系{Ψa，b(t)}

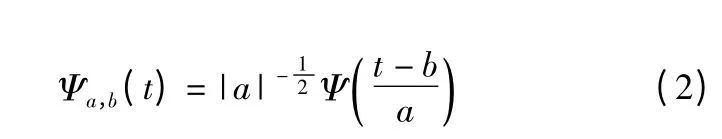
称为由小波母函数Ψ 生成的依赖于参数a 和b 的连续小波，其中，a 是尺度参数，b 是平移参数，且a，b∈R，a≠0，时间变量t、伸缩因子a 和位移因子b 都是连续变量。

目前小波神经网络的研究广泛采用将常规神经网络的隐层节点激励函数用小波函数代替，相应的输入层到隐层的权值及隐层阀值分别由小波函数的尺度参数和平移参数代替。连续性小波网络的结构如图4 所示。

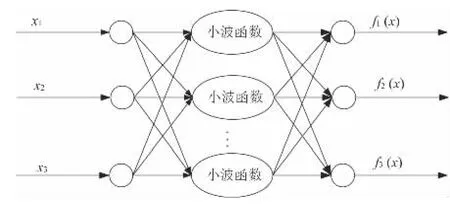
图4 连续性小波网络的结构图

小波神经网络参数的算法可以采用梯度下降法、正交搜索法等。实际上，由于小波神经网络的输出与其权值是线性的，不存在像常规BP 神经网络那样的局部极小缺陷，所以，可直接利用最小二乘法或数值鲁棒性更好的正交最小二乘法、UD 分解最小二乘法等方法辨识权系数［3］。

小波神经网络隐层节点个数的选择可借鉴以下经验公式［4］:

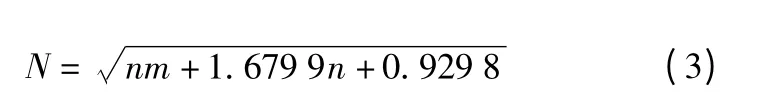
式中，N 为隐层节点数;n 为输入节点数;m 为输出节点数。

此系统中，n，m=1，N=1.899 9，四舍五入取N=2。另外，采用已经被用于各种领域的Morlet 小波(cos(1.75t)exp(－t2/2))作为神经网络的激励函数。

小波神经网络的权值初始化同BP 神经网络一样比较简单，但是小波函数的伸缩参数和平移参数aj和bj(j=1，2)的初始化稍微复杂一些。若小波神经网络初始化没做好，网络可能不会收敛。

为了初始化aj和bj，先要在输入域［c，d］当中找到一个点p，即c ＜p ＜d。为了选择点p，首先引进一个密度函数:

在计算密度函数中，可以粗略估计η(x)的大小，这样就可以把区间［c，d］的重心赋予p，即:

把p 点选择好以后，可以令a1=p，b1=ξ(d－c)

式中，ξ 取一个合适的正数常量(典型的可以取0.5)。这样，区间［c，d］就被点p 分为两个区间了。任取一个区间重复以上步骤，就可以初始化参数a2和b2了。

4 小波神经网络在DSP 上的实现

本文的DSP 芯片采用TI 公司的TMS320F28335，双口RAM 芯片采用CY7C057V，DA 芯片采用16 位DAC8544，双口RAM 和DA 芯片与DSP 的外部接口相连。主程序流程图如图5 所示。控制器系统通电初始化结束后进入CAN 接受中断。若产生CAN 中断响应进入主循环。然后进行读取I/O 操作、小波神经网络算法、DA 转换、双口RAM 写操作、CAN 接受中断、双口RAM 中断、双口RAM读操作、修改小波神经网络权值、小波平移因子和伸缩因子。辨识器系统通电初始化结束后进入主循环，然后进行双口RAM 中断、双口RAM 读操作、读取I/O 操作、BP 神经网络辨识、预测、修改神经网络权值、双口RAM 写操作。

5 实验结果

该型火箭炮伺服系统的水平方向技术指标如下:炮塔由0 mil 转至3 000 mil 的时间应小于6 s，稳态误差范围为－1.2 mil～1.2 mil。对于输入阶跃信号和正弦信号，系统的控制实验结果如下。

1)阶跃输入信号

3 000 mil 大范围调炮控制效果图如图6，图7，图8所示。

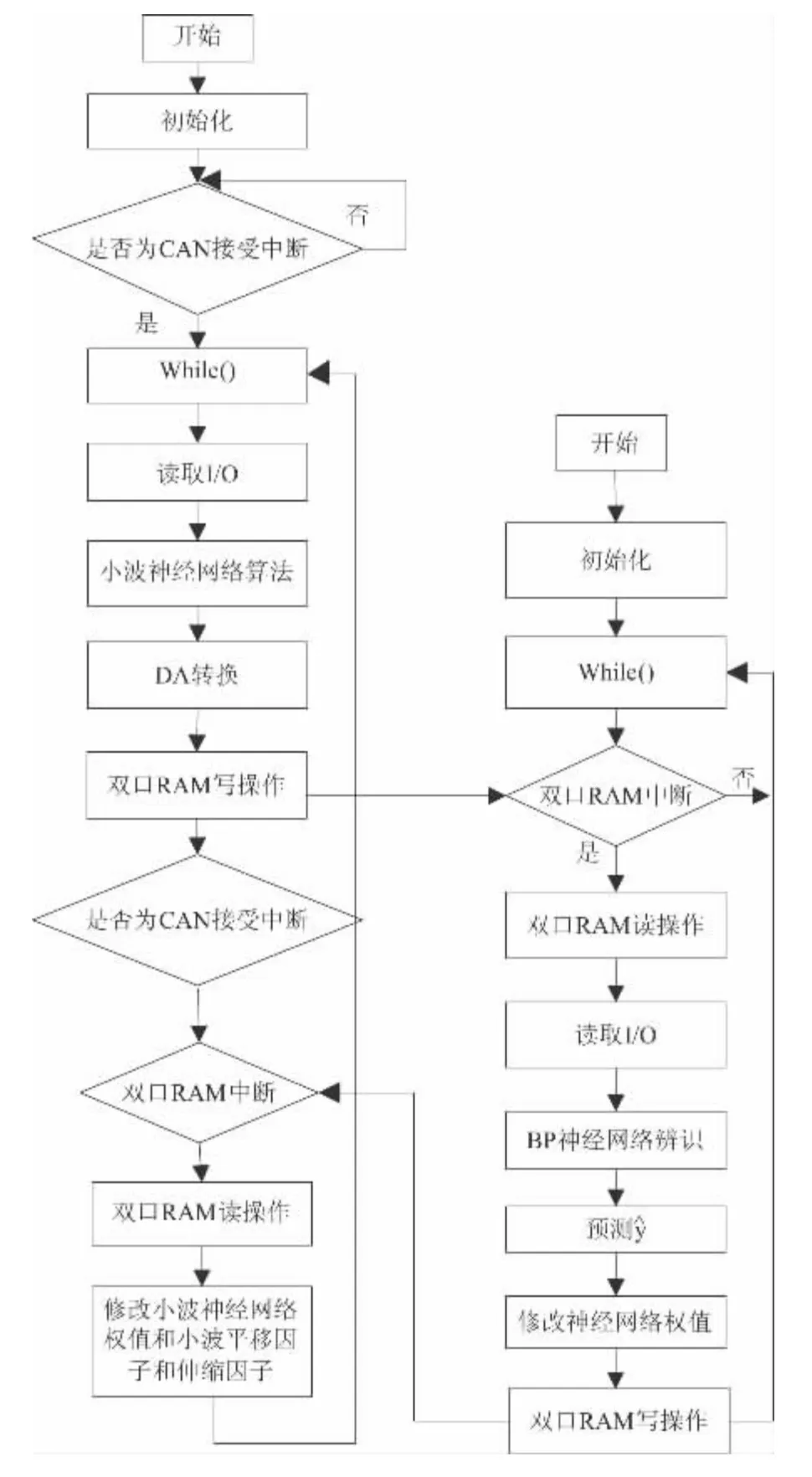
图5 主程序流程图

图6 调炮3 000 mil 系统跟踪响应曲线

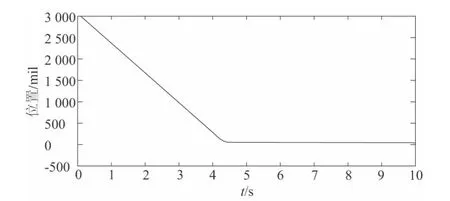
图7 调炮3 000 mil 系统跟踪响应误差曲线

图8 局部放大图

从图6，图7，图8 中可以看出，本文设计的控制器对该系统进行大范围调炮时，响应速度快，小于系统要求的6 s 技术指标，仅有一次1.2 mil 超调并能很快稳定，基本无振荡，对干扰信号抑制效果较好，且稳态误差小于±0.3 mil，完全能够满足系统的性能要求。

2)正弦输入

系统的正弦输入响应，主要检验系统的加速度特性。若输入信号的频率过快，则可能会因系统本身的响应较慢而无法跟踪目标位置，造成控制效果的失真。故本文采用的正弦输入信号为r(t)=20sin(0.4π × t)，其幅值为20 mil，周期为5 s。控制效果如图9，图10 所示。

图9 正弦输入的系统响应跟踪曲线

图10 跟踪误差曲线

从图9 和图10 看出系统具有很好的加速度特性，对干扰信号有较好的抑制，能够很好的跟踪正弦输入，且误差一直保持在±0.3 mil 之间，完全能够满足系统的精度要求。

6 结语

本文所设计的双DSP 系统很好地实现了小波神经网络控制器和BP 辨识器数据共享与协同处理，小波神经网络有较强的函数学习能力和逼近能力。实验结果表明，设计系统的响应速度快，基本无超调，最终的稳态误差都能保持在±0.3 mil 之间，且跟踪速度快，无滞后现象，有着很好的加速度性能。该双DSP 控制器完全能够满足此类型炮控系统的要求。但是由于神经网络是并行结构，而且DSP 的多种中断难以保证两片DSP 的数据共享与高度的同步性。故高度并行的FPGA 将是将来神经网络研究重点。

［1］高建臣，陈之龙，吴平东.DSP 在模糊神经网络控制器中的应用［J］.北京理工大学学报，1996，16(5):538-544.

［2］田雨波.混合神经网络技术［M］.北京:科学出版社，2009:298.

［3］田雨波.混合神经网络技术［M］.北京:科学出版社，2009:301.

［4］高大启.线性基本函数面向三层神经网络结构研究［J］.电路与系统学报，1997，2(3):31-37.