基于预测控制的变风量空调系统控制性能实验研究

，，

(中原工学院，郑州 450007)

变风量空调因具备灵活性高、节能性强等优点已成为国内外空调系统的主流[1].但是，由于变风量空调具有多变量、强耦合、非线性、时变性等特点，其设计、运行和管理都比定风量空调系统难度大[2-4].传统变风量空调的多回路PID控制系统在风量调节过程中，存在各支路管网相互影响、调节时间长、稳定性差等缺点[5].本文基于变风量空调送风系统运行机理，建立预测控制模型，对各送风支管的结构进行预测，提高了系统的稳定性；在预测控制的基础上增加PID反馈调节，提高了控制系统的精度，增加了控制系统的可靠性.

1 预测模型的建立

本实验台的建筑原型为郑州市某办公楼第二层的3间办公室，该建筑的结构及功能如图1所示.

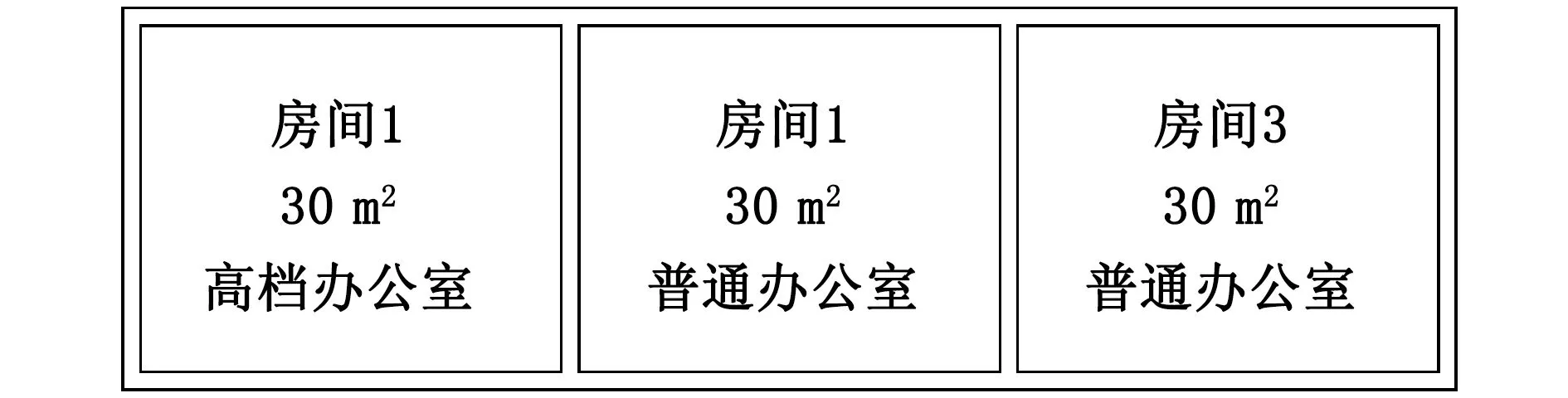
图1 建筑物结构功能图

将以上3间办公室等比例缩小，得到实验台3个空调小室，以3个空调小室为对象设计变风量空调系统实验台.该实验台送风系统如图2所示.为了便于建立预测控制模型，将其进一步简化，如图3所示.

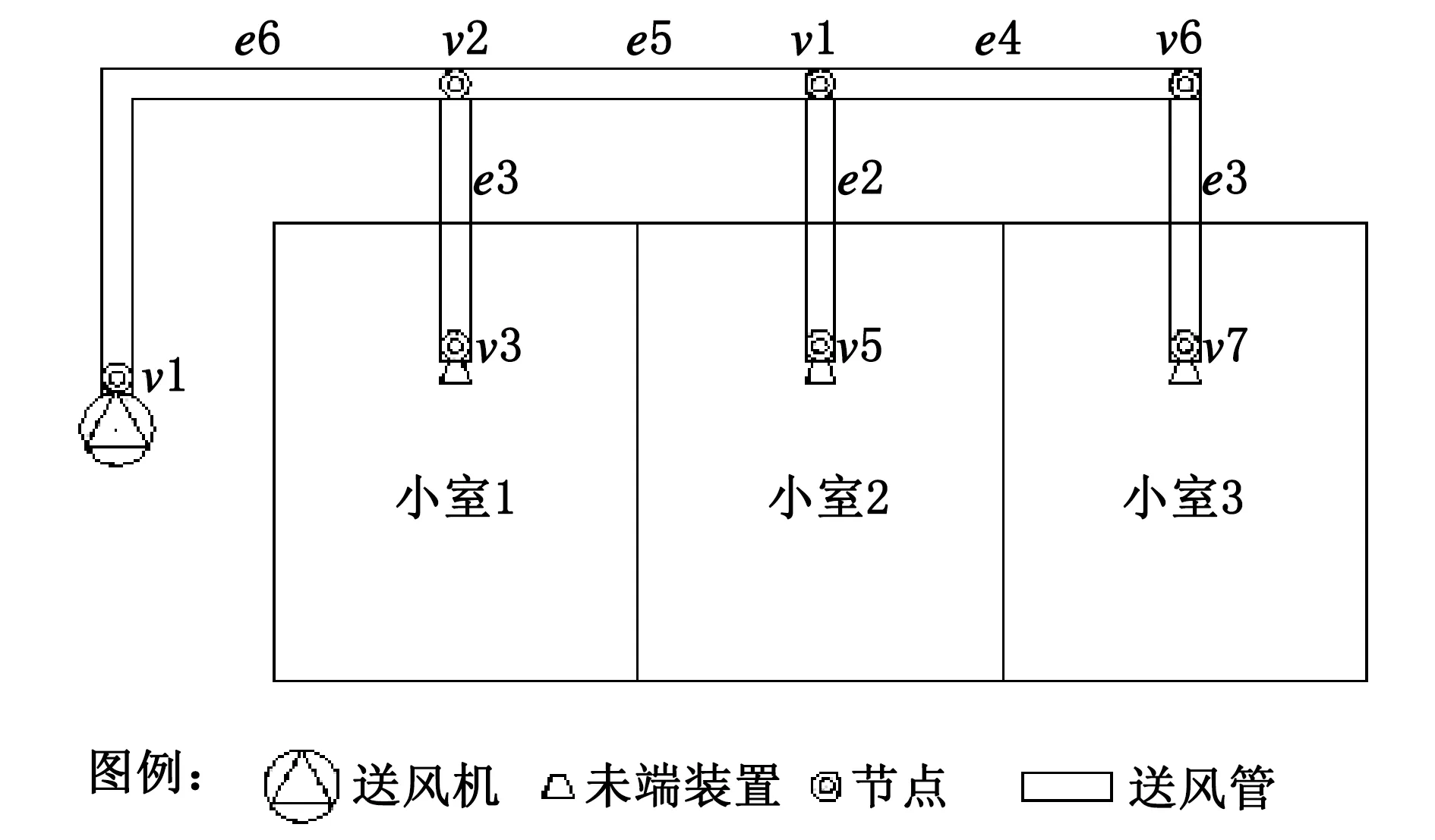
图2 实验台送风系统图

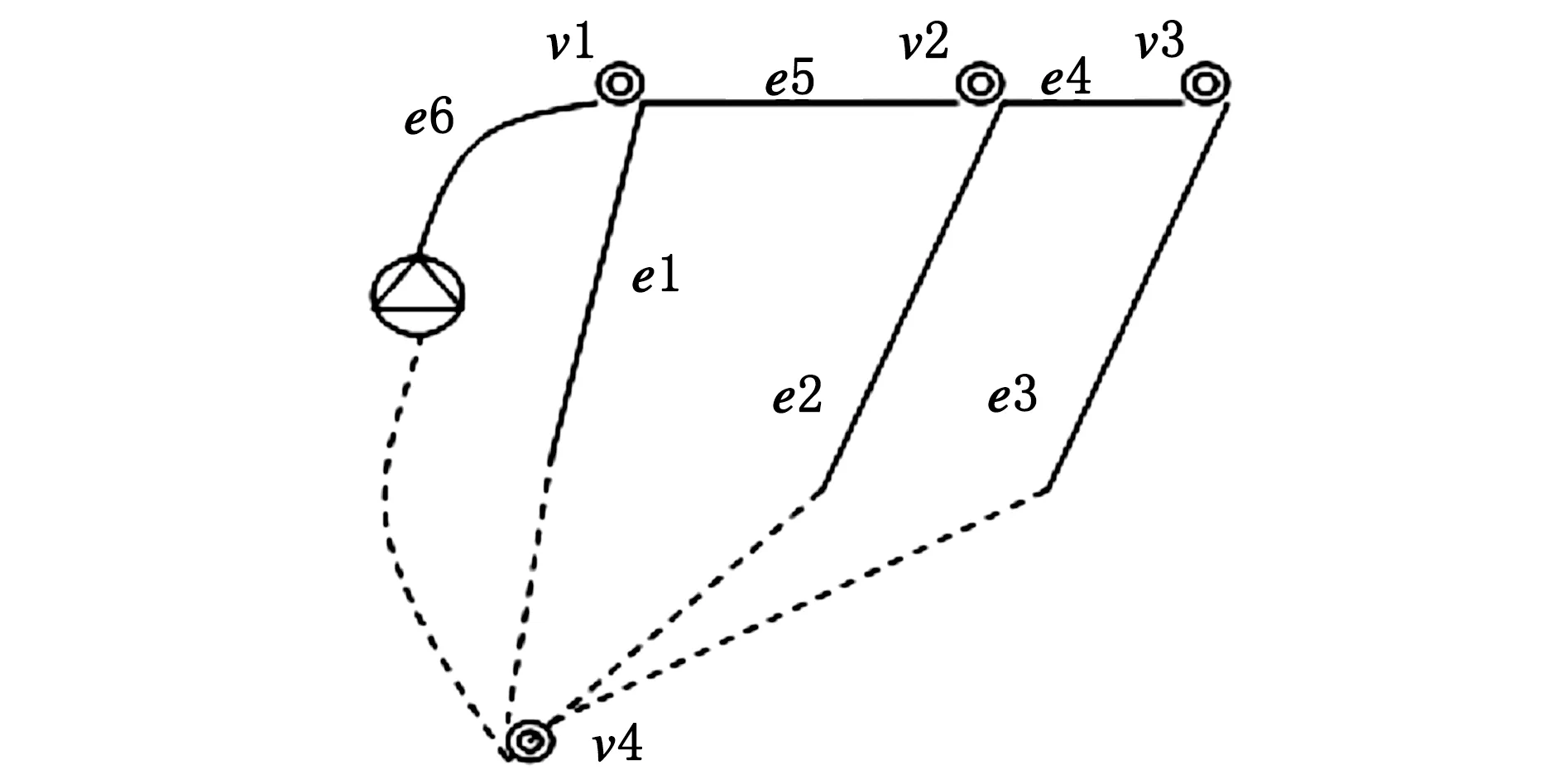
图3 实验台送风系统简化图

由流体力学理论可知，空调送风系统各支管管网阻力特性方程为[4]：

(1)

式中：ΔPi——风管进出口压差；

Si——风管的阻抗；

Qi——风管的风量.

由上式可知，管网的阻抗值与风管进出口压差成正比，与流量的二次方成反比.因此，当风管进出口压差已知时，即可根据各空调小室的需求风量预测出各送风支管的阻抗值.本实验风机采用定静压控制方式，定压点取在管段e4节点v2后侧，系统送风静压为570 Pa.本实验台送风主管较短且未设置调节装置，因此可以认为节点v1、v2、v3处压力均为570 Pa.各空调小室内静压满足暖通空调对室内静压的要求，维持5～10 Pa正压，各小室通过缝隙与大气相通，由此可知各末端出口处压力相等.综上，各送风支管进出口压差为已知，其值为575 Pa.因此可根据各空调小室的需风量由公式(1)对送风系统管网结构进行预测.

2 基于前馈控制的变风量空调控制系统设计

2.1 实验台控制系统原理

本实验台控制系统的主要任务是完成多区域变风量空调系统风量的匹配，即当各空调区域负荷值发生变化时，控制系统通过检测信号、控制计算、输出控制信号完成对各空调区域风量的控制，使之与设定值相符.为了完成上述控制功能，结合预测控制模块，对本实验台控制系统进行综合设计.本实验台控制系统为前馈反馈综合控制系统，其原理图如图4所示.

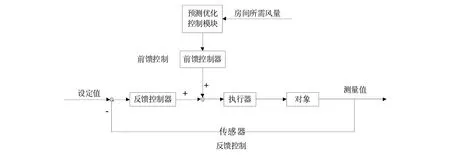
图4 控制系统原理图

各空调小室所需的风量为已知，预测控制模块根据各小室需求风量对变风量空调送风系统结构进行预测，前馈控制器根据预测结果调整末端风阀，以调节送入各空调小室的风量.在本实验系统中，预测优化控制模块虽然经过严密的理论推导，但在系统实际运行过程中，可能预测补偿会存在偏差而影响系统的控制品质，因此在本实验台控制系统加入反馈控制，这种前馈反馈综合控制系统，既解决了前馈控制偏差大的问题，又解决了反馈控制系统的时滞问题，达到了缩短调整时间、提高控制精度的目的.

2.2 控制程序设计

为实现以上变风量空调控制系统的控制功能，在上位机(组态王)中编写控制程序，控制程序可分为前馈控制程序和反馈控制程序两部分.前馈控制程序流程图如图5所示.前馈控制程序利用预测控制模型，对送风系统管网结构进行预测，根据预测结果调整末端阀门开度，最终达到调整风量的目的.反馈控制采用的是增量型PID控制，其程序流程图如图6所示.反馈控制根据风量设定值与反馈值的偏差，计算出输出增量后将计算结果赋给风阀执行器，风阀执行器产生动作，最终达到纠正风量偏差的目的.

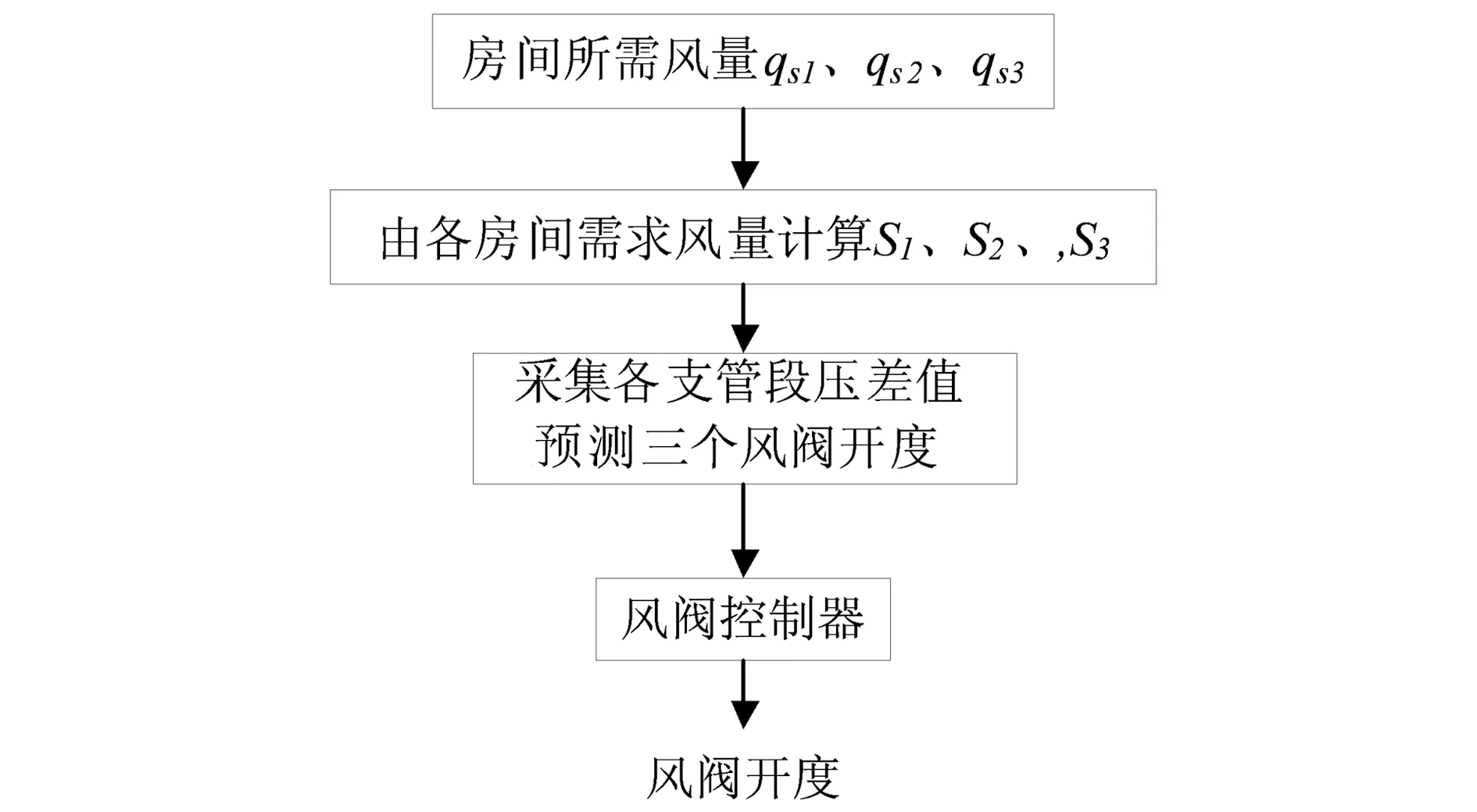
图5 前馈控制程序流程图

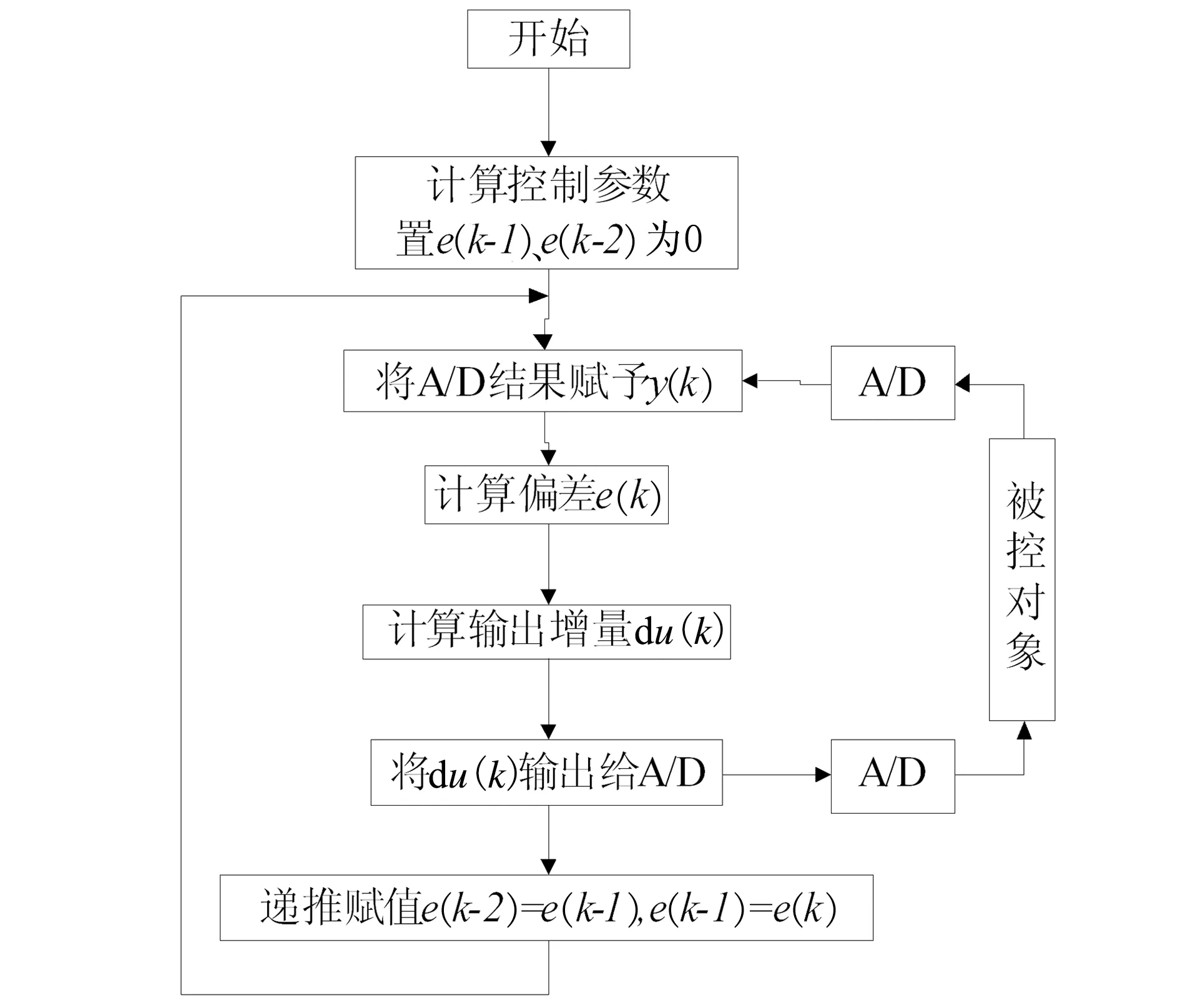
图6 反馈控制程序流程图

3 实验结果与分析

评判控制系统优劣的一个标准是系统受到扰动时，能否在控制器的作用下准确平稳快速地克服扰动造成的偏差.阶跃干扰对被控变量影响最大，控制系统如果能有效地克服阶跃干扰，那么也能很好地克服其他比较缓和的干扰.为评判控制系统优劣，设计一阶跃响应实验，将实验结果与相同工况的PID控制系统中的结果进行分析对比.

阶跃响应实验测试方案为：维持空调小室2、空调小室3的风量设定值75 m3/h和60 m3/h不变，在某一时刻将空调小室1的风量设定值从50 m3/h阶跃到100 m3/h.

图7为两种控制系统中的空调小室1的风量调节过程.两种控制系统中，小室1的风量调节过程都是非周期衰减过程，风量在设定值以下变化，没有来回波动，最后稳定在一个数值上.从两组实验结果可知，风量设定值发生阶跃变化后，两个控制系统在控制器作用下都达到新的稳定状态，预测控制系统的稳态偏差相对较小，预测控制系统中风量调节时间短，仅为42 s，PID控制系统调中风量节时间为75 s；风量设定值较低时，控制系统稳态偏差较大，可达到10.9%.

图7 两种控制系统中小室1送风量调节过程

受空调小室1的风量阶跃变化影响，小室2的风量与设定值产生偏差，系统开始对小室的2风量进行调节.图8为两种控制系统中空调小室2的风量调节过程.从以上两组实验结果可知，预测控制系统比PID控制系统拥有更快的动态响应速度、更小的稳态误差.预测控制系统中风量调节时间为60 s，稳态偏差为0.56%；PID控制系统中风量调节时间为60 s，稳态偏差为1.7%.

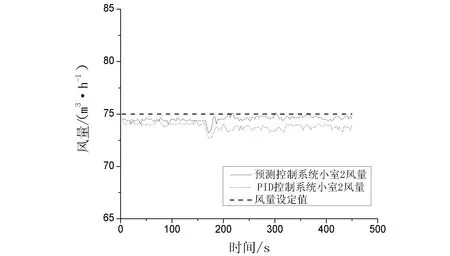
图8 预测控制系统中小室2送风量调节过程

图9为两种控制系统中空调小室3的风量调节过程.从图中可以看出，预测控制系统中空调小室3的风量基本未受小室1风量阶跃变化的影响，其风量一直在设定值附近波动，系统稳态偏差为0.23%；PID控制系统中，小室3的风量受小室1风量阶跃变化的影响较大，PID控制系统对小室3的风量进行调节，调节时间为87 s，系统稳态偏差为1.8%.

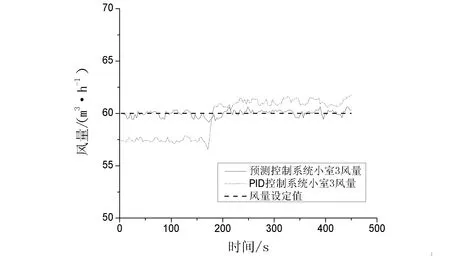
图9 两种控制系统中小室3送风量调节过程

图10为预测控制系统中末端风阀调节过程.从图10可看出，当小室1的风量发生阶跃变化后，在预测模型的作用下，阀门开度直接调整到38.94%，后又经预测控制系统中的PID控制反馈调节，最终稳定在41.14%，调节时间为39 s.图11为PID控制器系统中末端风阀调节过程.从图11可以看出，PID控制系统中阀门调节时间需要60 s，在调节过程中房间风量阶跃变化的风阀出现较大的波动，阀门开度大范围的波动将导致送风系统结构的剧烈变化，进而影响送风系统的风量分配，不利于系统的稳定运行.以上实验结果说明，预测模型对变风量空调送风系统的结构预测是准确的，避免了末端风阀的大幅度调节，提高了控制系统的稳定性.

图10 预测控制系统中末端风阀调节过程

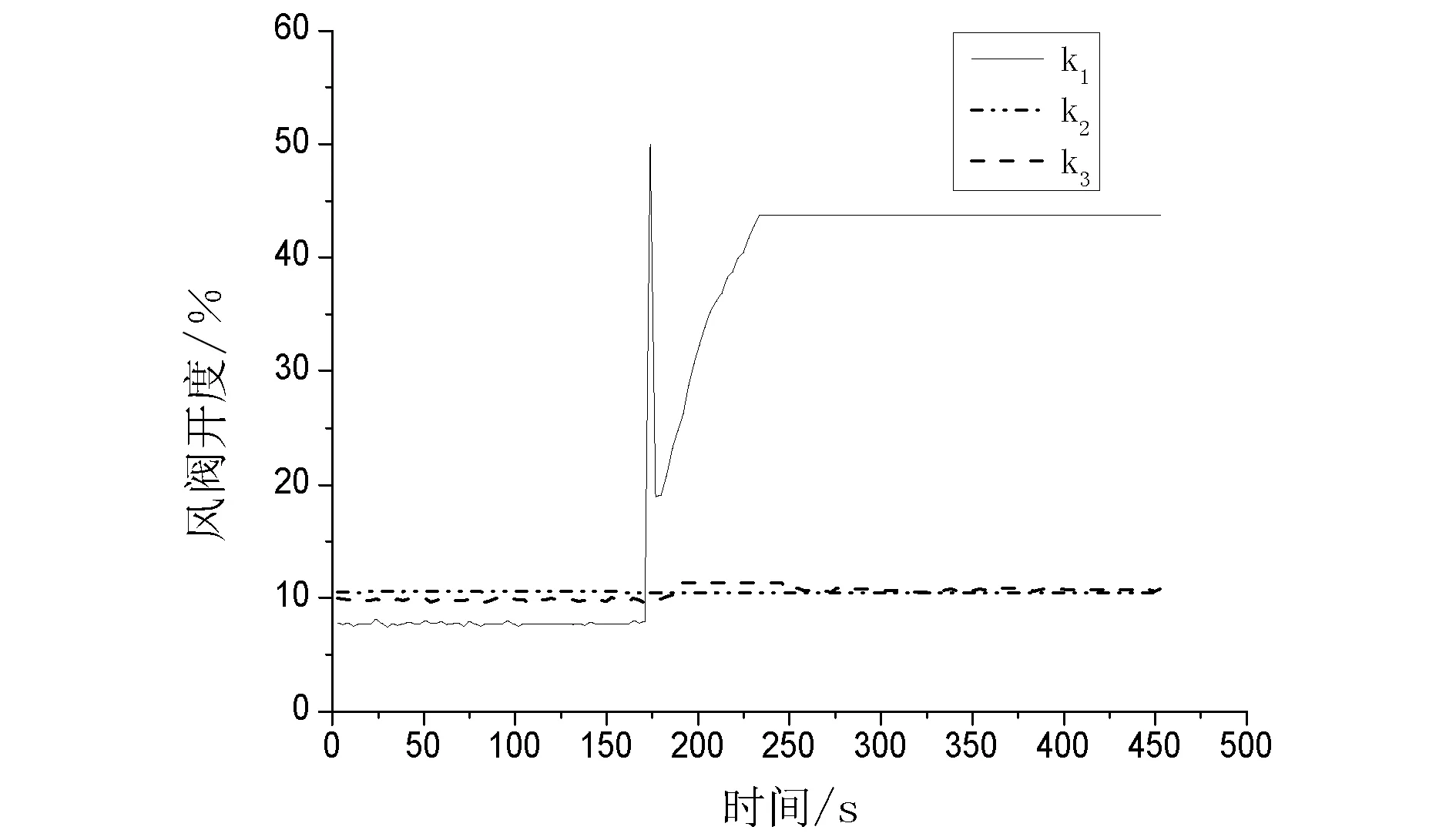
图11 PID控制器系统中末端风阀调节过程

以上两组控制系统的阶跃响应实验对比结果表明，基于预测控制的变风量空调控制系统，预测控制模块对变风量空调送风系统的结构预测准确，各个末端控制环节耦合小，其中距阶跃响应小室较远的小室的风量几乎未到影响；预测模块作用结束后，各末端风阀均在较小范围内进行调节，提高了系统的稳定性.可见，基于预测控制的变风量空调控制系统对风量的控制达到了及时、准确、稳定的要求.

4 结 语

本文研究了基于预测控制的变风量空调系统的控制性能，得到以下结论：

(1)预测控制模块对变风量空调送风系统的结构预测准确，预测模块作用下各控制环节耦合小，各控制环节能够相对独立调节，控制结果准确，稳态误差小，调节迅速，预测控制系统可快速、稳定、可靠地运行.

(2)基于预测控制的变风量空调控制系统与常规PID控制系统相比，控制精度更高，调节时间更短.将该控制系统应用于变风量空调系统，可以大大地改善其稳态性能和动态性能.

参考文献:

[1] 陈向阳. 变风量空调系统的自动控制[J]. 暖通空调, 1997,27(3):34-39.

[2] 田应丽，任庆昌. 基于DDC的变风量空调机组复合模糊控制[J]. 制冷与空调，2007,7(6):17-21.

[3] Darrell D, Massie. Prediciting Control Plant HVAC Equipment Performance Using Neural Net-works-laboratory System Results [J]. ASHRAE Trans, 1998,104(1):221-228.

[4] Erik J. Experimental Results of a Predictive Neural Network HAVC Controller [J]. ASHRAR Trans, 1998, 104(2):404-408.

[5] 孙宁，李吉生，彦启森. 变风量系统耦合特性研究第二部分：应用分析[C]//全国暖通空调制冷1998年学术文集.北京：中国建筑工业出版社，1998：392-395.