具有随机时滞和丢包的非线性网络控制系统的H∞滤波器设计

赵立英，窦立亚

(北京科技大学 数理学院，北京，100083)

滤波已经成为控制和信号处理过程的关键问题。对于一个给定的带有测量误差的系统，滤波用来估计无法测得的状态变量[1-2]。滤波系统通过网络传输信号被称为基于网络的滤波系统。基于网络的系统有很多优点，例如成本低，易于安装维护，可实现远程操作和控制，灵活性高等，受到了广泛的关注[3-4]。然而，传输网络通常是不可靠的，会出现数据包丢失和网络诱导时滞等现象，这将明显降低系统的性能，所以，需研究更准确地建模以及进行量化估计[5-8]。近年来，基于网络系统的滤波问题已取得一些研究成果，大部分成果是通过Kalman 滤波方法得到的。Kalman 滤波方法是目前处理状态估计问题应用最广泛、有效的方法，但它要求系统模型是精确的，并且外部噪声的统计信息准确已知，这些假设在实际应用中不易达到。H∞滤波不要求精确的外部扰动信息，并能保证一定的噪声衰减率及对噪声的鲁棒性，对网络控制系统的H∞滤波问题的研究逐渐出现[9-17]。对带有时滞、丢包和模型不确定性的连续网络控制系统，Yang 等[5]给出了其H∞滤波器设计过程。Yue 等[10]研究了带有多重随机丢包的离散网络控制系统的H∞滤波问题，滤波误差系统被描述成一个离散的马尔可夫系统。本文作者研究的网络控制系统是带有非线性项的离散非线性网络控制系统。在网络控制系统中，由于信号在网络中传输可能发生数据拥堵现象，网络诱导时滞可能是变化的，考虑的网络诱导时滞取值于一个有限的集合dk∈{τ1,τ2, …,τq}，每个时滞τi，i=1，2，…，q 的发生概率已知，也考虑了丢包以及分布时滞对系统的影响[5]，并对滤波误差系统进行建模，构造Lyapunov 泛函，设计出使系统稳定的H∞滤波器。

1 问题描述

考虑以下带有混合随机时滞和丢包的离散非线性网络系统：

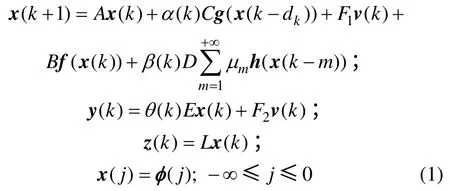
式中： x( k )∈Rn为状态向量， y( k )∈Rr为系统输出，z( k )∈Rp为要估计的信号； v( k )∈Rs为外部扰动且属于 L2[0, ∞]；f ( x( k)) =[ f1( x( k)), …, fn( x( k ))]T，g ( x( k)) =[ g1( x( k)), …, gn( x( k ))]T,h( x( k)) =[ h1( x( k )),…, hn( x( k ))]T为非线性函数； 初始条件为φ( j),-∞≤ j≤ 0。

假设离散时滞dk取值于一个有限的集合，即dk∈{τ1,τ2, …,τq}，{dk}相互独立且分布情况相同，发生概率如下：

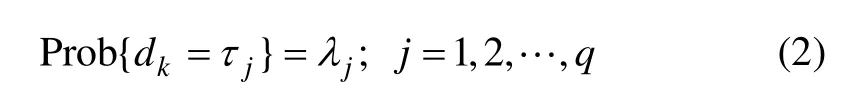
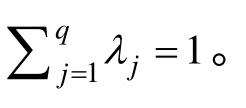
注1：网络控制系统由网络将传感器、控制器和执行器连接组成分散式闭环反馈控制系统，一般用于实现远程操作和控制。远距离网络传输有可能受到外部一些非线性因素的影响，所以，系统(1)中引入了非线性项 f ( x( k))， g ( x( k))和 h( x( k))。系统(1)的测量输出模型考虑了测量丢失的情况，当 θ( k) = 0，且实际信号被丢失时，此时系统输出只包含噪声，在实际应用中目标跟踪就是这种情况。

注2：很多已有研究离散时间时滞系统的文献都建立在以下假设下：

假设(2)与假设(3)有很大不同，并且具有有一些优点。假设dk在{1，3}中取值，若利用假设(3)，此时dm=1，dM=3，这就相当于假设dk也可以取值为dk=2，这就造成对系统的实际时滞描述不精确[3]。

常数μm≥0, m =1, 2,…，满足以下收敛条件：

式(1)中随机变量 α( k)， β( k)， θ( k)是相互独立的，并符合Bernoulli 分布的序列，满足以下分布规则：

由于网络的复杂性，在实际测量时会有一些外部噪声，引入随机变量 α( k)， β( k)和 θ( k)用来建立离散时滞、分布时滞以及系统输出的概率模型。

根据系统输出y(k)估计z(k)，本文考虑的滤波器是线性的，形式如下：

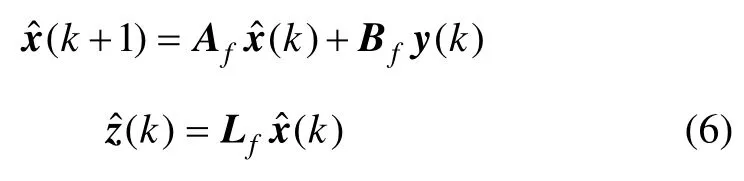
系统(1)可以写成

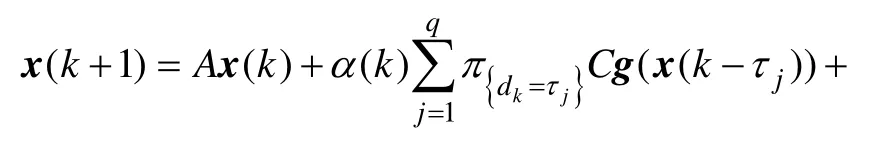
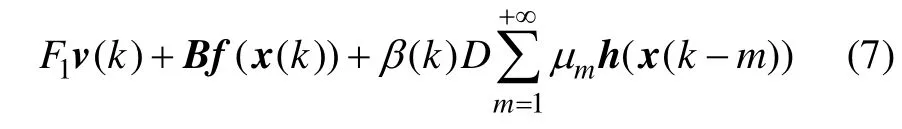
定义矩阵

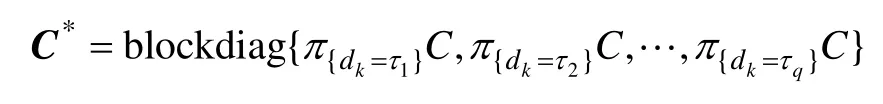
则式(7)可以变换为如下形式：

其中：

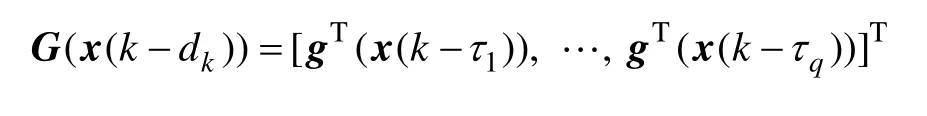
可以得到滤波误差系统：

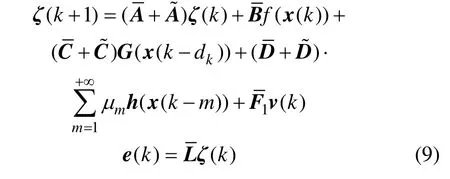
注4：本文考虑的离散时滞取值于一个有限的集合，并对应于一定的发生概率，相比文献[5]，描述实际系统更精确。对系统变换时出现 G ( x(k -dk))，相比于文献[5]包含更多的信息。

定义1：当v(k)=0 时，滤波误差系统(9)是均方渐近稳定的，对于任意初始条件，下式成立：

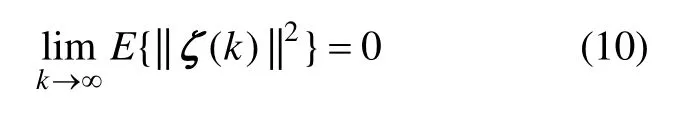
定义2：给定标量γ＞0，滤波误差系统(9)是均方渐近稳定的，满足H∞性能γ，在零初始条件下，对于一切非零的v( k )∈L2[0, ∞)，它是渐近稳定的，并且滤波误差e(k)满足

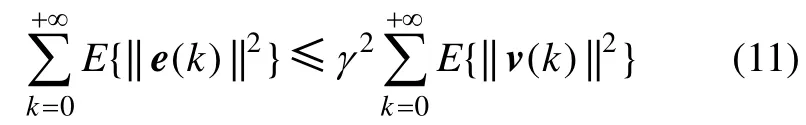
引理1[5]：设M∈Rn×n是半正定矩阵，xi∈Rn，ai≥0(i=1，2，…)。若相关序列是收敛的，则以下不等式成立：

为得到主要结果，对非线性函数f(·)，g(·)和h(·)进行以下假设。

假设1：f(·)，g(·)和h(·)向量有界，且

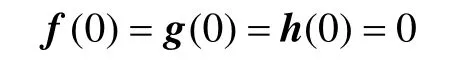
假设2：非线性向量赋值函数f，g 和h 是连续的，且对于 ∀x ,y ∈Rn，有

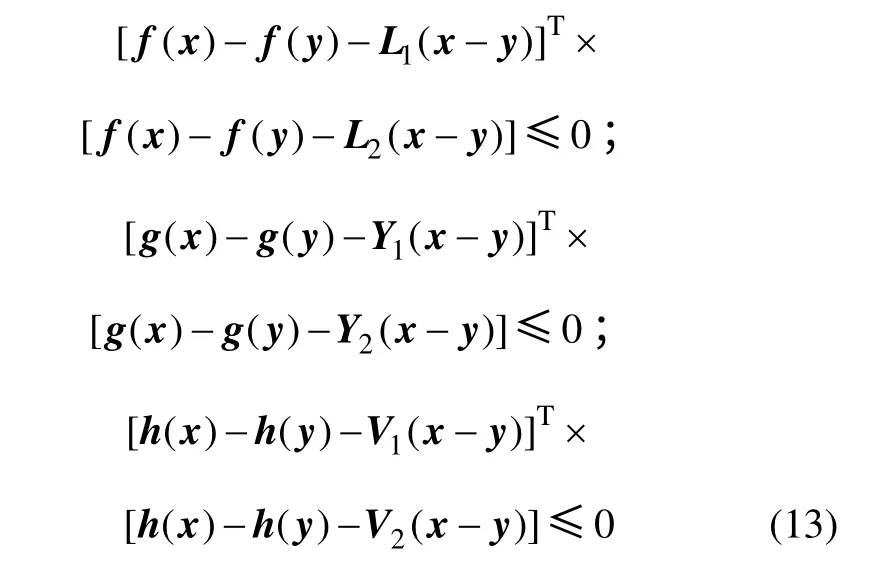
式中：L1，L2，Y1，Y2，V1和V2为常矩阵。

2 H∞滤波性能分析

在这部分，首先分析当v(k)=0时系统(9)的稳定性。

定理1：对于离散网络控制系统(1)，假定式(6)中Af，Bf和Lf是已知的，则当v(k)=0 时，滤波误差系统(9)是均方渐近稳定的，如果存在正定矩阵P，Qj和Zj，(j=1，2，…，q)，使得：

证明：构造Lyapunov 泛函如下：

当v(k)=0 时，沿着系统(9)的解求V(k)的导数并取其数学期望，得到

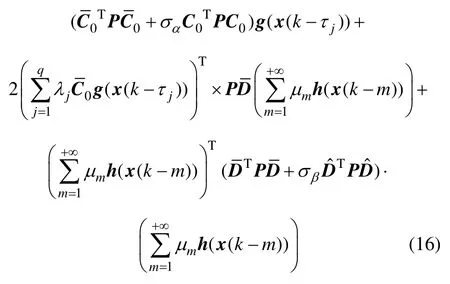
式(16)可以写成：

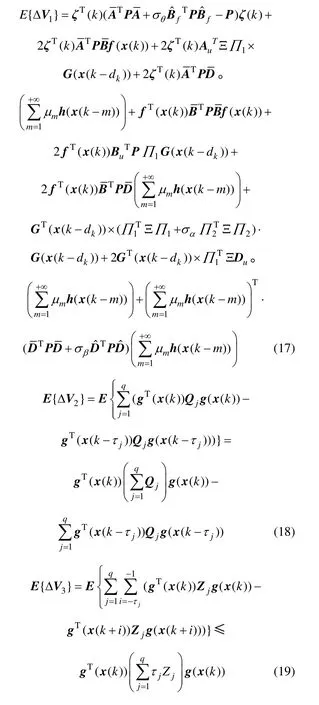
由假设1 和假设2 可直接得到

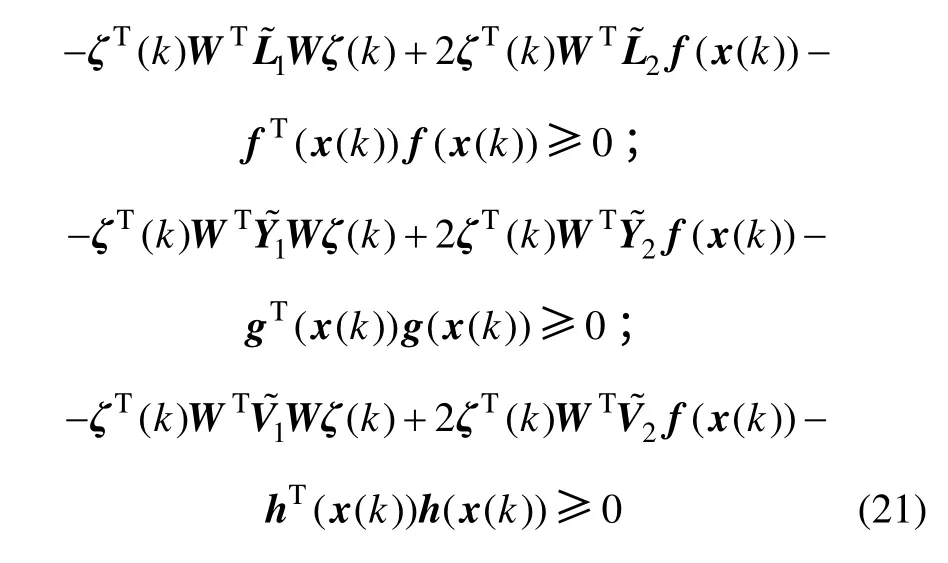
式中：

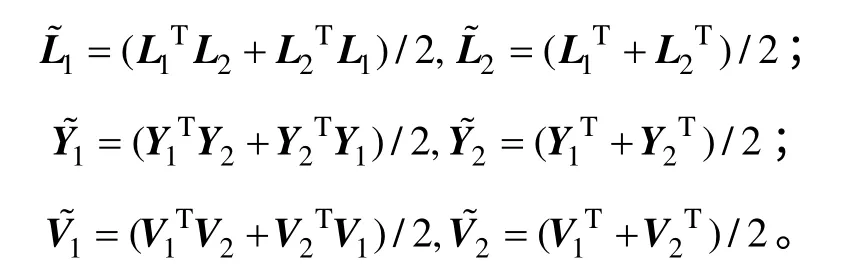
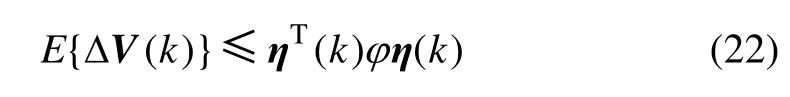
由式(14)和(22)得

根据Lyapunov 稳定性定理，对给定的滤波器参数，系统(9)是均方渐近稳定的。

下面对系统(9)进行H∞性能分析。

定理2 给定参数Af，Bf和Lf，设γ 是一个正常数，且当v(k)=0时滤波误差系统(9)是均方渐近稳定的，则在零初始条件下，对于任意非零的v( k )∈L2[0, ∞)，滤波误差e(k)满足式(11)，如果存在正定矩阵P，Qj，Zj(j=1，2，…，q)，R，使得：

证明 易证明当Φ＜0时φ＜0，由定理1 得，当v(k)=0 时滤波误差系统(9)是均方渐近稳定的。为研究其在零初始条件下的H∞性能，引入性能指标：

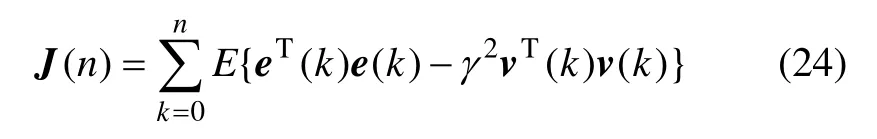
构造与定理1 相同的Lyapunov 泛函，进行类似的处理，可得

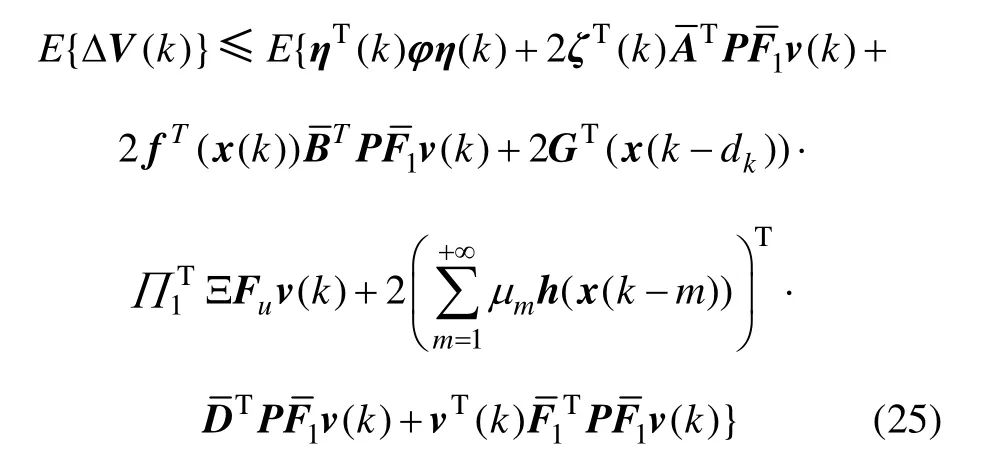
则由(24)和(25)可得

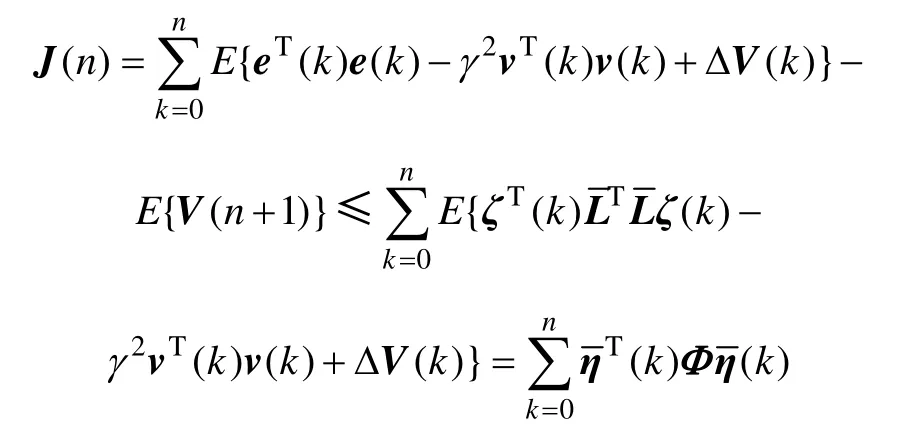
3 滤波器设计

为得到满足性能条件的滤波器，需要确定滤波器的参数Af，Bf和Lf，定理3 给出了滤波器的设计过程。

定理3 对于离散网络控制系统(1)，给定常数γ＞0，如果存在矩阵P＞0，R＞0，Qj＞0，Zj＞0，j=1，2，…，q，X 和Lf，满足：

其中：

则存在一个滤波器(6)使得滤波误差系统(9)在v(k)=0 时是均方渐近稳定的，且在零初始条件下，对于任意非零的v( k )∈L2[0, ∞)，滤波误差e(k)满足式(11)。

若以上条件有可行解，则满足条件的H∞滤波器的参数可由X 和Lf得到，

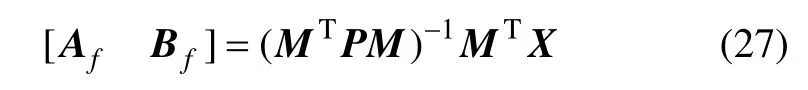
令

则式(23)等价于

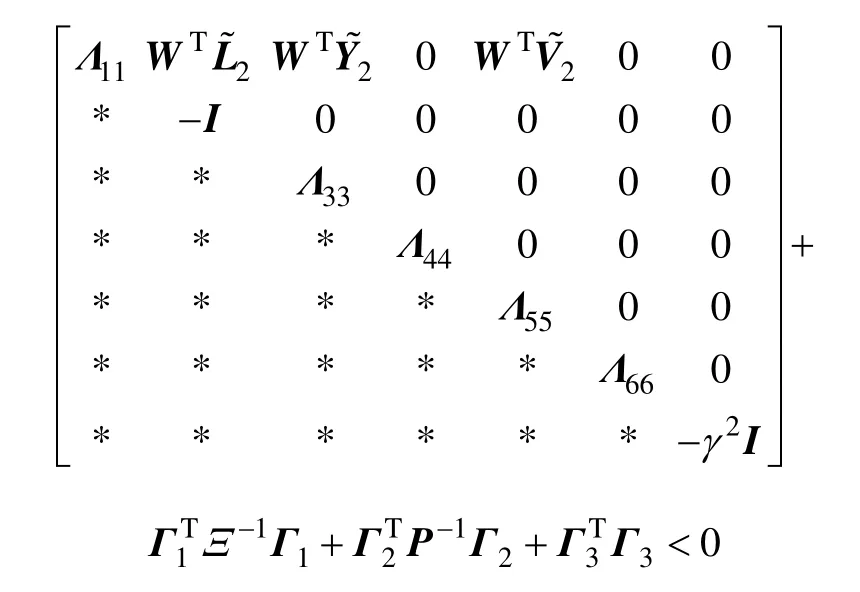
应用Schur 补定理，得

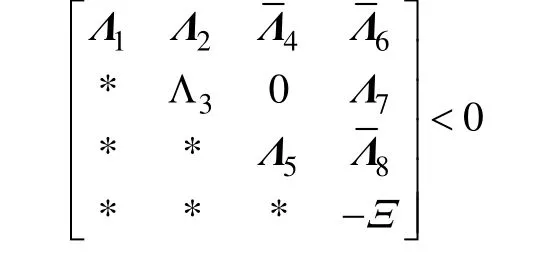
其中：

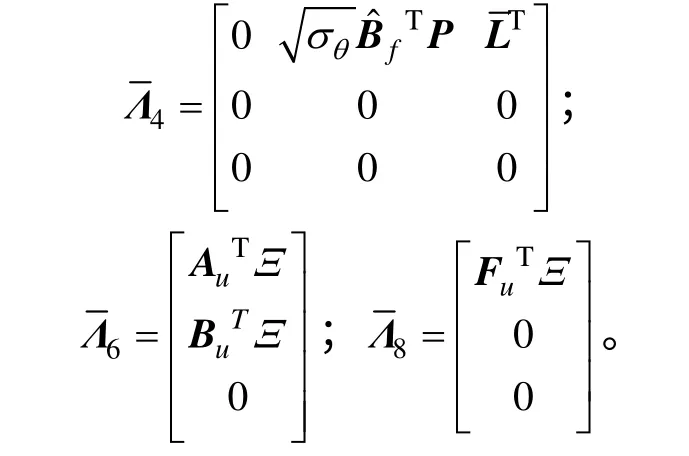
4 数值仿真

设系统(1)参数如下：

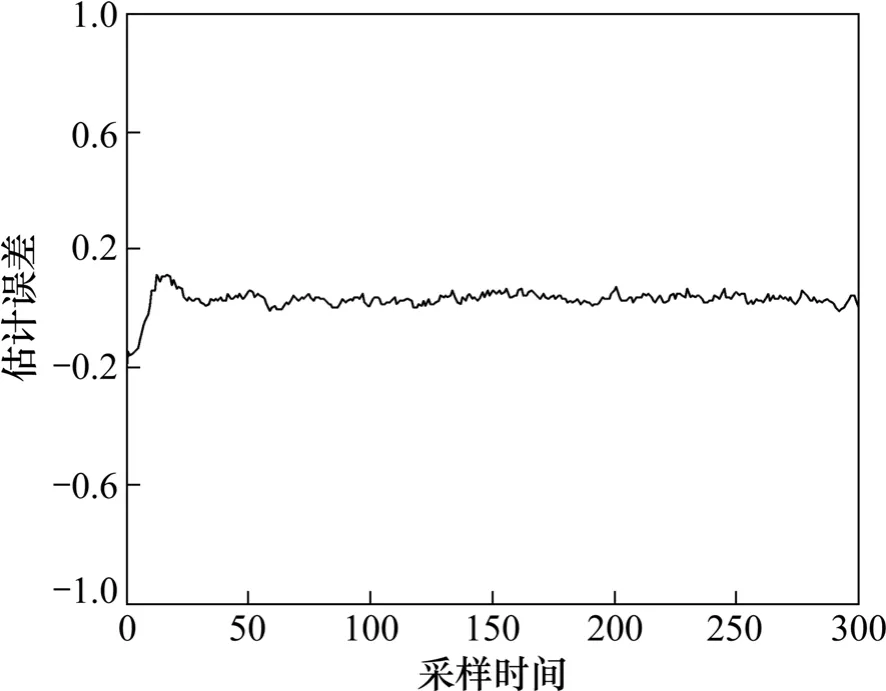
图1 当v(k)=0 时的估计误差Fig.1 Estimation error when v(k)=0

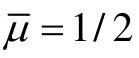
令γ=0.9，非线性向量赋值函数：

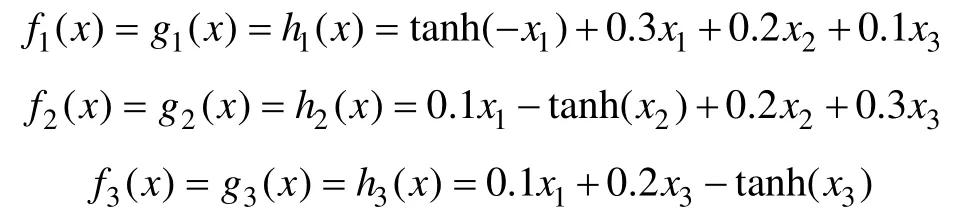
易验证

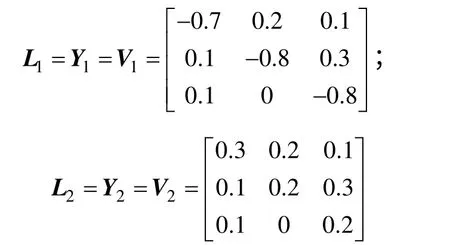
当v(k)=0 时，应用定理3，得到H∞滤波器的参数：

假设零初始条件下，外部扰动v(k)为

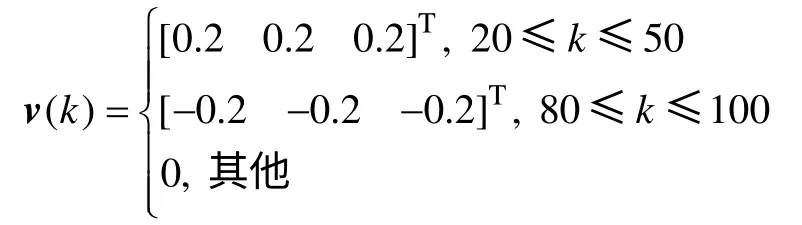
图2 显示此时的估计误差e(k)，网络诱导时滞dk在各采样时刻的取值如图3 所示，Bernouli 序列α(k)，β(k)和θ(k)如图4 所示。

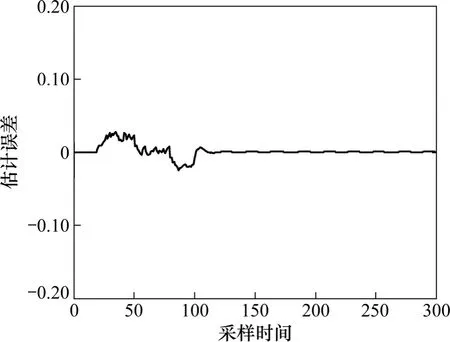
图2 估计误差Fig.2 Estimation error

图3 时滞dk 的分布Fig.3 Distribution of the time delay dk

5 结论

1) 解决了非线性网络控制系统的H∞滤波问题，网络诱导时滞在一种新的假设下，能更加准确、合理地描述时滞。

2) 应用Lyapunov 方法和线性矩阵不等式进行了H∞滤波性能分析，得到了使得系统均方渐近稳定的充分条件，并给出H∞滤波器设计步骤。数值仿真算例证明了本文提出算法的有效性。

[1] GAO Huijun, CHEN Tongwen. H∞estimation for uncertain systems with limited communication capacity[J]. IEEE Transactions on Automatic Control, 2007, 52(11): 2070-2080.

[2] Fridman E, Shaked U, Xie L. Robust H∞filtering of linear systems with time-varying delay[J]. IEEE Transactions on Automatic Control, 2003, 48(1): 159-165.

[3] GAO Huijun, MENG Xiangyu, CHEN Tongwen. Stabilization of networked control systems with a new delay characterization[J].IEEE Transactions on Automatic Control, 2008, 53(9):2142-2148.

[4] GAO Huijun, CHEN Tongwen, Lam J. A new delay system approach to network-based control[J]. Automatica, 2008, 44(1):39-52.

[5] YANG Rongni, SHI Peng, LIU Guoping. Filtering for discrete-time networked nonlinear systems with mixed random delays and packet dropouts[J]. IEEE Transactions on Automatic Control, 2011, 56(11): 2655-2660.

[6] Basin M, SHI Peng, Calderon-Alvarez D. Central suboptimal H∞filter design for linear time-varying systems with state and measurement delays[J]. International Journal of System Science,2010, 41(4): 411-421.

[7] Basin M, Gonzalez R R. Optimal control for linear systems with multiple time delays in control input[J]. IEEE Transactions on Automatic Control, 2006, 51(1): 91-97.

[8] 聂红伟, 马广程, 王常虹, 等. 一类通讯受限不确定网络控制系统鲁棒H∞滤波[J]. 控制与决策, 2008, 23(8): 888-893.NIE Hongwei, MA Guangcheng, WANG Changhong, et al.Robust H∞filtering for a class of uncertain networked control systems with limited communication[J]. Control and Decision,2008, 23(8): 888-893.

[9] PENG Chen, YANG Taicheng. Event-triggered communication and H∞control co-design for networked control systems[J].Automatica, 2013, 49(5): 1326-1332.

[10] YUE Dong, HAN Qinglong. Network-based robust H∞filtering for uncertain linear systems[J]. IEEE Transactions on Signal Process, 2006, 54(11): 4293-4301.

[11] ZHANG Wenan, YU Li. H∞filtering of networked discrete-time systems with random packet losses[J]. Information Sciences,2009, 179(22): 3944-3955.

[12] WANG Guoliang, ZHANG Qinglong, YANG Chunyu.Exponential H∞filtering for time-varying delay systems:Markovian approach[J]. Signal Processing, 2011, 91(8):1852-1862.

[13] LIU Ming, YOU Jia, MA Xincheng. H∞filtering for sampled-data stochastic systems with limited capacity channel[J].Signal Processing, 2011, 91(8): 1826-1837.

[14] SHEN Bo, WANG Zidong, SHU Huisheng, et al. Robust H∞finite-horizon filtering with randomly occurred nonlinearities and quantization effects[J]. Automatica, 2010, 46(11):1743-1751.

[15] YANG Hongjiu, XIA Yuanqing, SHI Peng. Stabilization of networked control systems with nonuniform random sampling periods[J]. Int J Robust Nonlin Control, 2011, 21(5): 501-526.

[16] JIANG Bin, MAO Zehui, SHI Peng. H∞filter design for a class of networked control systems via T-S fuzzy-model approach[J].IEEE Transactions on Fuzzy System, 2010, 18(1): 201-208.

[17] LIANG Yan, CHEN Tongwen, PAN Quan. Optimal linear state estimator with multiple packet dropouts[J]. IEEE Transactions on Automatic Control, 2010, 55(6): 1428-1433.