桩承式加筋路堤三角形布桩下桩土应力分析

刘洪凯，夏唐代

(1. 浙江大学 滨海和城市岩土工程研究中心，浙江 杭州，310058；2. 浙江大学 软弱土与环境土工教育部重点实验室，浙江 杭州，310058)

桩承式加筋路堤通过在软土地基中使用桩基从而达到加固深度较深、增加路基的稳定性和减小变形的目的，长期以来在高速公路和铁路工程中得到普遍采用。加筋路堤是由桩身与桩顶盖板、土工格栅、砂垫层联合形成的桩承式加筋复合地基。在刚性桩复合地基中，由于桩间土与桩之间的差异沉降，桩间土中将产生抵抗差异沉降趋势的剪应力，从而将路堤荷载传递给桩顶，这种荷载转移机理称为“土拱效应”。常规的桩承式路堤为了通过土拱效应将路堤荷载传递给桩，需要采用较小的桩间距或采用大尺寸的桩顶盖板，费用较大。若在桩顶布置一层土工合成材料加筋垫层，则可形成“拉膜效应”，大幅度增加桩的间距，降低工程造价。“土拱效应”和“拉膜效应”的产生将大大影响桩承式加筋路堤的桩体荷载分担情况，因此，研究复合地基受荷性状的这2 种作用效应至关重要。对于“土拱效应”的研究，Tergazhi[1]提出了平面土拱效应、Carlsson[2]提出了三角形拱、Low 等[3]提出了半圆形拱理论及Hewlett 和Randolph[4]提出了半球形模型。国内学者陈云敏等[5-6]结合现场试验分析，改进了Hewlett 的空间土拱极限分析方法，研究了桩帽大小、桩间距和填料内摩擦角对桩体荷载分担情况的影响；吕伟华等[7]假设理想条件下的倾斜滑移面，推导出在土工格栅不同挠曲变形时土体中剪应力的计算公式；蔡德钩等[8]通过模型试验研究了桩承路基结构中土拱效应及网垫的受力性状；强小俊等[9]对Hewlett 土拱效应所考虑的影响因素加以补充，得到了桩承式路堤土拱效应的改进算法；费康等[10]通过模型试验和有限元分析，研究桩承式路堤中填土的破坏模式；陈福全等[11]对矩形布桩情况下Hewlett 算法进行了改进，提出了桩体荷载分担比的计算公式。对于“拉膜效应”的研究，Kempfert 等[12]直接采用了弹性嵌固膜理论来计算土工合成材料中的拉力和应变，其计算出的拉力结果偏大；Giroud 等[13]则认为土工合成材料在桩边固定，变形后土工合成材料在平面内呈圆弧状；陈娟等[14]也通假设加筋垫层的弯沉呈抛物线形式对加筋垫层的受力分析进行理论推导，得到了桩网复合地基中拉膜效应产生桩间土应力变化情况。本文作者从三角形布桩情况下土拱和拉膜的形成情况出发，提出了等效桩帽的概念，将方形桩帽等效为六边形。假设土拱是由3 根等距离桩内接形成的半球环，分析边界条件与Hewleet 的假定有所不同，并在此基础上改进了传统的Hewleet 极限状态空间土拱效应分析方法，得到了土拱效应下桩土应力情况。假设拉膜区域同样由3 根等距离桩内接形成，加筋垫层产生的弯沉沿径向呈抛物线状，“拉膜效应”的产生进一步减小桩间土体应力情况，增加桩顶荷载分担。最终考虑两者共同作用情况下，得到了桩体荷载分担比的计算公式。本文提出的桩土应力分析方法同时考虑了桩网复合地基的“土拱效应”和“拉膜效应”，较以往单一的分析更具适用性，对于桩帽形状的合理假设使得计算分析具有可行性，为今后复杂布桩情况下的桩土应力分析提供了基础。

1 土拱分析

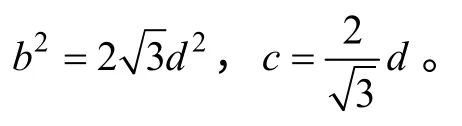
图1 三角形布桩下桩帽等效示意图Fig.1 Equivalent shape of piles cap in triangle

先分析土拱顶部的受力，取土拱顶部一单元土体进行受力分析，如图2 所示。其竖向平衡方程为：

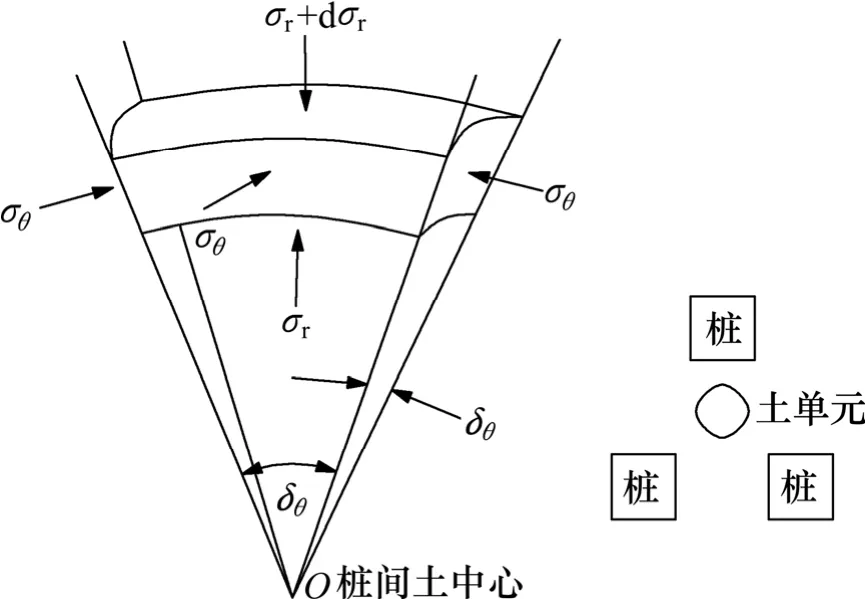
图2 土拱顶部单元体受力分析图Fig.2 Stress analysis of soil unit at the top of arch

式中：γ 为填土重度； σr为径向应力； σθ为环向应力；r 为土拱径向距离；α 为待定系数，1/Kp≤α ≤1。

以式(3)作为边界条件求解式(1)和(2)，得

顶部下拱面的压力 σit为

进一步可得作用在桩间土上的应力为

图3 桩间土受力计算图Fig.3 Calculation of vertical stress of soil between pile caps

对于三角形布桩来说，桩顶上的土拱由6 个单栱组成，桩顶土体单元见图4，在垂向上的平衡方程为

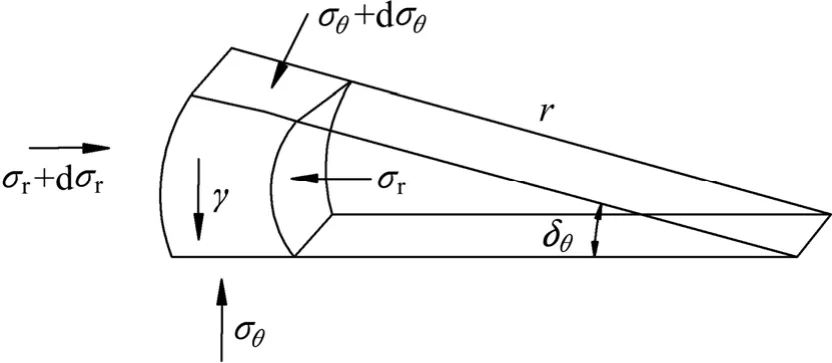
图4 桩顶单元土体受力分析Fig.4 Stress analysis of soil unit at the top of pile cap

如图5 所示，作用在桩顶土拱内侧的压力

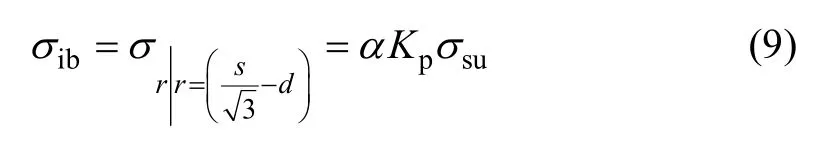
以式(9)作为边界条件解式(7)和(8)得桩顶土体环向应力 σθ为

图5 桩顶土拱内侧土压力Fig.5 Inner stress analysis of soil arch at the top of pile

由图6 所示，得单拱在桩帽上产生压力P1的积分公式为

桩帽上的总压力为单栱产生压力的6 倍，则桩顶总压力为

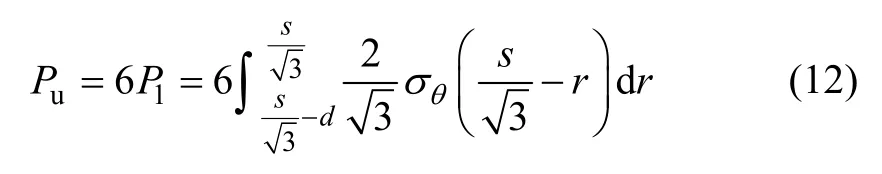
待定系数α 可有三角形布桩情况下单桩处理范围内路堤平衡方程求解，即

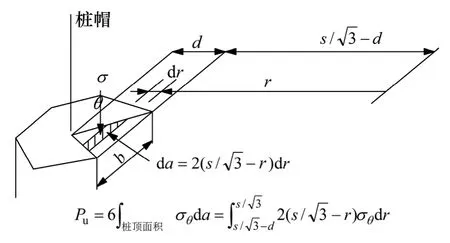
图6 桩顶土压力计算Fig.6 Earth pressure calculation at the top of pile cap

求解式(13)即可得到α ，若α ＜1，则说明土拱还未进入塑性状态；若α ＞1，则说明土拱已经进入塑性状态，土拱承受的路堤荷载比例不再增加，此时，桩土荷载分担比与α=1 时的相同。

2 加筋垫层分析

针对三角形布桩，结合本文提出的等效桩帽概念，对拉膜效应建立模型并分析。三角形布桩情况下拉膜区域如图7 所示。每个桩帽连接桩周的6 个拉膜区域，假设沿每一计算长度拉膜半径相同，均为 s/ 3- d，则拉膜在每一边上的拉力的竖向分力即为桩帽由拉膜效应所承担的荷载。

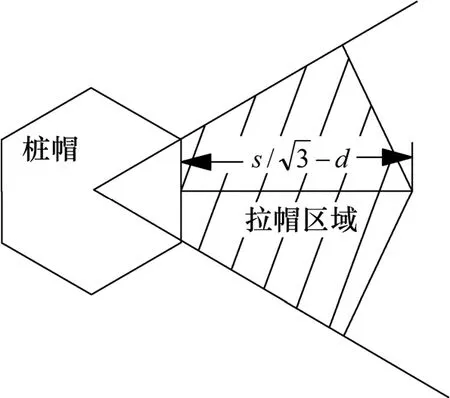
图7 拉膜效应计算示意图Fig.7 Stress calculation of tension membrane effect

先取桩间土区域加筋材料微单元进行受力分析，如图8 所示，桩间土加筋垫层整体受力分析见图9。由受力平衡得

其中：筋土间摩擦力 τ1=f1σs1，τ2=f2σs2。y 为加筋层挠度；r′为加筋垫层径向距离；σs1为垫层上部应力；σs2为垫层下部应力；t 为单位宽度垫层加筋材料拉拔力；θ 为T 与水平方向的夹角；f1和f2分别为垫层与上覆土层和下覆土层之间的摩擦因数；τ1和 τ2分别为垫层与上覆土层和下覆土层之间的摩擦力。

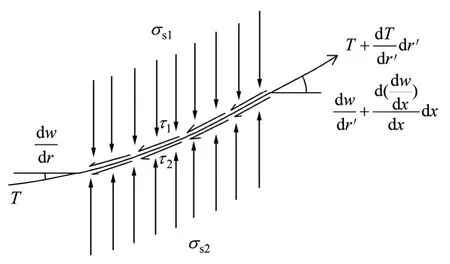
图8 加筋材料单元体受力分析Fig.8 Stress analysis of reinforced material unit

图9 桩间土区域加筋材料整体受力分析Fig.9 Integral stress analysis of reinforced material in area between piles

设在上覆填土的重力作用下，加筋垫层产生的弯沉沿径向呈抛物线状，下凹的最大挠度即桩土最大沉降差Δs，为拉膜最低点，可由计算或实测数据得到。如图9 所示的直角坐标系，则抛物线方程为

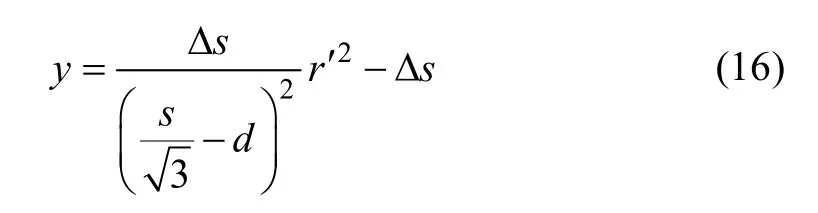
假设地基土反力服从Winkler 弹性地基：

式中：K 为基床系数，kN/m3。

联立式(14)～(17)，解得

由此可得桩帽边缘处单位宽度加筋材料拉拔力为

桩帽上承担的拉拔力即为桩帽周长范围内拉拔力之和，即加筋材料在桩帽边缘处的单位宽度拉拔力与桩帽周长的乘积，得桩帽承担总拉力

值得注意的是，在Δs 较小的情况下，由式(21)得到的桩帽承担总拉力影响不大。

将土拱效应与拉膜效应相结合，即令 σs1=σsu，Pu为仅在土拱作用下桩顶承担荷载，则在2 种效应共同作用下桩间土所受平均土压力为

桩体荷载分担比为

3 工程实例验算

珠江三角洲环形高速公路西环段(南段)高速公路是国道主干线广州绕城公路九江至小塘段，属于国家重点项目[15]。工程试验段设在西二环段四标(K9+509.8)～(K9+555.3)(宽55.0 m，长50.0 m)范围内，软基层厚18～20 m，堤身填土为素填土，压实后重度约为18.5 kN/m3，内摩擦角为30°。填土厚5.0 m。桩长20.0 m，路基桩间距3.0 m，锥坡桩间距3.5 m，呈正三角形梅花式满堂红布置，桩顶设置C25 钢筋混凝土桩帽(长×宽×高为1.5 m×1.5 m×0.2 m)。

桩体荷载分担比的计算值与实测值比较如图10所示，在填土高度为2 m 时，计算得到桩体荷载分担比为0.41，实测值为0.52，计算值略小于实测值。随着填土高度的增加，两者逐渐趋于接近，在填土高度达到5 m 时，计算值为0.84，实测值为0.83。

图10 桩体荷载分担比比较Fig.10 Comparison of pile efficacies of calculation and practical engineering

值得注意的是计算结果在填土达到4.65 m时即进入水平状态，这说明填土高度已达到土拱进入塑性的高度，因此，桩体荷载分担比不再增加，而实测结果表明此时的桩土应力分担情况仍有缓慢变化，但差距较小，仍可说明本文的桩体荷载分担比计算方法有一定的正确性。

4 参数分析

4.1 Kp 变化的影响

取桩帽宽度b 与桩间距s 之比δ等于1/3 不变，路堤填料的郎肯被动土压力系数Kp分别为2，3 和4，计算桩体荷载分担比随桩间距的变化，如图11 和12所示。结果表明：在Kp不等时，填土较低时桩体荷载分担比相同，随着填土高度的增加，到一定程度后，Kp较小的土拱先达到稳定值，即此时土拱进入塑性状态，桩体荷载分担比不再增加。由此说明随着Kp的增大，桩体荷载分担比最大值逐渐增大，这说明在路堤土拱范围内采用内摩擦角较大的填料，有助于更好地发挥桩体的荷载分担作用。对比图11 和图12 可见：在Kp和δ相等的情况下，桩体荷载分担比在仅考虑土拱作用下的值要小于同时考虑土拱拉膜作用下的值，并且2 种情况下达到最大值时的s/H 相等。

4.2 δ变化的影响

路堤填料的郎肯被动土压力系数Kp=4，取桩帽δ分别为1/2，1/3 和1/4，计算桩体荷载分担比随桩间距的变化，如图13 和图14 所示。从图13 和图14 可见：桩体荷载分担比随着δ的增大而增大，且δ较小的土拱在s/H 较低时即进入塑性状态。这说明在实际工程中合理控制桩帽大小和桩间距范围，对路堤的合理受力有较大影响。对比图13 和图14 可见：与Kp变化的情况下相似，同时考虑土拱拉膜作用下的桩体荷载分担比较大。

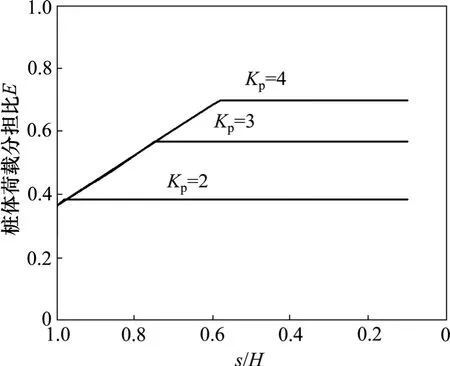
图11 土拱作用下桩体荷载分担比随Kp 的变化Fig.11 Variation of pile efficacy with coefficient of passive earth pressure(Kp)under soil arching effect

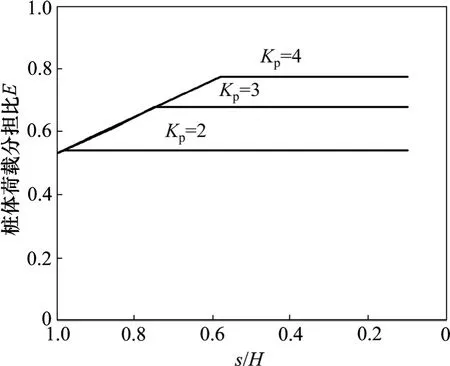
图12 土拱拉膜共同作用下桩体荷载分担比随Kp 的变化Fig.12 Variation of pile efficacy with coefficient of passive earth pressure(Kp)under soil arching effect and tension membrane effect

图13 土拱作用下桩体荷载分担比随δ的变化Fig.13 Variation of pile efficacy with ratio of pile cap dimension to pile spacing(δ)under soil arching effect

图14 土拱拉膜共同作用下桩体荷载分担比随δ的变化Fig.14 Variation of pile efficacy with ratio of pile cap dimension to pile spacing(δ)under soil arching effect and tension membrane effect

5 结论

1) 针对三角形布桩情况，提出等效桩帽的概念，依据三角形布桩下桩土荷载分担规律对“土拱效应”和“拉膜效应”进行了公式推导，进而得到桩承式加筋路堤下桩土荷载分担比的计算方法。

2) 在同等条件下，路堤桩体荷载分担比随路堤填料的郎肯被动土压力系数Kp和桩帽宽度与桩间距之比δ的增大而增大，同时考虑“土拱效应”和“拉膜效应”共同作用下的桩土应力的差异显著大于仅考虑“土拱效应”的桩土应力差异。

3) 填土高度较低时桩体荷载分担比实测值略大于计算结果，随着填土高度的增加，两者趋于接近。这说明本文提出方法计算的结果与工程实际较接近，切实可行。

[1] Terzaghi K. Theoretical soil mechanics[M]. New York: Jhon Wiley and Son,1943:66-75.

[2] Carlsson B. Reinforced soil principles for calculation[M].Linoping:Linoping University,1987.

[3] Low B K,Tang S K, Choa V.Arching in piled embankments[J].Journal of Geotechnical Engineering, ASCE, 1993, 120(11):1917-1938.

[4] Hewlett W J, Randolph M F.Analysis of piled embankments[J].Ground Engineering,1988,21(3):12-18.

[5] 陈云敏, 贾宁, 陈仁朋. 桩承式路堤土拱效应分析[J]. 中国公路学报,2004,17(4):1-6.CHEN Yunmin,JIA Ning, CHEN Renpeng. Soil arch analysis of pile-supported embankments[J]. China Journal of Highway and Transport,2004,17(4):1-6.

[6] 陈仁朋, 贾宁, 陈云敏. 桩承式加筋路堤受力机理及沉降分析[J]. 岩石力学与工程学报,2005,24(23):4358-4367.CHEN Renpeng, JIA Ning, CHEN Yunmin. Mechanism and settlement analysis of pile-supported and geogrid-reinforced embankments[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(23):4358-4367.

[7] 吕伟华, 缪林昌, 王非. 基于不完全土拱效应的土工格栅加固机制与设计方法[J]. 岩石力学与工程学报, 2012, 31(3):632-639.LÜ Weihua, MIAO Linchang, WANG Fei. Mechanism of geogrid reinforcement based on partially developed soil rich effect and design method[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(3):632-639.

[8] 蔡德钩, 闫宏业, 叶阳升, 等. 桩网支承路基结构中土拱效应及网垫受力的模型试验研究[J]. 铁道学报, 2011, 33(11):85-92.CAI Degou,YAN Hongye,YE Yangsheng, et al.Model study on arch effect and bedding force of geosynthetics reinforced and pile supported embankment[J]. Journal of the China Railway Society,2011,33(11):85-92.

[9] 强小俊, 赵有明, 胡荣华. 桩网结构支承路堤土拱效应改进算法[J]. 中国铁道科学,2009,30(4):7-12.QIANG Xiaojun, ZHAO Youming, HU Ronghua. Improved algorithm for the soil arching effect of pile-net supported embankment[J].China Railway Science,2009,30(4):7-12.

[10] 费康, 王军军, 陈毅. 桩承式路堤土拱效应三维分析[J]. 土木建筑与环境工程,2012,34(5):77-84.FEI Kang, WANG Junjun, CHEN Yi. A three dimensional simplified method for analysis of soil arching effect in the pile-supported embankments[J]. Journal of Civil, Architectural and Environmental Engineering,2012,34(5):77-84.

[11] 陈福全, 李阿池, 吕艳平. 桩承式路堤中土拱效应的改进Hewlett 算法[J]. 岩石力学与工程学报, 2007, 26(6):1278-1283.CHEN Fuquan, LI Achi, LU Yanping. An improved solution of Hewlett’s method for soil arching effect on piled embankments[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(6):1278-1283.

[12] Kempfert H G, Berhane G. Excavations and foundations in soft soils[M].Netherlands:Springer Verlag,2006:18-40.

[13] Giroud J P, Bonaparter, Beech J F, et al. Design of soft layer-geosynthefic systems overlying voids[J]. Geotextiles and Geomembrane,1990,9(1):155-160.

[14] 陈娟, 吴西臣. 桩网复合地基桩土应力比的确定[J]. 水文地质工程地质,2007(3):116-119.CHEN Juan, WU Xichen. Determination of the stress ratio of pile and soil of pile-net composite foundation[J]. Hydrogeology&Engineering Geology,2007(3):116-119.

[15] 夏唐代, 王梅, 寿旋, 等. 筒桩桩承式加筋路堤现场试验研究[J]. 岩石力学与工程学报,2010,29(9):1929-1936.XIA Tangdai, WANG Mei, SHOU Xuan, et al. Field test of reinforced embankment supported by cast-in-situ thin-wall tubular piles[J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(9):1929-1936.