浅析混合气体温度的分子动力学

霍颖柳，苏妙兰，卜寿亮，黄真贤，刘玉峰，陈 彪，朱姗姗

(嘉应学院物理与光信息科技学院，广东梅州514015)

0 引言

根据经典分子动力学理论［1，2］，物质的温度与构成物质的原子或分子无规则热运动的剧烈程度密切相关.物质的温度越高，相应的原子或分子的热运动越快;反之，物质的温度越低，相应的原子或分子的热运动越慢.目前，人们想当然地认为，质量相同、温度分别为T1、T2的同种类的气体，所含的分子N1、N2仍然相等，且它们混合后，达到平衡时的温度是它们原来温度之和的一半.那为什么会得出这样的结果呢?那是因为人们都认为:两质量相同、温度分别为T1、T2的同种类的气体的分子数相同，即N1=N2=N，

则分子平均平动动能分别为［3～6］:

则气体的分子总动能为:

将温度分别为T1、T2的同种类的气体混合，设它们混合后的分子总动能为为混合后的分子平均平动动能).

由能量守恒可知，混合前的分子总动能与混合后的分子总动能相等，所以有

即

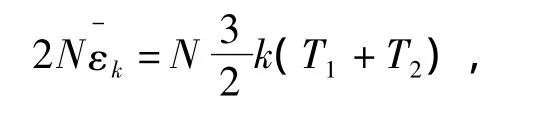
由于混合后的分子平均平动动能为:

我们发现，众多的国内、外教材都想当然地认为结果如上所述，几乎所有的老师和学生也都对此深信不疑.

然而，根据狭义相对论［7，8］，物质的质量随速率的变化而变化，故对于相同宏观质量，不同温度的同种气体，温度高意味着具有更大的平均分子运动速率，相应分子运动质量也会随之变大，反之，温度低时，相应的运动速率变小，分子运动质量也将随之变小.于是，我们可以知道不同温度的同种气体在宏观质量相同的情况下，分子的数目应该不相同，因此推出T=(T1+T2)/2的结论的前提已不再成立了.本项目将结合分子动力学和狭义相对论，对此问题进行探索、分析和论证.

1 计算在相同质量、不同温度下同种气体所含的分子数

我们先取质量同为M，温度分别为T1、T2的同种气体，假设气体都处于热平衡状态，根据麦克斯韦速率分布律［3～6］，有

根据狭义相对论［4］:

当v∈(0，c)时，上式有意义.

由(2)式质速方程我们知道，分子的质量是随着分子运动速率的变化而变化，而麦克斯韦速率分布函数即(1)式是在分子的质量不变的情况下得到的，所以麦克斯韦速率分布函数中的归一化常数C将发生变化.我们对麦克斯韦分布速率函数(1)式进行修正有:

其中，C0(T)是新的归一化常数.

设m0为单个气体分子的静止质量，N为总的分子数，根据麦克斯韦速率分布律，处在速率为v～v+dv区间内的气体分子总质量为

将(3)式代入(5)式得

由速率分布函数的归一化条件可得

所以，新的归一化常数C0(T):

将(2)式代入(6)式得

根据(9)式，画出下图1所示的曲线，该曲线形象地描述出气体分子数N与温度T之间的关系:随着温度的变化，气体的分子数也在不断变化.而不是人们所认为的那样:质量相同的气体无论温度如何改变，分子数都不变.

2 在狭义相对论的基础上重新建立更为精确的温度微观表达式

由分子动力学理论中的温度微观表达式可知，气体分子的平均平动动能只与温度有关，并与热力学温度成正比，即:，则对于速率在o～ c范围内的气体分子的平均平动动能为

由(2)、(3)、(10)式，我们可得到更为精确的温度微观表达式所应满足的方程如下:

3 物质混合前后温度的变化规律

假设同种气体的温度分别为T1、T2，总分子数分别是N1、N2，则它们的分子平均平动动能分别为

混合前的同种气体分子总动能为

令N1=λN2，因为我们从前面的N－T图像可知，在不同温度下，质量相同的同种气体所含分子数不同，即令N1≠N2，所以λ≠1.

将N1=λN2代入(13)式可得:

进而，由于T1≠T2，λ≠1，

即

故

4 结论

本文首先论证了质量相同、温度分别为T1、T2的同种气体的分子数不相同，推翻了T=(T1+T2)/2成立的前提条件，进而经过进一步的推导，证明出混合达到热平衡后的温度T≠(T1+T2)/2.同时，在此基础上建立了更加精确的温度微观表达式所应满足的方程.

［1］张志杰.分子动力学方法计算气体的物理性质［D］.秦皇岛:燕山大学，2010:1－10.

［2］蓝建慧.从头计算分子动力学方法及其应用［J］.石油大学学报，2005，29(4):143－146.

［3］李椿，章立源，钱尚武.热学［M］.2版.北京:高等教育出版社，2008:44－61.

［4］漆安慎，杜婵英.力学［M］.2版.北京:高等教育出版社，2005:421－440.

［5］汪志诚.热力学·统计物理［M］.3版.北京:高等教育出版社，2003:246－261.

［6］张辉，刘德磊.经典热力学发展概述［J］.广州化工，2012，40(2):26－28.

［7］张元仲.狭义相对论实验基础［M］.北京:科学出版社，1994:51－63.

［8］黄志洵.论狭义相对论的理论发展和实验检验［J］.中国工程科学，2003，5(5):7－17.