邯郸市百日咳发病的气象流行病学特征统计分析

赵鲜芝 李燕霞 王洪 果丽平

人类的生活方式近年来发生着巨大的改变，对地球的气候造成了空前的影响，进而可能会引起传染病发病率及其地理分布的重大变化。天气模式的变化，以及由此造成的健康方面的负面影响，可能在全球将非常严重［1］。本文运用气象流行病学原理和方法对1972至2010年气象因素与百日咳发病率关系进行研究，查找科学的统计分析方法，探讨百日咳发病的气象流行病学特征。

1 资料与方法

1.1 一般资料

1.1.1 疫情资料:1972至2010年邯郸市百日咳病例按月报告发病数和发病率资料，由邯郸市疾病预防控制中心疫情信息科提供。

1.1.2 人口资料:1972至2010年邯郸市人口资料，由邯郸市统计局提供。以常住本地人口的病例纳入统计。

1.1.3 气象资料:1972至2010年邯郸市气象资料，包括月平均气温、月平均气压、月平均相对湿度、月平均风速、月日照时数、月总降雨量、月极端最高气温、月极端最低气温、月小型蒸发量、月平均总云量等10个气象因素，由邯郸市气象局提供。

1.2 方法 建立数据库:将疫情数据、气象资料和人口资料数据采用EpiData进行“双重录入”，再由SPSS导入，建立数据库。

1.3 统计学分析 应用SPSS 17.0统计软件，相关分析、曲线估计、曲线拟合、因子分析、主成分多元回归分析等。

2 结果

2.1 气象参数 对月平均气温、月平均气压、月平均相对湿度、月平均风速、月日照时数、月总降雨量、月极端最高气温、月极端最低气温、月小型蒸发量、月平均总云量等10个气象参数做正态性检验，其中月日照时数和月平均总云量服从正态分布，其他8个气象参数均不服从正态分布。对这10个气象参数做共线性诊断，结果本组气象参数数据容差最小为0.014，方差膨胀因子最大达69.998。

2.2 百日咳发病情况1972年1月至2010年12月，邯郸市报告百日咳病例83 003例，平均月报告发病率为2.44/10万。经单样本Kolmogorov-Smirnov检验(P＜0.01)，发病呈偏态分布;极差为87.33，四分位数间距为0.461。1972至1977年百日咳发病水平较高，最高达86.42/10万，1978年开始百白破疫苗实行计划免疫，1978至1982年发病水平不断下降，1983年开始发病水平始终维持在0.50/10万以下。见图1。

2.3 相关分析 采用Spearman相关分析，结果显示，邯郸市1972至2010年百日咳月发病率与月小型蒸发量、月平均风速、月日照时数之间的相关系数差异有统计学意义(P＜0.01)。其中月平均风速与百日咳月发病率的相关系数最大，为0.425。百日咳月发病率与这3个气象因素均呈正相关。

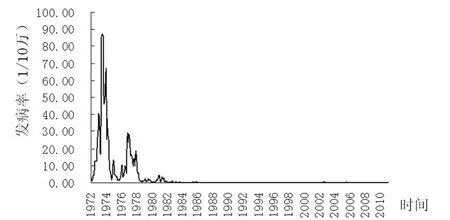
图1 邯郸市1972～2010年百日咳月发病率

2.4 曲线估计 将百日咳疫苗计划免疫前后的百日咳发病率所构成的曲线趋势，分段进行曲线估计。结果发现EPI前百日咳月发病率的三次模型的决定系数最大，R2值为0.379，F值为13.804，P＜0.001，方程为=-5.921+5.068X-0.177X2+0.002X3。EPI后百日咳月发病率的倒数模型的决定系数最大，R2值为0.599，F值为588.251，P＜0.01，方程为=0.090+9.461/X。所以认为，EPI之前百日咳月发病率呈3次模型曲线，之后百日咳月发病率呈倒数模型曲线。

2.5 曲线拟合1972至2010年的百日咳月发病率作为因变量，10个气象因素分别作为自变量，进行曲线拟合，进一步研究气象因素与百日咳月发病率的定量关系。在10个方程中，月平均气温和百日咳月发病率拟合为线性方程，月平均风速和百日咳月发病率拟合为二次方程，月平均相对湿度、月总降雨量、月极端最高气温、月极端最低气温、月小型蒸发量、月日照时数和百日咳月发病率拟合为三次方程。月平均气压和百日咳月发病率拟合为倒数方程，月平均总云量和百日咳月发病率拟合为对数方程。月平均风速、月小型蒸发量、月平均总云量、月日照时数的R2值分别为0.050、0.042、0.015、0.026，P值分别为 ＜0.001、＜0.001、0.015、0.017，故认为月平均风速的曲线拟合结果较理想。百日咳月发病率与月平均风速的二次方程曲线关系得到曲线拟合方程，=-0.227+0.186X+0.019X2。

2.6 因子分析

2.6.1 气象参数的KMO和Bartlett检验结果:KMO值为0.839，表示非常适合做因子分析;Bartlett球形度检验的P＜0.001，因此拒绝原假设，说明变量间存在相关关系，适于因子分析。

2.6.2 因子贡献率结果:10个因素中可得到两个因子Z1和Z2，特征根分别为 λ1=5.591，λ2=2.381，且其对总方差的累积贡献率为79.717%，其余特征根均小于1，因此提取前两个因子作为主因子。

2.6.3 主成分多元线性回归:以月发病率作为因变量，因子分析所得两个主因子Z1和Z2作为自变量，采用逐步回归法建立多元线性回归方程(aλ=0.05，a出=0.10):=5.326+0.461Z2，回归方程决定系数R2=0.064，调整R2=0.057，对方程检验，F=9.282，P=0.003，差异有统计学意义。

3 讨论

许多学者为探讨气象因素和传染病之间的关系，采用了不同的统计方法，包括等级聚类分析、时间序列泊松回归、Spearman等级相关分析、多元时间序列分析方法、互相关分析、多元线性回归等［2-6］。其中Spearman等级相关分析是较常用的一种［7，8］。目前多元线性回归分析方法已被广泛应用于因果关系的研究中。但是本研究显示气象参数间存在严重的多重共线性，极为影响回归分析的效果。因此多重共线性问题是回归分析中需注意的一个重要方面，做多元回归分析时有必要进行共线性诊断［9］。

多重共线性问题的解决办法之一是进行因子分析或主成分分析。对本文的气象参数做KMO统计量和Bartlett球型检验，显示十分适合做因子分析。结果显示，虽然两个主因子Z1、Z2和百日咳月发病率之间建立起了多元回归方程，且方程有统计学意义，但其调整R2值太低(0.057)，拟合效果较差，提示气象因素对百日咳发病的影响在总的影响因素中占的比例很小。

Spearman相关分析结果显示，邯郸市1972至2010年百日咳月发病率与月小型蒸发量、月平均风速、月日照时数之间均呈正相关(P＜0.01)。其中月平均风速与百日咳月发病率的相关系数最大，是影响百日咳发病的主要气象因素。从曲线估计结果可以看出，开展百日咳疫苗计划免疫之前百日咳月发病率呈三次模型曲线，之后呈倒数模型曲线，可见计划免疫对百日咳发病率的影响非常大。从曲线拟合结果得出，百日咳与月平均风速的曲线拟合结果较理想，百日咳与月平均风速呈二次方程曲线关系，提示月平均风速是影响该病的主要气象因素，这和李秀昌等人的研究结果相同［7］。而曲波等［8］报道辽宁市朝阳地区的百日咳发病率和年平均气压及平均蒸发量相关，本文结果与其不符，原因有待进一步探讨。

1 Amy Greer PhD，Victoria Ng BS，David F.Climate change and infectious diseases in North America:the road ahead.CMAJ，2008，178:715-722.

2 Zhang WY，Guo WD，Fang LQ，et al.Climate variability and hemorrhagic fever with renal syndrome transmission in Northeastern China.Environ Health Perspect，2010，118:915-920.

3 Huang F，Zhou SS，Zhang SS.Temporal correlation analysis between malariaand meteorological factors in Motuo County，Tibet.Malaria J，2011，10:54-56.

4 Fang LQ，Wang XJ，Liang S，et al.Spatiotemporal trends and climatic factors of hemorrhagic fever with renal syndrome epidemic in Shandong Province，China.PLoS Negl Trop Dis，2010，4:789-790.

5 Xiao D，Long Y，Wang SQ，et al.Spatiotemporal distribution of malaria and the association between its epidemic and climate factors in Hainan，China.Malaria Journal，2010，9:185-188.

6 Zhou SS，Huang F，Wang JJ，et al.Geographical，meteorological and vectorial factors related to malaria re-emergence in Huang-Huai River of central China.Malaria J，2010，9:337-339.

7 李秀昌，孙健，胡亚男.长春地区气候与传染病间关系分析.中国卫生统计，2010，27:66-69.

8 曲波，关鹏，周宝森，等.干旱地区气象因素对常见传染病疫情影响的研究.中国医科大学学报，2004，33:35-39.

9 丁元林，孔丹莉，毛宗福.多重线性回归分析中的常用共线性诊断方法.数理医药学杂志，2004，17:299-300.