低雷诺数下进气道异常起动现象及其影响因素探析

2014-03-30 06:32李祝飞肖丰收姜宏亮刘坤伟高文智杨基明

实验流体力学 2014年4期

凌岗, 李祝飞, 肖丰收, 姜宏亮, 刘坤伟, 高文智, 杨基明

(1. 中国科学技术大学近代力学系, 合肥 230027; 2. 中国空气动力研究与发展中心, 四川绵阳 621000)

0 引言

与层流相比，湍流因其既有可能造成显著增加摩阻、热流等弊端又具有抑制分离、增强混合等潜在优势的双重特点而常常成为飞行器，尤其是高超声速飞行器研制中一个十分微妙的考虑因素。一般来说，从飞行器外流的气动力(摩阻)/气动热(热流)角度考虑，多将湍流影响作为不利因素而尽量推延其产生过程；而另一方面，从内流的进气道起动以及燃料混合等角度考虑，却又往往设法强化其影响和作用。作为冰山一角，本文以进气道起动问题为关注点，在给出近期观测到的低雷诺数实验中一些新结果的同时，也力图对其中的机理问题进行探讨和分析。

进气道“起动”状态，一般来说是指当进气道内部的流动现象没有改变进气道流量捕获特性时，进气道是起动的[1]。引起进气道不起动的主要因素有：来流马赫数过低，捕获的流量难于全部通过喉道；激波边界层等复杂干扰引起分离，造成流动壅塞；反压过高，超出隔离段承受能力等等[2]。特别是流动分离引起的进气道入口处壅塞，是最基本也是最复杂的一个问题。此外，在压缩面的高逆压梯度区(如压缩拐角)的层流分离也会促使流场恶化并降低进气道捕获而影响性能。为了抑制流动分离，一般期望进气道入口处的流动为湍流流动。因此，采用转捩带来实现强制转捩也就成为高超声速进气道研制中最为普遍的措施之一[3-4]。由于地面实验多采用缩尺模型，不同设备雷诺数往往差异较大[5]，实际飞行中雷诺数随高度和速度也会有较大变化，加之进气道流动中上下游耦合效应明显，使得强制转捩以及分离控制过程比一般的简单构型要复杂得多。

作者在前期的研究中，对进气道不同缩尺条件下的起动情况进行了比较，结果表明进气道模型尺度缩小，进气道起动性能会有所降低，并指出了雷诺数是导致缩尺模型起动性能降低的主要原因[6]。本文在此基础上，针对近期所发现的很低雷诺数条件下进气道反而呈现起动特征的异常现象开展了进一步的考察和计算模拟分析，旨在对其机理能获得较为合理的认识。

1 实验与计算方法

实验在中国科学技术大学激波实验室的KDJB-500激波风洞进行，为了抑制激波风洞运行初期的非定常效应对进气道起动的辅助作用，在进气道出口预先设置轻质堵块来模拟进气道自起动实验[7]。实验中采用的是高超声速二元混压式进气道，外压段采用两级压缩，唇口为尖前缘设计，内收缩比为1.77，通过前后移动唇口位置可以改变进气道内收缩比。图1给出了实验中采用的进气道模型，模型总长度440mm，宽度为54mm，隔离段高度为10mm，其它具体尺寸参照文献[8]。实验来流马赫数为M∞=5.9，基准单位雷诺数为Reref=5.1×106m-1，实验中保持总温为810K不变，通过变化来流密度即变化总压来改变实验单位雷诺数。实验中采用高速纹影[8]观测流场来判别进气道的起动特性。

图1 二元进气道实验模型

计算采用Fluent商用软件进行N-S方程数值求解，湍流模型选择S-A模型，通量格式采用AUSM格式。边界条件采用压力远场条件、压强出口条件和等温无滑移固壁，粘性系数采用Sutherland公式计算。计算以低马赫数(如M∞=3)得到进气道不起动流场，然后以上一步的收敛解作为初场，逐步增加来流马赫数进行续算，直至进气道起动，所对应的马赫数即为自起动马赫数[9]。为便于实验验证，本文采用激波风洞实验中M∞=5.9条件相同的动压和总温配置得到各马赫数下的来流条件。

2 低雷诺数下进气道异常起动实验结果

为研究雷诺数对进气道起动的影响，对进气道在不同单位雷诺数下进行了一系列的实验研究。图2给出了基准单位雷诺数条件下进气道自起动实验纹影(t′+0对应于激波风洞实验段流场开始建立的时刻)。从图中可以看出，在气流进入进气道时(0.35ms)，由于轻质堵块的堵塞作用，气流被推出进气道，进气道处于不起动状态(1.45ms)；当轻质堵块被吹走，进气道恢复畅通，即引起进气道不起动的因素消除之后，分离激波随即被吞入隔离段，进气道又能够迅速建立起稳定的超声速流场(7.95ms)，表明在此状态下进气道能够实现自起动。在此后的试验时间内，波系结构一直很稳定，进气道始终保持着起动状态(10.5ms、13ms、17.5ms)。

以图2结果为参照基准，在不断降低来流单位雷诺数的条件下重复上述实验。图3分别给出了单位雷诺数降低到基准单位雷诺数的1/2和1/3时的纹影显示结果。从图中可明显看出，当单位雷诺数降低到基准单位雷诺数的1/2时，在轻质堵块被吹除和隔离段恢复畅通之后，进气道入口始终有大范围的分离存在，隔离段内无法形成稳定的超声速流场。也就是说，此时进气道不能实现自起动(图3(a))，这与通常所建立的进气道起动能力随雷诺数降低而下降的认识相一致[6]。

图2 基准单位雷诺数下进气道自起动过程纹影照片

然而，当单位雷诺数进一步降低到基准单位雷诺数的1/3时，在堵块被吹除后，隔离段内又重新建立起超声速特征十分明显的波系结构(图3(b))，从这一流场结构判断，进气道此时又呈现出自起动的特征。这与作者的最初预期(即降低雷诺数应该不能自起动)刚好相反，而且反复实验的结果均重复了上述异常起动现象。以基准单位雷诺数条件下的进气道正常起动结果(图2)为参照，对比低雷诺数下的异常起动流场(图3(b))，其波系差异并不十分明显，只是图3(b)的波系与下壁面的反射作用区域有一定的外移，表明该处存在相对较厚的局部低速流动区域；另外，通过仔细观察高速纹影动画也可发现，尽管超声速流场起主导作用，但仍可看出其波系结构存在些许波动，读者可从图3(b)中不同时刻纹影照片(17.7ms、18.8ms、19.6ms、24.5ms)的细微差异来判别。

(a) 1/2Reref

(b) 1/3Reref

上述异常起动现象与目前已有的相关概念，即雷诺数降低不利于进气道起动的认识[6]出现了明显的矛盾。因此，不论是从流动控制还是认识规律的角度，探明其机理无疑是十分必要的。

3 异常起动现象机理和影响因素分析

3.1流态影响模拟分析

考虑到实验中采用的模型尺度较小，在低单位雷诺数下，前体压缩面边界层更趋于层流状态，而通常的认识则是层流更不利于进气道起动。不过在以往的研究中，大多关注的是湍流状态，对层流状态下的进气道起动特性尚未见到较为系统的文献报道。为此，有必要对低雷诺数条件下层流和湍流的流态影响进行一定的分析探讨。

为便于和实验结果比较，分别对不同单位雷诺数条件时的流场进行了自起动数值模拟，在基准单位雷诺数和单位雷诺数降低到1/2时选择湍流S-A模型，而在单位雷诺数降低到1/3时则选择层流和湍流模型同时进行对比计算。图4分别给出了不同单位雷诺数下的数值纹影结果。通过与图2和图3的实验结果对比可以发现，图4(a)-(c)的数值纹影结果与相应条件下的实验纹影照片有较高的吻合度，特别是在图4(c)的层流状态下，计算和实验结果(见图3(b))高度地相似，进气道呈现明显的起动状态，只是较基准单位雷诺数时，下壁面的低速流区域更加明显。与之相比，图4(d)所采用的湍流模型计算结果与实验(图3(b))的差异则非常明显。

(a) 1Reref, 湍流(S-A)数值纹影

(b) 1/2Reref, 湍流(S-A)数值纹影

(d) 1/3Reref, 湍流(S-A)数值纹影

可见，从数值结果来看，当单位雷诺数降低到1/3时，在湍流流态下进气道是明显的不起动状态，而在用层流模型计算时，进气道反而呈现出起动状态，而且流场结构和实验照片也有着较高的吻合度。这一结果更促使作者将注意力转向流态的影响方面。

3.2强制转捩实验考察

为进一步考核异常起动是否与层流相关，将来流条件设定为基准单位雷诺数的1/3，通过添加转捩带进行强制转捩，再次进行模型进气道的自起动实验考察。转捩带采用的是一种菱形扰流器，在压缩拐角上游(即第一级压缩面)不同位置添加形状为3mm×3mm，厚度为1.5mm的正方形扰流器组成的转捩带，来促进层流边界层向湍流边界层转捩[10]。每组转捩带由流向相距10mm、展向间距5mm的2×10扰流器阵列组成。图5给出了转捩带添加方式示意图，为获得不同的强制转捩效果，在距前缘10mm的上游和距压缩拐角10mm的下游可分别安置一组或同时安置两组转捩带以考察其对进气道起动的影响。

图6是添加转捩带后的实验结果。其中图6(a)为本实验中扰动效果最强的上下游同时安置转捩带的情况。从该纹影图中可以看出，此时显然进气道不能实现自起动。对比相同来流条件下未加扰动的图3(b)的实验结果不难发现，二者流场结构差异显著，因为前者呈现的是自起动状态。而另一点需要指出的则是，此时的流场结构(图6(a))与相同来流条件下的湍流数值模拟结果(图4(d))却有着相似之处。也就是说，采取了较强的强制转捩措施之后，所得到的流场结构与湍流的数值模拟相一致，均表明进气道处于不能自起动的状态。

图5 添加扰流器后的进气道模型

图6(b)～(c)所示实验结果是在相对扰动较弱的、只添加一组强制转捩带的条件下得到的，其中图6(b)和(c)分别对应仅在第一级压缩面的上游和下游添加扰流器的情况。有意思的是，虽然二者实验条件的差别仅仅只是扰流器的位置略有不同，但与之对应的进气道自起动特性却出现了两极分化：前者显然处于不能自起动的状态，而后者则表现出自起动的特征。换言之，在接近前缘处添加一组转捩带达到了与上下游同时安置两组转捩带相当的效果(见图6(b)和图6(a))，而仅在接近压缩拐角的下游处安置转捩带则与未采取强制转捩措施的结果相近(见图6(c)和图3(b))。关于下游强制转捩带效果不明显的原因将在后文中结合相关的数值分析进行讨论。需要强调的是，作者为排除偶然因素所带来的随机性，经过多次重复实验，所得到的结果都是一致的。

(a) 上下游同时加转捩带

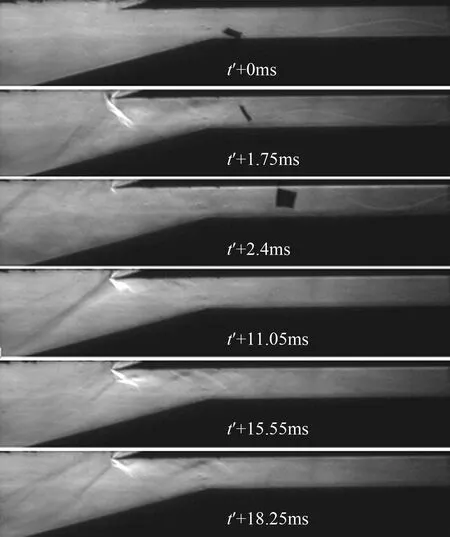
(b) 仅上游加转捩带

上述结果表明，在本实验的低雷诺数条件下，通过采取强制转捩的措施，实现了进气道由起动特征向不起动特征的转变。这一结果进一步支持了前文数值分析所得出的结论，即在雷诺数很低的情况下，层流模型所计算得到的进气道流场呈现自起动特征，而湍流模型则反之。显然，这与常规高超声速进气道助起动的概念相矛盾。因为在已有的研究中，通常的目的是促使层流边界层向湍流边界层转捩，以有利于抑制分离并提供入口畅通的进气道起动条件，这在诸如X-43A及X-51A等相关研究已经有着非常广泛的应用[11-14]。因此，对于本实验所观察到的这类异常起动现象的内在本质及其机理无疑有必要进行深入的探讨。

3.3异常起动的机理探讨

前文通过强制转捩以及层流与湍流流场的模拟分析，均表明流态影响应该是低雷诺数下进气道异常起动问题的关键因素；另外，与实验结果的吻合也为数值模拟的合理性提供了有力的支持。鉴于数值结果中含有丰富的信息，这给进一步的机理探讨提供了有价值的素材。这里重点针对两个需要澄清的问题进行探讨：一是为什么层流条件下进气道反而会呈现起动特征，其机理是什么？二是实验中所观察到的异常起动现象是否属于真正意义上的起动？

图7 给出了1/3基准雷诺数条件下，分别采用层流和湍流(S-A)模型计算得到的前体进气道流场沿对称面的马赫数分布。图中除了马赫数的信息之外，激波和分离区的结构也较为直观地显示出来。从图7(a)的层流数值结果可以看出，进气道入口处的主体结构与实验所观察到的所谓起动状态相符，尤其是入口的唇口上部，唇口激波延伸到接近喉部的大部分区域，表现出良好的畅通状态；与之相比，采用湍流模型计算得到的结果(图7(b))则不同，分离泡占据着入口的大部分空间，该分离泡所带来的入口堵塞效果可以认为是造成进气道不起动的关键因素。

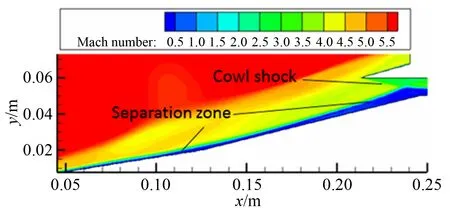
(a) 层流结果

(b) 湍流结果

下面的问题是，具有抑制分离的湍流为什么会反而造成更为恶劣的分离泡堵塞效果？通过仔细考察图7(a)的近壁流场不难发现，层流状态下并不是没有出现分离，事实上由于其更弱的抑制分离的能力，使得分离区很容易沿着壁面向上游延伸，几乎遍布整个前体压缩面区域。这种大范围的分离区对外流场所产生的效果，相当于将壁面外移，重新形成一条相对光滑的有效壁面，从而为剩余部分的入口流道提供了较为有利的通畅条件。另外，基于这一认识，也可以对前文实验中仅在接近压缩拐角的下游添加转捩带的图6(c)结果给出合理解释。由于此条件下转捩带基本淹没在分离区之中，其扰动效果难以体现，因此可以认为此时转捩带并没有达到强制转捩的目的。

对湍流来说情况则不同，其强的抑制分离的能力如果足以阻止分离泡的形成无疑将有助于进气道的起动。但是一旦不能阻止分离泡的形成，而分离区又难以向上游扩展的话，则难免会形成相对集中的激波-分离强干扰区。从图7(b)可以看出，分离泡迫使来流出现明显的向上拐折，形成较强的分离激波，该分离激波与唇口壁面作用产生的高压又反过来为分离泡的存在提供了强的逆压梯度。

因此，从这个意义上说，层流条件下，逆压梯度及时通过分离区向上游“释放”在一些特殊情况也有可能有利于维持进气道的通畅。

然而，需要强调的是，本文所观察到的异常起动现象是否属于真正意义上的起动是值得商榷的。因为进气道的起动，一般来说是指进气道内部的流动现象不改变进气道流量捕获特性[1]。但从上述讨论中可知，层流条件下前体压缩面分离区的形成无疑已经改变了进气道的流量捕获特性。因此，严格地说此时进气道并不具备起动所需要的条件，因为入口下游的流动状态是很容易通过分离区对其上游流场产生影响的，而且前体压缩面大范围的分离也迫使前体激波外移，造成入口处更多的溢流。事实上，数值计算结果表明，在图7所对应的来流条件下，尽管层流结果表现出更为通畅的流场结构，但其流量系数却仅为0.68，约为湍流结果(0.76)的89%。由此可见，这种异常的所谓“起动”状态只不过是以一种“柔和”的方式产生了溢流，而实际上是并不能被视为起动的。

为了进一步刻画层流和湍流条件下进气道在流量捕获方面的相关特征，图8给出了分别基于层流和湍流模型数值模拟所得到的流量系数随来流马赫数的变化情况。该结果对应的内收缩比同样为1.77。湍流的模拟结果表明，基准雷诺数条件下的自起动马赫数为5.8，可以看出其流量系数较为陡峭地提升，而1/3基准雷诺数条件下仍未起动。另一方面，对层流来说，尽管马赫数4以上呈现起动状态，但其流量系数不仅始终明显低于湍流的情况，而且其随马赫数的变化曲线中也未表现出湍流那样的陡峭改变。当然，层流模拟的喉道附近流场并不十分稳定，唇口激波与前体分离区的相互耦合作用会带来流场结构的些许波动，这在图3(b)和图6(c)的实验结果中也有所体现。因此，数值计算中的流量系数取值，是在喉道下游接近隔离段出口处的相对稳定部位取平均而得出的。

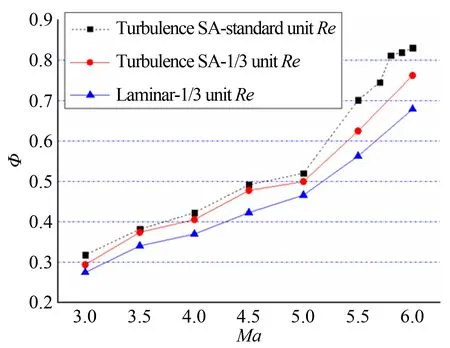
图8 不同雷诺数和两种流态下流量系数的数值结果比较

总之，流量系数的降低表明层流在流场结构上所呈现的“起动”状态并不是真正意义上的起动。其流量捕获的减少将会引起发动机性能的下降；但就流场结构而言，喉道附近和隔离段所形成的通道以及相对稳定的波系结构对燃烧室则提供了一个良好的入口环境。因此，相对于剧烈的激波边界层干扰形成分离泡及其引起的不起动状态来说尚有一定可利用的潜力。

4 结束语

通过数值模拟和实验相结合的方法，对进气道在低单位雷诺数下异常起动的现象进行了考察和机理探讨，得出以下认识：

(1) 在低单位雷诺数下，对本文的二元进气道构型来说，激波风洞的实验结果表明，会出现随着来流单位雷诺数降低又重新出现自起动特征的异常起动现象。该结果与层流模型计算得到的流场结构相符，而与湍流模拟结果差异显著。

(2) 数值模拟分析表明，层流情况下，由于分离区向前体压缩面大范围地延伸，缓解了进气道入口的逆压梯度，从而在喉道处可以形成主体为超声速的通畅流道；而湍流情况下，进气道入口处激波/边界层干扰形成过分集中的分离泡则呈现明显的壅塞状态。

(3) 尽管层流情况下进气道流场结构呈现出较为通畅的类似起动的特征，但其流量系数仍明显低于湍流的情况。因此，实验上所观察到的这种异常起动现象严格地说并不属于真正意义上的起动状态。

另外，需要说明的是，本文所观察到的流动结果是在本文实验特定构型条件下得到的，因此，对于其它不同构型的进气道来说是否出现类似情况还需要进一步研究。

参考文献:

[1]Van Wie D M, Kwork F T, Walsh R F. Starting characteristics of supersonic inlets[R]. AIAA 1996-2914.

[2]Van Wie D M. Scramjet inlet[M]. AIAA, New York, 2000.

[3]Scott A Berry, Robert J Nowak, Thomas J Horvath. Boundary layer control for hypersonic airbreathing vehicles[R]. AIAA-2004-2246.

[4]赵慧勇, 周瑜, 倪鸿礼, 等. 高超声速进气道边界层强制转捩试验[J]. 实验流体力学, 2012, 26(1): 1-6.

Zhao Huiyong, Zhou Yu, Ni Hongli, et al. Test of forced boundary-layer transition on hypersonic inlet[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(1): 1-6.

[5]Pulsonetti M V, Stalker R. A study of scramjet scaling[R]. AIAA-1996-4533.

[6]凌岗, 李祝飞, 肖丰收, 等. 一种二元高超声速进气道起动特性的尺度效应研究[J]. 实验流体力学, 2014, 28(3): 26-31.

Ling Gang, Li Zhufei, Xiao Fengshou, et al. Scale effects on the starting characteristics of a 2D hypersonic inlet[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(3): 26-31.

[7]李祝飞, 高文智, 李鹏, 等. 一种进气道自起动特性检测方法[J]. 实验流体力学, 2013, 27(4): 14-18.

Li Zhufei, Gao Wenzhi, Li Peng, et al. A test method for inlet self-starting ability detection[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(4): 14-18.

[8]李祝飞, 高文智, 李鹏, 等. 二元高超声速进气道激波振荡特性实验[J]. 推进技术, 2012, 33(05): 676-682.

Li Zhufei, Gao Wenzhi, Li Peng, et al. Experimental investigation on the shock wave oscillation behaviors in a two-dimensional hypersonic inlet flow[J]. Journal of Propulsion Technology, 2012, 33(5): 676-682.

[9]游进, 夏智勋, 王登攀, 等. 高超声速进气道再起动特性及其影响因素数值模拟[J]. 固体火箭技术, 2011, 34(2): 161-166.

You jin, Xia Zhixun, Wang Dengpan, et al. Numerical study on influencing factors of restarting characteristics for a hypersonic inlet[J]. Journal of Solid Rocket Technology, 2011, 34(2): 161-166.

[10] 黄舶, 李祝飞, 贾立超, 等. 二维高超声速进气道内激波-边界层相互干扰[J]. 中国科学技术大学学报, 2011, 41(12): 1084-1089.

Huang Bo, Li Zhufei, Jia Lichao, et al. Shockwave-boundary layer interaction in 2D hypersonic inlets[J]. Journal of University of Science and Technology of China, 2011, 41(12): 1084-1089.

[11] 战培国, 胥家常. 吸气式高超声速飞行器边界层控制研究概述[J]. 实验流体力学, 2008, 22(1): 95-100.

Zhan Peiguo, Xu Jiachang. The review of boundary layer control for hypersonic air-breathing vehicle[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(1): 95-100.

[12] Berry S, Daryabeigi K, Auslender A,et al. Boundary Layer Transition on X-43A[R]. AIAA 2008-3736.

[13] Borg M P, Schneider S P. Effect of freestream noise on roughness-induced transition for the X-51A forebody[J]. Journal of Spacecraft and Rockets, 2008,45(6): 1106-1116.

[14] Babinsky H, Li Y, Pitt Ford C W. Microramp control of supersonic oblique shock-wave/boundary-layer interactions[J]. AIAA Journal, 2009, 47(3): 668-675.

作者简介: