基于积分协方差矩阵的粒子滤波目标跟踪
顾 鑫,王 华,李 喆,李志国,王 倩,邓志均
(中国运载火箭技术研究院研究发展中心,北京100076)
1 引言
目标跟踪在众多领域都有应用,如视频监控、运动目标捕捉、飞行器自主导航等[1]。在实际应用中,目标跟踪会面临着各种环境的干扰,跟踪的鲁棒性会受到影响[2]。
目标跟踪的一个核心是选择表征目标的特征,常用跟踪算法仅选取颜色、光流等单一特征表征目标,由于跟踪系统的复杂性,单一特征跟踪鲁棒性较低[2]。本文采用一种可融合目标灰度、梯度和空间位置分布的协方差矩阵来表征目标,该特征不含特征点数量和顺序信息,对目标旋转、尺度变化及光线变化都具有较强适应性[3]。跟踪在实际应用中的另一个重要问题是计算的实时性,为了提高计算效率,本文在粒子滤波的框架下引入积分图的概念,用协方差矩阵表征目标,实现对目标的跟踪。
2 协方差区域描述子
协方差区域描述子的表征如图1所示,令I为图像帧,从I中提取一个大小为W×H×d维的特征图像:

其中,Φ表示任意一种映射,N=W×H,区域R用d×d维的协方差矩阵表示[4]:
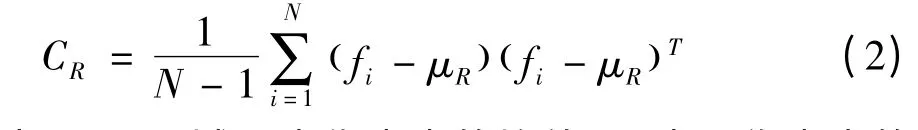
其中μR是区域R内像素点的均值;N表示像素点的数目。

图1 协方差矩阵表征目标区域示意图
3 基于协方差区域描述子的目标跟踪
3.1 积分协方差矩阵计算
粒子滤波算法中的每个粒子用协方差矩阵来表征,计算复杂度太高,难以实现实时运算,为了实现快速计算,引入积分图的概念[5],将式(2)中的均值μ代入展开得:

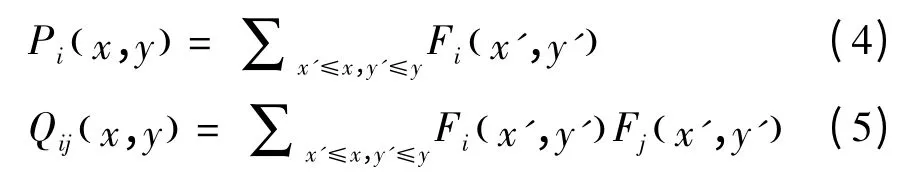
定义向量Px,y和矩阵Qx,y:
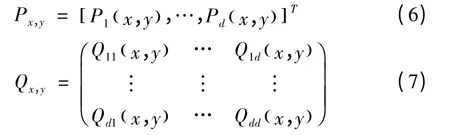
通 过 积 分 图 计 算 Px,y和 Qx,y,则 区 域的表征因子计算如下:

其中,N= ( x″+1 )× ( y″+1 ),经过一系列的变换可以得到区域R( x',y',x″,y″)内的协方差区域描述因子为:
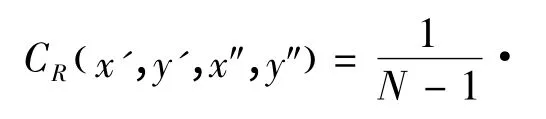
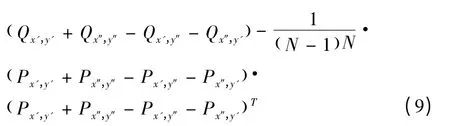
3.2 协方差矩阵之间的度量
两协方差矩阵的相似度用两者之间的距离来度量[6]:
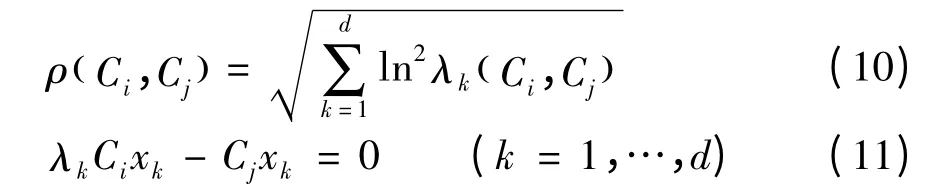
其中,xk为广义特征向量;λk( Ci,Cj)是广义特征值,每个粒子的观测概率定义为:
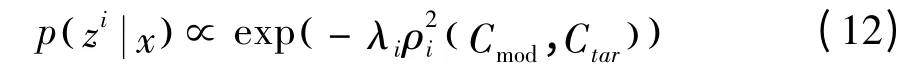
式中,Cmod和Ctar分别为目标模板和每个观测粒子的协方差矩阵。
3.3 算法流程
本文算法实现流程如下:
(1)根据目标初始状态x0,计算协方差矩阵模板C0,令
(2)预测:由xt=Axt-1+W,预测下一帧状态^xt;
(3)在目标状态xt-1周围一定区域内计算每个粒子的协方差矩阵及其观测概率;
(5)计算目标的当前估计状态:珋xt=
(7)转向步骤(2)。
4 仿真试验结果
用目标区域内的每个像素点位置、灰度、一阶导数和二阶导数等9维特征向量得出一个9×9协方差矩阵。为了验证算法的普适性,在数据源的选取上,选择在公共视频集上进行验证,该视频集共773帧,图像的大小为640×480。在同一数据源上,针对同一目标,在人工标定初始位置的前提下,分别进行颜色跟踪、边缘跟踪和本文算法跟踪的仿真。如图2所示,第一行是选择颜色作为目标区域描述子的实验结果,第二行为选择边缘作为目标区域描述子的实验结果,第三行为本文算法跟踪的结果。在第725帧,由于跟踪目标进入阴影区,光线发生较大变化,导致目标的颜色特征发生较大变化,颜色跟踪失效,本文算法和边缘跟踪可以一直跟踪目标。在第758帧,目标受到部分树木的遮挡,背景周围存在较大边缘特征的干扰,导致了边缘跟踪跟丢目标,协方差描述子中除了梯度特征外,还有灰度特征,因此本文算法可以稳定跟踪目标。

图2 试验结果
表1是三种实验结果的对比,由于相似目标、背景边缘等外界因素干扰,单个特征(如颜色、边缘)的跟踪结果往往是不稳定的,通常情况下难以确定哪种特征的跟踪效果更好。协方差矩阵包含目标区域每个像素点的位置信息,当特征的分布产生平移,对协方差矩阵的影响较小,因此该特征对光线变化不敏感。协方差矩阵中除了有目标区域每个像素点的梯度外,还包含了目标的灰度特征,因此对边缘干扰有一定的纠错能力。

表1 试验结果对比
本文中的所有算法均在Intel(R)Core(TM)i7 2.93 GHz 4G内存计算机上用Matlab R2010a仿真实现。本文的三种算法粒子数目均为100,采样点数均为120,表1给出了不同算法的跟踪速度(帧/秒),由表1可知,本文算法的复杂度比颜色跟踪及边缘跟踪的算法复杂度都低,计算效率更高。
5 结论
本文提出了一种基于积分协方差矩阵的粒子滤波目标跟踪,协方差矩阵可融合目标区域的不同特征实现复杂背景下目标的稳定跟踪,利用积分图实现区域协方差快速计算。试验证明本文的跟踪结果较单一特征跟踪结果更稳定,算法的计算复杂度低,计算实时性更好。本文的跟踪算法除了可以在公共安全、视频监控等领域应用外,还可用于视觉导航、视觉导航、自主定位等方面。
[1] HOU Zhiqiang,HAN Chongzhao.A survey of visual tracking[J].Acta Automatica Sinica,2006,32(4):603-617.(in Chinese)侯志强,韩崇昭.视觉跟踪技术综述[J].自动化学报,2006,32(4):603-617.
[2] GU Xin,WANG Haitao,WANG Lingfeng,et al.Fusing multiple features for object tracking based on uncertainty measurement[J].Acta Automatica Sinica,2011,37(5):550-559.(in Chinese)顾鑫,王海涛,汪凌锋,等.基于不确定性度量的多特征融合跟踪[J].自动化学报,2011,37(5):550-559.
[3] F Porikli,O Tuzel,PMeer.Covariance tracking using model update based on lie algebra[J].IEEE Computer Vision and Pattern Recognition,2006,pages:728-735.
[4] LI Shaojun,LI Liren,LIU Zhongling,et al.Terminal guidance target tracking based on region covariance matrix[J].Laser&Infrared,2010,40(3):330-333.(in Chinese)李少军,李立仁,刘忠领,等.基于区域协方差矩阵的末制导目标跟踪[J].激光与红外,2010,40(3):330-333.
[5] F Porikli.Integral histogram:a fast way to extract histograms in cartesian spaces[J].IEEE Conf.on Computer Vision and Pattern Recognition,2005,829-836.
[6] W Forstner,B Moonen.A metric for covariance matrices technical report,dept of geodesy and geoinformatics[J].Stuttgart University,1999.

