基于成像序列的弹道目标ISAR图像横向定标
何兴宇,童宁宁,贺吉峰
(1.空军工程大学防空反导学院,陕西 西安710051;2.驻航天科工集团二院23所军代表室,北京100854)
1 引言
弹道目标特征提取是中段弹道目标识别的基础和关键。弹道目标的特征主要包括微动特征和结构特征,微动特征如进动角、进动周期等,结构特征如尺寸、形状等[1-3]。利用ISAR实现高分辨成像是进行目标结构特征提取的重要途径,而ISAR图像的横向定标是提取目标结构特征的难点和关键。中段弹道目标在转台模型下通常是均匀旋转的,其ISAR图像定标的关键是成像积累角及转速的估计。由于ISAR成像是小角度成像,通常成像积累角不超过10°,依靠单次ISAR像难以完成转速的准确估计[4-6]。
目前,大多数横向定标算法都是基于多特显点法,筛选出包含特显点的距离单元,通过提取这些单元内特显点的回波信号估计调频率。文献[7]通过图像分割划分强散射区域来实现横向定标,该方法利用LPFT(Local Polynomial Fourier Transform,局域多项式傅里叶变换)等算法,实现散射中心的提取和调频斜率的估计,有较高的估计精度,然而图像分割门限确定不准确将直接影响定标精度,算法稳定性不高。文献[7]指出,ISAR图像散射中心相对位置不因目标的三维转动而发生变化,并据此提出了基于图像配准的弹道目标ISAR像横向定标算法,该算法同样需要寻找合适的控制点,通过仿射变换实现ISAR像横向定标。但是该方法敏感于横向伸缩因子的估计,且计算较复杂。本文根据文献[8]分析得到的ISAR图像散射中心相对位置不变的特点,通过提取ISAR图像序列中由散射点构成的模值最大的向量,根据弹道目标的旋转对称性,得到目标对称轴方向的单位向量表示,并估计该向量在成像序列之间的转角及转速,最后完成ISAR像的横向定标。仿真实验表明,本文的ISAR图像定标算法能准确地完成目标转速估计,定标效果较好。
2 ISAR图像定标原理
逆合成孔径雷达利用发射宽带信号达到距离向的高分辨,依靠长的合成孔径实现方位向的高分辨,而距离—多普勒算法是最常用的ISAR成像算法。
雷达工作在线性调频体制下。设目标到雷达的距离为Ri,参考距离为Rref。解调后的雷达回波为[9-11]:
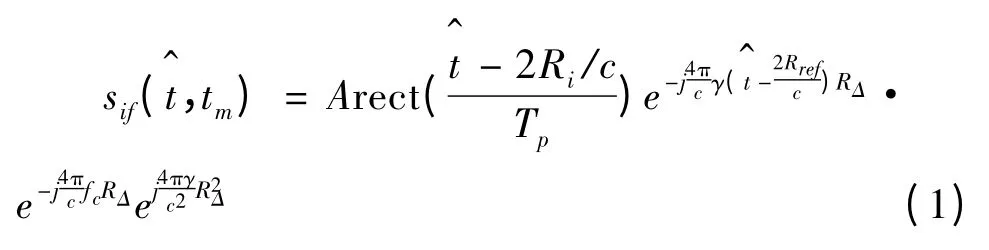
对得到的解调后的回波以fs采样频率进行采样,设每次回波可以得到N个采样点,做Nf点离散傅里叶变换,可得目标的一维距离像:
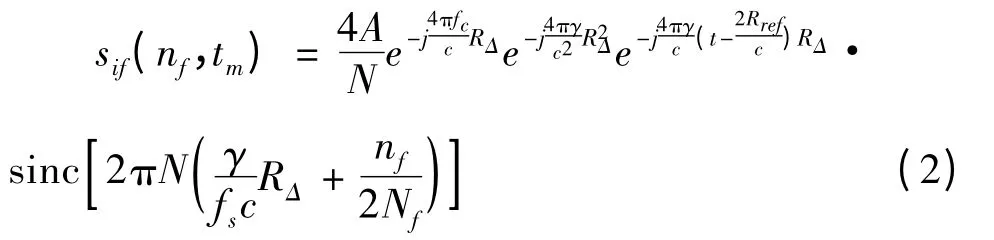
设目标平动补偿后,转动速度为ω,则散射点与参考中心的距离为:
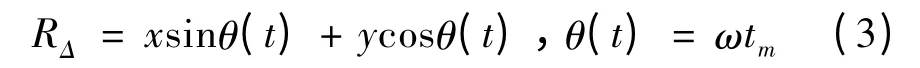
去斜后,在慢时间域作Mf点离散傅里叶变换实现横向压缩,得到目标的ISAR像为:
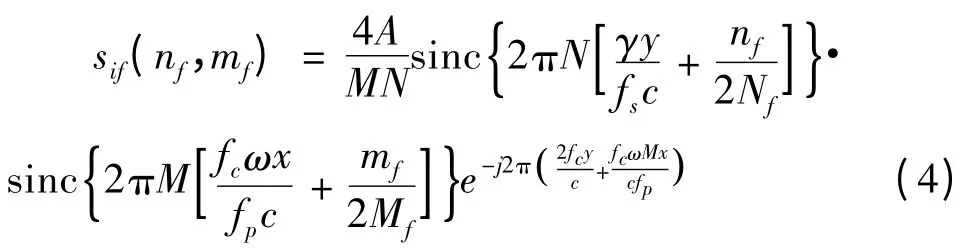
式中,M表示脉冲积累数;fp为脉冲重复频率;(nf,mf)表示尖峰脉冲位置。
由上式可以看出,在完成距离像和横向压缩后,在 ( nf,mf)域会出现sinc函数形式的尖峰脉冲,对应了散射点的位置。尖峰脉冲位置可以用下式表示:

3 转动角速度估计
3.1 模型建立
设ISAR像的纵向分辨率和横向分辨率分别为ρr和ρa,若不发生越距离单元徙动,则目标的最大径向尺寸和横向尺寸应满足以下条件[12]:

式中,λ为雷达发射信号波长;若取λ=4 cm,ρr和ρa均为0.4 m,则目标尺寸应不大于16 m×16 m,弹道目标通常都能满足这一要求,因此本文成像算法中假设散射点不发生越距离单元徙动。
运动目标回波信号经包络对齐和相位补偿,将最终转为转台模型进行成像。假设目标完成平动补偿后,距离变化可以消除,同时,仿真假设识别的弹道目标为锥柱体。
由于ISAR成像是小角度成像,加上干扰噪声等因素的影响,依靠单次ISAR像进行目标转速估计有较大的不确定性。本文提出利用ISAR像序列估计目标转动角速度,对消干扰噪声因素的影响,提高定标精度。其模型如图1所示。
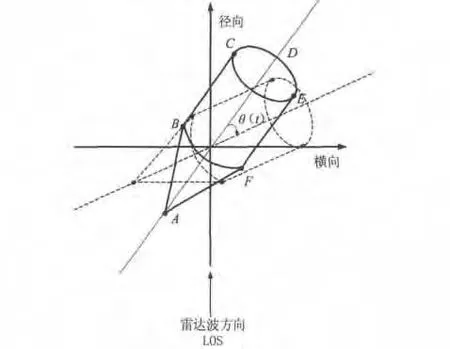
图1 ISAR像序列目标位置及转角
其中,A、B、C、E、F为目标上的五个散射点,AD为目标的对称轴。由目标ISAR像的散射点构成的向量有多个,考察ISAR像中模最大的向量。由于弹道目标的旋转对称性,通常模值最大的向量有两个,可以通过它们来确定对称轴的方向,进而估计成像序列间目标的转角。
3.2 算法分析与设计
假设散射点在ISAR像中坐标分别为(xi,yi),i∈[A,B,C,E,F]。得到各向量的坐标表示,如AB=(xB-xA,yB-yA)。可以看出,向量只与散射点的相对位置有关。
从图1可以看出,模值最大的向量在AC和AE中产生。如果图像聚焦效果不好,将影响向量模值的估计和目标转角的估计精度,进而影响目标的定标精度。因此,对AC和AE向量作以下处理:
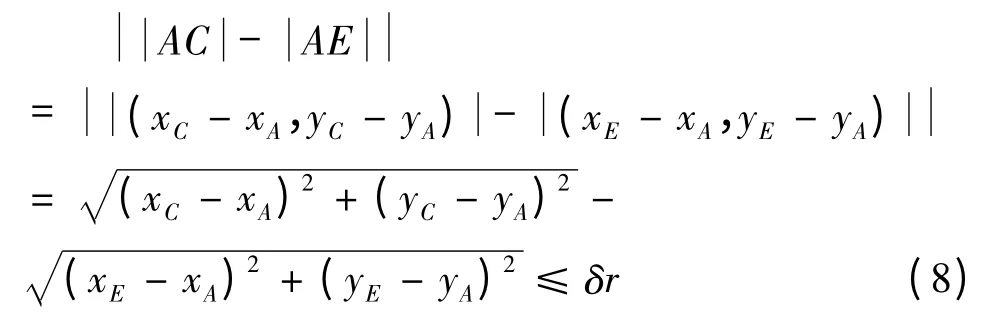
首先,判断式(8)是否成立。式中,δr为允许的偏差值,取δr=1,即两向量的模值差不大于一个横向(径向)距离单元。
当式(8)成立时,判定两向量模值相同,通过计算两向量的合成向量在成像序列中的变化来估计转动角;但是,在目标的一定姿态角下,式(8)并不成立,此时需提取AC和AE中模值大的向量,考察它在成像序列中的变化来估计转动角。本文后面的分析均假设式(8)成立,其他情况可按下面分析作类似处理。
设初始时刻对称轴AD方向的单位向量为e1,则有下式成立:
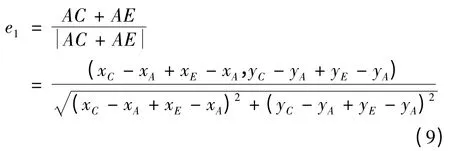
经历时间t后,在下个成像时刻,对称轴方向的单位向量设为e2,则e1与e2的夹角即为在时间t内目标转过的角度θ(t)。有下式成立:
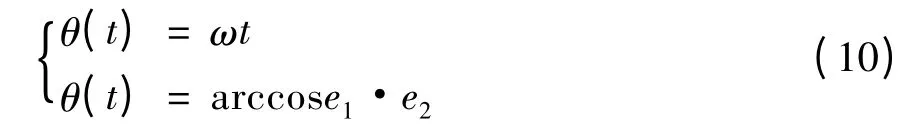
通过式(10),提取目标的转动角,估计目标转速,进而根据式(6)完成目标的横向定标。
4 仿真分析
假设目标由五个散射点组成,其位置关系如图2所示。
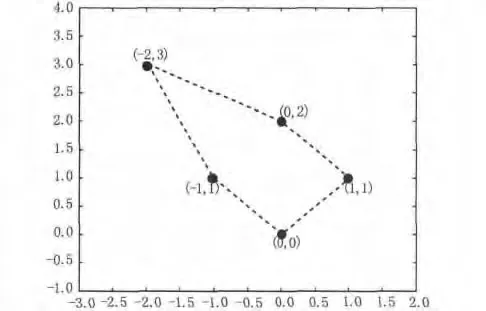
图2 各散射点位置关系
雷达发射的线性调频信号载频fc=6 GHz,波长λ=0.03 m,脉冲宽度Tp=40μs,带宽B=300 MHz,调频斜率k=B/Tp,采样频率Fs=300 MHz。设转台模型逆时针方向旋转为正,转速设置为ω0=0.01 rad/s。
初始成像时刻为t1=0时,根据目标初始时刻的位置,得到目标ISAR像如图3所示。
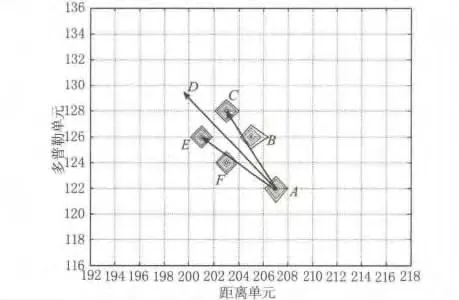
图3 t1=0 s时目标ISAR像
各散射点在ISAR像中的坐标如下:A(207,122),B(205,126),C(203,128),E(201,126),F(203,124)。模值最大的向量为AC=(-4,6)及AE=(-6,4),根据式(9)计算得
二次成像时刻为t2=40 s时,由于转台的转动,各散射点的位置发生了变化,如图4所示。

图4 t2=40 s时目标ISAR像
由t2=40 s时的ISAR像可得AC=(-6,4),AE=(-7,1),=0.14≤1,e2==(-0.9333,0.3590)。
目标在40 s的时间里转过的角度为θ(t)=arccos e1·e2=0.4182 rad,计算得目标转速ω==0.0105 rad/s,与仿真设置的目标转速ω0=0.01 rad/s相当,相对误差=4.5561%,转速估计效果较好。
将得到的转速估计值带入式(6),对t1=0时的ISAR像定标,结果如图5所示。
从图5中的定标结果可以看出,各散射点的相对位置关系与散射点模型基本相同,定标效果较好,精度较高。定标得到的散射点位置与原始模型关于原点对称,这是由于多普勒符号引起的。
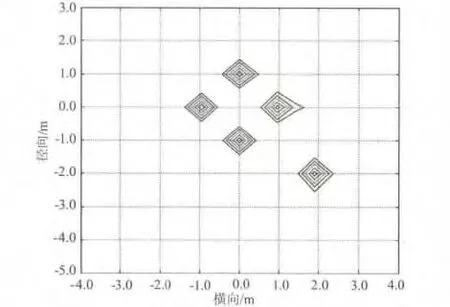
图5 ISAR定标后图像
为了验证算法性能,选取不同的成像序列间隔,得到转角、转速、转速估计误差及横向定标误差如表1所示。
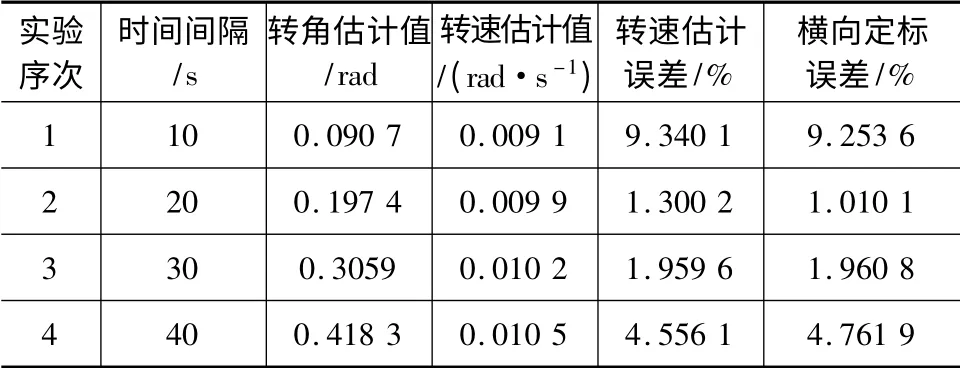
表1 不同序列间隔下的仿真实验结果Tab.1 Simulation results in different time interval
从表1可看出,除了初次实验,转速估计误差和横向定标误差均在5%以下,估计误差较小,横向定标精度较高。从表中还可以看出,在时间间隔较小时,转角及转速估计值误差较高;但是时间间隔的选取也不能过大,否则会由于ISAR像序列中向量相对关系和目标散射特性的变化而导致误差急剧增大。另外,还可以通过选取多个时间间隔来估计目标转速,增加估计和定标精度。
5 结论
弹道目标ISAR图像横向定标在弹道目标识别中有重要地位。本文从经典的距离—多普勒成像算法出发,分析了ISAR成像的特点及利用成像序列估计转速进而完成横向定标的优点。通过对ISAR像序列中散射点构成的向量的分析,得到转角及转速估计表达式,完成弹道目标的横向定标。仿真实验证明了本文方法简单有效,定标精度较高。本文研究了两幅ISAR像实现横向定标的过程,当然还可以通过利用多个ISAR像序列综合来提高定标精度。
[1] Rihaczk A W,Hershkowitz SJ.Theory and practice of radar target identification[M].Boston:Artech House,2000.
[2] Dieter Mehrholz.Radar techniques for the characterization of meter-sized object in space[J].Adv Space Res,2001,28(9):1259-1268.
[3] MA Liang,WANG Tao,FENGDejun,et al.The characteristic of range profile and micro-motion feature extraction for rotary target[J].Acta Electronica Sinica,2008,36(12):2273-2279.(in Chinese)马梁,王涛,冯德军,等.旋转目标距离像长度特性及微运动特征提取[J].电子学报,2008,36(12):2273-2279.
[4] Thayaparan T,Frangos P,Stankovic L.Signal processing techniques for ISAR and feature extraction[J].IET signal processing,2008,2(3):189-191.
[5] JLi,H Ling.Application of adaptive chirplet representation for ISAR feature extraction from target with rotating parts[J].IEE Proc-Radar Sonar Naving,2003,150(4):284-291.
[6]CHEN Xiuwei,ZHANG Yunhua,ZHANG Xiangkun.Ballistic missile echo simulation based on ISAR[J].Journal of Air Force Engineering University:Natural Science Edition,2011,12(1):29-34.(in Chinese)陈秀伟,张云华,张祥坤.弹道导弹的ISAR回波模拟[J].空军工程大学学报:自然科学版,2011,12(1):29-34.
[7] Martorella M.Novel approach for ISAR image crossrange scaling[J].IEEETrans on Aerospace and Electronic Systems,2008,44(1):281-294.
[8] JIN Guanghu,GAO Xunzhang,LI Xiang,et al.ISAR image cross scaling method for ballistic target based on image registration[J].Systems Engineering and Electronics,2010,32(12):2565-2569.(in Chinese)金光虎,高勋章,黎湘,等.基于图像配准的弹道目标ISAR图像横向定标[J].系统工程与电子技术,2010,32(12):2565-2569.
[9] BAO Zheng,XING Mengdao,WANG Tong.Radar imaging technology[M].Beijing:Electronic Industry Press,2005.(in Chinese)保铮,邢孟道,王彤.雷达成像技术[M].北京:电子工业出版社,2005.
[10]QUN Zhang,Tat Soon Yeo,Hwee Siang Tan,et al.Imaging of a moving target with a rotating parts based on the Hough transform[J].IEEE Transactions on Geoscience and Remote Sensing,2008,46(1):291-299.
[11]Jin Guanghu.Research on ISAR imaging and physical feature extraction of midcourse ballistic target[D].Changsha:National University of Defense Technology,2009.(in Chinese)金光虎.中段弹道目标ISAR成像及物理特征反演技术研究[D].长沙:国防科学技术大学,2009.
[12]HU Jiemin,ZHANG Jun,ZHAN Ronghui,et al.Novel method for estimating rotation angle based on phase cancellation[J].Systems Engineering and Electronics,2012,34(5):897-902.(in Chinese)胡杰民,张军,占荣辉,等.一种基于相位对消的转角估计新方法[J].系统工程与电子技术,2012,34(5):897-902.

