改进的单幅红外图像局部自适应非均匀校正
简献忠,陆睿智,郭 强
(1.上海理工大学光电学院 教育部及上海市现代光学系统重点实验室,上海200093;2.国家卫星气象中心,北京100081)
1 引言
目前,红外图像已被广泛应用于工业、医学和军事等领域来进行低可视度下的侦测。然而由于红外探测器具有对空间的非均匀性、对时间的非均匀性以及各敏感元的非线性响应[1],使得成像中包含了呈列分布或行分布(取决于信号的读出方式)的固定图像噪声(FPN)。并且受目前材料和制造工艺等客观条件的限制,成像系统的非均匀性不可避免。这就要求我们用软件的方式来对图像进行校正,使图像得到更好的视觉效果。
常用的红外图像非均匀校正技术主要有定标法和场景法两种。定标法主要有两点校正法、多点校正法等;场景法主要有时域高通滤波法[2]、恒定统计法[3]、神经网络法[4]等。但这两种方法在应用时都有很大的局限性。
文献[5]提出了使用单参数的中值直方图均衡化的校正算法,但通过实验发现在图像的某些局部位置可能会出现校正效果一般甚至丢失部分图像信息等不理想的情况。
针对已有算法的不足,本文利用中值直方图均衡的方法,通过把单幅图像上每一列的信息作用到其他列上,以进行单幅图像的非均匀性校正,然后将图像分为许多分块,令各分块自适应地选择各自最好的校正参数,以达到最优化的校正效果。并且由于只在一幅图像上校正,避免了场景法可能会产生的“鬼影”的干扰问题。
2 算法描述
提出的算法主要包括如下三方面的内容。
2.1 中值直方图简介
大多数基于场景的红外图像校正算法的最终目标都在于均衡各个像素传感器之间的时序直方图。基于这个指导思想,根据文献[5]提出的用于校正不同摄像机间增益差的中值直方图均衡算法,这种算法能够使用不同相机拍摄的图像在均衡其直方图后更方便对比[6],而文献[6]也证明了中值直方图均衡的效果比直接求平均的效果要好。
若两幅图像的累计直方图分别是H1和H2,则其中途累计直方图的计算公式如下:
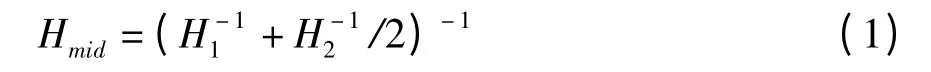
因为图像的单列是包含了足够的用于均衡的信息的,而图像信息是连续的,所以可以认为相邻两列的直方图是近似相等的。换言之,要将每一列的直方图转换为其相邻列的中值直方图。
由于固定图像噪声一般来说并不是孤立的,所以需要将这个方法用在多列图像上,对于各列所占的权重,这里应用高斯权重法进行处理。高斯权重的基本思想是:在分析区每个点上的要素都是由分析区内或某个影响半径内所有要素的加权平均值来确定的,且加权平均的权重值为其间距离的高斯函数值。
2.2 单参数的中值直方图非均匀校正算法
算法的执行步骤描述如下:
1)计算出图像每一列相对于每个像素值l的累计直方图。
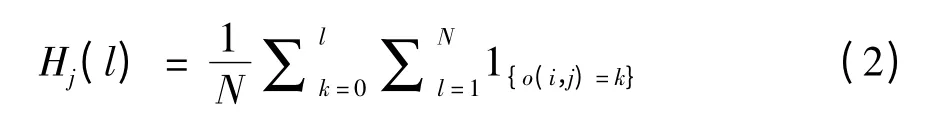
其中,N表示图像的行数,即每一列图像上的像素个数;o(i,j)=k表示图像(i,j)位置的像素值为k。
2)根据已有的累计直方图计算出每一列的中值直方图。
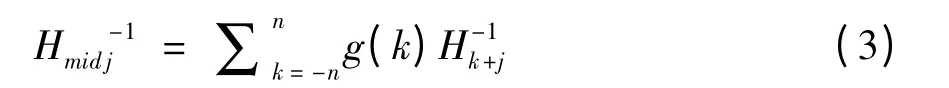
g(k)是高斯权重函数,当校正参数为s时,
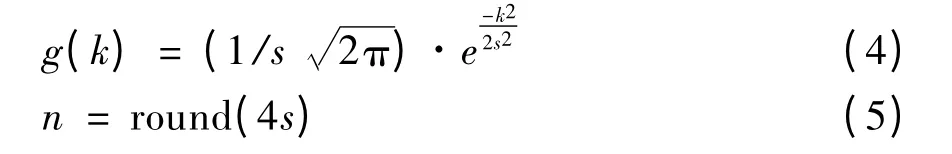
表示将4s向负无穷方向取整;
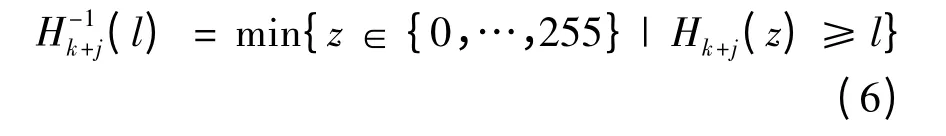
这可以近似理解为累计直方图的逆运算,求出(k+j)列上恰好大于等于累计直方图值l的累计直方图所对应的像素灰度值。
3)计算出对应于校正参数s的每一个点校正后的灰度值:
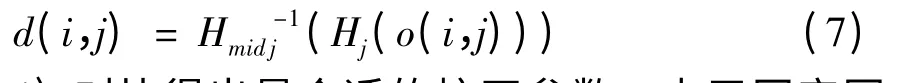
4)对比得出最合适的校正参数。由于固定图像噪声的存在,导致了图像每一行上相邻点之间灰度值的差异较大。所以可以认为使得每一行上,相邻点间差值的绝对值最小的校正参数是最合适的。即该参数s使得公式(8)所求出的值最小。因为正确校正后的图像在视觉效果上会让人感觉比较平滑,即相邻的像素灰度值之间的变化应该比较小。
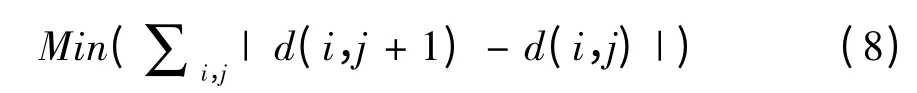
选出作用于全图的最好校正参数后,该参数对应的校正结果就是单参数的校正结果。
2.3 多参数的局部自适应中值直方图非均匀校正算法
从2.2小节中所描述的算法里,我们可以注意到对于不同情况的图像,无法预先知道什么样的校正参数能够使整幅图像达到最好的校正效果,只能在完成校正后再选择出最好的参数。而同一幅图上,不同部位的图像信息肯定存在不容忽视的差异,所以整幅图像都使用同一个校正参数是不合理的。于是可以将图像切割为独立的小块,然后让各小块自适应的选择出各自最合适的校正参数,以达到更好的校正效果。
算法描述如下:
1)先将原图像用所有预设的校正参数s进行处理,把得到的全部结果都保存起来;
2)把所有结果都进行同样的分块处理;
3)对每一个分块都使用公式(8)计算得到各自对应的结果,然后找出这一结果所对应的校正参数;
4)把所有块都处理完成后,将得到的结果按次序合并为完整的图像。
这样我们就使得每一个分块都得到了最好的校正效果。
3 实验及结果分析
采集实验数据的红外焦平面由4个512模块拼接而成,其中左边为中波,右边为短波;短波红外(1.1~3.0)±0.2μm;中波红外(3~4.8)±0.2 μm单个模块奇偶像元沿列方向错开2个像元;中短波原始数据中,辅助数据信息已剥离。原图像的分辨率为1024×768。将图像分块时,本文将其分为256×256的12块。
此算法的仿真在Win7操作系统MATLAB仿真软件中实现。
本次实验校正参数s的设置范围是0.25~20.00,每次递增0.25。
为了客观地评价实验结果,本实验根据文献[7]使用均方误差(RMSE)、根据文献[8]采用峰值信噪比(PSNR)以及每一行上列间差值的绝对值的图像共三个评价指标来对实验结果进行评价。
图1(a)是原始图像,可以明显的看出图像的列上有严重的非均匀噪声,其RMSE值为41.2258,PSNR值为15.8614;图1(b)是使用单参数校正后的结果,最后校正参数s=10.5,其RMSE值为40.1576,相比原图的RMSE值改变了1.0682,PSNR值为16.0895,相比原图的PSNR值改变了0.2281;图1(c)是使用本文提出的局部自适应多参数算法校正后的结果,其RMSE值为40.1178,相比原图的RMSE改变了1.1080,与单参数相比,该标准的改变量赠加了3.72%,PSNR值为16.0981,相比原图的PSNR值改变了0.2367,与单参数相比,该标准的改变量增加了3.77%。

图1 两种算法的结果与原图的对比Fig.1 comparison of results
可以看出,本文提出的算法比文献[5]、[10]提出的全图使用单参数的算法在结果上得到了更进一步的改进;相较于其他校正算法,在结果上,文献[10]也证明了这种方法的校正效果优于TV模算法。
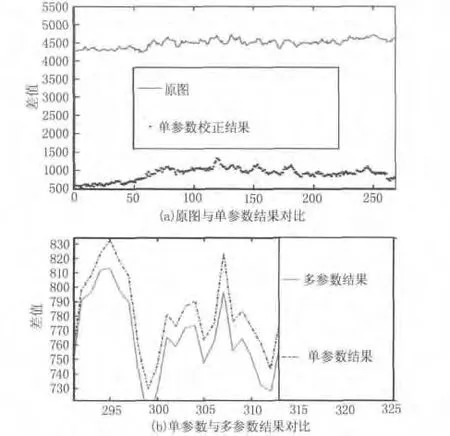
图2 列间差值的绝对值Fig.2 absolute value of difference between columns
图2 是每一行上列间差值绝对值的对比图,该值越小则说明图像灰度跳变越小,即越平滑。图2(a)为原图与单参数结果的对比;图2(b)为单参数结果与多参数结果的对比。
图3是单参数算法和多参数算法的局部对比图,截取了i=860∶980;j=270∶768的部分图像。图3(a)为单参数结果;图3(b)为多参数结果。
但由于红外图像成像系统的原因,导致生成的图像分辨率比较低,不方便进行对比。这里利用photoshop软件对图像进行相同的“亮度/对比度”的预处理,以便更直观地进行比较。可以看出,图3(a)中很多模糊的地方,在图3(b)中都得到了明显的改善;在对比图中上半部分中间位置处,图3(a)中还有很多呈列分布的固定图像噪声,其在图3(b)中也已被消除。对比单参数算法,多参数算法在局部细节上取得了明显的改进,并且在中间位置处明显保留了更多的图像细节。
图3(c)是未进行“亮度/对比度”的预处理前图3(a)与图3(b)的行间差值绝对值的对比图。结果显示:在局部上,提出的算法也使得结果更加的平滑。
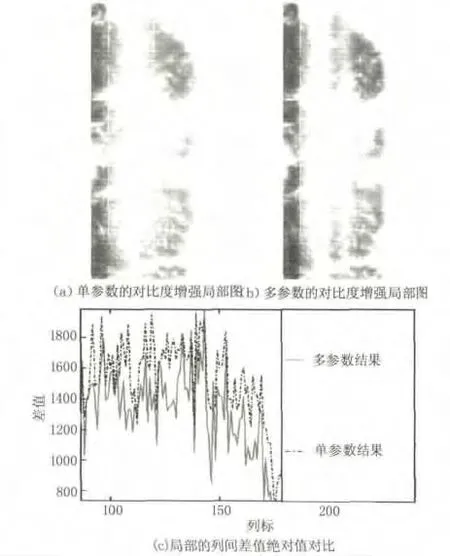
图3 结果的局部对比Fig.3 locally comparison
图4 为另一幅图像的实验结果对比。图4(a)是原图,RMSE值为41.4556,PSNR值为15.8131;图4(b)是单参数算法的处理结果,RMSE值为40.4280,改变量为1.0276,PSNR值为16.0312,改变量为0.2181;图4(c)是多参数算法的处理结果,RMSE值为40.3342,改变量为1.1214,相比单参数,改标准的改变量增加了9.13%,PSNR值为16.0513,改变量为0.2382,相比单参数,该标准的改变量增加了9.22%。

图4 两种算法的结果与原图的对比Fig.4 comparison of results
图5 是图4的单参数与多参数处理结果的行间差值绝对值的对比图。
通过以上实验均可以看出,提出的多参数算法明显比单参数算法得到了更理想的校正效果。
4 结论
本文提出了一种采用基于高斯权重思想的中值直方图非均匀算法实现单幅红外图像的非均匀校正。
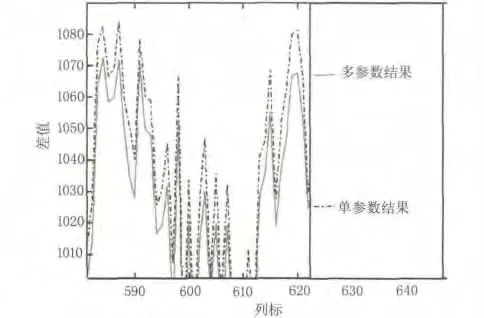
图5 行间差值绝对值对比图Fig.5 absolute value of difference between columns
实验结果证明相对于全图仅使用单个校正参数的中值直方图均衡化算法,提出的新算法使得图像更加平滑,而且在原本校正效果不理想的局部也有了较为明显的改善。另外,提出的新算法保留了更多的图像信息,这对红外图像的诸多应用(红外指纹识别、微小目标识别等方面)有着非常重大的作用。
由于这种方法只在单幅图像上处理,从根本上避免了由于采集系统移动不充分或者场景变换导致的“鬼影”现象,也有效地避免了焦平面探测器元件的参数随时间飘逸的影响。而且该算法由于运算简单,有利于工程实现。
[1] DONG Zhenshi,LIU Xiaobo.The Simplified Math-ematical Model Research for Infrared Focal Plane Arrays Nonuniformity[J].Laser&Infrared,2003,33(3):208-211.(in Chinese)董珍时,刘小波.红外焦平面探测器非均匀性的简化数学模型[J].激光与红外,2003,33(3):208-211.
[2] D Scribner,K Sarkady,M Kruer.Adaptive retina-like preprocessing for imaging detector arrays[J].Proceeding of the IEEE International Conference on Neural Networks,1993,3:1955-1960.
[3] JG Harris,Y M Chiang.Nonuniformity correction using constant statistics constraint:analog and digital implementation[J].Proc.SPIE,1997,3061:895-905.
[4] D Scribner,K Sarkady,M Kruer,et al.Adaptive nonuniformity correction for IR focal plane arrays using neural net-works[C]//Proc.SPIE,1991,1541:100-109.
[5] HE Ming,WANG Yadi,WANG Xinsai,et al.Non-uniformity correc-tion algorithm based on midway histogram equalization in single infrared image[J].Infrared and Laser Engineering,2012,41(9):2550-2553.(in Chinese)贺明,王亚弟,王新赛,等.中值直方图均衡的单帧红外图像非均匀校正算法[J].红外与激光工程,2012,41(9):2550-2553.
[6] Julie Delon,Agnes Desolneu-X.Stabilization of flickerlike effects in image sequences through local contrast correction[J].SIAM Journal on Imaging Sciences,2009,2:6.
[7] SN Torres,M M Hayat.Kalman filtering for adaptive nonuniformity correction in infrared focal plane arrays[J].JOpt Soc Am A,2003,20(3):470-481.
[8] LIU Yongjin,ZHU Hong,ZHAO Yigong.Non-uniformity corruption algorithm based on infrared focal plane array readout architecture[J].Opt.Precision Eng.,2008,16(1):128-134.(in Chinese)刘永进,朱红,赵亦工.基于红外焦平面阵列读出结构的非均匀校正算[J].光学 精密工程,2008,16(1):128-134.
[9] Delon J.Midway image equalization[J].Journal of Mathematical Imaging and Vision,2004,21(2):119-134.
[10]KANG Changqin,ZHANG Qilin,ZHENG Yi,et al.Non uniformity correction algorithm for IR images based on midway equalization histo-gram[J].Laser&Infrared,2013,43(11):1240-1242.(in Chinese)康长青,张其林,郑毅,等.基于中间均衡直方图的红外图像非均匀性校正[J].激光与红外,2013,43(11):1240-1242.

