伺服驱动器散热器的热设计优化

史贤忠，杜佳星，刘缵阁，周武

（武汉迈信电气技术有限公司，湖北武汉430223）

0 引言

随着电子工业技术的发展，电子产品向着大功率密度、高效率的方向发展，以实现轻量化与小型化，各发热元器件发热量也随之增加。而对大多数电子元器件而言，其失效率随温度的升高呈指数增长趋势，据相关文献统计，电子设备的失效有55%［1］是温度过高所引起的。另据统计，对于系统而言，单个电子元器件的温度升高10℃，系统的可靠性降低50%［2］。防止电子元器件的热失效是热控制的主要目标［3］。系统如何对设备内部发热元器件进行散热，保证系统正常运行，已成为设计人员必须要重点解决的关键问题。

采用数值模拟方法已经成为了结构设计人员进行热分析的主要方式之一，该技术不仅能较好地模拟温差作用下气流的流动，而且对温度场的模拟也可以达到较高的精度，这使得设计人员能够通过数值实验的方法方便地进行模型优化，以消除热聚集带来的影响，减少设计、生产、实验的循环次数，大大降低了研发成本［4］。国内外许多公司和单位均采用此类软件帮助新产品进行热设计。如王坚等［5］对电子设备机箱的散热肋数目和尺寸进行了优化；王萌等［6］针对高密度密封电子设备的机箱散热片和芯片到热板的尺寸进行了优化；赵地［7］采用热分析软件对某工作设备进行热分析与设计。

在伺服驱动器中，散热器发挥着散热核心的作用，主发热源均依靠其将绝大部分热量散发到外界热层中去。因此，散热器的优化设计对整个产品的热设计起着至关重要的作用。本研究将结合热动力仿真分析和工程设计经验的技术应用到伺服驱动器散热器优化设计中，通过对比仿真分析的温度场分布图，优选出散热器最佳设计方案。

1 问题描述

在伺服系统控制柜中，伺服驱动器的工作环境温度为0～40℃。其主要发热源包括1个逆变器和2个整流桥，采用散热器自然对流对其进行冷却散热。在保证设备在最高温工况下可靠工作的同时又要降低散热器的重量及加工成本。

2 热传递基本理论

热量的传递有导热、对流换热及辐射换热3种方式。在终端设备散热过程中，这3种方式都有发生。3种传热方式传递的热量分别由以下公式计算：

（1）Fourier导热公式：

（2）Newton对流热换公式：

（3）辐射4次方定律：

式中：λ—导热系数，W/m·K；α—对流换热系数，W/m2·K；ε—表面辐射率；A—换热面积，m2；Q—热量，W；Th，Tc，Tw，Tair—高温面、低温面、固体壁面和流体的温度，℃。

3 热仿真分析

3.1 数值计算理论基础

ICEPAK在处理层流传热问题时，其通过同时计算质量、动量以及能量传递方程这3组控制方程来求解Navier-Stokes方程。处理湍流传热问题时，其在3组控制方程上增加对应的附加方程进行求解，其中零式方程在通常情况下能取得较好的结果。以下是3组控制方程以及零式方程：

（1）质量守恒方程（针对不可压缩流体）：

（2）动量方程：

（3）能量守恒方程：

（4）零式方程：

3.2 建模

根据设计要求，该新型伺服驱动器外形尺寸为L×W×H=200 mm×152 mm×20 mm。其结构形式主要包括一个散热器、两层PCB板、开孔塑料外壳及一个逆变器和两个整流桥，逆变器和整流桥均紧贴着散热器，塑料外壳为半包式，散热器肋片裸露在箱体外部。使用3D软件建立伺服驱动器简化模型，为节约计算资源，箱体内部做了一定简化。省去接线端子、微小发热量的电子元器件等模型，简化模型如图1所示。

图1 伺服驱动器简化3D模型

3.3 设定初始条件及边界条件

流体计算域设定为比箱体模型外围尺寸单边多出50 mm。设置分析类型为内部流动、固体导热，流体介质为空气，计算域边界全部设为Opening，环境温度为20℃。塑料外壳底部为自然对流进风口，侧面为出风口。散热器材料采用Al6063，导热系数λ=209 W/m·K；塑料外壳材料采用ABS，导热系数λ=0.25 W/m·K；PCB材料平面方向导热系数λ=45 W/m·K，垂直方向导热系数λ=0.3 W/m·K；逆变器和整流桥全部采用铜材料代替，导热系数λ=387.6 W/m·K，其热耗如表1所示。

表1 发热元器件特征参数

3.4 仿真分析及优化

仿真分析着重于散热器结构尺寸优化。通过调整散热器基板厚度b、肋片间距l、肋片高度h以及肋片厚度δ等几个关键尺寸来获得仿真分析方案。首先通过矩形肋片优化出较优方案，再在此基础上依据“当材料、热换系数和肋基热流量对肋基过余温度之比相同时，三角形断面重量只有矩形断面的69%”［9］重要结论，结合加工工艺性，适当选取梯形断面方案作为进一步优化方向，提出以下几种优化方案，其中选取某原方案作为优化参考标准。散热器肋片截面结构尺寸示意图如图2所示。

图2 散热器肋片截面结构示意图

（1）方案1：肋片间距l由6.2 mm缩小至5 mm；

（2）方案2：肋片间距l由6.2 mm缩小至4 mm；

（3）方案3：基板厚度b由4 mm增至5 mm；

（4）方案4：在方案3基础上，保证重量不变的情况下，矩形肋片变形为梯形（拟合三角形）肋片，肋片根厚δ由1.5 mm增至2.1 mm，相邻肋片夹角α由0°增至4.6°。

忽略温度升高导致热源热耗大小、热导率变化等非线性因素的影响，主要以热源最高温升作为比较对象。原方案及优化方案1～4散热器与热源温度场分布图分别如图3～7所示。

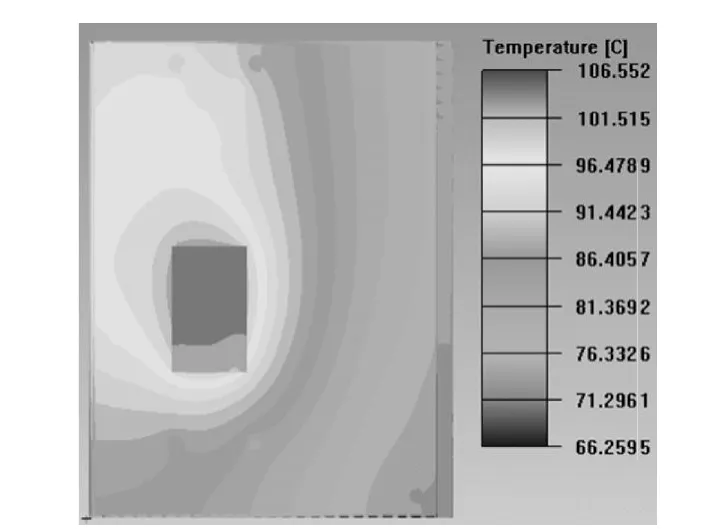
图3 原方案温度场分布

图4 方案1温度场分布图图

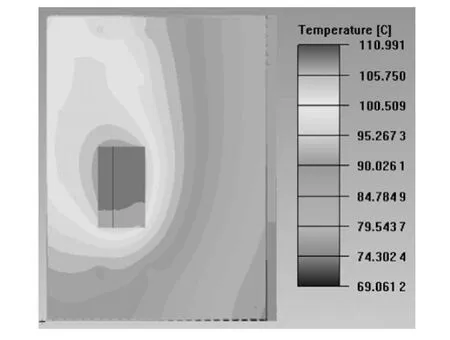
图5 方案2温度场分布图

图6 方案3温度场分布图

图7 方案4温度场分布图

本研究依据上述分析结果，提取各方案热源最高温温升，如表2所示。

表2 各方案肋片结构尺寸与热源最高温温升对照表

3.5 结果分析

（1）对比方案1、2分析结果与原方案可看出，在原方案肋片其他尺寸不变条件下，减小肋片间距、增大散热面积反而使得温升增加、散热条件变差，其主要原因为肋片间距减小后尽管增加一定散热面积，但肋片间空气流动阻力增加，不利于散热。

（2）对比方案3与原方案可知，增加基板厚度、增高肋片高度，使得最高温升从86.5℃降低至81.9℃，效率提高了约5%。

（3）方案4相比方案3，同等体积、重量条件下，增加肋片根部厚度，减小肋片端面厚度，拟合接近三角形肋片，最高温升降低至80.6℃，散热效率提高了约6.8%。

（4）结合表1和表2可知，发热电子元器件的最高工作结温为125℃，而方案4最高温升为80.6℃，结合40℃工作环境温度，120.6℃的最高温小于最高工作结温125℃，满足使用条件要求。

4 结束语

通过仿真分析软件优化出矩形肋片尺寸，再结合“当材料、热换系数和肋基热流量对肋基过余温度之比相同时，三角形断面重量只有矩形断面的69%”重要结论，获得散热效果更优的梯形（拟合三角形）肋片断面设计方案，使得散热效率提高了约6.8%。本研究方法在一定程度上降低了电子元器件温升，提高了产品的可靠性，增加了产品的市场竞争力。

（

）：

［1］刘明安，董秋霞，陈硕.开式机箱电子设备热设计的数值研究［J］.空军工程大学学报：自然科学版，2005，6（2）：62-65.

［2］NELSON L A，SEKHON K S，FRITZ J E.Direct heat pipe cooling of semiconductor devices［C］//Proceeding of the 3th International Heat Pipe Conference，Palo Alto：［s.n.］，1978：373-376.

［3］邱成悌，赵淳殳，蒋全兴.电子设备结构设计原理［M］.修订本.南京：东南大学出版社，2002.

［4］袁亚辉.基于6sigma ET的某电子设备瞬态热设计［J］.机械，2013，40（8）：36-39.

［5］王坚，徐国华.电子设备热分析及优化设计［J］.广东工业大学学报，2003，20（3）：54-63.

［6］王萌，徐晓婷.高密度密封电子设备热设计及结构优化［J］.电子工艺技术，2006，27（6）：339-343.

［7］赵地.嵌入式计算机系统功耗散热分析及优化设计［D］.西安：西安电子科技大学通信工程学院，2007.

［8］Ansys Inc.Icepak User's Guide［CP］.SASIPInc.，2011.

［9］余建祖，高红霞，谢永奇.电子设备热设计及分析技术［M］.2版.北京：高等教育出版社，2001.