基于正弦力加载的力传感器动态标定技术研究

谢伟东，尹浩

（浙江工业大学车辆工程研究所，浙江杭州310014）

0 引言

在航空航天、车辆、舰船、兵器、机器人、材料试验等诸多领域，力电测系统（即以计算机—力传感器为平台的力测量系统）已被广泛使用。力电测系统主要用以担负动态力的测量任务，尤其是拉压双向动态力。但是在力传感器的计量校准方面，长期以来是以“静标动用”的方法进行，即以计量器具静态校准时的数据结果作为动态测试时的依据，误差较大［1-2］。力传感器动态标定要求有精确的动态力发生装置。但是迄今为止，国内外均没有技术成熟、性能可靠和实用的动态标定装置。全国计量系统均无力传感器动态校准能力，除航天、军工等少数部门建立了一定的动态标定装置以外，民用工业领域仍然普遍采用“静标动用”的方法［3-4］。因此对力传感器动态标定的研究意义重大。

从国内外相关研究情况看，力传感器动态标定主要采用瞬变力源和正弦力源两类激励方法，其中正弦力源激励式易于控制，精度及可靠性较高［5-6］。笔者在长期研究正弦激振技术及其工业应用的过程中，发明了一种新型正弦激励装置，其相关成果已在汽车工业领域推广应用［7-8］。

以此为基础，本研究提出一种新型的正弦力加载式力传感器动态标定方法，设计相应装置，搭建标定系统，并进行实验，有望为我国相关领域和计量部门提供一种先进、实用的动态标定技术方案。

1 标定原理

本研究提出的正弦力加载式力传感器动态标定原理如图1所示。

图1 标定原理

工控机控制电机变频器驱动电机以一定频率推动正弦机构运动。其正弦机构的主滑块上连接着待标定的力传感器，力传感器上又刚性连接着负载质量块。同时，正弦机构主滑块上还装有位移传感器以测量其产生正弦波的位移。正弦机构原理如图2所示，根据机械原理可知，当曲柄盘在电机带动下匀速转动时，主滑块与力传感器和负载质量块变做往复正弦运动，根据牛顿第二定律可知，力传感器受到的动态力是正弦力。其幅值可表示为：

式中：mload—负载质量，r—曲柄半径，ω—曲柄角速度。

图2 正弦机构原理

力传感器的输出信号通过信号调理器放大、隔离后被数据采集卡采集并保存在工控机中。经数据处理程序处理后便可求得其输出正弦信号的幅值U。

位移传感器的输出信号同样通过信号调理器、数据采集卡后被保存到工控机中。通过将其输出正弦信号与理论正弦信号的比较，可以计算出该正弦机构产生的正弦力的精度。同时其输出的正弦信号幅值等于正弦机构的曲柄半径，由于该机构的曲柄半径可调，直接测量其值并不方便，利用该方法测量曲柄半径不仅方便且精度也高。将计算得到的曲柄半径代入式（1），即可计算出实际施加给力传感器的正弦力幅值F。

力传感器输出电压U和力传感器理论受力F之比便为力传感器的动态灵敏度。该参数为力传感器最重要的动态参数，其反映了力传感器输出电压与实际受力的关系［9］，也是该标定的求取目标：

通过改变电机转速即可实现对力传感器的扫频标定，求取其在不同频率下的灵敏度，从而完成对力传感器的动态标定。

通过改变负载质量块的质量、曲柄半径即可实现可变力值的动态标定。

1.1 数据处理流程

实际上力传感器的刚度虽然很大，但并非完全刚性［10］。由于标定时力传感器随着整个系统振动，会导致力传感器基部与末端的相对运动，从而引入了附加质量Δm，力传感器的实际受力为：

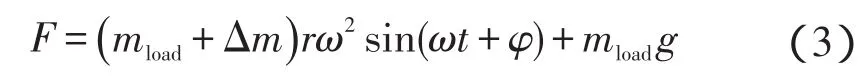
式中：mload—负载质量，r—曲柄半径，ω—曲柄角速度，φ—初始转角。

研究表明，该附加质量与力传感器的具体特性相关，且随频率变化，为了去除附加质量对标定结果的干扰，笔者采用差值法，即在一次标定实验时，分别采用两块质量不同的负载质量块A和B，进行两次实验。根据式（2）和式（3）可得：

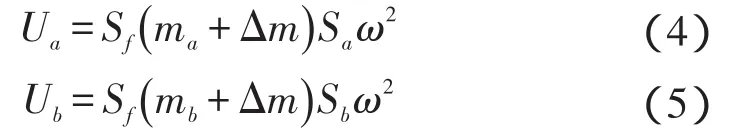
式中：ma，mb—两次实验负载质量块的质量；Ua，Ub—力传感器的输出正弦电压的幅值；Sa，Sb—位移传感器输出的正弦位移的幅值，其数值等于曲柄半径，由于两次实验曲柄半径并未变化故两者相等。

式（4）与式（5）相减并简化后即可得力传感器的动态灵敏度计算式：

位移传感器输出电压S[n]和力传感器输出电压U[n]首先通过低通滤波，去除高频噪音，然后再通过曲线拟合法进行其幅值和相位的计算，最后根据式（6）来求解力传感器的动态灵敏度。其基本流程如图3所示。

图3 数据处理流程

一个标准的正弦信号序列可以表示为：

根据和角公式，式（6）可变为：

令a0=acosφ，a1=asinφ，a2=b，则有：

a0、a1、a2可根据最小二乘拟合法计算，首先定义：

定义数据矩阵为A，系数矩阵为x，输出信号矩阵为b，则有：

将式（9）写成线性方程组形式：

通过计算该方程组的最小二乘解，便可求得a0、a1、a2。

之后正弦信号的幅值、相位即可根据下式进行计算：

将求得的幅值代入式（6），即可算出待标定力传感器的动态灵敏度。

以上述原理为基础，本研究在LabVIEW中设计了相应数据处理程序，其主界面如图4所示。

图4 数据处理程序主界面

通过输入两个负载质量块质量和位移传感器的灵敏度后，系统会自动求解实际标定频率、力传感器的动态灵敏度以及输入、输出的相位差。

2 实验

为了验证该标定系统的可行性，本研究进行了实验验证。笔者搭建的实验平台如图5所示。

图5 实验平台

该标定实验对Interface公司的1010AJ型力传感器及其适配的放大器一起进行了1 Hz～5 Hz的扫频标定，标定结果如表1所示。笔者绘制的动态灵敏度曲线如图6所示。

本研究事先通过静态标定实验，得到该传感器的静态灵敏度为0.001 723 29 V/N。对比实验数据，可以看到该力传感器在1 Hz～5 Hz的动态灵敏度与静态灵敏度偏差在1%左右。从动态灵敏度曲线可以看到其灵敏度随着频率升高而缓慢变大。由此可以看出：力传感器的动态特性与静态特性有一定差异，以往“静标动用”的方法会产生一定的误差，同时也体现了动态标定的必要性和重要性。

表1 实验数据表

图6 动态灵敏度曲线

4 Hz标定实验时，位移传感器输出信号与理论正弦曲线拟合的结果如图7所示，可以看到正弦机构产生的位移曲线与理论正弦曲线的均方差仅为5.84×10-4。通过对各个频率下的位移传感器输出信号进行拟合，可以得到其最大误差为1%。由此可见该标定系统的正弦力激励精度较高。

图7 位移传感器输出信号与理论正弦曲线拟合结果

3 结束语

本研究提出的基于正弦力加载的力传感器动态标定方法得到了实验验证，笔者通过标定实验求取了Interface 1010AJ型力传感器在各个频率下的灵敏度值，并绘制了动态灵敏度曲线。实验结果表明，该力传感器在动态使用时，其灵敏度会随频率升高而升高，由此可见当涉及动态测量时，对力传感器的动态标定显得十分重要。

该标定系统的主要误差来源于正弦机构发生的正弦力精度，根据对位移传感器输出信号与理论正弦曲线的拟合可以得到，该正弦机构发生的正弦力与理论正弦力的最大误差在1%左右，考虑到负载质量误差、A/D转换误差等其他误差因素，该标定系统的总体误差在1.5%内，精度较高。

在下一阶段，本研究将继续改进实验装置，并进一步改进数据处理系统以减少误差。同时，进一步提高标定频率，实现对力传感器更高频率的标定。

（

）：

［1］张于北.从实验看力传感器动态标定的必要性［J］.测试技术学报，1994，8（2）：65-68.

［2］SCHLEGEL C，KIECKENAP G，GLOCKNER B，et al.Traceable periodic force calibration［J］.Metrologia，2012，49（3）：224-235.

［3］何闻.标准动态力发生装置国内外研究现状［J］.机电工程，1999，6（2）：47-49.

［4］FUJII Y.Toward dynamic force calibration［J］.Measurement，2009，42（7）：1039-1044.

［5］顾宝栋，陈怀海，申凡.力传感器动态标定及其精度分析研究［J］.振动与冲击，2005，24（2）：95-98.

［6］FUJII Y.Proposal for a step response evaluation method for force transducers［J］.Meas.Sci.Technol.，2003（14）：1741-1746.

［7］谢伟东，王磊，汪立明.滚动摩擦正弦机构［P］.中国：ZL2006100503311，2008-10-29.

［8］谢伟东.采用正弦传动装置的车辆减振器试验台［P］.中国：ZL201010122290.9，2011-11-09.

［9］强锡富.传感器［M］.3版.北京：机械工业出版社，2005.

［10］布歇.冲击与振动传感器校准［M］.北京：计量出版社，1984：145-149.