辐射场多极展开的新方法
崔明
(淮阴工学院人事处,江苏淮安223003)
0 引言
电磁辐射是电磁理论的重要内容,在研究辐射场的基本问题[1-8]时几乎均是采用势函数(→A,φ)的方法,文[9-13]从不同侧面指出势函数方法中各种处理技术的不足.另外,文[14]中曾用并矢法直接求解时谐辐射场,给出了直接的场矢量计算公式,在此基础上,文[15]给出直接用场矢量进行全函数的多极展开技术.本文延续这一工作,仿效势函数方法中多极展开的线路,给出辐射场多极展开的新方法与结果.
1 理论公式

由时谐(e-iωt)麦克斯韦方程组及真空物态方程→D=ε0=μ0,可以得到电场矢量(→r)所满足的非齐次亥姆霍兹方程为

对于式(1)外向波的并矢格林函数为[2,14]


基于式(3)的场矢量积分解,研究小区域中时变电磁辐射源在远区激发的辐射场,选取坐标原点在电流分布区域,以r表示由坐标原点到场点的距离,近似有


将式(4)代入式(5),有



则可将式(7)写为
城轨交通的快速发展,数据信息呈J型趋势增长,先前单位的档案管理模式已无法满足日益增加的数据量,大部分单位都在探索新时代下档案管理办法。单位人事档案管理直接影响到单位的企业形象和单位的发展方向。单位领导们也开始注重各部门的档案管理办法基础作用,[1]加强人事档案管理人员的培训和职业操守。档案管理中基层的材料收集工作十分重要,如要做好必须要有扎实的基本功。为了快速解决目前所面临的问题,文中设计了几种信息化时代该如何快速实现档案管理的办法。[2]

2 结果分析
考察式(9)中展开的第一项



该结果代表熟知的电偶极辐射场[1].
对于式(9)中展开的第二项

考察其中的被积函数,结合式(8),改写如下


其中,相应的磁偶极矩、电四极矩分别定义为
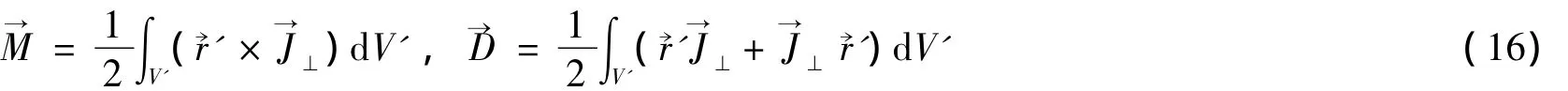
可见,式(15)中的两项分别对应于磁偶极辐射和电四极辐射场.
对于式(9)中的第三项

仿效式(14),可将式(17)中带权重(→r'·→er)的T→⊥被积函数进一步改写.注意利用式(8)和并矢表示,有

代入式(17),给出

定义二阶张量和三阶张量分别为


可见,式(21)中的两项分别代表磁四极辐射和电八极辐射场.
3 讨论与结语
本文借助于场矢量的积分关系,沿用对推迟势的处理方法,给出辐射场矢量多极展开的过程与结果.需要指出:
1)本文采用不同路径所得到的前三项结果与文[15]相一致,表明其处理过程是合适的.
2)虽然所给各阶极矩的定义与通常形式有别,但经检验其给出的场关系是一致的,并且与现有文献相比较,本文的表达更显简明和具有规律性.
3)对于远区辐射场,在保持场矢量大小正比于1/r的前提下,由式(3)自然地过渡到式(5),而不像势函数方法中求得矢势→A后确定场矢量时采用∇→ik→er的代换那么勉强.
4)根据式(9)各项展开的规律特点,比较由式(14)、式(18)等的处理技术,可以效仿地研究更高阶的展开项内容,不难给出更高阶展开式的表示,而文[15]只能给出电偶极、磁偶极与电四极、磁四极与电八极辐射场等三项的结果,在这一点上本文与文[15]不同,本文展开式可以有无限多项.
5)本文结果对于需要更高阶极矩展开结果的场合是有用的,例如原子核与外场相互作用能级的超精细结构中需要考虑原子核的高阶极矩表示等[16],现有文献很少提供高阶极矩展开的结果.文中对于辐射场每项所代表的物理意义进行了分析探讨,对于研究辐射场的多极展开及其应用具有一定意义.
[1] 郭硕鸿.电动力学[M].3版.北京:高等教育出版社,2008.
[2] Kong J A.Theory of Electromagnetic Waves[M].New York:John Wiley&Sons Inc,1975.
[3] Jackson J D.Classical Electrodynamics[M].3ed.New York:John Wiley&Sons Inc,2001.
[4] 戴振铎,鲁述.电磁理论中的并矢格林函数[M].武汉:武汉大学出版社,1995.
[5] 张克潜,李德杰.微波与光电子学中的电磁理论[M].北京:电子工业出版社,2001.
[6] 杨儒贵.高等电磁理论[M].北京:高等教育出版社,2009.
[7] 陈惠青.电磁波理论——无坐标方法[M].梁昌洪,译.北京:电子工业出版社,1988.
[8] 崔元顺.d’Alembert方程的含时Green函数和推迟势[J].大学物理,2002,21(2):12-14.
[9] 高敏树.推迟势幂级数展开的正确方法[J].四川师范大学学报:自然科学版,1999,22(4):450-452.
[10] 刘健平.电势多极展开的一种导出方法[J].西南师范大学学报:自然科学版,2010,35(6):185-189.
[11] 梁昌洪,陈曦.电荷多极子和电流多极子[J].电气电子教学学报,2011,33(4):1-5.
[12] 陈文鑫.电磁辐射的推导及评论[J].乐山师范学院学报,2004,19(5):20-22.
[13] 张福恒.电偶极辐射场计算式的推导[J].海南师范学院学报:自然科学版,2002,15(2):21-24.
[14] 崔元顺.用并矢法直接求解时谐辐射场[J].大学物理,1996,15(12):13-15.
[15] 崔元顺,刘洪香,李建华,等.计算电磁场多极展开的直接方法[J].大学物理,2013,32(10):17-20.
[16] 张春早,武奇.电四极矩及其在原子核物理中的应用研究[J].安徽师范大学学报:自然科学版,2010,33(3):247-249.

