基于椭圆基元光子晶体的宽角度自准直传输研究
孙慧玲, 陈宝锭, 陈华宝, 李清波
(1.淮阴师范学院 人事处, 江苏 淮安 223300; 2.淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)
基于椭圆基元光子晶体的宽角度自准直传输研究
孙慧玲1, 陈宝锭2, 陈华宝2, 李清波2
(1.淮阴师范学院 人事处, 江苏 淮安 223300; 2.淮阴师范学院 物理与电子电气工程学院, 江苏 淮安 223300)
针对二维光子晶体在自准直传输现象,推导了非正交坐标系下的时域有限差分(FDTD)模型,有效地计算了二维椭圆基元光子晶体带隙结构.结合等频图分析,从理论上研究了二维椭圆基元光子晶体结构中TM模式的自准直现象,优化设计出宽角度自准直效应模型,并通过高斯波束验证了其无衍射自导传输模式.
光子晶体; 自准直; 非正交时域有限差分方法
0 引言
自1987年美国贝尔通信实验室的Eli Yablonovitch 教授和美国Priceton大学的Sajeev John教授在Physical Review Letters杂志上独立地提出了光子晶体(Photonic crystals, PCs)的概念以来,光子晶体独特的能带结构以及由此导致的奇特电磁特性使其成为近几十年来一直备受关注的热点研究课题.光子晶体最大的特点就是对光子传播的调控,有关带隙及其应用的研究一直处于光子晶体研究的核心地位,例如:波导[1],滤波器[2],谐振腔[3]等.除了最基本的禁带性质,人们发现通过引入缺陷等方式破坏光子晶体的完整周期后,将在其带隙中形成一些新的模式,例如点缺陷引发的局域共振模式[4],线缺陷产生的波导模式[5].此外,热门的研究还包括光波在光子晶体中传播的动力学效应,包括遂穿,超光速等[6,7].同时,近年来,越来越多的人关注于光子晶体异常色散特性,如负折射,慢光,自准直[8,9].光子晶体中的自准直现象提供一种新的无衍射控制光传播的方式,因而产生了很多新的应用,如虚拟波导[10], 干涉仪[11],光学开光[12],光子内部连接器[13]等.
在光子晶体光子带隙的计算中,最小的计算区域为晶体的一个元胞,传统直角坐标系FDTD的计算网格为矩形,研究非矩形结构的光子晶体时,需要采用超元胞的方法,会引入重复的计算区域.在非正交的情况下,需要选用非正交直线坐标系,只要求计算网格为是非正交的平行四边形,这样就无须采用超元胞的方法,能够简化计算.
本文首先研究了非正交FDTD(the finite-difference time-domain method)的递推公式及光子晶体能带的计算,然后通过光子晶体能带及其等频图优化设计了基于椭圆基元的二维光子晶体实现宽角度自准直模型,理论认为入射角度可以达到±90°范围.
1 非正交坐标FDTD方法
任意斜角的非正交二维坐标系如图1所示.其中直线坐标轴为α,β,z,坐标轴夹角为θ,坐标α,β,z与正交直角坐标x,y有如下关系:
x=α+βcosθ,y=βsinθ,z=z
(1)

图1 任意斜角的非正交二维坐标系
斜坐标系下的协变基矢量为:
(2)
椭圆介质柱中心间距为a,晶格点位置为
Rm,n=(m+ncosθ)aex+(ncosθ)aey
(3)
式中m,n为正整数.倒格子基矢量为:
(4)
(5)
倒格子矢量为:
G=r1b1+r2b2
(6)
其中,r1和r2为整数.

(7)

(8)
(9)
(10)
以及TM波
(11)
(12)
(13)
根据Faraday定理,对TM波方程进行空间离散:
(14)
(15)
(16)
类似,可以得到空间离散的TE波方程.
2 分析及模拟
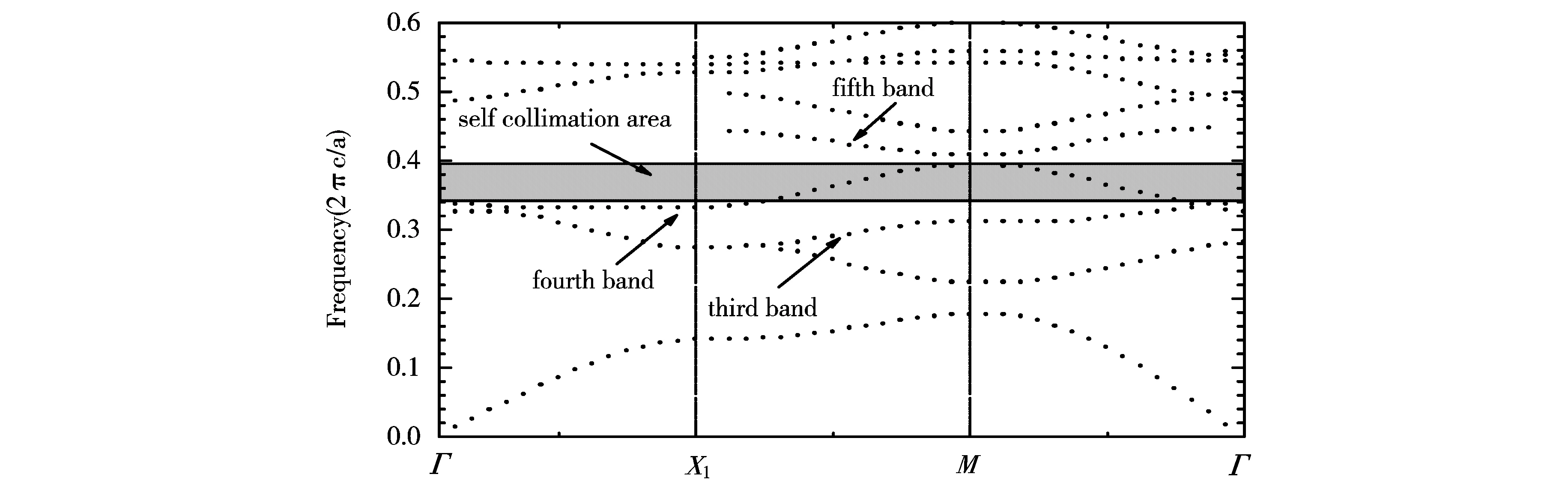
图2 二维光子晶体带隙结构
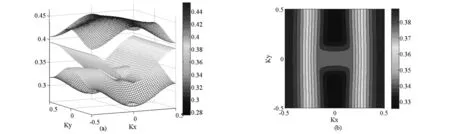
(a)三维等频图 (b)第四条能带的二维等频图
考虑以空气为背景的θ=90°即正方点阵介质型光子晶体.椭圆介质基元的长轴、短轴分别为9 mm,4.4 mm,晶格常数a=10 mm,相对介电常数为21.在本文的研究中,主要考虑电场平行于介质柱的TM模式.为了找到光子晶体中自准直效应出现的频率和传播方向,首先使用非正交FDTD方法计算得到其TM模下的能带结构.TM模式的光子能带结构如图2所示,可见,在第4条能带ΓX1方向存在长距离的平带,在X1M方向,存在线性变化的能带.由于电磁波在光子晶体中的传输方向与其群速度方向保持一致,而群速度vg=kω(k),其中k表示波矢.在波矢空间中,群速度方向与该点处角频率ω(k)的梯度方向一致.所以我们可以初步认为在第4条能带中存在自准直传输现象为了进一步确认,我们利用COMSOL计算了第1、2、5条的三维能带图,如图3a所示.同时,给出了第4条能带的二维等频图,如图3b所示.可以看出,TM模在频率0.34~0.39(2.πc/a)时,等频线的形状接近于直线,其方向垂直于kx,根据自准直效应,在该频率区间电磁波可以在光子晶体内无展宽自准直传输.并且沿ΓX1方向近乎直线的等频线穿过了整个第一布里渊区,理论上对于±90°范围内的入射电磁波都可以产生自准直传输现象.
在距离光子晶体左侧 10a处放置一个沿竖直方向长度为 6a,中心频率为0.363c/a的 TM模高斯线光源,从左侧入射到光子晶体上.使用 COMSOL模拟高斯波束在光子晶体中的传输.图4a和图4b分别仿真在空气背景与椭圆介质光子晶体中的电场分布情况.由图4a可以发现高斯波束在空气背景中的宽度随着传输距离的增加而增大,从而变得发散.当高斯波束入射到光子晶体上时(如图4b),大部分能量被耦合进光子晶体,只有较少的反射,耦合效果很好.耦合到光子晶体中的波束,受自准直效应的约束,即沿电磁波垂直方向的分量为零,沿水平方向无衍射直线传输,并从光子晶体右侧出射.图4c与图4d分别仿真在高斯波束以30°、45°入射到介质光子晶体中的电场分布情况.我们可以发现无论是30°还是45°入射,在光子晶体中都是无衍射水平传输的,波束并没有分散开来,并且波束在右侧出射时的角度依然保持了入射时同样的角度.

图4 沿着kx方向传播高斯波束的电场分布模式
3 结论
光子晶体中的自准直传输提供一种新的无衍射控制电磁波传播的方式,为了找到光子晶体中自准直效应出现的频率和传播方向,本文推导了非正交坐标系下的时域有限差分方法,计算了二维椭圆基元光子晶体TM模下的带隙结构.进而结合等频图分析,从理论上研究了二维光子晶体结构中TM模式的无衍射传输自准直传输模式.此自准直效应模型入射角理论可达到±90°宽角度,无论高斯波束以什么样的角度入射,在光子晶体中都是无衍射传输的,波束不会分散开来,并且波束在出射出光子晶体时的角度依然保持了入射时同样的角度.
[1] Lavrinenko A, Borel P I, Frandsen L H,et al. Comprehensive FDTD modelling of photonic crystal waveguide compon-ents[J].Opt Express, 2004,12(2):234--248.
[2] Notomi M, Shinya A, Mitsugi S, et al.Waveguides, resonators and their coupled elements in photonic crystal slabs[J]. Opt Express,2004,12(8):1551-1561.
[3] Takano H, Akahane Y, Asano T,et al. In-plane-type channel drop filter in a two-dimensional photonic crystal slab[J]. Appl Phys Lett,2004,84(13): 2226-2232.
[4] Tanabe T, Shinya A, Kuramochi E, Kondo S,et al.Single point defect photonic crystal nanocavity with ultrahigh quality factor achieved by using hexapole mode[J]. Applied Physics Letters,2007,91: 021110.
[5] Sugitatsu A, Asano T, Noda S. Characterization of line-defect-waveguide lasers in two-dimensional photonic-crystal sla-bs[J].Applied Physics Letters, 2004,84: 5395.
[6] Ghulinyan M, Oton C J, Gaburro Z, et al. Zener tunneling of light waves in an optical superlattice[J]. Physical Review Letters, 2005,94:127401.
[7] Guan G, Jiang H, Li H,et al.Tunneling modes of photonic heterostructures consisting of single-negative materials[J].Applied Physics Letters,2006, 88(21):211112.
[8] Parimi P V, Lu W T, Vodo P,et al.Negative refraction and left-handed electromagnetism in microwave photonic cryst-als[J].Phys Rev Lett, 2004,92(12):127401.
[9] Kosaka H, Kawashima T, Tomita A, et al. Self-collimating phenomena in photonic crystals[J]. Appl Phys Lett,1999,74:1212.
[10] Gao D S, Zhou Z P, and Citrin D S. Self-collimated waveguide bends and partial bandgap reflection of photonic crystals with parallelogram lattice[J].J Opt Soc Am A,2008,25(3):791-795.
[11] Nguyen H M, Dundar M A, Vander Heijden R W,et al.Compact Mach-Zehnder interferometer based on self-collimation of light in a silicon photonic crystal[J].Opt Express,2010, 18(7):6437-6446.
[12] Zhang Y,Li B.Optical switches and logic gates based on self-collimated beams in two-dimensional photonic crystals[J].Opt Express, 2007,15(15):9287-9292.
[13] Prather D W, Shi S Y, Murakowski J, et al.Self-collimation in photonic crystal structures: a new paradigm for applications and device development[J]. J Phys D: Appl Phys,2007,40:2635-2651.
[责任编辑:李春红]
All-angle Self-collimation in Photonic Crystals with Elliptical Basis
SUN Hui-ling1, CHEN Bao-ding2, CHEN Hua-bao2, LI Qing-bo2
(1.Department of Personnel, Huaiyin Normal University, Huaian Jiangsu 223300, China) (2.School of Physics and Electronic Electrical Engineering, Huaiyin Normal University, Huaian Jiangsu 223300, China)
In view of the self-collimation transmission phenomenon,a finite-difference time-domain scheme in a nonorthogonal coordinate system is presented to calculate the band structure of a two-dimensional photonic crystal.Self-collimation of photonic crystals in the whole angular range of ±90°in the fourth band of a two-dimensional photonic crystals with elliptical basis is demonstrated by examining the band structure and equifrequency contours. non-diffraction guiding modes is verified by a gaussian beam.
photonic crystal; self-collimation; nonorthogonal finite difference time domain method
2013-11-12
江苏省高校大学生创新创业训练计划项目(201310323009Z); 淮安市科技支撑计划项目(HAG2010068)
孙慧玲(1981-), 女, 江苏淮安人, 助理研究员, 硕士, 研究方向为电磁场理论.E-mail: 109884915@qq.com
O413.1
A
1671-6876(2014)02-0121-05

