用于飞机装配的机构运动学与奇异分析
王 杰,张 霖,田 威
(南京航空航天大学机电学院,江苏 南京,210016)
采用数字化自动钻铆装备实现飞机大型构件的装配和联接是提高装配效率和质量的有效途径,也是航空制造业的重要发展趋势[1-2]。在飞机自动化装配系统中,要求系统绝对定位精度为±0.5 mm,重复定位精度为±0.15 mm。已有的自动化钻铆装备多采用“C”型布局机床和关节型机器人自动化装配系统。“C”型机床精度高、刚性好,但体积庞大、成本高且相对工作空间小[3-4];关节型机器人具有结构简单、工作空间大、操作灵活等优点,但刚度和精度低,难以满足钛合金、复合材料等难加工材料的高效、高质量加工[5-6]。因此,迫切需要有另外一种机构形式的机器人以供选择。与串联结构相比,并联结构具有刚度大、精度高等优点,但其灵活度差、工作空间小。由并联结构和串联结构组成的混联机器人,具有结构简单、工作空间大、刚度高和动态性能好等优点[7],其中最有代表性的有Tricept机器人和Exchon机器人[8-10]。以Tricept机器人为例,其精度是一般工业机器人精度的10倍,位置精度能达到±0.2mm,重复定位精度能达到±0.02 mm。因此,混联机器人越来越受到飞机制造商的关注,国外航空企业已开始运用混联机器人作为飞机自动化装配系统。
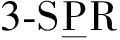
1 自由度分析
1.1 机构模型及坐标系的建立
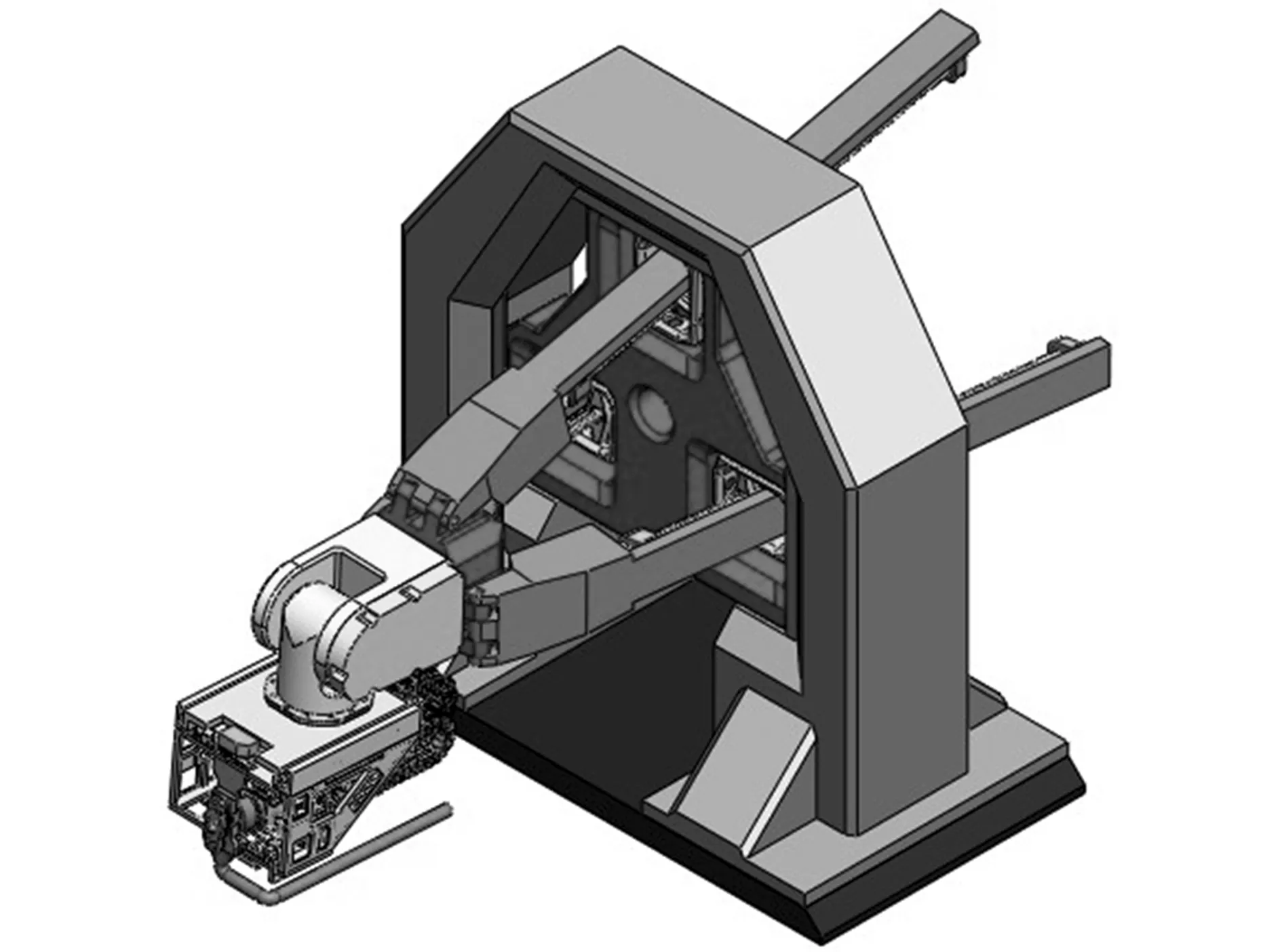
图并联机构模型
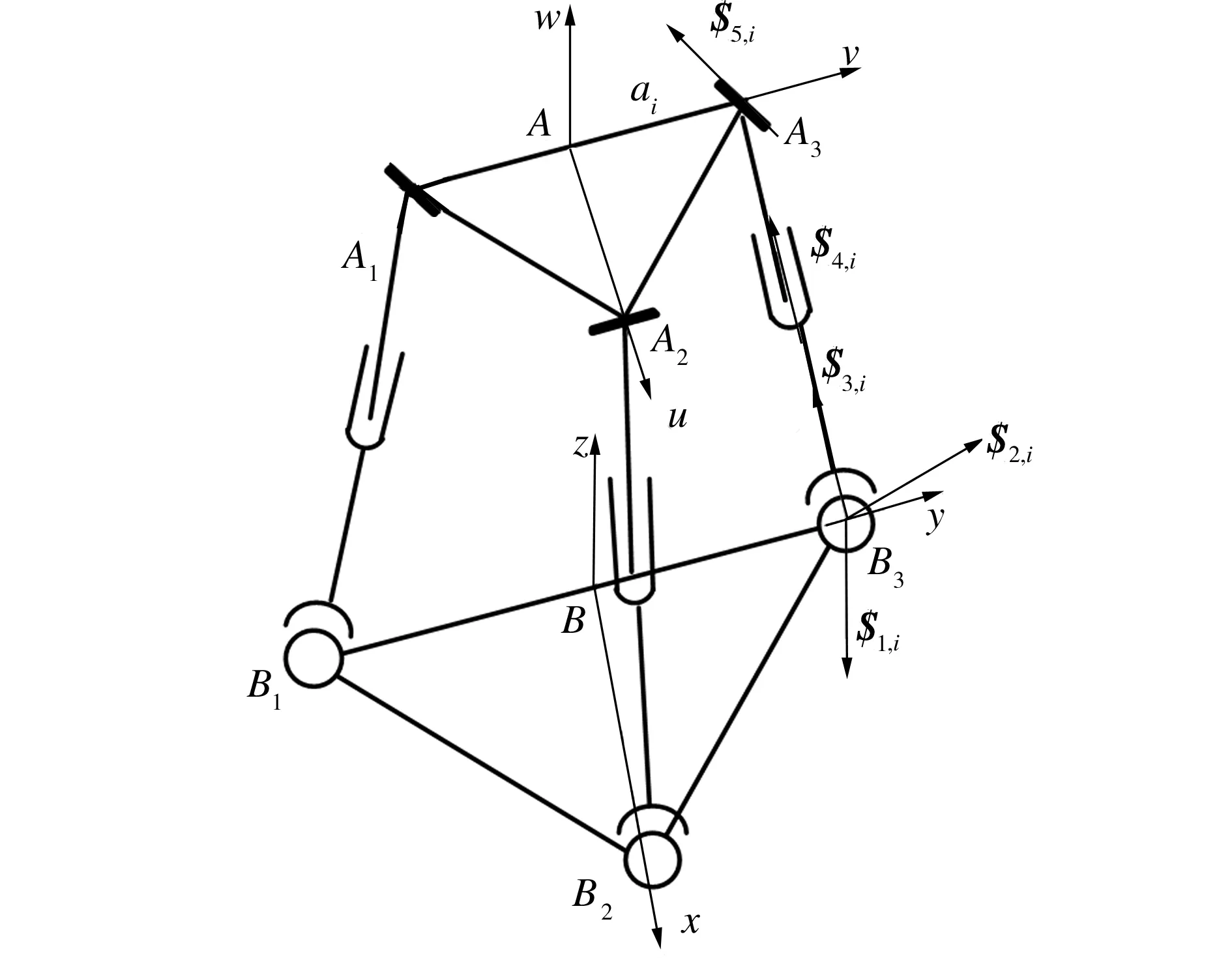
图并联机构结构简图
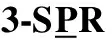
1.2 自由度分析
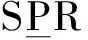
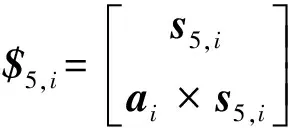
(1)
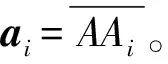
(2)
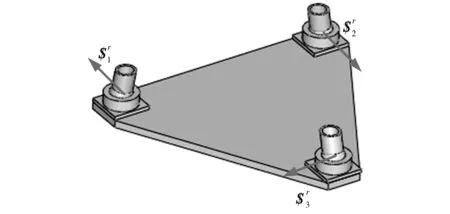
图3 动平台所受约束力螺旋
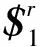
2 位置逆解分析
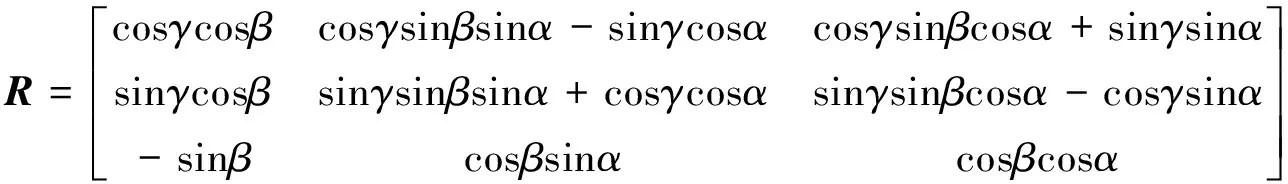
(3)
根据图2可构造闭环约束方程:
r=bi+Lis4,i-ai(i=1,2,3)
(4)
其中,
ai=Rai0;
注意到支链i中转动副轴线s5,i与ai及s4,i存在相互垂直的几何关系,故可构造如下约束方程:
(5)
其中,
s5,i=Rs5,i0;
将式(5)展开并整理可得:
sinγcosβ=0
(6)
xcosγcosβ-zsinβ=0
(7)
(x-b)(cosγsinβsinα-sinγcosα)+
y(sinγsinβsinα+cosγcosα)+
zcosβsinα=0
(8)
对式(6),考虑到β为机构的一个独立自由度,故有γ=0,于是式(7)和式(8)可简化为
xcosβ-zsinβ=0
(9)
(x-b)sinαsinβ+ycosα+zcosβsinα=0
(10)
综上分析可知,给定动平台中心点A的位置坐标(x,y,z)T便可计算出α、β、γ,进而得到选择矩阵R。于是各驱动支链的长度便可通过下式求出:
Li=‖r-bi-Rai0‖(i=1,2,3)
(11)
3 雅克比矩阵分析
(12)
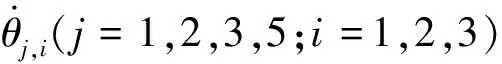
为求机构驱动雅克比矩阵,将3个驱动支链移动副锁定,则可以得到支链i的反螺旋为:
(13)
(14)
另外,式(2)为支链的一个约束反螺旋,同理可以构造出约束雅克比矩阵为
(15)
4 奇异位形分析
根据雅克比矩阵,机构发生奇异的条件可以表示为|J|=0,对雅克比矩阵取行列式有
|J|=|Jav||Jaw|-|Jcv||Jcw|
(16)
(2)|Jaw|=0。令ni=(a1-L1s4,1)×s5,1,则矩阵Jaw中的元素n1、n2、n3在机构中的矢量表示如图4所示。从图4中可以看出,机构在任意位形时都不会出现n1、n2、n3共面的情况,故|Jaw|≠0。因此,机构不会发生此种奇异情况。
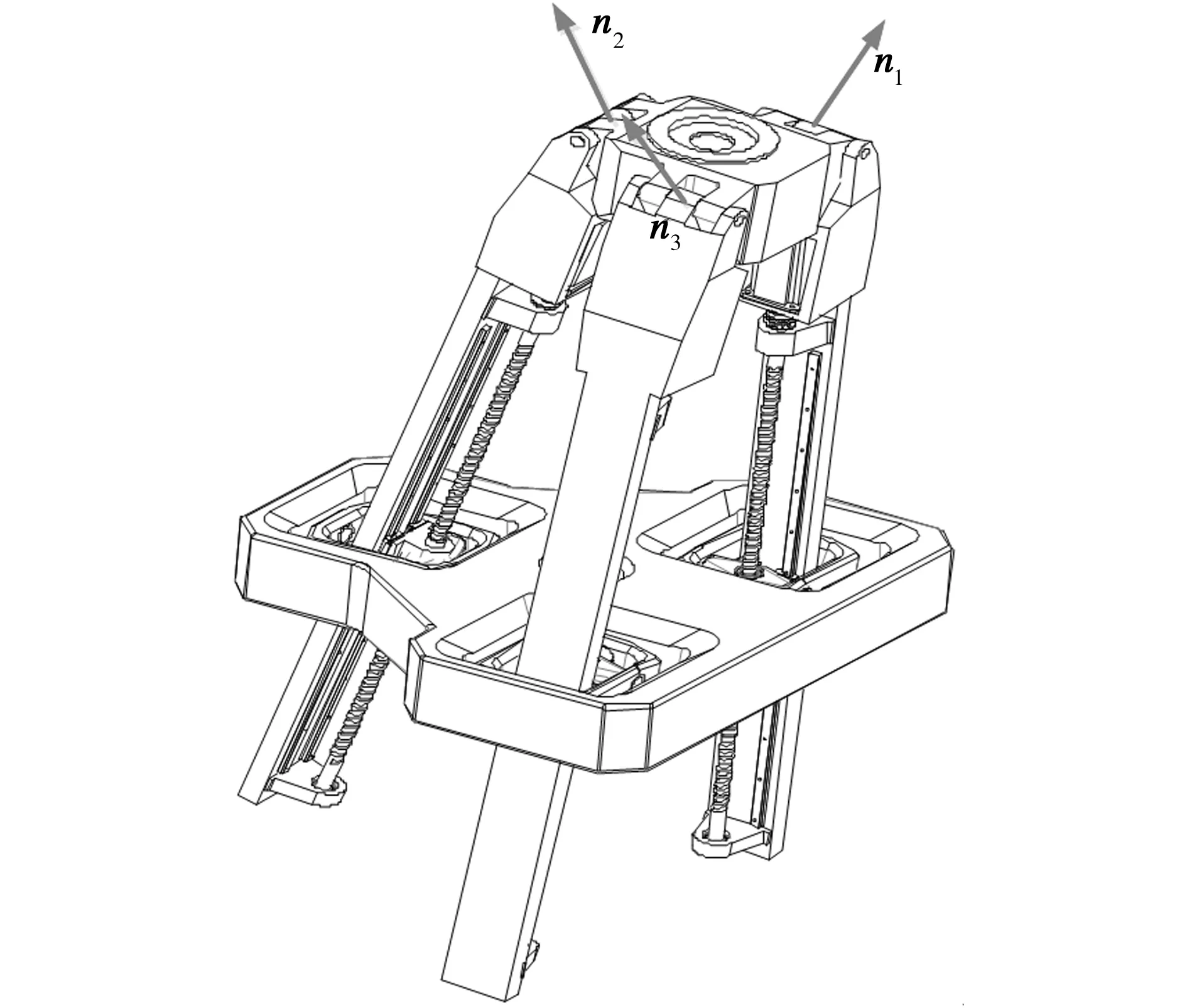
图4 奇异位形
5 运动仿真
(17)
式中:ρ=100 mm;ω=π/180;z0=800 mm;h=20 mm;t=0∶2∶720。
本文采用Matlab与Solidworks Motion运动仿真软件相结合的方法来进行机构平台中心点的运动仿真。首先借助Matlab绘制出三维螺旋线(见图5);然后利用Matlab编制机构位置逆解求解方程,求得并联机构的驱动输入值L1、L2、L3,并将其加载到Solidworks Motion仿真软件中进行运动仿真;最后将仿真出的动平台中心点运动轨迹与Matlab理论轨迹进行比较。
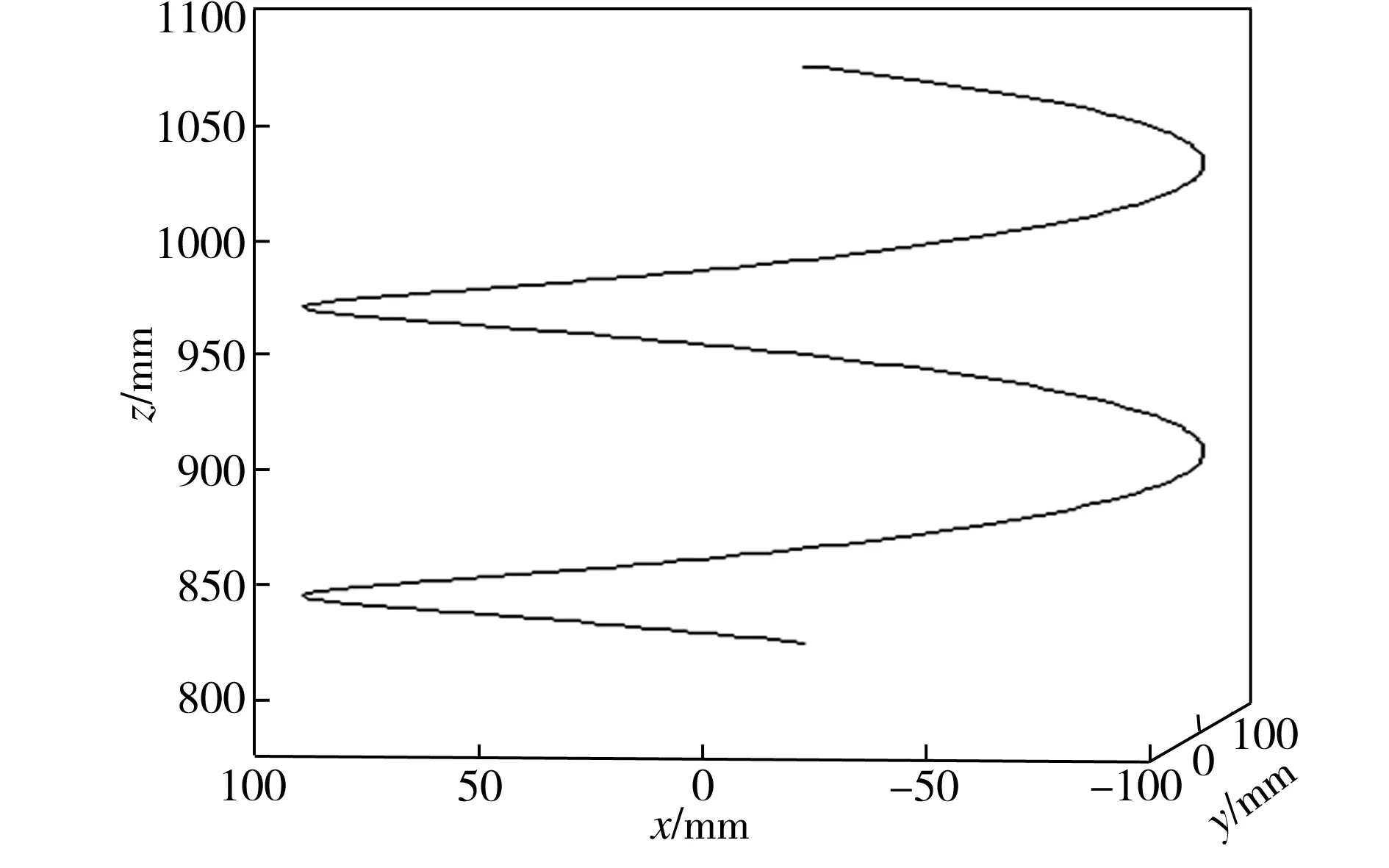
图5 螺旋线
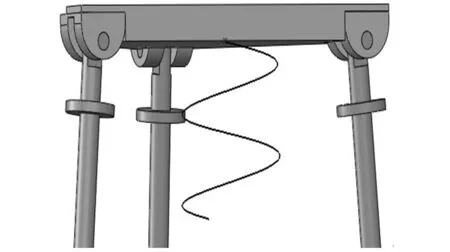
图6 运动轨迹
6 结语
[1] 秦瑞祥,邹冀华. 工业机器人在飞机数字化装配中的应用[J].航空制造技术,2010(23):104-108.
[2] 许国康. 自动钻铆技术及其在飞机数字化装配中的应用[J].航空制造技术,2005(6):45-49.
[3] 许国康. 大型飞机自动化装配技术[J]. 航空学报,2008,29(3):734-740.
[4] De Vlieg R, Feikert E. One-up assembly with robots[J]. SAE International, 2008(1): 22-30.
[5] Summers M. Robot capability test and development of industrial robot positioning system for the aerospace industrial[J].SAE Transactions,2005,114(1):1108-1118.
[6] Bi Shusheng,Liang Jie.Robotic drilling system for titanium structures[J].International Journal of Advanced Manufacturing Technology,2011,54(5-8):767-774.
[7] 陈学生,陈在礼,孔民秀.并联机器人研究的进展与现状[J].机器人,2002,24(5):464-470.
[8] 王友渔,黄田,Chetwynd D G,等. Tricept机械手静刚度解析建模方法[J].机械工程学报,2008,44(8):13-19.
[9] 黄真,孔令富,方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997.
[10]Neumann K E. Robot: US, 4732525[P]. 1986-03-22.
[11]黄真,赵永生,赵铁石. 高等空间机构学[M]. 北京:高等教育出版社,2006.

