利用四能级超导量子干涉仪实现Deutsch算法

程世清，韩丙辰，程鹏

（1.山西大同大学物理与电子科学学院，山西大同037009；2.中建一局集团第三建筑有限公司，北京100161）

0 引言

超导量子干涉仪（SQUID）由于其高灵敏度，易集成等优点广泛应用于量子信息中大规模的量子电路.量子计算机作为量子信息的主要研究方向，它的计算主要由算法决定，不同的算法对应不同的幺正变换.近年来提出利用SQUID与腔场发生共振相互作用和大失谐相互作用实现量子信息的各种方案［1－13］，但它们存在着一些缺点：文献［7－8］中方案要求在门操作过程中调节SQUID的能级间隔；文献［9－10］中方案要求缓慢改变经典场的频率满足绝热条件，按这些要求门的计算速度将变慢；文献［14］中方案中要求两模共振腔，但超导量子比特与多模腔场发生共振相互作用很难.本文中利用四能级超导量子干涉仪与腔场的共振相互作用和大失谐相互作用实现量子计算机的Deutsch算法［1］.此方案有以下优点：1）不需要调节SQUID的能级间隔；2）不需要缓慢的改变经典场的频率满足绝热条件；3）采用单模腔场；4）计算速度快.

1 Deutsch算法

Deutsch算法［1］把量子并行性和量子力学中干涉的性质结合起来，其装置如图1所示.

图1 Deutsch算法的量子电路

输入态｜φ〉0＝｜01〉ab，通过两个Hadamard门后，有，应用Uf到态｜φ〉1上，将出现两种可能的情形：

最后将Hadamard门作用在第一量子比特上得｜φ〉3，如表1所示.

表1 f（x）的函数及相应的幺正变换和函数｜φ〉3

通过测量第一量子比特，可以确定f（0）⊕f（1）的值，此算法只需对f（x）的一次计算即能确定f（x）是常函数还是对称函数.

2 利用四能级SQUIDs实现Deutsch算法

SQUID由约瑟夫森结和超导线圈组成，其哈密顿量可表示为［1］：

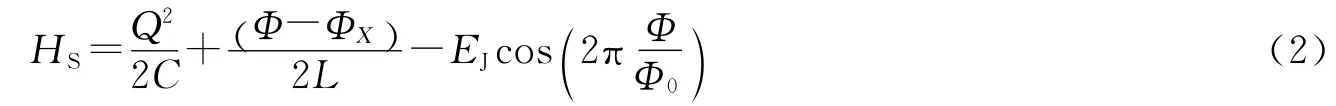
其中Φ为通过线圈的总磁通，Q为结电容上的电荷量，ΦX为外加磁通，为结的能量，Ic为临界电流为磁通量子.

通过设置不同参数，使两SQUIDs有不同的能级间隔.采用四能级SQUIDa，SQUIDb与初始处于单光子态｜1〉c的腔场实现Deutsch算法，如图2所示.

图2 （a）SQUID与腔场的共振相互作用；（b）SQUID与腔场的大失谐相互作用.

2）不同Uf的实现：

A）若f（0）＝f（1）＝0，则Uf为单位矩阵U1，不做任何操作有

B）若f（0）＝f（1）＝1，则Uf为幺正变换U2，其实现过程如下：

C）若f（0）＝0，f（1）＝1，Uf为幺正变换U3，其实现过程如下：

D）若f（0）＝1，f（1）＝0，Uf为幺正变换U4，其实现过程如下：

3）重复1）对SQUIDa的操作，得到不同的｜φ〉3.

4）对SQUIDa做测量，当测得｜φ〉a＝±｜0〉a时，f（x）为常函数，当测得｜φ〉a＝±｜1〉a时，f（x）为对称数，如表1所示.

3 总结

量子计算机较经典计算机有更快的计算速度.Deutsch算法优势在于把量子并行性和量子力学的干涉性质结合起来，它的实现说明量子线路可以超越经典线路.本文中利用四能级超导量子干涉仪与腔场的共振相互作用及大失谐相互作用实现量子计算机的Deutsch算法.此方案较其它方案的优点：不需要调节SQUID的能级间隔，不需要缓慢改变经典场的频率满足绝热条件，采用单模腔场，计算速度快等.

［1］Deutsch D，Jozsa R.Rapid solution of problems by quantum computation［J］.Proc R Soc London A，1992，43339：533－558.

［2］Kis Z，Paspalakis E.Arbitrary rotation and entanglement of squid qubits［J］.Phys Rev B，2004，69：024510－024515.

［3］Yang C P，Han S.Rotation gate for a three－level superconducting quantum［J］.Phys Rev A，2006，74：044302－1—4.

［4］Yang C P，Chu S I，Han S.Time－resolved measurement of computing with superconducting devices：a three－level squid qubit［J］.Phys Rev A，2003，67：042311－1—4.

［5］Yang C P，Han S.N－qubit－controlled phase gate with superconducting qubits［J］.Phys Rev A，2005，72：032311－1—6.

［6］Song K H，Xiang S H，Liu Q，et al.Quantum computation and W－state generation using superconducting flux qubits coupled to a cavity without geometric and dynamical manipulation［J］.Phys Rev A，2007，75：032347－1—5.

［7］Zhang P，Wang Z D，Sun J D，et al.Holonomic quantum computation using superconducting cavity［J］.Phys Rev A，2005，71：042301－1—5.

［8］Yang C P，Chu S I，Han S.Error－prevention scheme with two pairs of qubits［J］.Phys Rev A，2003，70：044303－1—3.

［9］Yang C P，Chu S I，Han S.Simplified realization of two－qubit quantum phase gate with four－level systems in cavity QED［J］.Phys：Condens Matter，2004，16：1907－1911.

［10］Song K H，Zhou W，Guo G C.Quantum logic gate opertation and dentanglement with superconduct［J］.Phys Rev A，2005，71：052310－1—4.

［11］Zheng S B，Guo G C.Generation of schrodinger cat states via the Jaynes－Cummings model with large detuning［J］.Phys Lett A，1996，223：332－336.

［12］Holland M J，Wall D F，Zoller P.Quantum nondemolition observation of quantum jumps by atomic beam deflection［J］.Phys Lett，1991，67：1716－1719.

［13］He X L，Yang C P，Li S，et al，Quantum logical gates with four－level squid coupled to a superconducting resonator［J］.Phys Rev A，2010，82：024301－1—4.

［14］Song K H.Quantum logic gates operation using SQUID qubits in bimodal cavity［J］.China Phys B，2006，15：286－291.